Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУ ВПО
Всероссийский заочный финансово-экономический институт
СТАТИСТИКА
Методические
рекомендации к выполнению статистических
расчётов
курсовых, контрольных и выпускных квалификационных работ
Часть I. Комплексное использование статистических методов
при проведении анализа данных
Для студентов всех специальностей
(первое и второе высшее образование)
«Методические рекомендации к выполнению
статистических расчётов курсовых, контрольных и выпускных квалификационных
работ Часть I. Комплексное использование методов при проведении статистического
анализа данных» разработали:
доктор физико-математических наук, профессор
Кожевникова Г.П.,
кандидат технических наук, доцент Голикова А.В.,
кандидат
экономических наук, профессор. Каманина А.М.,
ст. преподаватель Лысенко
С.Н.,
ст. преподаватель Дмитриева И.А.
Ответственный
редактор Г.П. Кожевникова
«Методические рекомендации к выполнению
статистических расчётов курсовых, контрольных и выпускных квалификационных работ Часть I. Комплексное использование методов при проведении статистического
анализа данных» одобрены на заседании
Научно-методического совета ВЗФЭИ
Проректор, председатель НМС, профессор Д.М. Дайитбегов
Статистика. Методические рекомендации к выполнению
статистических расчётов курсовых, контрольных и выпускных квалификационных работ. Часть I. Комплексное использование методов
при проведении статистического анализа данных. Для студентов всех специальностей (первое и второе высшее
образование). – М.: ВЗФЭИ, 2007. – с.
©
Всероссийский заочный финансово-экономический институт (ВЗФЭИ), 2007
Введение
В процессе изучения курса статистики студенты института всех
специальностей выполняют курсовую работу, составной частью которой является расчетная
часть, имеющая своей целью освоение студентами методики и
технологии проведения статистических расчетов. Студенты специальностей
«Финансы и кредит» и «Бухгалтерский учет, анализ и аудит», обучающиеся по
программе II-го высшего
образования, выполняют по курсу статистики контрольную работу, структура
которой целиком аналогична структуре расчетной части курсовых работ.
Настоящие «Методические рекомендации к выполнению
статистических расчетов» предназначены для использования студентами при решении
задач расчетных заданий курсовых и контрольных работ.
Учебно-методический материал «Рекомендаций» может быть
использован при подготовке студентами выпускных квалификационных работ,
а также в ряде учебных курсов, связанных с применением методов анализа данных.
Структура расчетных заданий курсовых и контрольных работ
основана на использовании методического приема, известного как «сквозная
задача».
Сквозная задача (СЗ) базируется на единой исходной информации
и требует для своего решения последовательного применения комплекса изучаемых
методов, что дает возможность охватить при решении СЗ большую часть
статистической методологии. Преимущество применения такого методического
подхода в курсовых и контрольных работах заключается в отказе от традиционного
для изучения курса статистики решения отдельных, не связанных между собой задач
(иллюстрирующих, в основном, изолированное применение одного из статистических
методов) в пользу освоения студентом последовательных этапов комплексного
статистического исследования.
Содержание сквозной статистической задачи курсовых и
контрольных работ включает в себя:
-
исследование
структуры изучаемой совокупности, в процессе которого осуществляется построение
статистического ряда распределения, его графическое изображение и расчет
различных статических характеристик ряда (Задание 1);
-
выявление наличия и направления корреляционной связи
между изучаемыми признаками путем построения и анализа аналитической
группировки и корреляционной таблицы, а также оценка тесноты связи (Задание 2);
-
применение в решении финансово-экономических задач
метода выборочных наблюдений, расчет ошибок выборки и распространение
полученных результатов на генеральную совокупность (Задание 3).
На примере решения сквозной
статистической задачи студент, по сути, самостоятельно проводит в курсовых и
контрольных работах своего рода мини-исследование, начиная от постановки задачи
и заканчивая экономической интерпретацией статистических характеристик,
полученных в результате проведенных расчетов. Проходя по этапам такого
мини-исследования, студент тем самым постигает суть статистической методологии.
Настоящие учебно-методические
материалы включают два раздела:
I.
Методические рекомендации к выполнению статистических
расчетов.
II.
Образец выполнения Заданий 1-3 курсовых и контрольных
работ.
Раздел I содержит конспективное изложение теоретического
материала в объеме, достаточном для выполнения расчетных заданий, а
также пример, демонстрирующий комплексное применение статистических
методов при поэтапном решении сквозной задачи. Методическими
рекомендациями, изложенными в данном разделе, студенту следует
руководствоваться при выполнении своего варианта расчетных заданий.
Раздел II выполняет двоякую функцию:
-
предоставляет студентам второй демонстрационный
пример выполнения статистических расчетов в соответствии с
методическими рекомендациями I-го
раздела;
-
выступает в качестве наглядного образца,
которым должен руководствоваться студент при оформлении курсовых и
контрольных работах результатов выполнения Заданий 1-3.
Учебно-методический
материал, изложенный в двух разделах, обеспечивает студентов методикой
проведения статистического анализа данных самого разнообразного
социально-экономического характера. Это позволяет студентам использовать данную
методику в изучении различных учебных курсов – демографии, маркетинге,
менеджменте, экономике, финансовом анализе и др.
Для студентов выпускных курсов
учебно-методический материал может быть полезен как руководство к
проведению комплексного статистического анализа данных, исследуемых в
выпускной квалификационной работе.
Раздел I
Методические рекомендации к
выполнению статистических расчётов
Курсовые
и контрольные работы по статистике включают три типовых расчетных
задания.
Задание
1. Исследование
структуры совокупности.
Задание 2. Выявление наличия корреляционной связи между
признаками, установление направления связи и оценка ее тесноты.
Задание 3.
Применение метода выборочных наблюдений.
Методика комплексного
применения статистических методов при выполнении расчетных заданий излагается в
данном разделе с использованием демонстрационного примера.
Демонстрационный пример
При проведении
статистического наблюдения за деятельностью коммерческих банков одного из
регионов РФ за исследуемый период получены выборочные данные об объеме кредитных
вложений и сумме прибыли по 30-ти банкам (выборка 20%-ная, механическая).
В
проводимом статистическом исследовании эти банки выступают как единицы
выборочной совокупности. Генеральную совокупность
образуют все коммерческие банки региона. Анализируемыми признаками
изучаемых единиц совокупности являются Объем
кредитных вложений и Сумма прибыли банка.
Выборочные данные представлены в табл.1.
Таблица 1
Исходные данные
|
Номер
банка
п/п
|
Объем кредитных
вложений,
млн руб.
|
Сумма прибыли,
млн руб.
|
Номер
банка
п/п
|
Объем кредитных
вложений,
млн руб.
|
Сумма прибыли, млн
руб.
|
|
1
|
150,0
|
45,1
|
16
|
167,1
|
58,0
|
|
2
|
40,0
|
6,2
|
17
|
130,0
|
47,0
|
|
3
|
180,0
|
67,0
|
18
|
171,0
|
64,7
|
|
4
|
88,3
|
27,3
|
19
|
148,3
|
46,2
|
|
5
|
170,0
|
62,5
|
20
|
150,0
|
53,7
|
|
6
|
169,0
|
60,0
|
21
|
180,0
|
67,0
|
|
7
|
70,0
|
16,9
|
22
|
198,1
|
68,0
|
|
8
|
112,0
|
20.9
|
23
|
200,0
|
70,0
|
|
9
|
170,0
|
65,0
|
24
|
211,0
|
80,1
|
|
10
|
93,3
|
16,0
|
25
|
190,0
|
67,7
|
|
11
|
136,4
|
69,0
|
26
|
205,0
|
72,0
|
|
12
|
120,0
|
35,0
|
27
|
225,0
|
84,0
|
|
13
|
135,4
|
53,4
|
28
|
230,0
|
87,0
|
|
14
|
173,0
|
66,2
|
29
|
240,0
|
90,2
|
|
15
|
160,0
|
56,0
|
30
|
230,0
|
85,0
|
Задание 1
По исходным
данным (табл.1) необходимо выполнить следующее:
1.
Построить статистический ряд распределения банков по Объему
кредитных вложений, образовав четыре группы с равными
интервалами.
2.
Графическим методом и путем расчётов определить
значения моды и медианы полученного ряда распределения.
3.
Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислить среднюю
арифметическую по исходным данным (табл. 1.1), сравнить её с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения.
Объяснить причину их расхождения.
Сделать
выводы по результатам выполнения Задания 1.
Выполнение Задания 1
Целью выполнения
данного Задания
является изучение состава и структуры выборочной совокупности банков путем
построения и анализа статистического ряда распределения банков по признаку Объем кредитных вложений.
1.Построение
интервального ряда распределения банков по объему кредитных вложений
Для построения
интервального вариационного ряда, характеризующего распределение банков по
объему кредитных вложений, необходимо вычислить величину и границы
интервалов ряда.
При построении ряда с
равными интервалами величина интервала h определяется по формуле
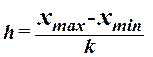 , (1)
, (1)
где 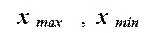 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
Число групп k задается в условии задания или
рассчитывается по формуле Г.Стерджесса
k=1+3,322 lg n,
(2)
где n - число
единиц совокупности.
Определение
величины интервала по формуле (1) при заданных k = 4, xmax
= 240 млн руб., xmin = 40 млн
руб.:
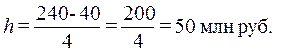
При h = 50 млн руб. границы
интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица
2
|
Номер группы
|
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
|
1
|
40
|
90
|
|
2
|
90
|
140
|
|
3
|
140
|
190
|
|
4
|
190
|
240
|
Для
построения интервального ряда необходимо подсчитать число банков, входящих в
каждую группу (частоты групп). При этом возникает вопрос, в какую группу
включать единицы совокупности, у которых значения признака выступают
одновременно и верхней, и нижней границами смежных интервалов (для
демонстрационного примера – это 90, 140, 190 млн руб.). Отнесение таких единиц
к одной из двух смежных групп рекомендуется осуществлять по принципу
полуоткрытого интервала [ ).
Т.к. при этом верхние границы интервалов не принадлежат данным интервалам, то
соответствующие им единицы совокупности включаются не в данную группу, а в
следующую. В последний интервал включаются и нижняя, и верхняя
границы.
Процесс группировки
единиц совокупности по признаку Объем кредитных вложений представлен во вспомогательной (разработочной) таблице 3
(графа 4 этой таблицы необходима для построения аналитической группировки в
Задании 2).
Таблица 3
Разработочная таблица для построения интервального
ряда распределения и аналитической группировки
|
Группы банков по
объему кредитных вложений, млн руб.
|
Номер банка
|
Объем кредитных
вложений, млн руб.
|
Сумма прибыли,
млн руб.
|
|
1
|
2
|
3
|
4
|
|
40 – 90
|
2
|
40,0
|
6,2
|
|
|
7
|
70,0
|
16,9
|
|
|
4
|
88,3
|
27,3
|
|
Всего
|
3
|
198,3
|
50,4
|
|
90 – 140
|
10
|
93,3
|
16,0
|
|
|
8
|
112,0
|
20,9
|
|
|
12
|
120,0
|
35,0
|
|
|
17
|
130,0
|
47,0
|
|
|
13
|
135,4
|
53,4
|
|
|
11
|
136,4
|
69,0
|
|
Всего
|
6
|
727,1
|
241,3
|
|
140 – 190
|
19
|
148,3
|
46,2
|
|
|
1
|
150,0
|
45,1
|
|
|
20
|
150,0
|
53,7
|
|
|
15
|
160,0
|
56,0
|
|
|
16
|
167,1
|
58,0
|
|
|
6
|
169,0
|
60,0
|
|
|
5
|
170,0
|
62,5
|
|
|
9
|
170,0
|
65,0
|
|
|
18
|
171,0
|
64,7
|
|
|
14
|
173,0
|
66,2
|
|
|
3
|
180,0
|
67,0
|
|
|
21
|
180,0
|
67,0
|
|
Всего
|
12
|
1988,4
|
711,4
|
|
191 – 240
|
25
|
190,0
|
67,7
|
|
|
22
|
198,1
|
68,0
|
|
|
23
|
200,0
|
70,0
|
|
|
26
|
205,0
|
72,0
|
|
|
24
|
211,0
|
80,1
|
|
|
27
|
225,0
|
84,0
|
|
|
28
|
230,0
|
87,0
|
|
|
30
|
230,0
|
85,0
|
|
|
29
|
240,0
|
90,2
|
|
Всего
|
9
|
1929,1
|
704,0
|
|
ИТОГО
|
30
|
4842,9
|
1707,1
|
На основе групповых
итоговых строк «Всего» табл. 3 формируется итоговая таблица 4, представляющая интервальный
ряд распределения банков по объему кредитных вложений.
Таблица 4
Распределение банков по объему кредитных вложений
|
Номер группы
|
Группы банков по объему кредитных вложений,
млн руб.,
х
|
Число банков,
f
|
|
1
|
40 – 90
|
3
|
|
2
|
90 – 140
|
6
|
|
3
|
140 – 190
|
12
|
|
4
|
190 – 240
|
9
|
|
|
Итого
|
30
|
Помимо частот
групп в абсолютном выражении в анализе интервальных рядов используются ещё три
характеристики ряда, приведенные в графах 4 - 6 табл. 1.4. Это частоты групп в относительном выражении,
накопленные (кумулятивные) частоты Sj, получаемые путем последовательного
суммирования частот всех предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле 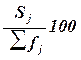 .
.
Таблица 5
Структура банков по объему кредитных вложений
|
№ группы
|
Группы банков по объему кредитных вложений,
млн руб.
|
Число банков, fj
|
Накопленная
частота,
Sj
|
Накопленная
частоcть, %
|
|
в абсолютном выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
40 – 90
|
3
|
10,0
|
3
|
10,0
|
|
2
|
90 – 140
|
6
|
20,0
|
9
|
30,0
|
|
3
|
140 – 190
|
12
|
40,0
|
21
|
70,0
|
|
4
|
190 – 240
|
9
|
30,0
|
30
|
100,0
|
|
|
Итого
|
30
|
100,0
|
|
|
Вывод. Анализ интервального ряда
распределения изучаемой совокупности банков показывает, что распределение
банков по объему кредитных вложений не является равномерным: преобладают банки
с кредитными вложениями от 140 млн руб. до 190 млн руб. (это 12 банков, доля
которых составляет 40%); 30% банков имеют кредитные вложения менее 140 млн
руб., а 70% – менее 190 млн руб.
1.2. Нахождение моды и медианы
полученного интервального ряда распределения графическим методом и путем расчетов
Мода и медиана являются структурными
средними величинами, характеризующими (наряду со средней
арифметической) центр распределения единиц совокупности по изучаемому признаку.
Мода Мо для дискретного ряда – это значение признака, наиболее
часто встречающееся у единиц исследуемой совокупности[1]. В
интервальном вариационном ряду модой приближенно считается центральное значение модального
интервала (имеющего наибольшую частоту). Более точно моду можно
определить графическим методом по гистограмме ряда (рис.1).
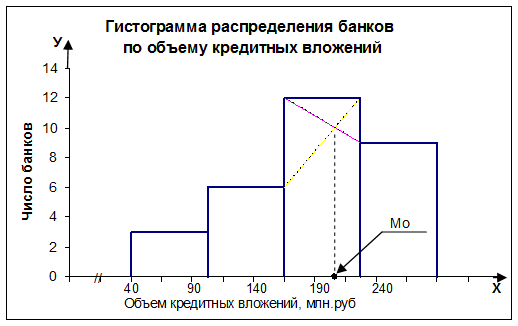
Рис. 1
Определение моды графическим методом
Конкретное значение моды для интервального ряда
рассчитывается по формуле:
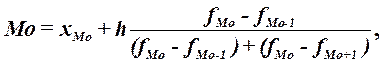 (3)
(3)
где хМo – нижняя
граница модального интервала,
h –величина
модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным.
Согласно табл.1.3
модальным интервалом построенного ряда является интервал 140 – 190 млн. руб.,
так как его частота максимальна (f3 = 12).
Расчет моды по формуле
(3):
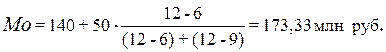
Вывод. Для рассматриваемой совокупности банков наиболее распространенный объем
кредитных вложений характеризуется средней величиной 173,33 млн руб.
Медиана Ме – это значение признака,
приходящееся на середину ранжированного ряда. По обе стороны от медианы
находится одинаковое количество единиц совокупности.
Медиану можно определить
графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по
накопленным частотам (табл. 5, графа 5).
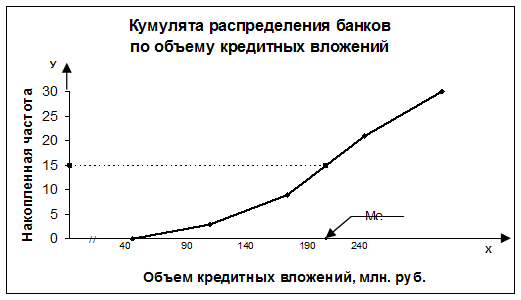
Рис. 2.
Определение медианы графическим методом
Конкретное значение
медианы для интервального ряда рассчитывается по формуле:
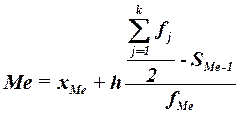 ,
(4)
,
(4)
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
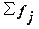 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Для расчета медианы
необходимо, прежде всего, определить медианный интервал, для чего используются
накопленные частоты (или частости) из табл. 5 (графа 5). Так как медиана делит
численность ряда пополам, она будет располагаться в том интервале, где накопленная
частота впервые равна полусумме всех частот 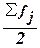 или превышает ее (т.е. все предшествующие накопленные частоты
меньше этой величины).
или превышает ее (т.е. все предшествующие накопленные частоты
меньше этой величины).
В демонстрационном
примере медианным интервалом является интервал 140 – 190 млн. руб., так как именно в этом
интервале накопленная частота Sj = 21 впервые превышает величину,
равную половине численности единиц совокупности (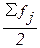 =
=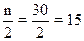 ).
).
Расчет значения медианы
по формуле (4):
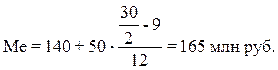
Вывод. В рассматриваемой совокупности
банков половина банков имеют в среднем объем кредитных вложений не более 165
млн руб., а другая половина – не менее 165 млн руб.
3. Расчет характеристик ряда
распределения
Для расчета характеристик
ряда распределения 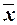 , σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (
, σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (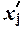 – середина j-го интервала).
– середина j-го интервала).
Таблица 6
Расчетная таблица для нахождения характеристик ряда
распределения
|
Группы банков по объему кредитных вложений,
млн руб.
|
Середина интервала,
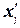
|
Число банков,
fj
|
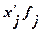
|
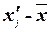
|
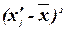
|
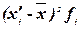
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
40 – 90
|
65
|
3
|
195
|
-95
|
9025
|
27075
|
|
90 – 140
|
115
|
6
|
690
|
-45
|
2025
|
12150
|
|
140 – 190
|
165
|
12
|
1980
|
5
|
25
|
300
|
|
190 – 240
|
215
|
9
|
1935
|
55
|
3025
|
27225
|
|
Итого
|
|
30
|
4800
|
|
|
66750
|
Расчет средней
арифметической взвешенной:
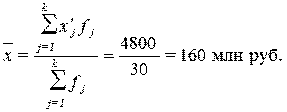 (5)
(5)
Расчет среднего квадратического
отклонения:
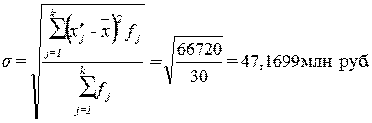 (6)
(6)
Расчет дисперсии:
σ2 =47,16992=2225,00
Расчет коэффициента вариации:
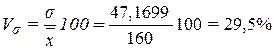 (7)
(7)
Вывод. Анализ полученных значений показателей 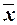 и σ говорит о том, что средний объем
кредитных вложений банков составляет 165 млн руб., отклонение от среднего
объема в ту или иную сторону составляет в среднем 47,17 млн руб. (или 29,5%),
наиболее характерные значения объема кредитных вложений находятся в пределах от
112,83 млн руб. до 207,17 млн руб. (диапазон
и σ говорит о том, что средний объем
кредитных вложений банков составляет 165 млн руб., отклонение от среднего
объема в ту или иную сторону составляет в среднем 47,17 млн руб. (или 29,5%),
наиболее характерные значения объема кредитных вложений находятся в пределах от
112,83 млн руб. до 207,17 млн руб. (диапазон 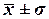 ).
).
Значение Vσ = 29,5% не превышает 33%, следовательно, вариация кредитных
вложений в исследуемой совокупности банков незначительна и совокупность по
данному признаку качественно однородна. Расхождение между значениями 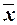 , Мо и Ме незначительно (
, Мо и Ме незначительно (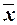 =160млн руб., Мо=173,33млн
руб., Ме=165млн руб.), что
подтверждает вывод об однородности совокупности банков. Таким образом,
найденное среднее значение объема кредитных вложений банков (160 млн руб.)
является типичной, надежной характеристикой исследуемой совокупности банков.
=160млн руб., Мо=173,33млн
руб., Ме=165млн руб.), что
подтверждает вывод об однородности совокупности банков. Таким образом,
найденное среднее значение объема кредитных вложений банков (160 млн руб.)
является типичной, надежной характеристикой исследуемой совокупности банков.
4.Вычисление средней арифметической
по исходным данным
Для расчета применяется
формула средней арифметической простой:
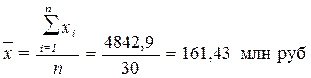 , (8)
, (8)
Причина расхождения
средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по
формуле (8) средняя определяется по фактическим
значениям исследуемого признака
для всех 30-ти банков, а по формуле (5) средняя
вычисляется для интервального ряда, когда в качестве значений признака берутся
середины интервалов 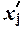 и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
Задание 2
По исходным данным табл. 1 с использованием результатов выполнения
Задания 1 необходимо выполнить следующее:
1.
Установить наличие и характер корреляционной связи
между признаками Объем кредитных вложений и Сумма прибыли,
образовав по каждому признаку четыре группы с равными интервалами, используя
методы:
а)
аналитической группировки;
б)
корреляционной таблицы.
2.
Оценить тесноту корреляционной связи, используя
коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать
выводы по результатам выполнения Задания 2.
Выполнение Задания 2
Целью выполнения
данного Задания
является выявление наличия корреляционной связи между факторным и
результативным признаками,
установление направления связи и оценка ее тесноты.
Факторный и результативный признаки
либо задаются в условии задания, либо определяются путем проведения
предварительного теоретического анализа. Лишь после того, как выяснена
экономическая сущность явления и определены факторный и результативный
признаки, приступают к проведению корреляционного анализа данных.
По условию Задания 2 факторным
является признак Объем кредитных вложений (X), результативным –
признак Сумма прибыли (Y).
1. Установление наличия и характера связи между признаками Объем кредитных вложений и Сумма прибыли методами аналитической
группировки и корреляционной таблицы
1а. Применение метода
аналитической группировки
При использовании метода
аналитической группировки строится интервальный ряд распределения единиц
совокупности по факторному признаку Х
и для каждой j-ой группы
ряда определяется среднегрупповое значение 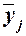 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 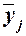 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя разработочную таблицу 3,
строим аналитическую группировку, характеризующую зависимость между факторным
признаком Х – Объем кредитных вложений и
результативным признаком Y – Сумма
прибыли. Макет аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7
Зависимость суммы
прибыли банков от объема кредитных вложений
|
Номер группы
|
Группы банков по объему кредитных вложений,
млн руб.
|
Число банков
|
Сумма прибыли,
млн руб.
|
|
всего
|
в среднем на один банк
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
Итого
|
|
|
|
|
Групповые средние значения 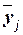 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8.
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8.
Таблица 8
Зависимость суммы прибыли банков от объема кредитных
вложений
|
Номер группы
|
Группы банков по объему кредитных вложений,
млн руб.,
х
|
Число банков,
fj
|
Сумма прибыли,
млн руб.
|
|
всего
|
в среднем на один банк,
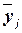
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
40 – 90
|
3
|
50,4
|
16,800
|
|
2
|
90 – 140
|
6
|
241,3
|
40,217
|
|
3
|
140 – 190
|
12
|
711,4
|
59,283
|
|
4
|
190 – 240
|
9
|
704,0
|
78,222
|
|
|
Итого
|
30
|
1707,1
|
56,90
|
Вывод. Анализ
данных табл. 8 показывает, что с увеличением объема кредитных вложений от
группы к группе систематически возрастает и средняя прибыль по каждой группе
банков, что свидетельствует о наличии прямой корреляционной связи между
исследуемыми признаками.
1б. Применение метода
корреляционной таблицы.
Корреляционная таблица
представляет собой комбинацию двух рядов распределения. Строки таблицы
соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по
результативному признаку Y. На пересечении j-ой строки и k-ой графы указывается число единиц
совокупности, входящих в j-ый интервал по факторному признаку и
в k-ый интервал
по результативному признаку. Концентрация частот около диагонали
построенной таблицы свидетельствует о наличии корреляционной связи между
признаками. Связь прямая, если частоты располагаются по диагонали, идущей от
левого верхнего угла к правому нижнему. Расположение частот по диагонали от
правого верхнего угла к левому нижнему говорит об обратной связи.
Для построения
корреляционной таблицы необходимо знать величины и границы интервалов по двум
признакам X и Y. Величина интервала и границы интервалов для
факторного признака Х
– Объем кредитных вложений известны
из табл. 8. Для результативного признака Y
– Сумма прибыли величина интервала
определяется по формуле (1) при k = 4, уmax = 90,2 млн руб., уmin = 6,2 млн руб.:
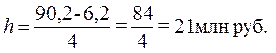
Границы интервалов ряда распределения
результативного признака Y имеют следующий вид (табл. 9):
Таблица 9
|
Номер группы
|
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
|
1
|
6,2
|
27,2
|
|
2
|
27,2
|
48,2
|
|
3
|
48,2
|
69,2
|
|
4
|
69,2
|
90,2
|
Подсчитывая с
использованием принципа полуоткрытого интервала [ ) число банков, входящих в каждую
группу (частоты групп), получаем интервальный ряд распределения
результативного признака (табл. 10).
Таблица 10
Распределение банков по сумме прибыли
|
Группы банков по сумме прибыли, млн. руб.,
х
|
Число банков,
fj
|
|
6,2 – 27,2
|
4
|
|
27,2 – 48,2
|
5
|
|
48,2 – 69,2
|
14
|
|
69,2 – 90,2
|
7
|
|
Итого
|
30
|
Используя
группировки по факторному и результативному признакам, строим корреляционную
таблицу (табл. 11).
Таблица 11
Корреляционная таблица зависимости суммы прибыли
банков
от объема кредитных вложений
|
Группы банков по размеру кредитных
вложений,
млн руб.
|
Группы банков по сумме прибыли, млн руб.
|
|
|
6,2 – 27,2
|
27,2 – 48,2
|
48,2 – 69,2
|
69,2 – 90,2
|
Итого
|
|
40 – 90
|
2
|
1
|
|
|
3
|
|
90 – 140
|
2
|
2
|
2
|
|
6
|
|
140 – 190
|
|
2
|
10
|
0
|
12
|
|
190 – 240
|
|
|
2
|
7
|
9
|
|
Итого
|
5
|
5
|
5
|
15
|
30
|
Вывод. Анализ данных табл. 11 показывает,
что распределение частот групп произошло вдоль диагонали, идущей из левого
верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии
прямой корреляционной связи между объемом кредитных вложений и суммой прибыли
банков.
2. Измерение тесноты
корреляционной связи с использованием коэффициента детерминации и эмпирического
корреляционного отношения
Для измерения тесноты
связи между факторным и результативным признаками рассчитывают специальные
показатели – эмпирический коэффициент детерминации 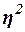 и эмпирическое
корреляционное отношение
и эмпирическое
корреляционное отношение 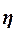 .
.
Эмпирический коэффициент детерминации 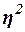 оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель
оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель 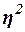 рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
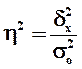 , (9)
, (9)
где 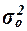 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
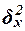 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Значения показателя 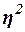 изменяются в пределах
изменяются в пределах
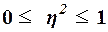 . При отсутствии корреляционной связи
между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи
между признаками Х и Y имеет место равенство 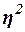 =0, а при наличии функциональной связи
между ними - равенство
=0, а при наличии функциональной связи
между ними - равенство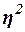 =1.
=1.
Общая дисперсия
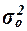 характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
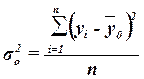 ,
(10)
,
(10)
где yi –
индивидуальные значения результативного признака;
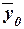 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц совокупности.
Общая
средняя 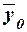 вычисляется как средняя арифметическая простая
по всем единицам совокупности:
вычисляется как средняя арифметическая простая
по всем единицам совокупности:
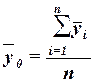 (11)
(11)
или как средняя
взвешенная по частоте групп интервального ряда:
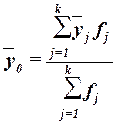 (12)
(12)
Для
вычисления 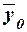 удобно использовать
формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения
числителя и знаменателя формулы.
удобно использовать
формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения
числителя и знаменателя формулы.
Расчет
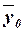 по формуле (11):
по формуле (11):
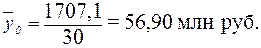
Для расчета общей
дисперсии 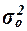 применяется вспомогательная таблица
12.
применяется вспомогательная таблица
12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
|
Номер
банка
п/п
|
Прибыль, млн руб.
|
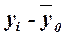
|
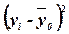
|
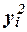
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
45,1
|
-11,803
|
139,3187
|
2034,01
|
|
2
|
6,2
|
-50,703
|
2570,8280
|
38,44
|
|
3
|
67,0
|
10,097
|
101,9427
|
4489,00
|
|
4
|
27,3
|
-29,603
|
876,3573
|
745,29
|
|
5
|
62,5
|
5,597
|
31,3227
|
3906,25
|
|
6
|
60,0
|
3,097
|
9,5893
|
3600,00
|
|
7
|
16,9
|
-40,003
|
1600,2667
|
285,61
|
|
8
|
20,9
|
-36,003
|
1296,2400
|
436,81
|
|
9
|
65,0
|
8,097
|
65,5560
|
4225,00
|
|
10
|
16,0
|
-40,903
|
1673,0827
|
256,00
|
|
11
|
69,0
|
12,097
|
146,3293
|
4761,00
|
|
12
|
35,0
|
-21,903
|
479,7560
|
1225,00
|
|
13
|
53,4
|
-3,503
|
12,2733
|
2851,56
|
|
14
|
66,2
|
9,297
|
86,4280
|
4382,44
|
|
15
|
56,0
|
-0,903
|
0,8160
|
3136,00
|
|
16
|
58,0
|
1,097
|
1,2027
|
3364,00
|
|
17
|
47,0
|
-9,903
|
98,0760
|
2209,00
|
|
18
|
64,7
|
7,797
|
60,7880
|
4186,09
|
|
19
|
46,2
|
-10,703
|
114,5613
|
2134,44
|
|
20
|
53,7
|
-3,203
|
10,2613
|
2883,69
|
|
21
|
67,0
|
10,097
|
101,9427
|
4489,00
|
|
22
|
68,0
|
11,097
|
123,1360
|
4624,00
|
|
23
|
70,0
|
13,097
|
171,5227
|
4900,00
|
|
24
|
80,1
|
23,197
|
538,0853
|
6416,01
|
|
25
|
67,7
|
10,797
|
116,5680
|
4583,29
|
|
26
|
72,0
|
15,097
|
227,9093
|
5184,00
|
|
27
|
84,0
|
27,097
|
734,2293
|
7056,00
|
|
28
|
87,0
|
30,097
|
905,8093
|
7569,00
|
|
29
|
90,2
|
33,297
|
1108,6680
|
8136,04
|
|
30
|
85,0
|
28,097
|
789,4227
|
7225,00
|
|
Итого
|
1707,1
|
1650,197
|
14192,2897
|
111331,97
|
Расчет общей
дисперсии по формуле
(10):
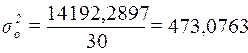
Общая дисперсия может
быть также рассчитана по формуле
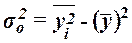 ,
,
где  – средняя из квадратов значений
результативного признака,
– средняя из квадратов значений
результативного признака,
 – квадрат средней величины значений
результативного признака.
– квадрат средней величины значений
результативного признака.
Для
демонстрационного примера
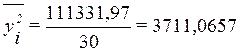
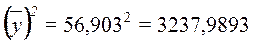
Тогда
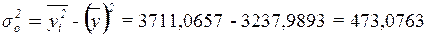
Межгрупповая
дисперсия 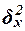 измеряет
систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена
группировка). Воздействие фактора Х
на результативный признак Y проявляется в отклонении
групповых средних
измеряет
систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена
группировка). Воздействие фактора Х
на результативный признак Y проявляется в отклонении
групповых средних 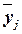 от
общей средней
от
общей средней 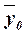 . Показатель
. Показатель 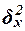 вычисляется по формуле
вычисляется по формуле
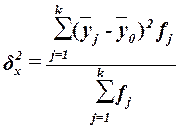 , (13)
, (13)
где 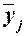 –групповые
средние,
–групповые
средние,
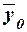 –
общая средняя,
–
общая средняя,
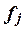 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета
межгрупповой дисперсии 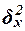 строится вспомогательная таблица 13 При этом
используются групповые средние значения
строится вспомогательная таблица 13 При этом
используются групповые средние значения 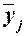 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой
дисперсии
|
Группы банков по размеру кредитных
вложений,
млн руб.
|
Число банков,

|
Среднее значение 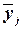 в группе в группе
|
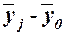
|
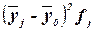
|
|
1
|
2
|
3
|
4
|
5
|
|
40 –
90
|
3
|
16,800
|
-40,103
|
4824,8320
|
|
90 –
140
|
6
|
40,216
|
-16,687
|
1670,6690
|
|
140 – 190
|
12
|
59,283
|
2,380
|
67,9728
|
|
190 – 240
|
9
|
78,222
|
21,319
|
4090,4552
|
|
Итого
|
30
|
|
|
10653,9291
|
Расчет межгрупповой дисперсии 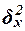 по формуле (11):
по формуле (11):
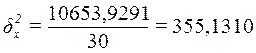
Расчет
эмпирического коэффициента детерминации 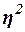 по формуле (9):
по формуле (9):
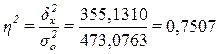 или 75,1%
или 75,1%
Вывод. 75,1% вариации суммы прибыли банков
обусловлено вариацией объема кредитных вложений, а 24,9% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное
отношение 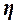 оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
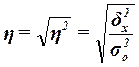 (14)
(14)
Значение показателя изменяются в пределах 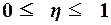 . Чем ближе значение
. Чем ближе значение 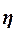 к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе 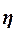 служит шкала Чэддока (табл. 14):
служит шкала Чэддока (табл. 14):
Таблица
14
Шкала Чэддока
|
h
|
0,1 – 0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Характеристика
силы связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма тесная
|
Расчет эмпирического корреляционного
отношения 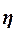 по формуле (14):
по формуле (14):
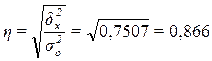 или 86,6%
или 86,6%
Вывод. Согласно шкале Чэддока связь между
объемом кредитных вложений и суммой
прибыли банков является тесной.
Задание 3
По
результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1)
ошибку выборки средней величины объема кредитных
вложений банков и границы, в которых будет находиться генеральная средняя.
2)
ошибку
выборки доли банков
с объемом кредитных
вложений 175 млн руб. и выше, а
также границы, в которых будет находиться генеральная доля.
3)
необходимый объем выборки при заданной предельной
ошибке выборки, равной 10 млн руб.
Выполнение Задания 3
Целью выполнения
данного Задания
является определение для генеральной совокупности коммерческих банков региона
границ, в которых будут находиться величина среднего объема кредитных вложений
банков и доля банков с объемом кредитных вложений не менее 175 млн руб.
1.
Определение ошибки выборки для среднего объема кредитных вложений банков и
границ, в которых будет находиться генеральная средняя
Применение выборочного
метода наблюдения всегда связано с установлением степени достоверности оценок
показателей генеральной совокупности, полученных на основе значений
показателей выборочной совокупности. Достоверность этих оценок зависит от
репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические
свойства генеральной совокупности. Как
правило, генеральные и выборочные характеристики не совпадают, а отклоняются на
некоторую величину ε, которую называют ошибкой
выборки (ошибкой репрезентативности).
Значения признаков
единиц, отобранных из генеральной совокупности в выборочную, всегда случайны,
поэтому и статистические характеристики выборки случайны, следовательно, и
ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок -
среднюю 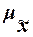 и предельную
и предельную 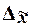 .
.
Средняя ошибка
выборки 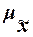 - это среднее
квадратическое отклонение всех возможных значений выборочной средней от
генеральной средней, т.е. от своего математического ожидания M[
- это среднее
квадратическое отклонение всех возможных значений выборочной средней от
генеральной средней, т.е. от своего математического ожидания M[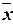 ].
].
Величина
средней ошибки выборки рассчитывается дифференцированно
(по различным формулам) в зависимости от вида
и способа отбора единиц из генеральной совокупности в выборочную.
Для
собственно-случайной и механической выборки с бесповторным способом отбора
средняя ошибка 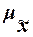 выборочной средней
выборочной средней 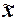 определяется по формуле
определяется по формуле
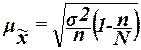 ,
(15)
,
(15)
где 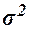 – общая дисперсия выборочных значений
признаков,
– общая дисперсия выборочных значений
признаков,
N – число единиц в генеральной
совокупности,
n – число единиц в выборочной
совокупности.
Предельная ошибка выборки 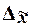 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
 ,
,
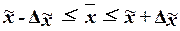 ,
(16)
,
(16)
где 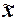 – выборочная средняя,
– выборочная средняя,
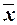 – генеральная средняя.
– генеральная средняя.
Границы задают доверительный
интервал генеральной средней, т.е. случайную область значений, которая
с вероятностью Р гарантированно содержит значение генеральной средней.
Эту вероятность Р называют доверительной
вероятностью или уровнем
надёжности.
В экономических
исследованиях чаще всего используются доверительные вероятности Р= 0.954, Р=
0.997, реже Р= 0,683.
В математической
статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке µ с коэффициентом кратности t (называемым также коэффициентом доверия), который зависит от значения
доверительной вероятности Р. Для
предельной ошибки выборочной средней 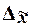 это теоретическое
положение выражается формулой
это теоретическое
положение выражается формулой
 (17)
(17)
Значения t вычислены заранее для различных
доверительных вероятностей Р и протабулированы (таблицы
функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р
значения t
задаются следующим образом (табл. 15):
Таблица 15
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию
демонстрационного примера выборочная совокупность насчитывает 30 банков,
выборка 20% механическая, следовательно, генеральная совокупность включает 150
банков. Выборочная средняя 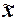 , дисперсия
, дисперсия 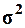 определены в Задании 1 (п. 3).
Значения параметров, необходимых для решения задачи, представлены в табл. 16:
определены в Задании 1 (п. 3).
Значения параметров, необходимых для решения задачи, представлены в табл. 16:
Таблица 16
|
Р
|
t
|
n
|
N
|
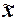
|

|
|
0,954
|
2
|
30
|
150
|
160
|
2225
|
Расчет
средней ошибки выборки по формуле (15):
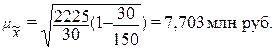 ,
,
Расчет предельной ошибки
выборки по формуле (17):

Определение по формуле
(16) доверительного интервала для генеральной средней:
160-15,406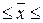 160+15,406,
160+15,406,
144,594 млн руб. 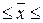 175,406 млн руб.
175,406 млн руб.
Вывод. На основании проведенного
выборочного обследования коммерческих банков региона с вероятностью 0,954 можно
утверждать, что для генеральной совокупности банков средний объем кредитных
вложений банка находится в пределах от 144,59 млн руб. до 175,41 млн руб.
2. Определение ошибки выборки для доли
банков с объемом кредитных вложений 175млн руб. и выше, а также границ, в
которых будет находиться генеральная доля
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
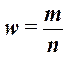 ,
(18)
,
(18)
где
m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 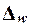 доли единиц, обладающих заданным свойством,
рассчитывается по формуле
доли единиц, обладающих заданным свойством,
рассчитывается по формуле
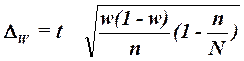 , (19)
, (19)
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная
ошибка выборки 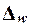 определяет границы, в пределах которых будет
находиться генеральная доля р единиц, обладающих заданным
свойством:
определяет границы, в пределах которых будет
находиться генеральная доля р единиц, обладающих заданным
свойством:
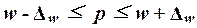 (20)
(20)
По условию Задания 3
исследуемым свойством является равенство
или превышение объема кредитных вложений банка величины 175 млн руб.
Число банков с
заданным свойством определяется из табл. 3 (графа 3):
m=11
Расчет
выборочной доли по формуле (18):
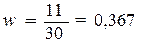
Расчет по формуле (19)
предельной ошибки выборки для доли:
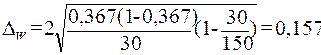
Определение по формуле
(20) доверительного интервала генеральной доли:

0,21 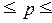 0,524
0,524
или
21% 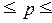 52,4%
52,4%
Вывод. С вероятностью
0,954 можно утверждать, что в генеральной совокупности банков доля банков
с объемом кредитных вложений 175 млн руб. и выше будет находиться в пределах от
21% до 52,4%.
3. Определение
необходимого объема выборки с заданным значением допустимой предельной ошибки
выборки, равной 10 млн руб.
Для собственно-случайной и механической выборки с бесповторным способом
отбора необходимый объем выборки для средней количественного признака
вычисляется по формуле
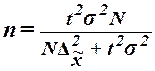 (21)
(21)
По условию демонстрационного примера ошибка выборки 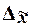 не должна превышать 10 млн руб. Параметры t, N и
не должна превышать 10 млн руб. Параметры t, N и 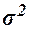 известны из решений предыдущих задач.
известны из решений предыдущих задач.
Расчет необходимой численности выборки по формуле (21):
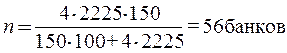
Вывод. Для
того, чтобы обеспечить для среднего объема кредитных вложений банков предельную
ошибку выборки, равную 10 млн руб., необходимо из 150 банков, составляющих
генеральную совокупность, отобрать в выборочную совокупность 56 банков.
Раздел II
Образец
выполнения и оформления
Заданий 1-3 курсовых
и контрольных работ
Имеются следующие выборочные
данные по 30-ти однотипным фирмам одного из регионов РФ, характеризующие
деятельность фирм за исследуемый период (выборка 10%-ная механическая):
Таблица 1
Исходные данные
|
Номер
фирмы
п/п
|
Среднесписочная
численность
менеджеров,
чел.
|
Объём
продаж,
млн
руб.
|
Номер
фирмы
п/п
|
Среднесписочная
численность
менеджеров,
чел.
|
Объём
продаж,
млн
руб.
|
|
1
|
35
|
3,30
|
16
|
50
|
4,00
|
|
2
|
26
|
2,80
|
17
|
31
|
3,00
|
|
3
|
20
|
2,50
|
18
|
33
|
3,30
|
|
4
|
24
|
2,60
|
19
|
41
|
3,50
|
|
5
|
30
|
3,00
|
20
|
31
|
3,00
|
|
6
|
33
|
3,10
|
21
|
36
|
3,35
|
|
7
|
28
|
2,90
|
22
|
36
|
3,45
|
|
8
|
35
|
3,40
|
23
|
37
|
3,47
|
|
9
|
42
|
3,60
|
24
|
37
|
3,50
|
|
10
|
27
|
2,90
|
25
|
38
|
3,60
|
|
11
|
36
|
3,30
|
26
|
39
|
3,70
|
|
12
|
22
|
2,60
|
27
|
43
|
3,60
|
|
13
|
25
|
2,80
|
28
|
44
|
4,00
|
|
14
|
35
|
3,35
|
29
|
46
|
3,90
|
|
15
|
32
|
3,10
|
30
|
48
|
3,80
|
Цель статистического исследования - анализ
совокупности фирм по признакам Среднесписочная численность менеджеров и Объём
продаж, включая:
·
изучение структуры совокупности по признаку Среднесписочная
численность менеджеров;
·
выявление наличия корреляционной связи между
признаками Среднесписочная численность менеджеров и Объём продаж
фирм, установление направления связи и оценка её тесноты;
·
применение выборочного метода для определения
статистических характеристик генеральной совокупности фирм.
Задание 1
По исходным данным (табл. 1)
необходимо выполнить следующее:
1.
Построить статистический ряд распределения фирм по среднесписочной
численности менеджеров, образовав шесть групп с равными
интервалами.
2.
Графическим методом и путем расчетов определить
значения моды и медианы полученного ряда распределения.
3.
Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации.
4.
Вычислить среднюю
арифметическую по исходным данным (табл. 1), сравнить её с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения. Объяснить
причину их расхождения.
Сделать
выводы по результатам выполнения Задания 1.
Выполнение
Задания 1
Целью выполнения
данного Задания
является изучение состава и структуры выборочной совокупности фирм путем
построения и анализа статистического ряда распределения фирм по признаку Среднесписочная
численность менеджеров.
1. Построение интервального ряда распределения фирм по
среднесписочной численности менеджеров
Для построения
интервального ряда распределения определяем величину интервала h по формуле:
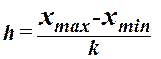 ,
,
где 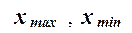 –наибольшее
и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
–наибольшее
и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
При заданных k = 6,
xmax = 50 чел. и xmin
= 20 чел.
h = 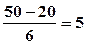 чел.
чел.
При
h = 5 чел. границы
интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица 2
|
Номер группы
|
Нижняя граница, чел.
|
Верхняя граница, чел.
|
|
1
|
20
|
25
|
|
2
|
25
|
30
|
|
3
|
30
|
35
|
|
4
|
35
|
40
|
|
5
|
40
|
45
|
|
6
|
45
|
50
|
Определяем
число фирм, входящих в каждую группу, используя принцип полуоткрытого интервала [ ), согласно которому фирмы со значениями признаков,
которые служат одновременно верхними и нижними границами смежных интервалов
(25, 30, 35, 40 и 45 чел.), будем относить ко второму из смежных интервалов.
Для определения числа фирм в
каждой группе строим разработочную
таблицу 3 (данные графы 4 потребуются при выполнении Задания 2).
Таблица 3
Разработочная таблица для построения интервального
ряда распределения и аналитической группировки
|
Группы фирм по
среднесписочной численности
менеджеров, чел.
|
Номер
фирмы
|
Среднесписочная
численность менеджеров,
чел.
|
Объем продаж,
млн руб.
|
|
1
|
2
|
3
|
4
|
|
20 – 25
|
3
|
20
|
2,50
|
|
|
12
|
22
|
2,60
|
|
|
4
|
24
|
2,60
|
|
Всего
|
3
|
66
|
7,70
|
|
25 – 30
|
13
|
25
|
2,80
|
|
|
2
|
26
|
2,80
|
|
|
10
|
27
|
2,90
|
|
|
7
|
28
|
2,9 0
|
|
Всего
|
4
|
106
|
11,40
|
|
30 – 35
|
5
|
30
|
3,00
|
|
|
17
|
31
|
3,00
|
|
|
20
|
31
|
3,00
|
|
|
15
|
32
|
3,10
|
|
|
6
|
33
|
3,10
|
|
|
18
|
33
|
3,30
|
|
Всего
|
6
|
190
|
18,50
|
|
35-40
|
1
|
35
|
3,30
|
|
|
8
|
35
|
3,40
|
|
|
14
|
35
|
3,35
|
|
|
11
|
36
|
3,30
|
|
|
21
|
36
|
3,35
|
|
|
22
|
36
|
3,45
|
|
|
23
|
37
|
3,47
|
|
|
24
|
37
|
3,50
|
|
|
25
|
38
|
3,60
|
|
|
26
|
39
|
3,70
|
|
Всего
|
10
|
364
|
34,42
|
|
40-45
|
19
|
41
|
3,50
|
|
|
9
|
42
|
3,60
|
|
|
27
|
43
|
3,60
|
|
|
28
|
44
|
4,00
|
|
Всего
|
4
|
170
|
14,70
|
|
45-50
|
29
|
46
|
3,90
|
|
|
30
|
48
|
3,80
|
|
|
16
|
50
|
4,00
|
|
Всего
|
3
|
144
|
11,70
|
|
Итого
|
30
|
1040
|
98,42
|
На основе
групповых итоговых строк «Всего» табл. 3 формируем итоговую таблицу 4,
представляющую интервальный ряд распределения фирм по среднесписочной численности менеджеров.
Таблица 4
Распределение фирм по среднесписочной
численности менеджеров
|
Номер
группы
|
Группы фирм по
среднесписочной численности менеджеров, чел.,
x
|
Число фирм,
fj
|
|
1
|
20-25
|
3
|
|
2
|
25-30
|
4
|
|
3
|
30-35
|
6
|
|
4
|
35-40
|
10
|
|
5
|
40-45
|
4
|
|
6
|
45-50
|
3
|
|
|
ИТОГО
|
30
|
Приведем еще
три характеристики полученного ряда распределения - частоты групп в относительном выражении, накопленные (кумулятивные)
частоты Sj, получаемые путем последовательного суммирования частот всех
предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле 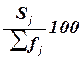 .
.
Таблица 5
Структура фирм по
среднесписочной численности менеджеров
|
Номер
группы
|
Группы фирм по
среднесписочной численности менеджеров, чел.,
x
|
Число фирм,
f
|
Накопленная частота
Sj
|
Накопленная
частость, %
|
|
в абсолютном
выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
20-25
|
3
|
10
|
3
|
10
|
|
2
|
25-30
|
4
|
13
|
7
|
23
|
|
3
|
30-35
|
6
|
20
|
13
|
43
|
|
4
|
35-40
|
10
|
34
|
23
|
77
|
|
5
|
40-45
|
4
|
13
|
27
|
90
|
|
6
|
45-50
|
3
|
10
|
30
|
100
|
|
|
ИТОГО
|
30
|
100
|
|
|
Вывод. Анализ интервального ряда
распределения изучаемой совокупности фирм показывает, что распределение фирм по
среднесписочной численности менеджеров не является равномерным: преобладают
фирмы со среднесписочной численностью менеджеров от 35 чел. до 40 чел. (это 10
фирм, доля которых составляет 34%); самые малочисленные группы фирм имеют 25-30
чел. и 45-50 чел., каждая из которых включает 3 фирмы, что составляет по 10% от
общего числа фирм.
2.
Нахождение моды и медианы полученного интервального ряда распределения
графическим методом и путем расчетов
Для определения моды графическим методом строим по данным табл. 4
(графы 2 и 3) гистограмму распределения фирм по изучаемому признаку.
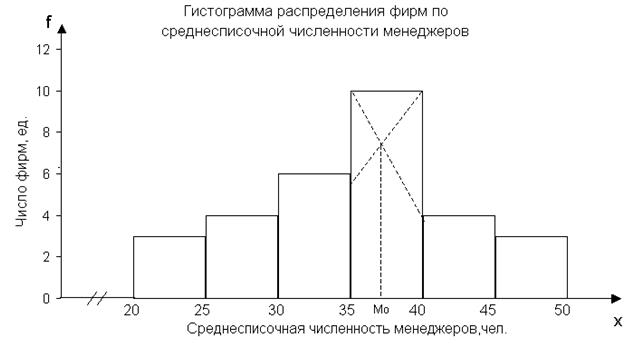
Рис. 1. Определение
моды графическим методом
Расчет конкретного значения моды для
интервального ряда распределения производится по формуле:
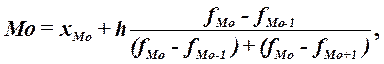
где
хМo – нижняя граница модального
интервала,
h – величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным.
Согласно табл. 4
модальным интервалом построенного ряда является интервал 35 - 40 чел., т.к. он
имеет наибольшую частоту (f4=10). Расчет моды:
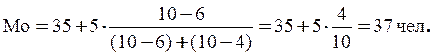
Вывод. Для рассматриваемой совокупности
фирм наиболее распространенная среднесписочная численность менеджеров
характеризуется средней величиной
37 человек.
Для определения медианы графическим методом строим по данным табл.
5 (графы 2 и 5) кумуляту распределения фирм по изучаемому признаку.
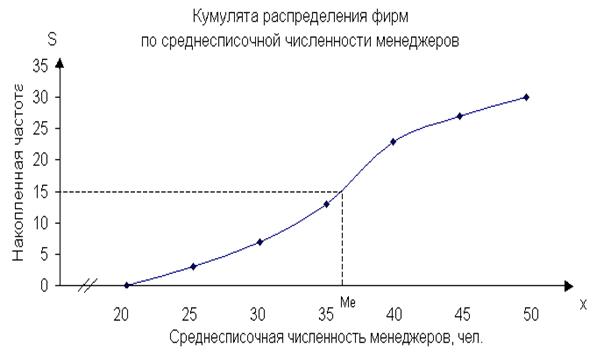
Рис. 2. Определение медианы
графическим методом
Расчет конкретного значения медианы для интервального ряда
распределения производится по формуле
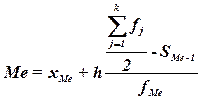 ,
,
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
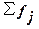 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Определяем медианный
интервал, используя графу 5 табл. 5. Медианным интервалом является интервал
35-40 чел., т.к. именно в этом интервале накопленная частота Sj=23 впервые превышает полусумму всех частот (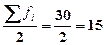 ).
).
Расчет медианы:
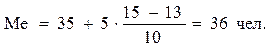
Вывод. В рассматриваемой совокупности фирм
половина фирм имеют среднесписочную численность менеджеров не более 36 человек,
а другая половина – не менее 36 человек.
3. Расчет
характеристик ряда распределения
Для расчета характеристик ряда распределения 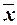 , σ, σ2, Vσ на основе табл. 5 строим
вспомогательную таблицу 6 (
, σ, σ2, Vσ на основе табл. 5 строим
вспомогательную таблицу 6 (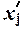 – середина интервала).
– середина интервала).
Таблица 6
Расчетная таблица для
нахождения характеристик ряда распределения
|
Группы
фирм по среднесписочной численности менеджеров, чел.
|
Середина интервала,
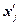
|
Число фирм,
fj
|
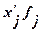
|
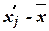
|
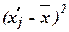
|
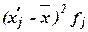
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
20-25
|
22,5
|
3
|
67,5
|
-12,833
|
164,6859
|
494,0577
|
|
25-30
|
27,5
|
4
|
110,0
|
-7,833
|
61,3559
|
245,4236
|
|
30-35
|
32,5
|
6
|
195,0
|
-2,833
|
8,0259
|
48,1553
|
|
35-40
|
37,5
|
10
|
375,0
|
2,167
|
4,6959
|
46,9589
|
|
40-45
|
42,5
|
4
|
170,0
|
7,167
|
51,3659
|
205,4636
|
|
45-50
|
47,5
|
3
|
142,5
|
12,167
|
148,0359
|
444,1077
|
|
ИТОГО
|
|
30
|
1060,0
|
|
|
1484,16668
|
Рассчитаем среднюю арифметическую
взвешенную:
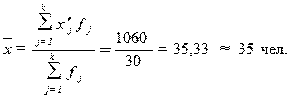
Рассчитаем среднее квадратическое
отклонение:
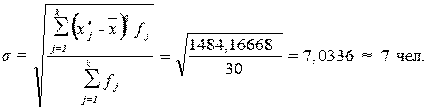
Рассчитаем дисперсию:
σ2 = 7,03362 = 49,47222
Рассчитаем коэффициент вариации:
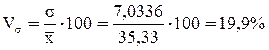
Вывод. Анализ полученных значений
показателей 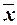 и σ говорит о том, что
средняя величина среднесписочной численности менеджеров составляет 35 чел.,
отклонение от этой величины в ту или иную сторону составляет в среднем 7 чел.
(или 19,9%), наиболее характерная среднесписочная численность менеджеров
находится в пределах от 28 до 42 чел.
(диапазон
и σ говорит о том, что
средняя величина среднесписочной численности менеджеров составляет 35 чел.,
отклонение от этой величины в ту или иную сторону составляет в среднем 7 чел.
(или 19,9%), наиболее характерная среднесписочная численность менеджеров
находится в пределах от 28 до 42 чел.
(диапазон 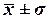 ).
).
Значение Vσ = 19,9% не превышает 33%,
следовательно, вариация среднесписочной численности менеджеров в исследуемой
совокупности фирм незначительна и совокупность по данному признаку однородна.
Расхождение между значениями 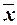 , Мо и Ме незначительно (
, Мо и Ме незначительно (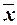 =35 чел., Мо=37
чел., Ме=36 чел.), что подтверждает
вывод об однородности совокупности фирм. Таким образом, найденное среднее
значение среднесписочной численности менеджеров (35 чел.) является типичной,
надежной характеристикой исследуемой совокупности фирм.
=35 чел., Мо=37
чел., Ме=36 чел.), что подтверждает
вывод об однородности совокупности фирм. Таким образом, найденное среднее
значение среднесписочной численности менеджеров (35 чел.) является типичной,
надежной характеристикой исследуемой совокупности фирм.
4. Вычисление средней арифметической по
исходным данным о среднесписочной
численности менеджеров фирм
Для расчета применяется формула средней арифметической
простой:
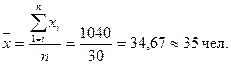 ,
,
Причина расхождения
средних величин, рассчитанных по исходным данным (34,67 чел.) и по
интервальному ряду распределения (35,33 чел.), заключается в том, что в первом
случае средняя определяется по фактическим значениям исследуемого
признака для всех 30-ти фирм, а во втором случае в качестве значений признака
берутся середины интервалов 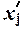 и, следовательно, значение средней будет менее
точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения
совпадают (35 чел.), что говорит о достаточно равномерном распределении
численности менеджеров внутри каждой группы интервального ряда.
и, следовательно, значение средней будет менее
точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения
совпадают (35 чел.), что говорит о достаточно равномерном распределении
численности менеджеров внутри каждой группы интервального ряда.
Задание 2
По исходным
данным (табл. 1) с использованием
результатов выполнения Задания 1 необходимо выполнить следующее:
1.
Установить наличие и характер корреляционной связи
между признаками Среднесписочная численность менеджеров и Объём продаж, образовав шесть групп с равными интервалами по
каждому из признаков, используя методы:
а) аналитической
группировки;
б)
корреляционной таблицы.
2. Измерить
тесноту корреляционной связи, используя коэффициент
детерминации и эмпирическое корреляционное отношение.
Сделать
выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью
выполнения данного задания
является выявление наличия корреляционной связи между факторным и
результативным признаками, а также установление направления связи и оценка ее
тесноты.
По условию
Задания 2 факторным является признак Среднесписочная численность менеджеров,
результативным – признак Объем продаж.
1. Установление наличия и характера
корреляционной связи между признаками Среднесписочная численность менеджеров
и
Объём продаж методами аналитической группировки и корреляционных
таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится
по факторному признаку Х и для
каждой j-ой группы ряда
определяется среднегрупповое значение 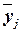 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 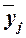 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку,
характеризующую зависимость между факторным признаком Х- Среднесписочная численность менеджеров и результативным
признаком Y - Объём продаж. Макет
аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7
Зависимость объема продаж от
среднесписочной численности менеджеров
|
Номер группы
|
Группы фирм по
среднесписочной численности менеджеров, чел.,
x
|
Число фирм,
fj
|
Объем продаж, млн
руб.
|
|
всего
|
в среднем на одну
фирму,
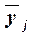
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
|
ИТОГО
|
|
|
|
Групповые средние значения 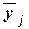 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8:
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8:
Таблица 8
Зависимость объема продаж от
среднесписочной численности менеджеров
|
Номер группы
|
Группы фирм по
среднесписочной численности менеджеров, чел.,
x
|
Число фирм,
fj
|
Объем продаж, млн
руб.
|
|
всего
|
в среднем на одну
фирму,

|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
20-25
|
3
|
7,70
|
2,5667
|
|
2
|
25-30
|
4
|
11,40
|
2,8500
|
|
3
|
30-35
|
6
|
18,50
|
3,0833
|
|
4
|
35-40
|
10
|
34,42
|
3,4420
|
|
5
|
40-45
|
4
|
14,70
|
3,6750
|
|
6
|
45-50
|
3
|
11,70
|
3,9000
|
|
|
ИТОГО
|
30
|
98,42
|
|
Вывод. Анализ данных табл. 8 показывает, что с увеличением
среднесписочной численности менеджеров от группы к группе систематически
возрастает и средний объем продаж по каждой группе фирм, что свидетельствует о
наличии прямой корреляционной связи между исследуемыми признаками.
1б.
Применение метода корреляционных таблиц
Корреляционная
таблица строится как комбинация двух рядов распределения по факторному признаку
Х и результативному признаку Y. На
пересечении j-ой строки
и k-ой графы
таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый
интервал по признаку Y.
Концентрация частот около диагонали построенной таблицы свидетельствует о
наличии корреляционной связи между признаками - прямой или обратной. Связь
прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла
к правому нижнему, обратная - по диагонали от правого верхнего угла к левому
нижнему.
Для
построения корреляционной таблицы необходимо знать величины и границы
интервалов по двум признакам X и Y. Для
факторного признака Х – Среднесписочная
численность менеджеров эти
величины известны из табл. 4
Определяем величину интервала для результативного признака Y – Объем продаж при k = 6, уmax = 4,0 млн руб., уmin = 2,5 млн руб.:
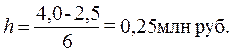
Границы интервалов ряда распределения
результативного признака Y имеют вид:
Таблица 9
|
Номер группы
|
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
|
1
|
2,50
|
2,75
|
|
2
|
2,75
|
3,00
|
|
3
|
3,00
|
3,25
|
|
4
|
3,25
|
3,50
|
|
5
|
3,50
|
3,75
|
|
6
|
3,75
|
4,00
|
Подсчитывая для каждой группы число входящих в нее фирм с
использованием принципа полуоткрытого интервала [ ), получаем интервальный
ряд распределения результативного признака (табл. 10).
Таблица 10
Интервальный ряд
распределения фирм по объёму продаж
|
Группы фирм по объёму продаж, млн руб.,
у
|
Число фирм,
fj
|
|
2,50-2,75
|
3
|
|
2,75-3,00
|
4
|
|
3,00-3,25
|
5
|
|
3,25-3,50
|
8
|
|
3,50-3,75
|
6
|
|
3,75-4,00
|
4
|
|
ИТОГО
|
30
|
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу (табл. 11).
Таблица
11
Корреляционная таблица зависимости объема продаж
от среднесписочной
численности менеджеров
|
Группы
фирм по среднесписочной численности менеджеров, чел.
|
Группы
фирм по объёму продаж, млн руб.
|
ИТОГО
|
|
2,50-2,75
|
2,75-3,00
|
3,00-3,25
|
3,25-3,50
|
3,50-3,75
|
3,75-4,00
|
|
20-25
|
3
|
|
|
|
|
|
3
|
|
25-30
|
|
4
|
|
|
|
|
4
|
|
30-35
|
|
|
5
|
1
|
|
|
6
|
|
35-40
|
|
|
|
7
|
2
|
1
|
10
|
|
40-45
|
|
|
|
|
4
|
|
4
|
|
45-50
|
|
|
|
|
|
3
|
3
|
|
ИТОГО
|
3
|
4
|
5
|
8
|
6
|
4
|
30
|
Вывод. Анализ
данных табл. 11 показывает, что распределение частот групп произошло вдоль
диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это
свидетельствует о наличии прямой корреляционной связи между среднесписочной
численностью менеджеров и объемом продаж фирмами.
2. Измерение тесноты корреляционной связи с использованием коэффициента
детерминации 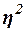 и эмпирического корреляционного отношения
и эмпирического корреляционного отношения 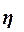
Коэффициент детерминации 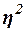 характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии
характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии 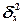 признака Y в его
общей дисперсии
признака Y в его
общей дисперсии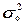 :
:
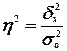
где 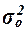 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
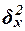 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая
дисперсия 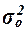 характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
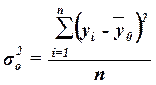 ,
(10)
,
(10)
где yi – индивидуальные значения
результативного признака;
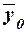 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия 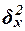 измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
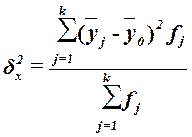 ,
(13)
,
(13)
где 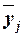 –групповые
средние,
–групповые
средние,
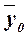 –
общая средняя,
–
общая средняя,
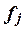 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета показателей 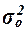 и
и 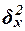 необходимо знать
величину общей средней
необходимо знать
величину общей средней 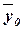 , которая вычисляется
как средняя
арифметическая простая по всем единицам совокупности:
, которая вычисляется
как средняя
арифметическая простая по всем единицам совокупности:
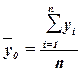
Значения числителя и знаменателя формулы имеются
в табл. 8 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую
среднюю 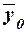 :
:
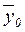 =
=
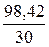 =3,281 млн руб.
=3,281 млн руб.
Для
расчета общей дисперсии 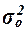 применяется вспомогательная таблица
12.
применяется вспомогательная таблица
12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
|
Номер
фирмы
|
Объём продаж, млн.
руб.
|
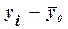
|
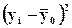
|
|
1
|
2
|
3
|
4
|
|
1
|
3,30
|
0,019
|
0,0004
|
|
2
|
2,80
|
0,481
|
0,2310
|
|
3
|
2,50
|
0,781
|
0,6094
|
|
4
|
2,60
|
0,681
|
0,4633
|
|
5
|
3,00
|
0,281
|
0,0788
|
|
6
|
3,10
|
0,181
|
0,0326
|
|
7
|
2,90
|
0,381
|
0,1449
|
|
8
|
3,40
|
0,119
|
0,0142
|
|
9
|
3,60
|
0,319
|
0,1020
|
|
10
|
2,90
|
0,381
|
0,1449
|
|
11
|
3,30
|
0,019
|
0,0004
|
|
12
|
2,60
|
0,681
|
0,4633
|
|
13
|
2,80
|
0,481
|
0,2310
|
|
14
|
3,35
|
0,069
|
0,0048
|
|
15
|
3,10
|
0,181
|
0,0326
|
|
16
|
4,00
|
0,719
|
0,5174
|
|
17
|
3,00
|
0,281
|
0,0788
|
|
18
|
3,30
|
0,019
|
0,0004
|
|
19
|
3,50
|
0,219
|
0,0481
|
|
20
|
3,00
|
0,281
|
0,0788
|
|
21
|
3,35
|
0,069
|
0,0048
|
|
22
|
3,45
|
0,169
|
0,0287
|
|
23
|
3,47
|
0,189
|
0,0358
|
|
24
|
3,50
|
0,219
|
0,0481
|
|
25
|
3,60
|
0,319
|
0,1020
|
|
26
|
3,70
|
0,419
|
0,1758
|
|
27
|
3,60
|
0,319
|
0,1020
|
|
28
|
4,00
|
0,719
|
0,5174
|
|
29
|
3,90
|
0,619
|
0,3836
|
|
30
|
3,80
|
0,519
|
0,2697
|
|
Итого
|
98,42
|
|
4,9452
|
Рассчитаем общую
дисперсию:
 =
=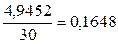
Для расчета межгрупповой дисперсии 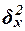 строится вспомогательная таблица 13 При этом используются групповые средние значения
строится вспомогательная таблица 13 При этом используются групповые средние значения 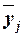 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой дисперсии
|
Группы фирм по
среднесписочной численности менеджеров, чел.,
x
|
Число
фирм,
fj
|
Среднее значение в
группе, млн руб.
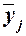
|
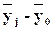
|

|
|
1
|
2
|
3
|
4
|
5
|
|
20-25
|
3
|
2,567
|
-0,714
|
1,5294
|
|
25-30
|
4
|
2,850
|
-0,431
|
0,7420
|
|
30-35
|
6
|
3,083
|
-0,197
|
0,2338
|
|
35-40
|
10
|
3,442
|
0,161
|
0,2602
|
|
40-45
|
4
|
3,675
|
0,394
|
0,6219
|
|
45-50
|
3
|
3,900
|
0,619
|
1,1506
|
|
ИТОГО
|
30
|
|
|
4,5379
|
Рассчитаем межгрупповую дисперсию:
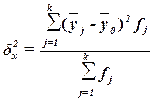
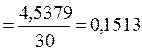
Определяем
коэффициент детерминации:
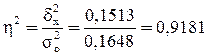 или
91,8%
или
91,8%
Вывод. 91,8% вариации объёма продаж
товаров фирмами обусловлено вариацией среднесписочной численности менеджеров по
продажам, а 8,2% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение 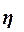 оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
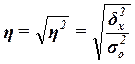
Рассчитаем
показатель 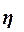 :
:

Вывод: согласно
шкале Чэддока связь между среднесписочной численностью менеджеров и объёмом
продаж фирмами является весьма тесной.
Задание 3
По
результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1) ошибку
выборки для средней величины
среднесписочной численности менеджеров, а также границы, в которых будет
находиться генеральная средняя.
2)
ошибку выборки
доли фирм со среднесписочной численностью менеджеров 40 человек и более, а
также границы, в которых будет находиться генеральная доля фирм.
Выполнение Задания 3
Целью выполнения
данного Задания
является определение для генеральной совокупности фирм региона границ, в
которых будут находиться средняя величина среднесписочной
численности менеджеров,
и доля фирм со среднесписочной численностью
менеджеров не менее 40
человек.
1.
Определение ошибки выборки для величины
среднесписочной численности менеджеров, а также границ, в которых будет
находиться генеральная средняя
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные харак- теристики, как
правило, не совпадают, а отклоняются на некоторую величину ε.
Принято вычислять два вида
ошибок выборки - среднюю  и предельную
и предельную  .
.
Для расчета средней ошибки выборки  применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической выборки с бесповторным способом отбора средняя ошибка  для выборочной средней
для выборочной средней 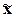 определяется по
формуле
определяется по
формуле
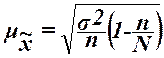 ,
,
где 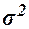 – общая дисперсия изучаемого признака,
– общая дисперсия изучаемого признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки  определяет границы, в пределах
которых будет находиться генеральная средняя:
определяет границы, в пределах
которых будет находиться генеральная средняя:
 ,
,
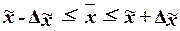 ,
,
где 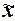 – выборочная средняя,
– выборочная средняя,
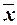 – генеральная средняя.
– генеральная средняя.
Предельная
ошибка выборки  кратна средней ошибке
кратна средней ошибке  с коэффициентом кратности t (называемым также коэффициентом доверия):
с коэффициентом кратности t (называемым также коэффициентом доверия):
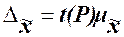
Коэффициент
кратности t зависит от
значения доверительной вероятности
Р, гарантирующей вхождение генеральной средней в интервал 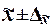 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им
значения t задаются следующим образом (табл. 14):
Таблица 14
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию Задания 2 выборочная совокупность насчитывает 30
фирм, выборка 10% механическая, следовательно, генеральная совокупность включает
300 фирм. Выборочная средняя 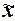 , дисперсия
, дисперсия 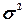 определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
Таблица 15
|
Р
|
t
|
n
|
N
|

|
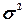
|
|
0,954
|
2
|
30
|
300
|
35,33
|
49,4722
|
Рассчитаем среднюю ошибку выборки:
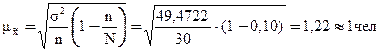
Рассчитаем
предельную ошибку выборки:
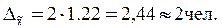
Определим
доверительный интервал для генеральной средней:

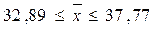
или
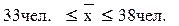
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,954 можно утверждать, что для
генеральной совокупности фирм средняя величина среднесписочной численности
менеджеров находится в пределах от 33 до 38 человек.
2. Определение
ошибки выборки для доли фирм со среднесписочной численностью менеджеров 40 человек и более, а также границ, в которых
будет находиться генеральная доля
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
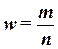 ,
,
где m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для собственно-случайной
и механической выборки с бесповторным способом отбора предельная
ошибка выборки 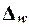 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
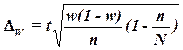 ,
,
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная ошибка выборки 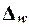 определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
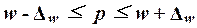
По
условию Задания 3 исследуемым свойством фирм является равенство или превышение
среднесписочной численности менеджеров величины 40 человек.
Число
фирм с данным свойством определяется из табл. 3 (графа 3):
m=7
Рассчитаем
выборочную долю:

Рассчитаем
предельную ошибку выборки для доли:
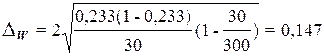
Определим
доверительный интервал генеральной доли:
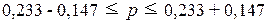
0,086 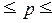 0,380
0,380
или
8,6% 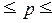 38%
38%
Вывод. С вероятностью
0,954 можно утверждать, что в генеральной совокупности фирм региона доля фирм
со среднесписочной численностью менеджеров
40 человек и более будет находиться в пределах от 8,6% до 38%.
Литература
1.
Громыко Г.Л. Теория статистики: Учебник. -
М.: ИНФРА-М, 2006.
2.
Громыко Г.Л. Теория статистики: Практикум. -
М.: ИНФРА-М, 2003.
3. Гусаров В.М. Статистика:
Учеб. пособие для вузов. - М.: ЮНИТИ - ДАНА, 2001.
4.
Гусаров В.М. Статистика: Учеб пособие/ В.М. Гусаров, Е.И. Кузнецова. –
2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
5. Общая теория статистики:
Статистическая методология в изучении коммерческой деятельности: Учебник / Под.
ред. Башиной О.Э., Спирина А.А. – М.: Финансы и статисика, 2005.
6. Практикум по статистике:
Учеб. пособие для вузов/ Под ред. В.М. Симчеры. - М.: Финстатинформ, 1999.
7. Практикум по теории
статистики: Учебное пособие/Под. ред. Шмойловой Р.А. – М.: Финансы и
статистика, 2004.
8. Сироткина Т.С., Каманина
А.М. Основы теории статистики: Учеб. пособие для вузов/ Под ред. проф. В.М.
Симчеры. - М.: Финстатинформ, 1995, 1996.
9. Статистика: Учеб.
пособие/А.В. Багат, М.М. Конкина, В.М. Симчера и др.; Под ред. В.М. Симчеры.-
М.: Финансы и статистика, 2005.
10.
Теория статистики: Учебник/Под. ред. Шмойловой Р.А. – М.: Финансы и
статистика, 2001; 2003; 2006.
Содержание
Введение
………………………………………………………………..
Раздел I Методические рекомендации к выполнению
статистических
расчётов…………………………….............................
Задание
1……………………………………………………………………………
Задание
2……………………………………………………………………………
Задание
3……………………………………………………………………………
Раздел II Образец
выполнения оформления Заданий 1-3
курсовых
и контрольных работ………………………………………..
Задание
1……………………………………………………………………………
Задание
2……………………………………………………………………………
Задание
3……………………………………………………………………………
Литература……………………………………………………………...
[1] Если в дискретном ряду все варианты встречаются
одинаково часто, то в этом случае мода отсутствует. Могут быть распределения,
где не один, а два (или более) варианта имеют наибольшие частоты. Тогда ряд
имеет две (или более) моды, распределение является бимодальным (или
многомодальным),что указывает на качественную неоднородность совокупности по
изучаемому признаку.