СОДЕРЖАНИЕ

Задача 6. 2

Задача 14. 3

Задача 21. 5

Задача 28. 9

Задача 36. 10

Задача 45. 12

СПИСОК ЛИТЕРАТУРЫ.. 15

Задача 6.

Имеются данные о затратах сырья и объемах производства:

Технология	Период
Базисный	Отчетный
Затраты на производство единицы изделия, кг	Объем производства, шт.	Затраты на производство единицы изделия, кг	Общие затраты сырья, тыс. кг
Старая	6,3	456	5,7	3,2
Новая	4,8	432	4,8	2,6

Определить средние затраты сырья за базисный и отчетный период.

Решение

Вид и форма средней выбирается исходя из экономического содержания исчисленного показателя.

В условии задачи имеются данные об объеме производства и затратах на производство единицы изделия, то исходя из экономического содержания показателя для определения средних затрат сырья за базисный период, применяется средняя арифметическая взвешенная:

, (1)

где х – затраты сырья,

f – объем производства.

Средние затраты сырья за базисный период составят:

Так как по условию задачи отсутствуют данные о частоте появления признака, но имеется информация об общем значении признака (общих затрат сырья), то для расчета средних затрат сырья за базисный период применяем формулу средней гармонической взвешенной:

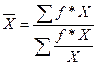(2)

Средние затраты сырья за отчетный период составят:

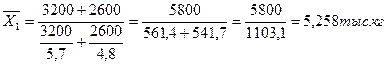
Задача 14.

Для изучения зависимости между сменой работы и производительностью труда рассчитайте эмпирическое корреляционное отношение и коэффициент детерминации. Сделайте вывод.

Смена	Выработка, шт. на чел.
1	5 8 8 4 2 6
2	4 6 8 7 4 9 1

Решение

Коэффициент детерминации определяется по формуле

, (3)

где ─ межгрупповая дисперсия;

─ общая дисперсия.

Коэффициент детерминации характеризует долю вариации результативного признака, обусловленную изменчивостью изучаемого фактора.

Оценить тесноту связи можно по величине эмпирического корреляционного отношения, используя формулу

(4)

Эмпирическое корреляционное отношение изменяется , – при отсутствии связи, – при функциональной зависимости.

Межгрупповая дисперсия отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки:

, (5)

где ─ средние значения результативного признака в соответствующих группах;

─ общая средняя для всей совокупности;

f_i ─ число наблюдений в соответствующей группе.

Величина общей дисперсии характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц совокупности.

(6)

где ─ общая средняя арифметическая для всей изучаемой совокупности;

─ значение признака.

Для расчета показателей вариации составим вспомогательную таблицу 1.

Таблица 1

Расчет показателей вариации

Смена	Число наблюдений (f)	Выработка, шт. на чел.
1	1	2	-3,5385	12,5210	12,5210
1	4	-1,5385	2,3670	2,3670
1	5	0,5385	0,2900	0,2900
1	6	0,4615	0,2130	0,2130
2	8	2,4615	6,0590	12,118
Итого:	6	33	─	─	27,509
2	1	1	-4,5385	20,5980	20,5980
2	4	-1,5385	2,3670	4,7340
1	6	0,4615	0,2130	0,2130
1	7	1,4615	2,1360	2,1360
1	8	2,4615	6,0590	6,0590
1	9	3,4615	11,9820	11,9820
Итого:	7	39	─	─	45,7220
ВСЕГО:	13	72	─	─	73,2310

Средняя для первой смены составит:

Средняя для второй смены составит:

Общая средняя арифметическая для всей изучаемой совокупности:

шт. на чел.

Найдем общую дисперсию по формуле (6):

Найдем межгрупповую дисперсию по формуле (5):

Определим коэффициент детерминации по формуле (3):

или 0,45%

Коэффициент детерминации показывает, что производительность труда на 0,45% зависит от смены и на 99,55% от других факторов.

Эмпирическое корреляционное отношение составит:

Это говорит о том, что связь между сменой работы и производительностью труда отсутствует, смена работы не влияет на производительность труда.

Задача 21.

В таблице представлены результаты 10-ти процентного выборочного обследования затрат времени на просмотр телепередач:

Затраты времени на просмотр телепередач, мин в сутки	Число опрошенных, тыс. чел.
До 60	4
60 – 90	22
90 – 120	35
120 – 150	16
150 – 180	12
Итого	89

Определите: 1) коэффициент вариации; 2) с вероятностью 0,997 пределы, в которых изменяются средние затраты времени на просмотр телепередач всех жителей региона; 3) с вероятностью 0,954 пределы, в которых изменяется доля жителей, затрачивающих на просмотр телепередач менее 1 часа.

Решение

Коэффициент вариации определяется по формуле:

, (7)

Коэффициент вариации показывает степень однородности совокупности. Если V < 33% − совокупность однородна.

Среднее выборочное значение определяется по формуле средней арифметической взвешенной:

(8)

Среднее квадратическое отклонение определяется по формуле:

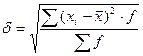(9)

Для удобства расчетов составим вспомогательную таблицу 2.

Таблица 2

Затраты времени на просмотр телепере-дач, мин в сутки	Число опрошен-ных, тыс. чел. (f)	Сере-дина интерва-ла (х)	Накоп-ленная частота (S)	xf		()²	(х-)²*f
(30) До 60	4	45	4	190	-63,48	4029,71	16118,8
60-90	22	75	26	1650	-33,48	1120,91	24660,0
90-120	35	105	61	3675	-3,48	12,11	423,8
120-150	16	135	77	2160	26,52	703,31	11252,9
150-180	12	165	89	1980	56,52	3194,51	38334,1
ИТОГО:	89	─	─	9655	─	─	90789,6

Средние затраты времени на просмотр телепередач составят:

мин в сутки

Среднее квадратическое отклонение составит:

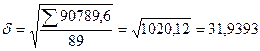мин в сутки

Коэффициент вариации составит:

Коэффициент вариации меньше 30 %, значит, совокупность однородная и средняя – надежная.

Границы генеральной средней определяются как

, (10)

где − генеральная средняя,

− выборочная средняя,

Δ− предельная ошибка выборочной средней:

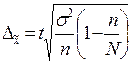, (11)

где − коэффициент доверия, зависящий от того, с какой вероятностью

определяется предельная ошибка: при вероятности 0,997 он

равен 3, при 0,954 – 2.

n – объем выборочной совокупности,

N – объем генеральной совокупности, N = 890 (так как отбор составляет 10%).

− дисперсия признака выборочной совокупности.

Предельная ошибка выборочной средней составит:

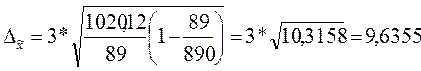
Найдем пределы, в которых изменяются средние затраты времени на просмотр телепередач всех жителей региона с вероятностью 0,997:

Средние затраты времени на просмотр телепередач находятся в пределах 98,8476≤≤118,1186 с вероятностью 0,997.

Определим пределы, в которых изменяется доля жителей, затрачивающих на просмотр телепередач менее 1 часа с вероятностью 0,954.

Границы генеральной доли находятся как

, (12)

где р – генеральная доля,

− выборочная доля:

, (13)

где − число единиц, обладающих данным признаком,

n − объем выборочной совокупности.

− предельная ошибка доли:

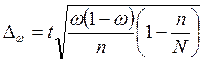. (14)

Определим выборочную долю:

Тогда предельная ошибка доли составит:

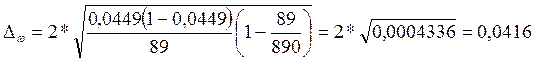
Определим границы генеральной доли:

Доля жителей, затрачивающих на просмотр телепередач менее 1 часа, изменяется в пределах 0,0033≤р≤0,0865 с вероятностью 0,954.

Задача 28.

По заводу имеются следующие данные о выпуске продукции:

Вид продукции	Выпуск продукции в тыс. руб.	Увеличение (+) или уменьшение (-) выпуска продукции во 2 квартале по сравнению с 1 кварталом, %
Квартал
1	2
Рельсы трамвайные Чугун литейный Железо листовое	22 300 15 800 10 500	24 500 16 100 9 800	+3,0 -2,0 +1,5

Определите общие индексы физического объема, стоимости продукции и цен. Сделайте выводы.

Решение

Средний арифметический индекс физического объема продукции вычисляется по формуле:

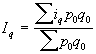(15)

По условию задачи имеются данные об увеличении или уменьшении выпуска продукции во 2 квартале по сравнению с 1 кварталом по видам продукции. Индивидуальные индексы объема выпуска продукции составляют:

i_q_{(рельсы)} = 1,03

i_q_(чугун) = 0,98

i_q_{(железо)} = 1,015

Найдем общий индекс физического объема по трем видам продукции:

, или 101,05%

Общий индекс стоимости продукции, или товарооборота представляет собой соотношение стоимости продукции текущего периода к стоимости продукции в базисном периоде и определяется по формуле:

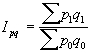(16)

Общий индекс стоимости продукции по трем видам продукции составит:

, или 103,7%

Индекс цен находим исходя из взаимосвязи соответствующих индексов – индекса стоимости, индекса физического объема и индекса цен:

(17)

Общий индекс цен по трем видам продукции составит:

, или 102,62%

По результатам рассчитанных индексов можно сделать следующие выводы: во 2-ом квартале по сравнению первым кварталом стоимость трех видов продукции увеличилась на 3,7% за счет увеличения выпуска продукции на 1,05% и увеличения цен на 2,62%.

Задача 36.

Имеются данные о выручке предприятия от поставок продукции на экспорт продукции А:

Страна импортер

Период

базисный

отчетный

Внешнеторговая цена (в долл)

(р₀)

Удельный вес поставок в натуральном выражении

(d₀)

Внешнеторговая цена (в долл)

(р₁)

Удельный вес поста-вок в нату-ральном выраже-нии (d₁)

США

Япония

Китай

100

0,7

0,1

0,2

102

0,39

0,22

0,39

Рассчитать индексы внешнеторговой цены переменного, постоянного состава, индекс структурных сдвигов. Сделайте выводы.

Решение

Индекс внешнеторговой цены переменного состава определяется по следующей формуле:

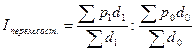(18)

Индекс внешнеторговой цены переменного состава составит:

= 1,0044, или 100,44%

Индекс внешнеторговой цены постоянного состава определяется по формуле:

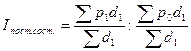(19)

Индекс внешнеторговой цены постоянного состава составит:

= 1,0165, или 101,65 %

Индекс внешнеторговой цены структурных сдвигов определяется по формуле:

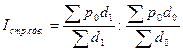(20)

Индекс внешнеторговой цены структурных сдвигов составит:

= 0,9882, или 98,82 %

Поскольку индекс цен переменного состава равен 1,0044, или 100,44%, то средняя внешнеторговая цена по трем странам импортерам увеличилась на 0,44%. Индекс цен постоянного состава равен 1,0165, или 101,65%, значит, средняя внешнеторговая цена по трем странам импортерам увеличилась на 1,65%. Индекс структурных сдвигов равен 0,9882, значит, средняя внешнеторговая цена по трем странам импортерам снизилась на 1,18% за счет изменения структуры.

Задача 45.

Динамика производства товаров для детей представлена в таблице.

Вид товара	Производство в 1999 году	Ежегодное абсолютное снижение производства
2000	2001
Пальто из натурального меха, тыс. шт.	180,8	-43,6	32,7
Пальто из искусственного меха, тыс. шт.	728,3	12,6	21,0

Определите: среднегодовое производство, среднегодовой абсолютный прирост и среднегодовой темп прироста (снижения) каждого вида продукции.

Решение

Из исходных формул аналитических показателей ряда динамики могут быть найдены отдельные составляющие (показатели). Например, используя формулу цепного абсолютного прироста, можно определить уровень изучаемого периода:

(21)

или уровень предыдущего периода

. (22)

Определим показатели производства в 2000 и 2001 гг. исходя их данных ежегодного абсолютного снижения производства и показателей производства в 1999 году.

Производство пальто из натурального меха в 2000 г. составило 137,2 тыс. шт.(180,8-43,6), пальто из искусственного меха – 740,9 тыс. шт. (728,3+12,6).

Производство пальто из натурального меха в 2001 г. составило 169,9 тыс. шт.(137,2+32,7), пальто из искусственного меха – 761,9 тыс. шт. (740,9+21,0).

Средний уровень ряда динамики определяется по формуле:

, (23)

где у_i – уровни ряда динамики,

n – число уровней ряда динамики;

Определим среднегодовое производство:

а) пальто из натурального меха

тыс. шт.

б) пальто из искусственного меха

тыс. шт.

Средний абсолютный прирост определяется по формуле:

, (24)

где у_n– конечный уровень ряда;

Среднегодовой абсолютный прирост производства составит:

а) пальто из натурального меха

тыс. шт.

Наблюдается среднегодовое снижение производства пальто из натурального меха на 5,45 тыс. штук.

б) пальто из искусственного меха

тыс. шт.

Наблюдается среднегодовой прирост производства пальто из искусственного меха на 16,8 тыс. штук.

Средний темп прироста определяется по формуле:

, (25)

где ─ средний темп роста.

Средний темп роста определяется по формуле:

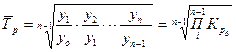, (26)

где П – знак произведения.

Средний темп роста производства составит:

а) пальто из натурального меха

В среднем за 3 года производство пальто из натурального меха снижалось на 3,07% в год.

б) пальто из искусственного меха

В среднем за 3 года производство пальто из искусственного меха увеличивалось на 2,28% в год.

СПИСОК ЛИТЕРАТУРЫ

1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.

2. Давыдова Л. А. Теория статистики в вопросах и ответах: Учебное пособие. – М.: Издательство ТК Велби, 2005. – 160 с.

3. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.

4. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.

5. Практикум по теории статистики: учебное пособие. – М.: Финансы и статистика, 1998. – 416 с.

6. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.