ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО‑ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Филиал в г. Брянске

ЛАБОРАТОРНАЯ РАБОТА

по дисциплине

ЭКОНОМЕТРИКА

ВЫПОЛНИЛ(А)

Рычкина Е.А.

СТУДЕНТ(КА)

3 курса («вечер», поток 1)

СПЕЦИАЛЬНОСТЬ

Финансы и кредит

№ ЗАЧ. КНИЖКИ

06ФФД11183

ПРЕПОДАВАТЕЛЬ

Шкаберин В.А.

Брянск — 2009

ВАРИАНТ 3

         По данным, представленным в табл. 3, изучается зависимость индекса человеческого развития[1] Y от переменных:

Ø  X1 — ВВП 1997 г., % к 1990 г.;

Ø  Х2 — расходы на конечное потребление в текущих ценах, % к ВВП;

Ø  X3 — расходы домашних хозяйств, % к ВВП;

Ø  Х4 — валовое накопление, % к ВВП;

Ø  Х5 — суточная калорийность питания населения, ккал на душу населе­ния;

Ø  Х6 — ожидаемая продолжительность жизни при рождении 1997 г., лет.

Таблица 3

Страна

Y

X1

X2

X3

X4

X5

X6

Австрия

0,904

115

75,5

56,1

25,2

3343

77

Австралия

0,922

123

78,5

61,8

21,8

3001

78,2

……………………………………………………………………………………..

Швеция

0,923

105

79

53,1

14,1

3160

78,5

Требуется

1.     Постройте матрицу парных коэффициентов корреляции. Установите, какие факторы мультиколлинеарны.

2.     Постройте уравнение множественной регрессии в линейной форме с полным набором факторов.

3.     Оцените статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

4.     Отберите информативные факторы по пунктам 1 и 3. Постройте уравне­ние регрессии со статистически значимыми факторами.

5.     Проверьте выполнение предпосылок метода наименьших квадратов, в том числе, проведите тестирование ошибок уравнения множественной рег­рессии на гетероскедастичность.

6.     Рассчитать прогнозное значение результативной переменной Y, если прогнозные значения факторов составят 75 % от своих максимальных значений. Построить доверительный интервал прогноза фактического значения Y c надежностью 80 %.

РЕШЕНИЕ

Для решения задачи используется табличный процессор EXCEL.

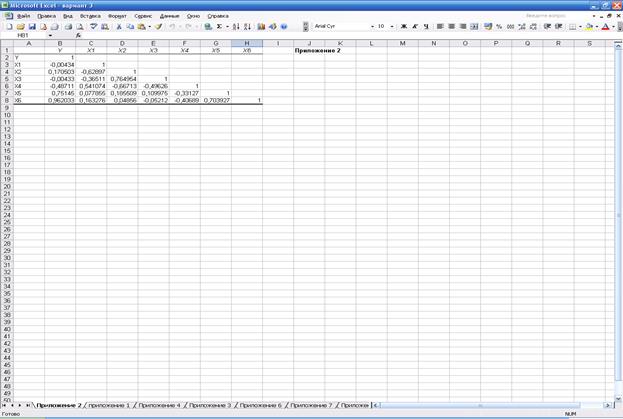
         1. С помощью надстройки «Анализ данных… Корреляция» строим матрицу парных коэффициентов корреляции между всеми исследуемыми переменными (меню «Сервис» ® «Анализ данных…» ® «Корреляция»). На рис. 1 изображена панель корреляционного анализа с заполненными полями[2]. Результаты корреляционного анализа приведены в прил. 2 и перенесены в табл. 1.

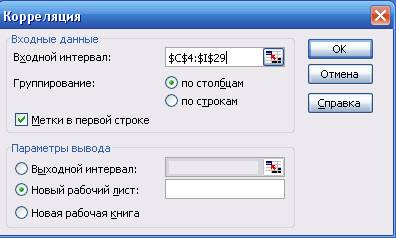
рис. 1. Панель корреляционного анализа

Таблица 1

Матрица парных коэффициентов корреляции

 

 

Y

X1

X2

X3

X4

X5

X6

Y

1

X1

-0,00434

1

X2

0,170503

-0,62897

1

X3

-0,00433

-0,36511

0,764954

1

X4

-0,48711

0,541074

-0,66713

-0,49626

1

X5

0,75145

0,077855

0,185509

0,109975

-0,33127

1

X6

0,962033

0,163276

0,04856

-0,05212

-0,40689

0,703927

1

Анализ значений парных коэффициентов корреляции между факторами Х1, Х2, …, Х6 показывает, что только коэффициент корреляции между парой факторов Y –Х6 превышает по абсолютной величине 0,8 (выделен в таблице  жирным шрифтом). Факторы Y –Х6, таким образом, признаются коллинеарными.

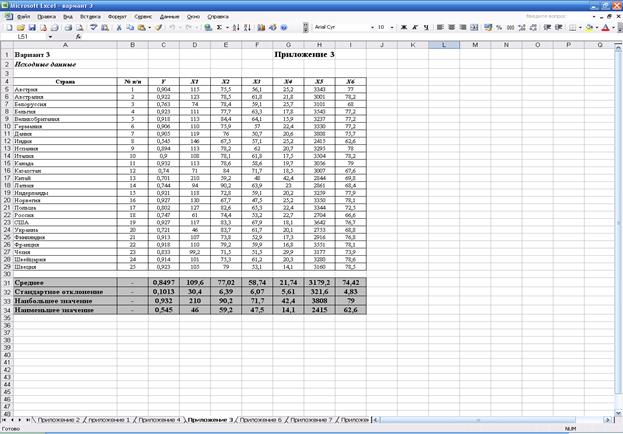
2. Для построения уравнения регрессии значения используемых переменных (Y, X1, X2, X3, X4, X5, X6) скопируем на чистый рабочий лист (прил. 3). Уравнение регрессии строим с помощью надстройки «Анализ данных… Регрессия» (меню «Сервис» ® «Анализ данных…» ® «Регрессия»). Панель регрессионного анализа с заполненными полями изображена на рис. 2.

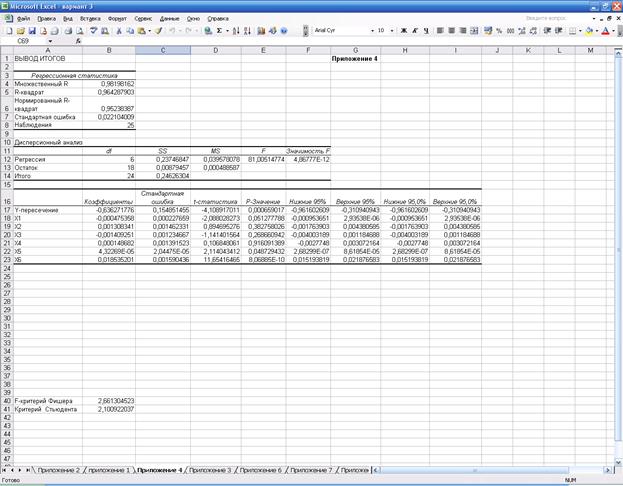
         Результаты регрессионного анализа приведены в прил. 4 и перенесены в табл. 2. Уравнение регрессии имеет вид (см. «Коэффициенты» в табл. 2):

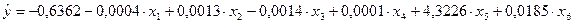
Уравнение регрессии признается статистически значимым, так как вероятность его случайного формирования в том виде, в котором оно получено, составляет 8,80×10-6 (см. «Значимость F» в табл. 2), что существенно ниже принятого уровня значимости a=0,05.

         Вероятность случайного формирования коэффициентов при факторах Х3, Х4, Х6 ниже принятого уровня значимости a=0,05 (см. «P-Значение» в табл. 2), что свидетельствует о статистической значимости коэффициентов и существенном влиянии этих факторов на изменение годовой прибыли Y.

         Вероятность случайного формирования коэффициентов при факторах Х2 и Х5 превышает принятый уровень значимости a=0,05 (см. «P-Значение» в табл. 2), и эти коэффициенты не признаются статистически значимыми.

 

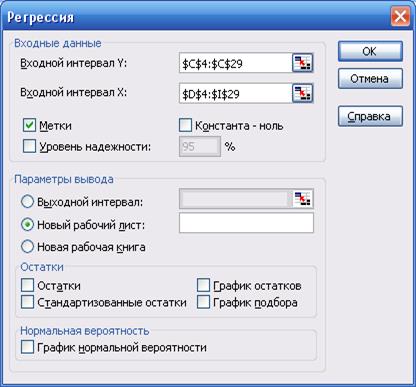
рис. 2. Панель регрессионного анализа модели Y(X1, X2, X3, X4, X5, X6)

Таблица 2

Результаты регрессионного анализа модели Y(X1, X2, X3, X4, X5, X6)

Регрессионная статистика

Множественный R

0,98198162

R-квадрат

0,964287903

Нормированный R-квадрат

0,95238387

Стандартная ошибка

0,022104009

Наблюдения

25

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

6

0,23746847

0,039578078

81,00514774

4,86777E-12

Остаток

18

0,00879457

0,000488587

Итого

24

0,24626304

Уравнение регрессии

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-0,636271776

0,154851455

-4,108917011

0,000659017

X1

-0,000475358

0,000227659

-2,088028273

0,051277788

X2

0,001308341

0,001462331

0,894695276

0,382758026

X3

-0,001409251

0,001234667

-1,141401564

0,268660942

X4

0,000148682

0,001391523

0,106848061

0,916091389

X5

4,32269E-05

2,04475E-05

2,114043412

0,048729432

X6

0,018535201

0,001590436

11,65416465

8,06885E-10

3. По результатам проверки статистической значимости коэффициентов уравнения регрессии, проведенной в предыдущем пункте, строим новую регрессионную модель, содержащую только информативные факторы, к которым относятся:

·        факторы, коэффициенты при которых статистически значимы;

·        факторы, у коэффициентов которых t‑статистика превышает по модулю единицу (другими словами, абсолютная величина коэффициента больше его стандартной ошибки).

Сначала, проверим статистическую значимость уравнения регрессии. Табличное значение F-критерия Фишера можно определить с помощью встроенной функции  EXCEL «FРАСПОБР», которая имеет следующий синтаксис:

=FРАСПОБР(«Уровень значимости a»;«dfрег»;«dfост»)

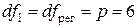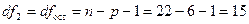         Для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии)  (где p=6 — число факторов в модели) и знаменателя (остатка)  табличное значение F-критерия Фишера составляет Fтабл=2,60.

         Видно, что расчетное значение F-статистики Фишера

 

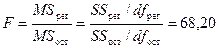
превышает табличное (см. «F» в табл. 2), что свидетельствует о статистической значимости уравнения регрессии в целом. На этот же факт указывает и то, что вероятность случайного формирования уравнения регрессии в том виде, в каком оно имеется, составляет 3,20×10-6 (см. «Значимость F» в табл. 2), что ниже допустимого уровня значимости a=0,05.

         Проверим статистическую значимость коэффициентов уравнения регрессии при факторах Х1, Х2, …, Х6 с помощью t-критерия Стьюдента:

.

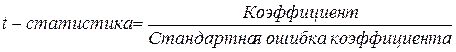         Табличное значение t-критерия Стьюдента можно определить с помощью встроенной функции  EXCEL «СТЬЮДРАСПОБР»:

=СТЬЮДРАСПОБР(«Уровень значимости a»;«dfост»)

         Для уровня значимости a=0,05 и числа степеней свободы остатка df=dfост=15 табличное значение t-критерия Стьюдента составляет 2,131. Анализ данных в табл. 2 показывает, что табличное значение t‑критерия Стьюдента превышают по абсолютной величине t-статистики коэффициентов при факторах Х5, Х6, и эти коэффициенты признаются статистически значимыми. На этот же факт указывают и значения вероятности случайного формирования коэффициентов, которые ниже допустимого уровня значимости a=0,05 (см. «P-Значение» в табл. 2).

         Что касается факторов Х1, Х2, Х3 и Х4 (в табл. 2), то t‑статистики их коэффициентов меньше по абсолютной величине табличного значения t-критерия Стьюдента, а «P-Значение» выше уровня значимости a=0,05. Таким образом эти коэффициенты не являются статистически значимыми.

По результатам проверки статистической значимости коэффициентов уравнения регрессии Y=f(Х1 X2, X3, X4, X5, X6), проведенной выше, строим новую регрессионную модель, содержащую только информативные факторы. Такими факторами будем считать либо факторы, коэффициенты при которых статистически значимы, либо факторы, у коэффициентов которых t‑статистика превышает по абсолютной величине единицу (другими словами, абсолютная величина коэффициента больше его стандартной ошибки). К первой группе относятся факторы Х1, Х6, ко второй — фактор X5. Факторы X2, X3, X4 исключаются из рассмотрения как неинформативные (÷tb5ç<1), и окончательно регрессионная модель будет содержать факторы X1, X5, X6.

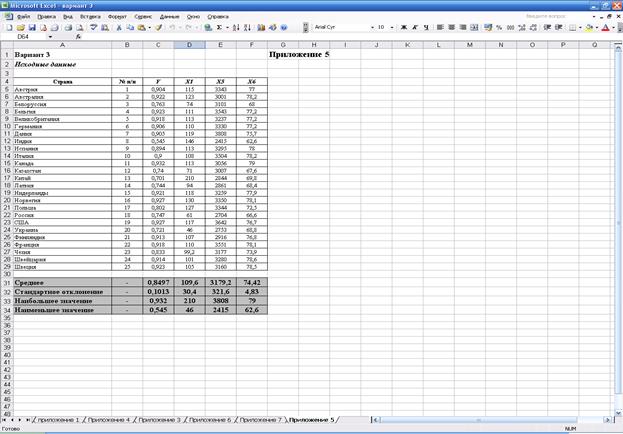
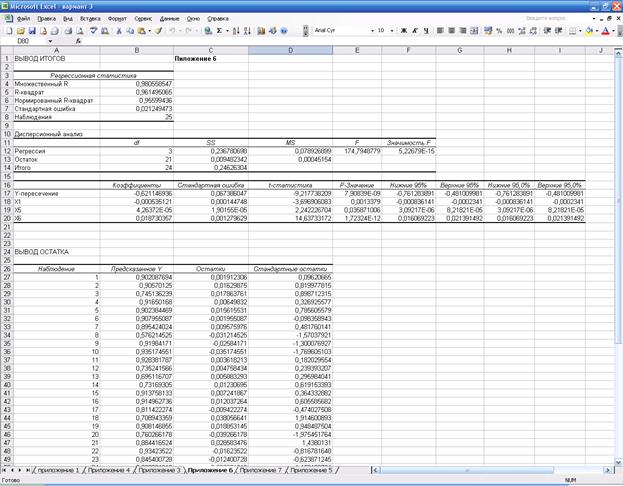
         Для построения уравнения регрессии Y=f(X1, X5, X6) скопируем на чистый рабочий лист  EXCEL значения переменных Y, X1, X5, X6 (прил. 5). Проводим регрессионный анализ (рис. 3). Его результаты приведены в прил. 6 и перенесены в табл.3. Само уравнение регрессии имеет вид:

.

        

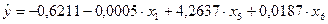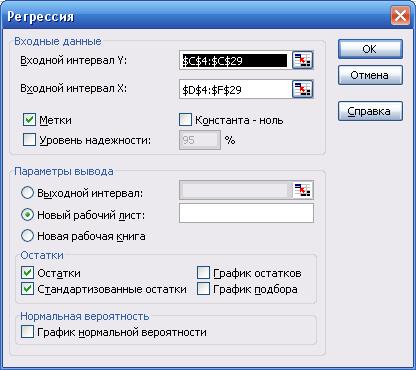
рис.3. Панель регрессионного анализа модели Y=f(X1,  X5, X6)

Таблица 3

Результаты регрессионного анализа модели Y=f(X1, X5, X6)

Регрессионная статистика

Множественный R

0,980558547

R-квадрат

0,961495065

Нормированный R-квадрат

0,95599436

Стандартная ошибка

0,021249473

Наблюдения

25

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

3

0,236780698

0,078926899

174,7948779

5,22679E-15

Остаток

21

0,009482342

0,00045154

Итого

24

0,24626304

Уравнение регрессии

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-0,621146936

0,067386047

-9,217738209

7,90839E-09

X1

-0,000535121

0,000144748

-3,696906083

0,0013379

X5

4,26372E-05

1,90155E-05

2,242226704

0,035871006

X6

0,018730357

0,001279629

14,63733172

1,72324E-12

         Уравнение регрессии статистически значимо в целом. Вероятность его случайного формирования ниже допустимого уровня значимости a=0,05 (см. «Значимость F» в табл. 3).

         Статистически значимыми являются коэффициент при факторе Х1: вероятность его случайного формирования ниже допустимого уровня значимости a=0,05 (см. «P-Значение» в табл. 3). Это свидетельствует о существенном влиянии изменения данных фактора на изменение годовой прибыли Y.

         Коэффициенты при факторах Х5,Х6 (выделены в табл. 3 заливкой и жирным шрифом) не является статистически значимыми. Однако эти факторы можно считать информативным, так как t‑статистика их коэффициенты превышают по абсолютной величине единицу, хотя к дальнейшим выводам относительно факторов Х5,Х6 следует относиться с некоторой осторожностью.

 

4. Оценим качество и точность последнего уравнения регрессии, используя некоторые статистические характеристики, полученные в ходе регрессионного анализа (см. «Регрессионную статистику» в табл. 3):

·        множественный коэффициент детерминации

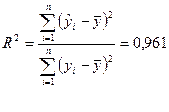
показывает, что регрессионная модель объясняет 96,1 % зависимости индекса человеческого развития Y, причем эта вариация обусловлена изменением включенных в модель регрессии факторов X1, X5 и X6;

·        стандартная ошибка регрессии

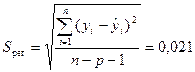 тыс. чел.

показывает, что предсказанные уравнением регрессии значения зависимости индекса человеческого развития Y отличаются от фактических значений в среднем на 0,021 тыс. человек.

         Средняя относительная ошибка аппроксимации определяется по приближенной формуле:

 %,

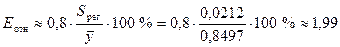где 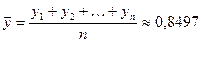 тыс. руб. — среднее значение зависимости индекса человеческого развития (определено с помощью встроенной функции «СРЗНАЧ»; прил. 1).

         Еотн показывает, что предсказанные уравнением регрессии значения зависимости индекса человечесого развития Y отличаются от фактических значений в среднем на 1,99 %. Модель имеет высокую точность (при 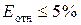 — точность модели высокая, при 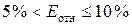 — хорошая, при  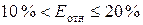— удовлетворительная, при 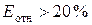 — неудовлетворительная).

 

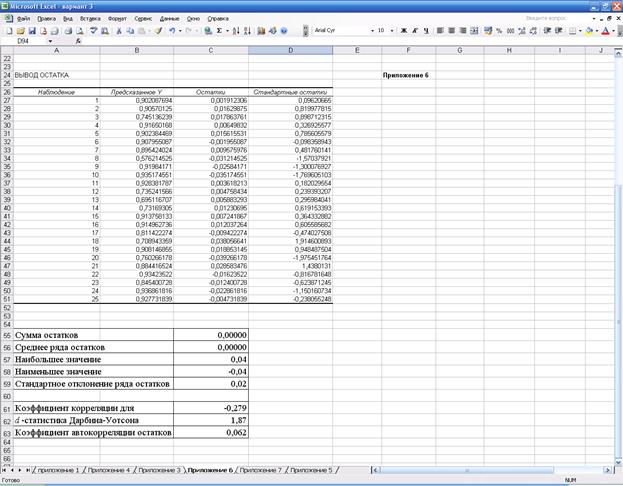
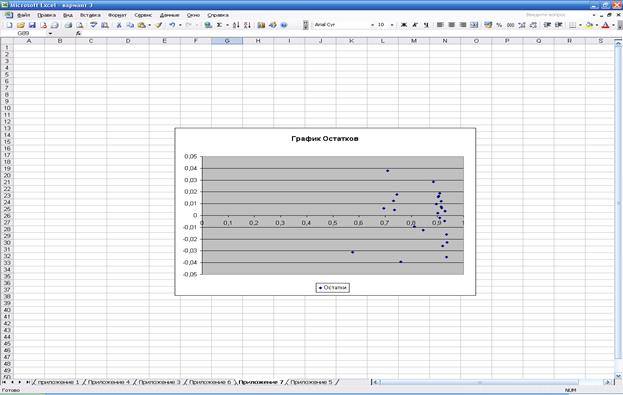
5. Построим график остатков ei от предсказанных уравнением регрессии значений результата 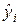 (i=1, 2, …, n) с помощью диаграммы  EXCEL: меню «Вставка» ® «Диаграмма…» ® «Точечная» (рис. 4). Предварительно в «Выводе остатка» в прил. 6 выделяются блоки ячеек «Предсказанное Y» и «Остатки» вместе с заголовками. График остатков приведен в прил. 7.

 

 

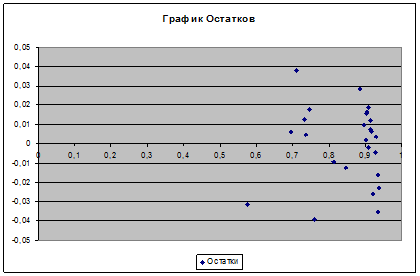
рис. 4. Построение графика остатков

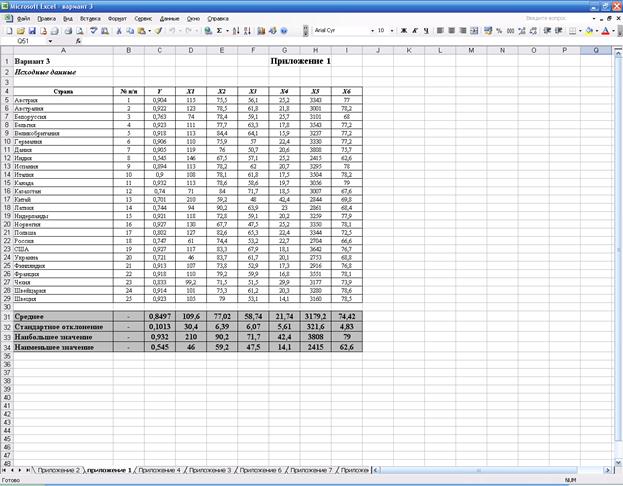
Для экономической интерпретации коэффициентов уравнения регрессии сведем в таблицу средние значения и стандартные отклонения переменных в исходных данных (табл. 4). Средние значения были определены с помощью встроенной функции «СРЗНАЧ», стандартные отклонения — с помощью встроенной функции «СТАНДОТКЛОН» (см. прил. 1).

Таблица 4

Средние значения и стандартные отклонения используемых переменных

Переменная

Y

X1

X5

X6

Среднее

0,8497

77,02

58,74

21,74

Стандартное отклонение

0,1013

6,39

6,07

5,61

1) Фактор X1 (ВВП 1997 г., % к 1990 г.)

         Значение коэффициента b1=(-0,00053512) показывает, что рост  размеров ВВП на 1%  приводит к снижению индекса человеческого развития в  среднем на -0,000535121.

         Средний коэффициент эластичности фактора X1 имеет значение

.

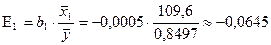         Он показывает, что при увеличении размеров ВВП на 1 %  зависимость индекса человеческого развития уменьшается в среднем на 0,06545 %.

2) Фактор X5 (суточная калорийность питания населения, ккал на душу населения)

         Значение коэффициента b5=0,00004 показывает, что рост суточного питания на душу населения на 1 ккал. приводит к увеличению индекса человеческого развития в среднем на 0,00004.

         Средний коэффициент эластичности фактора X5 имеет значение

.

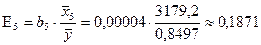         Он показывает, что при увеличении суточной каллорийности питания населения на 1 ккал. на душу населения зависимость индекса человеского развития увеличивается в среднем на 0,1871 %.

3) Фактор X6 (ожидаямая продолжительность жизни при рождении в 1997 г., число лет)

         Значение коэффициента b6=0,018730357 показывает, что рост годовой ожидаймости продолжительности жини при рождении на 1 год приводит к увелечению индекса человеческого развития в среднем на 0,018730357.

         Средний коэффициент эластичности фактора X6 имеет значение

.

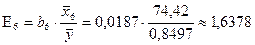         Он показывает, что при увеличении ожидаймой продолжительности жизни при рождении в 1997 году зависимость индекса человеческого развития увеличивается в среднем на 1,6378 %.

                  Сравним между собой силу влияния факторов, включенных в регрессионную модель, на зависимость индекса человеческого развития, для чего определим их бета–коэффициенты:

;

;

.

.

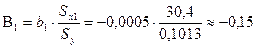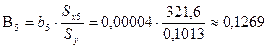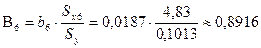         Сравнивая по абсолютной величине значения бета–коэффициентов, можно сделать вывод о том, что на зависимость индекса человеческого развития Y сильнее всего влияет ожидаемая продолжительность жизни при рождении Х6, далее по степени влияния следуют суточная калорийность питания населения  Х5 и ВВП  X1.

         Определим дельта–коэффициенты факторов:

;

;

,

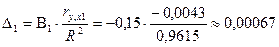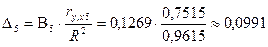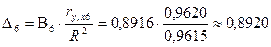где ry,x1=(-0,00434); ry,x5=0,75145; ry,x6=0,962033— коэффициенты корреляции между парами переменных Y–X1, Y–X5 и Y–X6 соответственно (см. табл. 1); R2=0,961495065— множественный коэффициент детерминации (см. табл. 3).

         Сумма дельта–коэффициентов факторов, включенных в модель, должна быть равна единице. Небольшое неравенство может быть вызвано погрешностями промежуточных округлений.

         Таким образом, в суммарной зависимости индекса человеческого развития Y всех факторов, включенных в модель, доля влияния ВВП X1 составляет 0,067 %, суточная каллорийность питания населения Х5 — 9,91 %, ожидаймой продолжительности жизни при рождении Х6 — 89,2 %. Поэтому произведя расчеты можем сказать, что выполняются четыре из пяти предпосылок обычного метода наименьших квадратов. ( Тоесть, 1) Случайный характер остатков. Визуальный анализ графика остатков (см. прил. 7) не выявляет в них какой-либо явной закономерности.

         2) Нулевая средняя величина остатков. Данная предпосылка всегда выполняется для линейных моделей со свободным коэффициентом b0, параметры которых оцениваются обычным методом наименьших квадратов.

3) Зависимость между дисперсией случайного члена и объясняющей переменной (гетероскедастичность). Статистическая гипотеза об одинаковой дисперсии остатков отклоняется на уровне значимости a=0,05. Положительное значение коэффициента корреляции указывает на то, что индекс человеческого развития  Y  с большим ВВП 1997 г., % к 1990 г. имеет существенно большую вариацию.    Невыполнение предпосылки об одинаковой дисперсии остатков свидетельствует о том, что данная модель не вполне адекватна, а оценки параметров модели обычным методом наименьших квадратов могут не быть эффективными, т.е. их дисперсии могут не быть наименьшими.

4) Отсутствие автокорреляции остатков. Выполнение данной предпосылки проверяем методом Дарбина–Уотсона. Предварительно ряд остатков упорядочивается в зависимости от последовательно возрастающих значений Y, предсказанных уравнением регрессии. Для этой цели в «Выводе остатка» прил. 6 выделяется любая ячейка в столбце «Предсказанное Y», и на панели инструментов нажимается кнопка «» («Сортировка по возрастанию»).

         Для расчета d‑статистики в  EXCEL используется выражение, составленное из встроенных функций:

=СУММКВРАЗН(«Остатки 2, …, n»; «Остатки 1, …, n–1»)/СУММКВ(«Остатки 1, …, n»)

         d‑статистика имеет значение

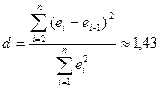 (см. прил. 6).

         Критические значения d‑статистики для числа наблюдений n=20, числа факторов p=3 и уровня значимости a=0,05 составляют: d1=1,00; d2=1,68.

         Так как выполняется условие

,

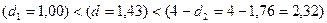статистическая гипотеза об отсутствии автокорреляции в остатках не отклоняется на уровне значимости a=0,05.

         Проверим отсутствие автокорреляции в остатках также и по коэффициенту автокорреляции остатков первого порядка, для расчета которого использовалось выражение, составленное из встроенных функций  EXCEL:

=СУММПРОИЗВ(«Остатки 2, …, n»; «Остатки 1, …, n–1»)/СУММКВ(«Остатки 1, …,n»)

         Ряд остатков упорядочен в той же самой последовательности, что и при расчете d‑статистики. Коэффициент автокорреляции остатков первого порядка равен

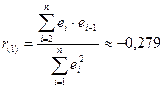 (см. прил. 6).

         Критическое значение коэффициента автокорреляции для числа наблюдений n=20 и уровня значимости a=0,05 составляет r(1)кр=0,423. Так как коэффициент автокорреляции остатков первого порядка не превышает по абсолютной величине критическое значение, то это еще раз указывает на отсутствие автокорреляции в остатках.

         5) Нормальный закон распределения остатков. Выполнение этой предпосылки проверяем с помощью R/S-критерия

,

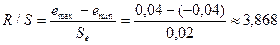где emax=0,04; emin=(–0,04) — наибольший и наименьший остатки соответственно (определялись с помощью встроенных функций «МАКС» и «МИН»); 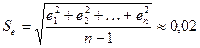 — стандартное отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН») (см. прил. 6).

         Критические границы R/S-критерия для числа наблюдений n=20 и уровня значимости a=0,05 имеют значения: (R/S)1=3,18 и (R/S)2=4,49.

         Так расчетное значение R/S-критерия попадает в интервал между критическими границами, то это означает, что статистическая гипотеза о нормальном законе распределения остатков не отклоняется на уровне значимости a=0,05.)

Все это говорит о том, что регрессионная модель не вполне адекватна исследуемому экономическому явлению, и использовать ее для целей анализа и прогнозирования индекса человеческого развития следует с некоторой осторожностью.

6. Рассчитаем прогнозное значение индекса человеческого развития, если прогнозные значения факторов составят 75 % от своих максимальных значений в исходных данных. Максимальные значения факторов были определены с помощью встроенной функции «МАКС» (см. прил. 1). Прогнозные значения рассчитываются только для количественных факторов X1, X5, X6:

·        фактор Х1: ;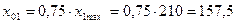

·        фактор Х5: ;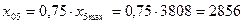

·        фактор Х6: .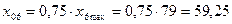

        

Среднее прогнозируемое значение (точечный прогноз) составляет:

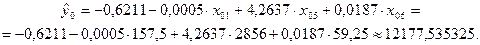
Стандартная ошибка прогноза фактического значения годовой прибыли y0 рассчитывается по формуле

                  

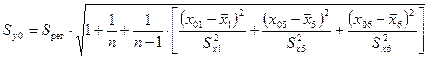
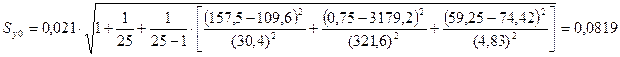
         Построим интервальный прогноз фактического значения индекса человеческого развития y0 с доверительной вероятностью g=0,8. Доверительный интервал имеет вид:

,

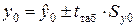где tтаб=1,323 — табличное значение t-критерия Стьюдента при уровне значимости 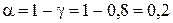 и числе степеней свободы 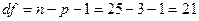 (p=3 — число факторов в модели) (см. Справочные таблицы, таблица 3).

         .

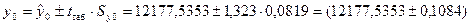         Таким образом, с вероятностью 80 % индекс человеческого развития при заданных значениях факторов будет находиться в интервале от 12177,4269 до 12177,6437.

                 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 1

ПРИЛОЖЕНИЕ 2

ПРИЛОЖЕНИЕ 3

ПРИЛОЖЕНИЕ 4

ПРИЛОЖЕНИЕ 5

ПРИЛОЖЕНИЕ 6

ПРИЛОЖЕНИЕ 7

[1]Специальный индекс человеческого развития, который объединяет три показателя (валовой внутренний продукт на душу населения, грамотность и продолжительность предстоящей жизни) и дает обобщенную оценку человеческого прогресса. Впервые данный показатель был предложен в 1990 г. группой исследователей Программы развития ООН.

[2]Для копирования снимка окна в буфер обмена данных WINDOWS используется комбинация клавиш Alt+Print Screen (на некоторых клавиатурах — Alt+PrtSc).