Министерство образования и науки
Российской Федерации
Федеральное агентство по образованию
ГОУ ВПО
Всероссийский заочный
финансово-экономический институт
КОНТРОЛЬНАЯ РАБОТА
по дисциплине « экономико-математические методы и прикладные модели»
Вариант №2
Выполнила:
Факультет: финансово-кредитный
Специальность: финансы и кредит.
Группа: 0604(договор, вечер) III курс
Зачетная книжка:
Преподаватель: Князева И.В.
Калуга 2007
ОГЛАВЛЕНИЕ
Задача 1. 3
Задача 2. 4
Задача 3. 8
Задача 4. 9
Задача 1
Решить графическим методом типовую
задачу оптимизации
Совхоз для кормления животных использует два
вида корма. В дневном рационе животного должно содержаться не менее 6 единиц
питательного вещества А и не менее 12 единиц питательного вещества В. Какое
количество корма надо расходовать ежедневно на одно животное, чтобы затраты
были минимальными? Использовать данные таблицы.
|
Питатательное
вещество
|
Количество
питательных веществ в 1 кг
корма
|
|
1
|
2
|
|
А
|
2
|
1
|
|
В
|
2
|
4
|
|
Цена 1 кг корма, тыс. руб.
|
0,2
|
0,3
|
Построить экономико-математическую
модель задачи, дать необходимые
комментарии к ее элементам и получить решение графическим методом. Что
произойдет, если решать задачу на максимум, и почему?
Решение:
1. сформулируем целевую функцию: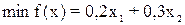
2. сформулируем функциональные ограничения для целевой
функции:
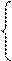
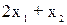 ≥6
≥6
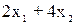 ≥12
≥12
х1,2≥0
3. найдем значения х1 и х2
методом Гаусса:
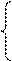

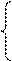
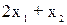 ≥6;
≥6; 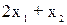 ≥6;
≥6;
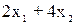 ≥12. 3х2≥6; х2=2; х1=2 ;
≥12. 3х2≥6; х2=2; х1=2 ;
4. Вычислим значение целевой функции в
точке пересечения (2;2):
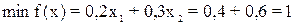
5. график изобразим на рисунке 1:
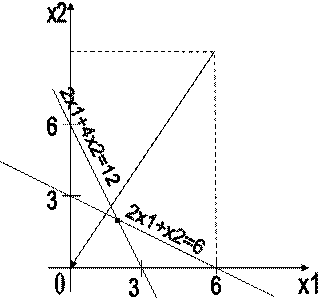
Рис. 1. График решения задачи.
Ответ: 1. 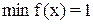 и достигается при х1=2;
х2=2.
и достигается при х1=2;
х2=2.
2. Если задачу решать на максимум, то целевая функция 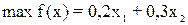 неограниченная и ЗЛП
не имеет решения,
неограниченная и ЗЛП
не имеет решения, 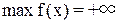 .
.
Задача 2
Использовать аппарат теории
двойственности для экономико-математического анализа оптимального плана задачи
линейного программирования
Для изготовления четырех видов
продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены
реализации единицы, каждого вида продукции приведены в таблице.
|
Тип сырья
|
Нормы расхода сырья на одно изделие
|
Запасы сырья
|
|
А
|
Б
|
В
|
Г
|
|
I
|
1
|
0
|
2
|
1
|
180
|
|
II
|
0
|
1
|
3
|
2
|
210
|
|
III
|
4
|
2
|
0
|
4
|
800
|
|
Цена изделия
|
9
|
6
|
4
|
7
|
|
Решение:
1. Сформулировать прямую оптимизационную
задачу на максимум выручки от реализации готовой продукции, получить
оптимальный план выпуска продукции.
2. Сформулировать двойственную задачу и
найти ее оптимальный план с помощью теорем двойственности.
3. Пояснить нулевые значения переменных
в оптимальном плане.
4. На основе свойств двойственных оценок
и теорем двойственности:
Ø 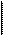 проанализировать использование ресурсов в оптимальном плане
исходной задачи;
проанализировать использование ресурсов в оптимальном плане
исходной задачи;
Ø определить, как изменятся выручка и
план выпуска продукции при увеличении запасов сырья II и III видов на 120 и
160 единиц соответственно и уменьшении на 60 единиц запасов сырья I вида;
Ø оценить целесообразность включения в
план изделия Д ценой 12 единиц, на изготовление которого расходуется по две
единицы каждого вида сырья.
1. Сформулируем целевую функцию: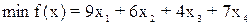
сформулируем функциональные ограничения для целевой
функции:
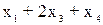 ≤180
≤180
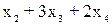 ≤210
≤210
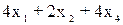 ≤800
≤800
х1,2,3,4≥0
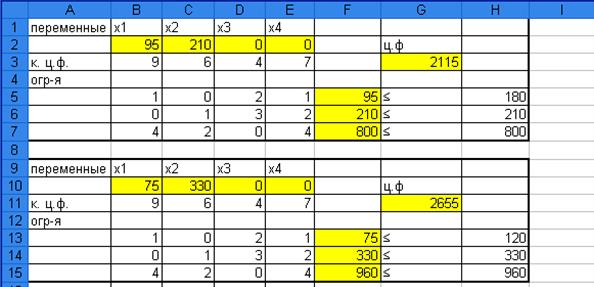
С помощью надстройки Excel « Поиск решения» (рис.2.) найдем оптимальный
план задачи (значения 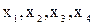 , и значение функции
, и значение функции 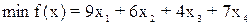 ).
).
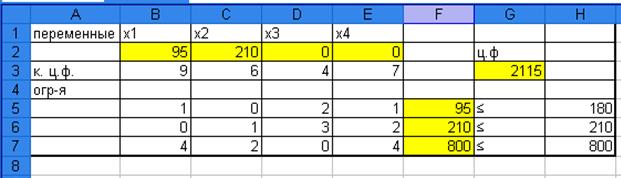
Рис. 2. Решение с помощью надстройки Excel « Поиск решения».
Подставим найденный оптимальный план
в систему функциональных ограничений: столбец «F» (рис 2), поскольку второе и третье
ограничения содержат знаки равно между правой и левой частью переменные целевой
y1 и y2 не будут равны нулю, и поскольку первое ограничение
содержит знак неравенства, по второй теореме двойственности y1=0.
2. Сформулировать двойственную задачу и
найти ее оптимальный план с помощью теорем двойственности.
Minφ(x)= 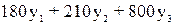
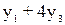 ≥9
≥9
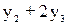 ≥6
≥6
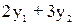 ≥4
≥4
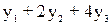 ≥7
≥7
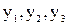 ≥0
≥0
По второй части второй
теоремы двойственности, поскольку y1 и y2 >0 второе и третье ограничения содержат знаки равно между
правой и левой частью, т.е. правомерно решить систему уравнений:
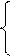
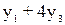 =9,
=9,
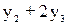 =6; y1=0; y2=1,5; y3=2,25.
=6; y1=0; y2=1,5; y3=2,25.
3. y1 = 0 – это самый не дефицитный ресурс,
а y3 = 2,25 – самый дефицитный.
4.
Для
анализа воспользуемся свойствами двойственных оценок:
Если увеличить запасы
второго сырья на 120 единиц, третьего
сырья на 160 единиц, и уменьшении первого сырья на 60 единиц, то выручка
увеличится на 700 единиц, а план выпуска продукции изменится.
|
Тип сырья
|
Запасы сырья
|
Увеличение запасов сырья (Х)
|
Ресурсы (Y)
|
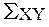
|
|
1
|
180
|
-60
|
0
|
0
|
|
2
|
210
|
120
|
1,5
|
180
|
|
3
|
800
|
160
|
2,25
|
360
|
|
|
|
|
|
540
|
|
F(x)
|
2115
|
+
|
540
|
2655
|
Из таблицы видно, что при увеличении запасов сырья (1-го на
-60, 2-го на 120, 3-го на 160) целевая функция увеличилась на 540 ед.
max
f(x) = 120y1+310y2+960y3=2655
Отчет
по устойчивости
|
|
|
|
|
|
|
|
|
|
Изменяемые
ячейки
|
|
|
|
|
|
|
|
|
Результ.
|
Нормир.
|
Целевой
|
Допустимое
|
Допустимое
|
|
|
Ячейка
|
Имя
|
значение
|
стоимость
|
Коэффициент
|
Увеличение
|
Уменьшение
|
|
|
$B$10
|
x1
|
75
|
0
|
9
|
0,333333334
|
9
|
|
|
$C$10
|
x2
|
330
|
0
|
6
|
1E+30
|
0,166666667
|
|
|
$D$10
|
х3
|
0
|
-0,500000001
|
3,999999999
|
0,500000001
|
1E+30
|
|
|
$E$10
|
х4
|
0
|
-5
|
7,000000001
|
5
|
1E+30
|
|
|
|
|
|
|
|
|
|
|
Ограничения
|
|
|
|
|
|
|
|
|
|
Результ.
|
Теневая
|
Ограничение
|
Допустимое
|
Допустимое
|
|
|
Ячейка
|
Имя
|
значение
|
Цена
|
Правая
часть
|
Увеличение
|
Уменьшение
|
|
|
$F$13
|
|
75
|
0
|
120
|
1E+30
|
45
|
|
|
$F$14
|
|
330
|
1,5
|
330
|
150
|
90
|
|
|
$F$15
|
|
960
|
2,25
|
960
|
180
|
300
|
Из отчета видно, что
запасы дефицитных ресурсов, 2-го и 3-го видов сырья могут быть, как уменьшены,
так и увеличены. Увеличение запаса
1-го ресурса на план
выпуска продукции не влияет. Новый план
выпуска составляет 75 изделий первого вида и 330 изделий второго вида.
Изменение общей стоимости продукции на 540 ед.(2655-2115=540)получено за счет
уменьшения плана выпуска на 20ед. продукции первого вида по цене 9 ед.
(9*(75-95)=-180 ед.) и увеличении на 120 ед. продукции второго вида по цене 6
ед. (6*(330-210)=720 ед.).
Ø С помощью оценок двойственности можно
понять эффектно или не эффектно было бы производить изделие Д ценой 12 единиц,
на изготовление которого расходуется по две единицы каждого вида сырья.
|
Тип
сырья
|
Нормы
расхода сырья на одно изделие (Д)
|
Оценки
ресурсов
|
|
I
|
2
|
0
|
|
II
|
2
|
1,5
|
|
III
|
2
|
2,25
|
|
Цена
изделия
|
12
|
|
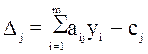 =2*0+2*1,5+2*2,25-12=-4,5 < 0, это значит что изделие выгодно для включения в план, т.к. затраты на
его изготовление покрываются полученной прибылью.
=2*0+2*1,5+2*2,25-12=-4,5 < 0, это значит что изделие выгодно для включения в план, т.к. затраты на
его изготовление покрываются полученной прибылью.
Задача 3
Используя балансовый метод
планирования и модель Леонтьева, построить баланс производства и распределения
продукции предприятий.
Промышленная группа предприятий (холдинг)
выпускает продукцию трех видов, при этом каждое из трех предприятий группы
специализируется на выпуске продукции одного вида: первое предприятие
специализируется на выпуске; продукции первого вида, второе предприятие —
продукции второго вида; третье предприятие — продукции третьего вида. Часть
выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее
потребление), остальная часть поставляется за его пределы (внешним
потребителям, является конечным продуктом).
Специалистами управляющей компании
получены экономические оценки аij (i=1,2, 3; j= 1, 2, 3) элементов технологической
матрицы A (норм расхода, коэффициентов прямых материальных затрат) и элементов уi вектора конечной продукции Y.
Требуется:
1. Проверить продуктивность
технологической матрицы
A = (аij) (матрицы коэффициентов прямых
материальных затрат).
2. Построить баланс (заполнить таблицу)
производства и
распределения продукции предприятий холдинга.
|
Предприятия
(виды продукции)
|
Коэффициенты
прямых затрат аij
|
Конечный
продукт Y
|
|
1
|
2
|
3
|
|
1
|
0,0
|
0,1
|
0,2
|
180
|
|
2
|
0,1
|
0,2
|
0,1
|
200
|
|
3
|
0,2
|
0,1
|
0,2
|
200
|
Решение:
Ø Опишем модель Леонтьева в общем виде
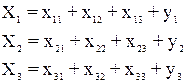
Ø Отдельные элементы матрицы прямых
материальных затрат вычисляются по формуле:
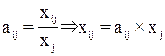
Ø С учетом представленных формул модель
Леонтьева для решения данной задачи такова:
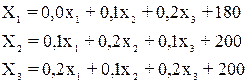
|
|
|
|
|
|
|
|
|
|
|
A
|
0
|
0,1
|
0,2
|
|
E
|
1
|
0
|
0
|
|
0,1
|
0,2
|
0,1
|
|
0
|
1
|
0
|
|
0,2
|
0,1
|
0,2
|
|
0
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
|
(E-A)
|
1
|
-0,1
|
-0,2
|
|
|
|
|
|
|
-0,1
|
0,8
|
-0,1
|
|
|
|
|
|
|
-0,2
|
-0,1
|
0,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B
|
1,075085
|
0,170648
|
0,290102
|
|
Y
|
180
|
|
|
|
0,170648
|
1,296928
|
0,204778
|
|
200
|
|
|
|
0,290102
|
0,204778
|
1,348123
|
|
200
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X
|
285,6655
|
|
|
|
|
|
|
|
|
331,058
|
|
|
|
|
|
|
|
|
362,7986
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xij
|
0
|
33,1058
|
72,55973
|
|
|
|
|
|
|
28,56655
|
66,2116
|
36,27986
|
|
|
|
|
|
|
57,13311
|
33,1058
|
72,55973
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производящие
отрасли
|
потребляющие
отрасли
|
Конечный
продукт
|
Валовый продукт
|
|
|
|
|
1
|
2
|
3
|
|
|
|
|
1
|
0
|
33,1058
|
72,55973
|
180
|
285,6655
|
|
|
|
|
2
|
28,56655
|
66,2116
|
36,27986
|
200
|
331,058
|
|
|
|
|
3
|
57,13311
|
33,1058
|
72,55973
|
200
|
362,7986
|
|
|
|
|
Условно
чистая продукция
|
199,9659
|
198,6348
|
181,3993
|
580
|
|
|
|
|
|
валовый продукт
|
285,6655
|
331,058
|
362,7986
|
|
979,5222
|
|
|
|
Задача 4
Исследовать динамику экономического
показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос
7(0 (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t)
этого показателя приведен ниже в таблице.
|
Номер варианта
|
Номер наблюдения (t = 1, 2, ...,9)
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
43
|
47
|
50
|
48
|
54
|
57
|
61
|
59
|
65
|
Требуется:
1. Проверить наличие аномальных наблюдений.
2. Построить линейную модель Ŷ(t) = a0+а1t, параметры которой оценить МНК (Ŷ(t)) —
расчетные, смоделированные значения временного ряда.
3. Построить адаптивную модель Брауна Ŷ(t) =a0+a1k с параметром
сглаживания α = 0,4 и α = 0,7; выбрать лучшее значение параметра
сглаживания.
4. Оценить адекватность построенных моделей, используя свойства
независимости остаточной компоненты, случайности и соответствия нормальному
закону распределения (при использовании R/S-критерия взять
табулированные границы 2,7—3,7).
5. Оценить точность моделей на основе использования
средней относительной ошибки аппроксимации.
6. По двум построенным моделям осуществить прогноз спроса
на следующие две недели (доверительный интервал прогноза рассчитать при
доверительной вероятности p = 70%).
7. Фактические значения показателя, результаты
моделирования и прогнозирования представить графически.
Вычисления
провести с одним знаком в дробной части. Основные промежуточные результаты
вычислений представить в таблицах (при использовании компьютера представить
соответствующие листинги с комментариями).
Решение.
1. Проверяем наличие аномальных наблюдений методом
Ирвина:
Вычисляется число 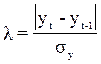 ;
;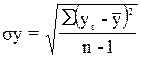 ;
;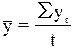 ;
;
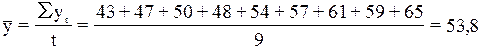 ;
;
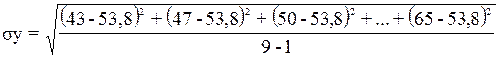 =7,29;
=7,29;
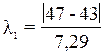 =0,55;…
=0,55;…
Значения λn представлены в таблице:
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
λn
|
0,55
|
0,41
|
0,27
|
0,82
|
0,41
|
0,55
|
0,27
|
0,82
|
Все значения λn
расчетные
меньше чем табличное λ = 1,5, следовательно аномальных явлений нет.
2. Рассчитаем начальные параметры модели
используя метод наименьших квадратов. Суть метода наименьших квадратов при
исследовании модели Ŷ(t) = a0+а1t необходимо найти такие значения a0
и а1 , которые минимизируют сумму квадратов отклонений расчетных
значений от наблюдаемых: 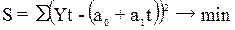 . Чтобы получить выражение для вычисления а0 и а1
и найти min S от
двух переменных, необходимо производные этой функции по каждой переменной
приравнять к нулю. В рамках решения полученной системы уравнений получим
следующие выражения для а0 и а1:
. Чтобы получить выражение для вычисления а0 и а1
и найти min S от
двух переменных, необходимо производные этой функции по каждой переменной
приравнять к нулю. В рамках решения полученной системы уравнений получим
следующие выражения для а0 и а1: 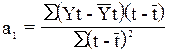 ;
;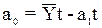 ;
;
|
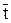 = =
|
5
|
|
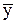 = =
|
53,8
|
3. Модель Брауна: 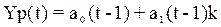 ;
;
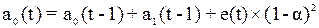 ;
;
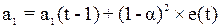 ;
;
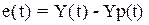 ;
;
Заполним таблицу расчетных
значений с параметром сглаживания 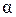 =0,4 (рис. 4.) с помощью Excel, мастер функций.
=0,4 (рис. 4.) с помощью Excel, мастер функций.
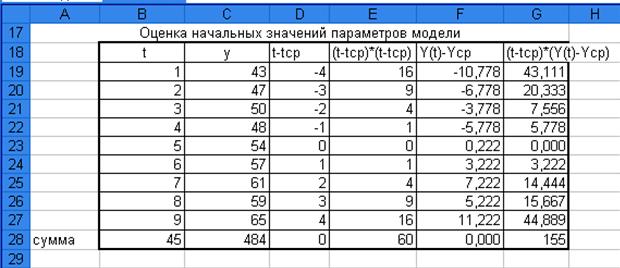
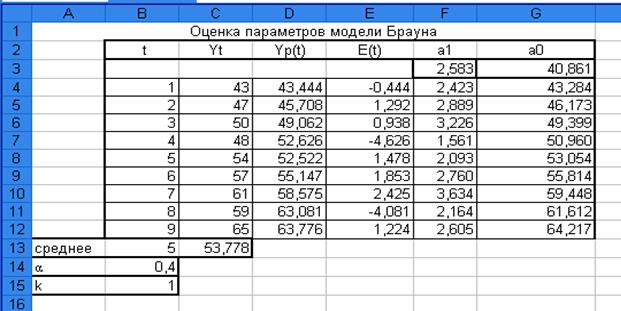 Рис. 4. Таблица расчетных значений с
параметром сглаживания
Рис. 4. Таблица расчетных значений с
параметром сглаживания 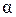 =0,4, вычисленная с помощью Excel, мастер функций.
=0,4, вычисленная с помощью Excel, мастер функций.
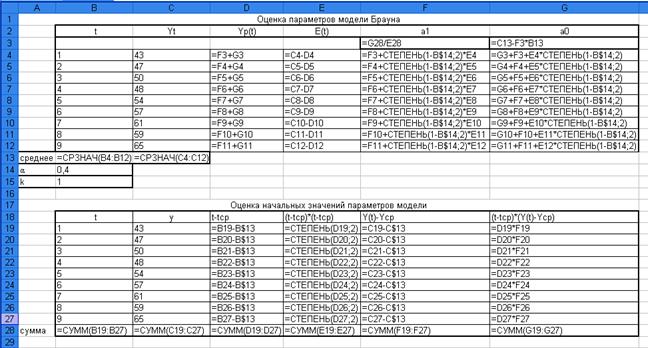 Рис. 5. Формульный шаблон решения
таблиц «Оценка начальных значений параметров модели» и «Оценка параметров модели Брауна».
Рис. 5. Формульный шаблон решения
таблиц «Оценка начальных значений параметров модели» и «Оценка параметров модели Брауна».
Заполним таблицу расчетных
значений с параметром сглаживания 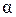 =0,7 (рис. 6) с помощью Excel, мастер функций.
=0,7 (рис. 6) с помощью Excel, мастер функций.
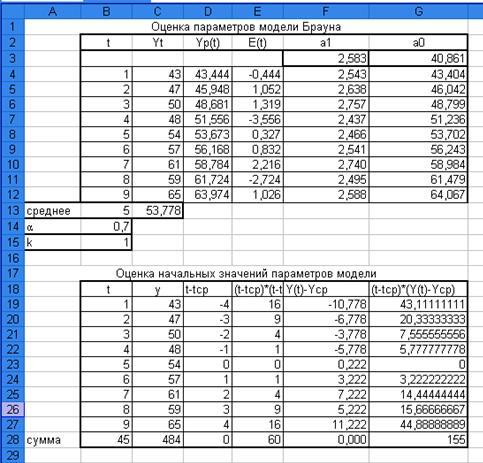
Рис. 6. Таблицу расчетных значений с параметром сглаживания 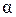 =0,7 с помощью Excel, мастер
функций.
=0,7 с помощью Excel, мастер
функций.
Формулы все те же, только с параметром сглаживания 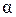 =0,7 (см. рис. 4.).
=0,7 (см. рис. 4.).
Выберем лучшее значение параметра
сглаживания, для этого сравним ошибки E(t): модель с параметром сглаживания 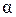 =0,4, E(t)=0,06, а модель с параметром
сглаживания
=0,4, E(t)=0,06, а модель с параметром
сглаживания 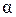 =0,7, E(t)=0,05, следовательно лучшее значение параметра сглаживания
=0,7, E(t)=0,05, следовательно лучшее значение параметра сглаживания 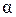 =0,7.
=0,7.
4.
Оценим адекватность построенных
моделей:
1.
Модель с параметром сглаживания 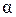 =0,4:
=0,4:
Проверку случайности уровней ряда остатков проведем на основе
критерия пиков (поворотных точек). Точки пиков отметим в столбце «F», рис. 7. ,их количество равно
четырем (р=4).
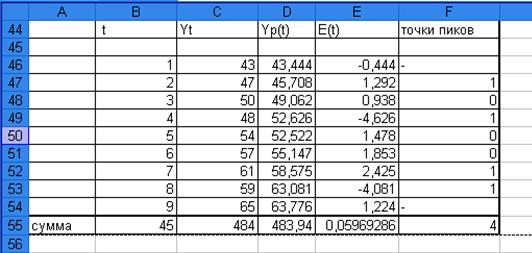
Рис. 7. Таблица: «Точки пиков».
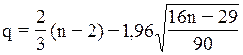
Правая часть неравенства p>q равняется в нашем случае двум, т.е.
это неравенство выполняется. Следовательно, свойство случайности ряда остатков
подтверждается.
Проведем проверку соответствия
остаточной последовательности нормальному закону распределения. Воспользуемся RS-критерием.
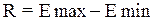 =2,425+4,626=7,051
=2,425+4,626=7,051
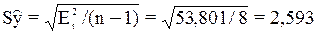
RS=R/S=7,051/2,593=2,72, это значение
попадает в интервал между нижней и верхней границами табличных значений данного
критерия (эти границы для n = 10 и уровня значимости α=
0,05 составляют соответственно 2,7 и 3,7). Это позволяет сделать вывод, что
свойство нормальности распределения выполняется.
Переходя к проверке равенства
(близости) нулю математического ожидания ряда остатков, заметим, что по результатам
вычислений в таблице (рис.7) это математическое ожидание равно 0,06: 9 = 0,007
и, следовательно, можно подтвердить выполнение данного свойства, не прибегая к
статистике Стьюдента.
Для проверки независимости уровней
ряда остатков (отсутствия автокорреляции) вычислим значение критерия Дарбина—Уотсона.
Расчеты по формуле 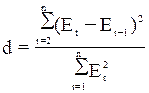 , представленные в столбцах «G,H,I» (рис. 8.)
, представленные в столбцах «G,H,I» (рис. 8.)
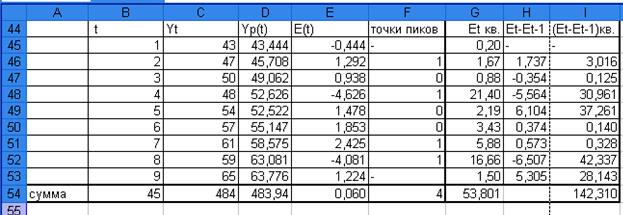
дают следующее значение этого
критерия: d = 142,310 : 53,8 = 2,65. Эта величина превышает 2, что
свидетельствует об отрицательной автокорреляции, поэтому критерий
Дарбина—Уотсона необходимо преобразовать: d' = 4-d = 4- 2,65 =1.35. Данное значение
сравниваем с двумя критическими табличными значениями критерия, которые для
линейной модели в нашем случае можно принять равными d1 =1,08 и d2
— 1,36. Так как расчетное значение попадает в интервал от d2 до 2, то делается вывод о
независимости уровней остаточной последовательности.
Из сказанного выше следует, что
остаточная последовательность удовлетворяет всем свойствам случайной компоненты
временного ряда, следовательно, построенная линейная модель является
адекватной.
2.
Модель с параметром сглаживания 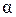 =0,7:
=0,7:
Проверку случайности уровней ряда остатков проведем на основе
критерия пиков (поворотных точек). Точки пиков отметим в столбце «F», рис. 9. ,их количество равно
четырем (р=4).
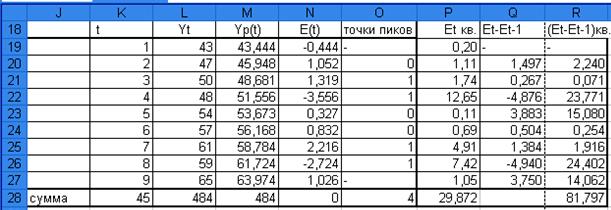
Рис. 9. Таблица: «Расчетные
значения».
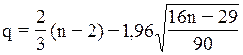
Правая часть неравенства p>q равняется в нашем случае двум, т.е.
это неравенство выполняется. Следовательно, свойство случайности ряда остатков
подтверждается.
Проведем проверку соответствия
остаточной последовательности нормальному закону распределения. Воспользуемся RS-критерием.
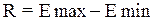 =2,216+3,556 =5,772
=2,216+3,556 =5,772
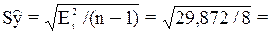 3,734
3,734
RS=R/S=5,772/3,734=1,546, это значение не попадает
в интервал между нижней и верхней границами табличных значений данного критерия
(эти границы для n= 10 и уровня значимости α= 0,05
составляют соответственно 2,7 и 3,7). Это позволяет сделать вывод, что свойство
нормальности распределения не выполняется.
Переходя к проверке равенства
(близости) нулю математического ожидания ряда остатков, заметим, что по результатам
вычислений в таблице (рис.7) это математическое ожидание равно 0,047: 9 = 0,005 и, следовательно, можно подтвердить выполнение
данного свойства, не прибегая к статистике Стьюдента.
Для проверки независимости уровней
ряда остатков (отсутствия автокорреляции) вычислим значение критерия Дарбина—Уотсона.
Расчеты по формуле 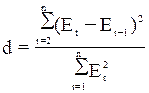 , представленные в столбцах «P,Q,R» (рис. 9.)
, представленные в столбцах «P,Q,R» (рис. 9.)
дают следующее значение этого
критерия: d = 81,797 : 29,872 = 2,738. Эта величина превышает 2, что
свидетельствует об отрицательной автокорреляции, поэтому критерий
Дарбина—Уотсона необходимо преобразовать: d' = 4-d = 4- 2,738 = 1,262. Данное значение сравниваем с двумя критическими
табличными значениями критерия, которые для линейной модели в нашем случае
можно принять равными d1 =1,08 и d2 — 1,36. Так как
расчетное значение попадает в интервал от d2 до 2, то делается вывод о
независимости уровней остаточной последовательности.
Из сказанного выше следует, что
остаточная последовательность удовлетворяет не всем свойствам случайной компоненты
временного ряда, следовательно, построенная линейная модель является не адекватной.
5. Для характеристики точности модели
воспользуемся показателем
средней относительной ошибки аппроксимации, который
рассчитывается по формуле:
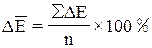 ;
; 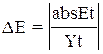 ;
; 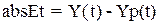 .
.
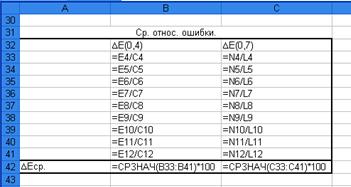
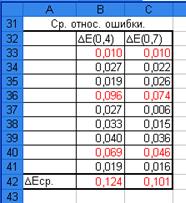
Рис. 10. Таблица в Excel «Средние относительные ошибки».
Средние
относительные ошибки не должны превышать 5%, в нашем случае ∆Е(0,4)=0,124<5% и
∆Е(0,7)=0,101<5%. Полученные значения средних относительных ошибок говорят
о достаточно высоком уровне точности обоих построенных моделей.
6.
По двум построенным моделям
осуществить прогноз спроса на следующие две недели (доверительный интервал
прогноза рассчитать при доверительной вероятности p = 70%).
I.
Модель с параметром сглаживания 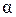 =0,4:
=0,4:
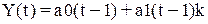
Y(t)пр=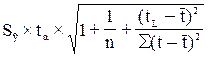 ;
; 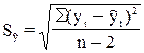 ;
;
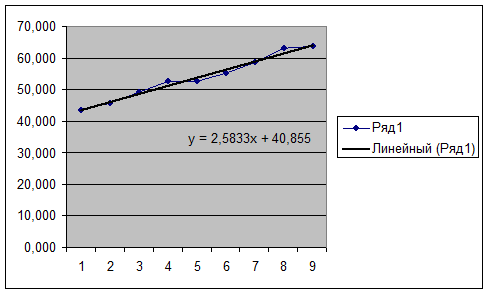
Рис. 11.
График и тренд расчетных значений
временного ряда.
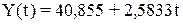 ;
;
Y(n+L)+U(L) – верхняя граница прогноза;
Y(n+L)-U(L) – нижняя граница прогноза;
P=70%; α=0,3; tα=1,05; t=10; L=1; n=9.
Результаты
вычислений представим в таблице 1.
|
Время (t)
|
Шаг
(L)
|
Точечный прогноз
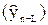
|
Доверительный интервал
прогноза
|
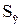
|
U
|
|
Нижняя граница.
|
Верхняя граница
|
|
10
|
1
|
66,69
|
61,45
|
71,92
|
2,772
|
5,237
|
|
11
|
2
|
69,27
|
64,03
|
74,51
|
|
5,237
|
II.
Модель с параметром сглаживания 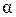 =0,7:
=0,7:

Y(t)пр=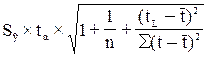 ;
; 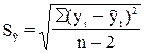 ;
;
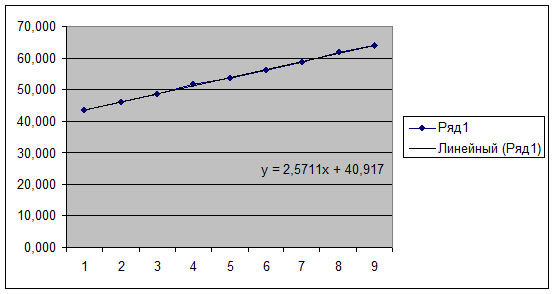
Рис. 12.
График и тренд расчетных значений
временного ряда.
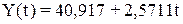 ;
;
Y(n+L)+U(L) – верхняя граница прогноза;
Y(n+L)-U(L) – нижняя граница прогноза;
P=70%; α=0,3; tα=1,05; t=11; L=2; n=9.
Результаты
вычислений представим в таблице 1.
|
Время (t)
|
Шаг
(L)
|
Точечный прогноз
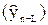
|
Доверительный интервал
прогноза
|
|
U
|
|
Нижняя граница.
|
Верхняя граница
|
|
10
|
1
|
66,628
|
59,78
|
73,48
|
4,267
|
6,850
|
|
11
|
2
|
69,199
|
62,56
|
75,83
|
|
6,636
|