Задача 3.

Определить силу прессования F, развиваемую гидравлическим прессом, у которого диаметр большего плунжера D, диаметр меньшего плунжера d. Больший плунжер расположен выше меньшего на величину H, рабочая жидкость Ж, усилие, приложенное к рукоятке, R.

                                          

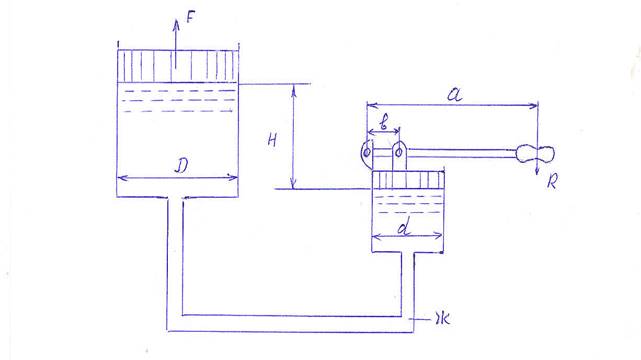
Дано: Ж – вода, g = 9,79 Н/м³; D = 600 мм; d = 150 мм; Н = 1м; а = 700 мм;  R = 100 Н.

Определить силу прессования F.

Решение:

По законам механики к меньшему плунжеру приложено усилие . Это вызывает давление на меньший плунжер

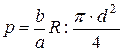
Давление на больший плунжер равно р - gН,  сила прессования будет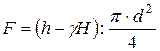

Последовательно получаем:

 

 

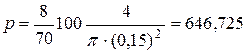
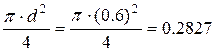
Ответ: F = 180H.

Задача 9.

Поршень диаметром D движется равномерно вниз в цилиндре, подавая жидкость Ж в открытый резервуар с постоянным уровнем. Диаметр трубопровода d, его длина l. когда поршень находится ниже уровня жидкости в резервуаре на Н = 5 м, потребная для его перемещения сила равна F. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять равным l = 0,03. Коэффициент сопротивления выхода в резерв _вых = 1,0.

Дано:

Ж – керосин; g = 7770 – 8450 Н/м³. D = 270 мм, d = 90 мм, = 27 м, Н = 5 м, F = 27 700 Н,  = 0,03, bx = 0,5, вых = 1,0,  = 0,025 см²/с.

Определить:

Скорость поршня и расход жидкости Q.

Решение:

При ламинарном режиме для практических расчетов берут формулу l = 75/Re, значит в нашей задаче Re = 2500.

Скорость керосина в трубопроводе:

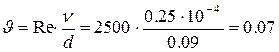 м/с

Площадь сечения трубы 6,36 * 10^-3 м².

Значит расход керосина составляет 0,45 л/с или 4,45*10^-4 м³/с. Площадь сечения насосного цилиндра равна 0,05726 м². отсюда определяется скорость поршня 0,08 м/с или 8 см/с.

Для данного типа трубопровода напорная и пьезометрическая линии выглядят следующим образом.

                                                      

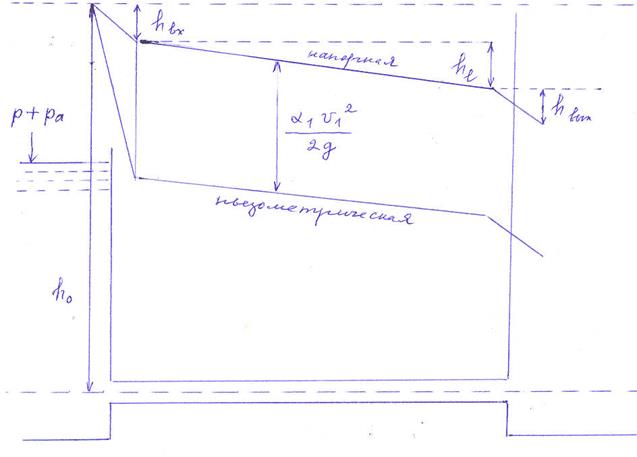
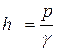
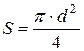    . Получается h = 57 м, h₀ = 52 м.

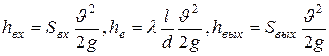
   см,  h_e = 0.2 cм.

И на графике такие  незначительные высоты не видны.

Задача 12.

Дано:  = 0,5 см2/с, d = 100 мм, = 3 м, t = 200 С.

Определить:

Критический напор Н.

Решение:

Формула Пуазейля   Н = 32 2  Rе / (gd3).

Беря в качестве числа Рейнольдса значение 580, получаем Н = 142.

Ответ: Н = 142 м.

Задача 24.

Дано:

δ = 998,2 кг/м3, р0 = 0,75 атм (изб.),  = 112 мм, d = 125 мм, h = 2,5 м,

Q = 25 л/с,  = 6,5, Rе = 0,15 мм.

Определить: Напор Н.

Решение:

Н = h +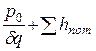

Потери на трение найдём из формулы

Rе = (/ 0,11)4 d

При подстановке конкретных значений суммарные потери оказываются незначительными по сравнению с разностью уровней в баках и пьезометрической высотой.

Ответ: Н = 10 м.

Задача 30.

Дано:

D = 90 мм, S = 260 мм, n = 75 ходов/мин, dn = 72 мм, b = 65 мм, z = 30,

 = 0,9 (поршневой насос),  = 0,86 (шестерённый насос).

Определить:

Частоту вращения n1 шестеренного насоса.

Решение:

Поршневой насос обеспечивает подачу жидкости

 *  D2 S n, шестеренный насос -  * 2

Значит, n1 =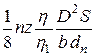

Ответ: n1 = 50 об/мин.

Задача 33.

Дано:

F1 = 9500 Н, F2 = 1350 Н, Q = 14 л/с, D = 20 см, d = 4 см,  = 18,

 = 880 кг/м3,  = .

Определить:

Коэффициент сопротивления .

Решение:

По условию Q1 = Q2 = ½ Q.

Потеря напора h = * .

Суммарный напор в каждой магистрали Н =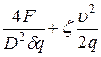

Приравнивая суммарные напоры, получаем

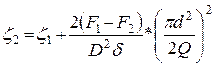
Если подставить конкретные значения, то  = 18 + 9 = 27.