ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО‑ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Филиал в
г. Брянске
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
ЭКОНОМЕТРИКА
|
ВЫПОЛНИЛ(А)
|
Рычкина Е.А.
|
|
СТУДЕНТ(КА)
|
3 курса («вечер», поток 1)
|
|
СПЕЦИАЛЬНОСТЬ
|
Финансы и кредит
|
|
№ ЗАЧ. КНИЖКИ
|
06ФФД11183
|
|
ПРЕПОДАВАТЕЛЬ
|
Шкаберин В.А.
|
Брянск —
2009
Вариант 3
ЗАДАНИЕ
По
предприятиям легкой промышленности региона получена информация, характеризующая
зависимость объема выпускаемой продукции (Y, млн. руб.) от объема капиталовложений (X, млн.
руб.):
|
№ предприятия
|
X
|
Y
|
|
1
|
38
|
69
|
|
2
|
28
|
52
|
|
3
|
27
|
46
|
|
4
|
37
|
63
|
|
5
|
46
|
73
|
|
6
|
27
|
48
|
|
7
|
41
|
67
|
|
8
|
39
|
62
|
|
9
|
28
|
47
|
|
10
|
44
|
67
|
Требуется:
1. Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию углового коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; определить
стандартную ошибку регрессии; построить график остатков.
3. Проверить выполнение предпосылок метода наименьших
квадратов.
4. Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента (уровень значимости a=0,05).
5. Вычислить коэффициент детерминации R2; проверить значимость уравнения регрессии с помощью F-критерия
Фишера (уровень значимости a=0,05); найти среднюю относительную ошибку
аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование значения показателя Y при уровне
значимости a=0,1, если прогнозное значения фактора Х составит 80 % от его максимального
значения.
7. Представить графически: фактические и модельные
значения Y, точки прогноза.
8. Составить уравнения нелинейной регрессии:
·
логарифмической;
·
степенной;
·
показательной.
Привести графики построенных уравнений
регрессии.
9. Для указанных моделей найти коэффициенты детерминации
и средние относительные ошибки аппроксимации.
Сравнить модели по этим характеристикам и сделать вывод.
РЕШЕНИЕ
Для
решения задачи используется табличный процессор EXCEL.
1. С
помощью надстройки «Анализ данных»
проводим регрессионный анализ и определяем параметры уравнения линейной
регрессии 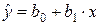 (меню «Сервис»
® «Анализ данных…» ® «Регрессия»):
(меню «Сервис»
® «Анализ данных…» ® «Регрессия»):
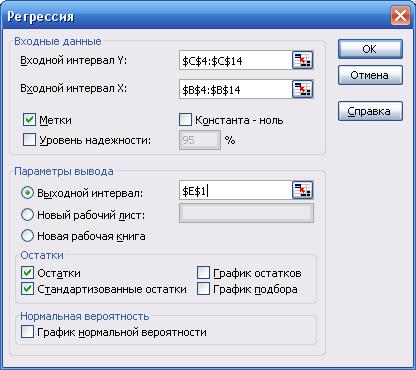
В
результате этого уравнение регрессии будет иметь вид:
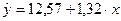 (прил. 1).
(прил. 1).
Угловой
коэффициент b1=1,32 показывает, что при увеличении объема капиталовложений
X на 1 млн. руб. объем выпускаемой продукции Y возрастает в среднем
на 1,32 млн. руб.
2. При проведении регрессионного анализа в EXCEL одновременно были определены остатки регрессии 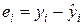 (i=1, 2, …, n,
где n=10 — число наблюдений значений переменных X и Y) (см. «Вывод остатка» в прил. 1) и рассчитана остаточная сумма квадратов
(i=1, 2, …, n,
где n=10 — число наблюдений значений переменных X и Y) (см. «Вывод остатка» в прил. 1) и рассчитана остаточная сумма квадратов
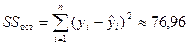 (см. «Дисперсионный анализ» в прил. 1).
(см. «Дисперсионный анализ» в прил. 1).
Стандартная ошибка линейной парной
регрессии Sрег определена
там же:
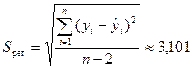 млн. руб.
млн. руб.
(см.
«Регрессионную статистику» в прил. 1).
Стандартная ошибка регрессии Sрег показывает, что
фактические значения объема выпускаемой
продукции Y отличается от расчетных значений в среднем
на 3,101 млн. руб.
График остатков ei от предсказанных уравнением
регрессии значений результата 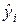 (i=1, 2, …, n) строим с помощью «Мастера диаграмм». Предварительно в «Выводе остатка» в прил. 1
выделяются блоки ячеек «Предсказанное Y» и «Остатки» вместе с заголовками, а затем выбирается пункт меню
«Вставка» ® «Диаграмма…»
® «Точечная»:
(i=1, 2, …, n) строим с помощью «Мастера диаграмм». Предварительно в «Выводе остатка» в прил. 1
выделяются блоки ячеек «Предсказанное Y» и «Остатки» вместе с заголовками, а затем выбирается пункт меню
«Вставка» ® «Диаграмма…»
® «Точечная»:
График
остатков приведен в прил. 2
3. Проверим
выполнение предпосылок обычного метода наименьших квадратов.
1) Случайный характер остатков.
Визуальный анализ графика остатков не
выявляет в них какой-либо явной закономерности.
Проверим
исходные данные на наличие аномальных наблюдений (выбросов) объема
выпускаемой продукции Y. С этой целю сравним абсолютные
величины стандартизированных остатков
(см. «Вывод остатка» в прил. 1)
с табличным значением t-критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы 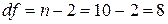 , которое составляет tтаб=2,306 (см. Справочные таблицы).
, которое составляет tтаб=2,306 (см. Справочные таблицы).
Видно,
что ни один из стандартизированных остатков не превышает по абсолютной величине табличное значение t-критерия Стьюдента. Это свидетельствует об отсутствии выбросов.
2) Нулевая средняя величина остатков. Данная
предпосылка всегда выполняется для линейных моделей со свободным коэффициентом b0, параметры которых оцениваются обычным методом
наименьших квадратов. В нашей модели алгебраическая сумма остатков и,
следовательно, их среднее, равны нулю: 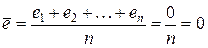 (см. прил. 1).
(см. прил. 1).
Для
вычисления суммы и среднего значений остатков использовались встроенные функции
«СУММ» и «СРЗНАЧ».
3) Одинаковая дисперсия (гомоскедастичность) остатков. Выполнение
данной предпосылки проверим методом Глейзера в предположении линейной
зависимости среднего квадратического отклонения случайной составляющей
регрессионной модели от
значений факторов. Для этого рассчитывается коэффициент корреляции  между абсолютными
величинами остатков
между абсолютными
величинами остатков 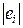 и значениями
и значениями 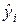 (i=1, 2, …, n) с помощью выражения,
составленного из встроенных функций:
(i=1, 2, …, n) с помощью выражения,
составленного из встроенных функций:
=КОРРЕЛ(ABS(Остатки);Предсказанное_Y)
Коэффициент
корреляции оказался равным 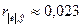 (см. прил. 1).
(см. прил. 1).
Критическое
значение коэффициента корреляции для уровня значимости a=0,05 и числа степеней свободы 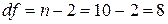 составляет rкр=0,632 (см.
Справочные
таблицы,1).
составляет rкр=0,632 (см.
Справочные
таблицы,1).
Так
как коэффициент корреляции 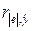 не превышает по абсолютной величине
критическое значение, то
статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на
уровне значимости a=0,05.
не превышает по абсолютной величине
критическое значение, то
статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на
уровне значимости a=0,05.
4) Отсутствие автокорреляции в
остатках. Выполнение данной предпосылки проверяем методом Дарбина–Уотсона.
Предварительно ряд остатков упорядочивается в зависимости от последовательно
возрастающих значений результата Y, предсказанных уравнением регрессии. Для этой цели в
«Выводе остатка» в прил. 1 выделяется любая ячейка в
столбце «Предсказанное Y», и на
панели инструментов нажимается кнопка « » («Сортировка по возрастанию»). По
упорядоченному ряду остатков рассчитываем d‑статистику Дарбина–Уотсона
» («Сортировка по возрастанию»). По
упорядоченному ряду остатков рассчитываем d‑статистику Дарбина–Уотсона
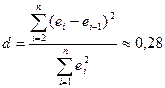 (см. прил. 1).
(см. прил. 1).
Для
расчета d‑статистики
использовалось выражение, составленное
из встроенных функций EXCEL:
=СУММКВРАЗН(«Остатки 2, …, n»; «Остатки
1, …, n–1»)/СУММКВ(«Остатки
1, …,n»)
Критические
значения d‑статистики для числа
наблюдений n=10, числа факторов p=1 и уровня значимости a=0,05 составляют: d1=0,88; d2=1,32 (см. Справочные
таблицы,5).
Так
как выполняется условие
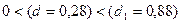 ,
,
статистическая гипотеза об отсутствии
автокорреляции в остатках является положительной на уровне значимости a=0,05.
Примечание:
· если
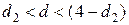 , то остатки признаются независимыми (некоррелированными);
, то остатки признаются независимыми (некоррелированными);
· если
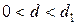 — имеется
положительная автокорреляция;
— имеется
положительная автокорреляция;
· если
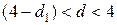 — существует
отрицательная автокорреляция;
— существует
отрицательная автокорреляция;
· если
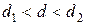 или
или 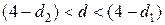 , то это указывает на неопределенность ситуации.
, то это указывает на неопределенность ситуации.
Проверим
отсутствие автокорреляции в остатках также и по коэффициенту автокорреляции
остатков первого порядка
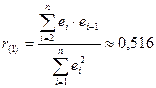 (см. прил. 1).
(см. прил. 1).
(ряд остатков упорядочен в той же самой
последовательности).
Для
расчета коэффициента автокорреляции использовалось выражение, составленное из встроенных функций:
=СУММПРОИЗВ(«Остатки 2, …, n»; «Остатки
1, …, n–1»)/СУММКВ(«Остатки
1, …,n»)
Критическое
значение коэффициента автокорреляции для числа наблюдений n=10 и
уровня значимости a=0,05
составляет r(1)кр=0,632 (см. Справочные таблицы,1). Так
как коэффициент автокорреляции остатков первого порядка не превышает по
абсолютной величине критическое значение, то это еще раз указывает на
отсутствие автокорреляции в остатках.
5) Нормальный закон распределения
остатков. Выполнение этой предпосылки проверяем с помощью R/S-критерия,
определяемого по формуле
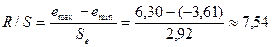 ,
,
где emax=6,30;
emin=(–3,61)
— наибольший и наименьший остатки соответственно (определялись с помощью
встроенных функций «МАКС» и «МИН»; см. прил. 1); 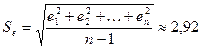 — стандартное
отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН»; см. прил. 1).
— стандартное
отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН»; см. прил. 1).
Критические границы R/S-критерия для числа
наблюдений n=10 и уровня значимости a=0,05 имеют значения: (R/S)1=2,67 и (R/S)2=3,69 (см. Справочные таблицы,2).
Так как расчетное значение R/S-критерия попадает в интервал между критическими границами,
то статистическая гипотеза о нормальном
законе распределения остатков не отклоняется на уровне
значимости a=0,05.
Таким образом, выполняются четыре из пяти предпосылок
обычного метода наименьших квадратов. Это говорит о том, что регрессионная
модель не вполне адекватна исследуемому экономическому явлению, и использовать ее
для целей анализа и прогнозирования индекса
человеческого развития следует с некоторой
осторожностью.
4. Проверим статистическую значимость коэффициентов b0 и b1 уравнения регрессии. Табличное значение t-критерия
Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка линейной парной
регрессии 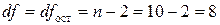 составляет tтаб=2,306 (см. Справочные таблицы,3).
составляет tтаб=2,306 (см. Справочные таблицы,3).
t-статистики
коэффициентов
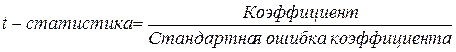 ,
,
были определены при проведении регрессионного анализа
в EXCEL: tb0»2,481; tb1»9,481 (см. прил. 1). Их анализ показывает, что по абсолютной
величине все они превышают табличное значение t-критерия Стьюдента. Это свидетельствует о
статистической значимости обоих коэффициентов.
Статистическая
значимость углового коэффициента b1 дает
основание говорить о существенном (значимом) влиянии изменения объема
капиталовложений X на изменение объема выпускаемой продукции Y.
5. Коэффициент детерминации R2 линейной
модели также был определен при проведении регрессионного анализа:
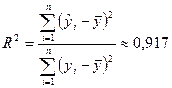
(см. «Регрессионную
статистику» в прил. 1).
Значение R2
показывает, что линейная модель объясняет 91,7 % вариации объема выпускаемой
продукции Y.
F-статистика линейной модели имеет значение
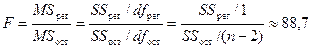
(см. «Дисперсионный
анализ» в прил. 1).
Табличное
значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы 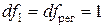 и
и 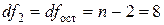 составляет Fтаб=5,32 (см.
Справочные
таблицы, 4). Так как F-статистика превышает табличное значение F-критерия Фишера, то это свидетельствует о
статистической значимости уравнения регрессии в целом.
составляет Fтаб=5,32 (см.
Справочные
таблицы, 4). Так как F-статистика превышает табличное значение F-критерия Фишера, то это свидетельствует о
статистической значимости уравнения регрессии в целом.
Среднюю относительную ошибку аппроксимации определяем по приближенной
формуле
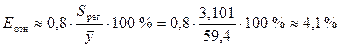 ,
,
где 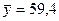 млн. руб. — средний
объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ» (см. «Исходные данные» в прил. 1).
млн. руб. — средний
объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ» (см. «Исходные данные» в прил. 1).
Значение Еотн
показывает, что предсказанные уравнением регрессии значения объема выпускаемой
продукции Y отличаются от фактических значений в среднем на 4,1
%. Линейная модель имеет высокую точность (при 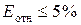 — точность модели
высокая, при
— точность модели
высокая, при 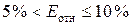 — точность хорошая,
при
— точность хорошая,
при 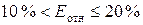 — удовлетворительная,
при
— удовлетворительная,
при 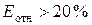 — неудовлетворительная).
— неудовлетворительная).
По
результатам проверок, проведенных в пунктах 3 — 5, можно сделать вывод о высоком
качестве линейной модели и возможности ее использования для целей анализа и
прогнозирования объема выпускаемой продукции.
6. Спрогнозируем объем
выпускаемой продукции Y, если прогнозное значение объема капиталовложений
X составит 80 % от своего максимального значения в исходных
данных:
·
максимальное
значение X — xmax=44 млн.
руб. (см. «Исходные данные» в прил. 1);
·
прогнозное
значение X — 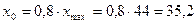 млн. руб.
млн. руб.
Среднее
прогнозируемое значение объема выпускаемой продукции
(точечный
прогноз) равно
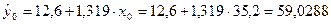 млн. руб.
млн. руб.
Стандартная
ошибка прогноза фактического значения объема выпускаемой продукции y0 рассчитывается по формуле
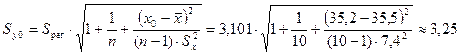 млн. руб.,
млн. руб.,
где 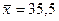 млн. руб. — средний
объем капиталовложений;
млн. руб. — средний
объем капиталовложений; 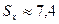 млн. руб. —
стандартное отклонение объема капиталовложений (определены с помощью встроенных
функций «СРЗНАЧ» и «СТАНДОТКЛОН»; см. «Исходные данные» в прил. 1).
млн. руб. —
стандартное отклонение объема капиталовложений (определены с помощью встроенных
функций «СРЗНАЧ» и «СТАНДОТКЛОН»; см. «Исходные данные» в прил. 1).
Интервальный
прогноз фактического значения объема выпускаемой продукции y0 с надежностью (доверительной вероятностью) g=0,9 (уровень значимости
a=0,1) имеет вид:
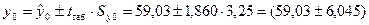 млн. руб.,
млн. руб.,
где
tтаб=1,860 — табличное значение t-критерия Стьюдента при уровне значимости a=0,1
и числе степеней свободы 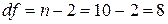 (см. Справочные таблицы,3).
(см. Справочные таблицы,3).
Таким
образом, объем выпускаемой продукции Y с вероятностью 90 %
будет находиться в интервале от 52,985 до 65,075 млн. руб.
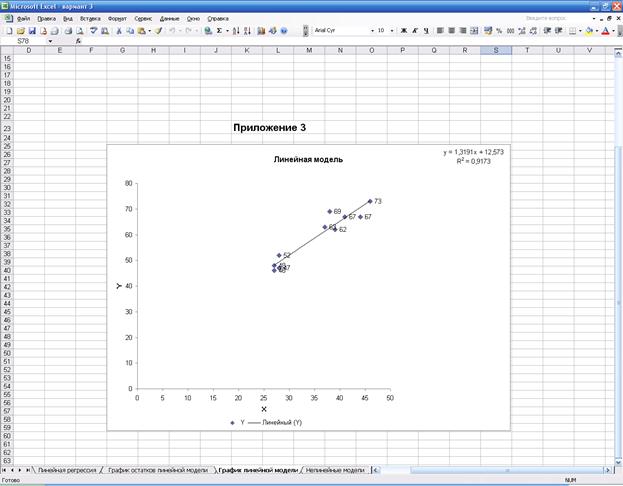
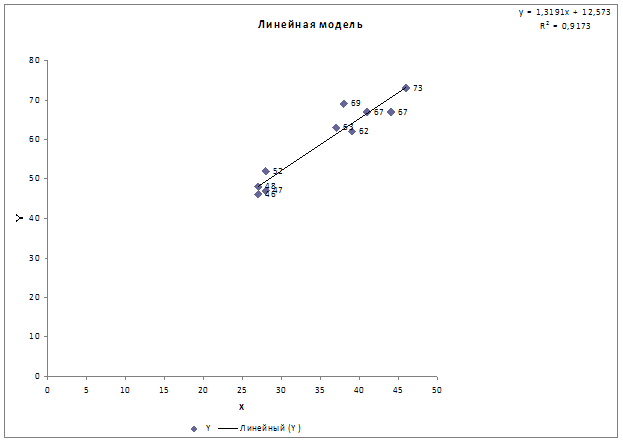
7. График, на котором изображены фактические и
предсказанные уравнением регрессии значения Y строим с помощью «Мастера диаграмм» (меню «Вставка» ® «Диаграмма…»
® «Точечная»). Далее строим линию линейного
тренда (меню «Диаграмма» ® «Добавить
линию тренда…» ® «Линейная»), и устанавливаем
вывод на диаграмме уравнения регрессии и коэффициента детерминации R2:
Точки
точечного и интервального прогнозов наносим на график вручную (прил.
3).
8. Логарифмическую, степенную и показательную модели также строим с
помощью «Мастера диаграмм» (меню «Вставка» ® «Диаграмма…»
® «Точечная»). Далее последовательно строим
соответствующие линии тренда (меню «Диаграмма»
® «Добавить линию тренда…»), и
устанавливаем вывод на диаграмме уравнения регрессии и коэффициента детерминации
R2:
Графики
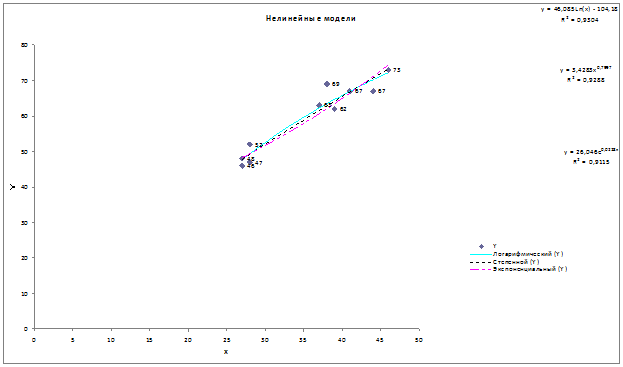
линий регрессии, уравнения регрессии и значения R2 приведены в прил. 4. Рассмотрим последовательно каждую модель.
1) Логарифмическая модель:
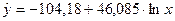 .
.
Значение параметра b1=46,085
показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции
Y возрастает в среднем на 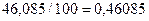 млн. руб.
млн. руб.
Коэффициент
детерминации R2»0,9304 показывает, что логарифмическая модель
объясняет 93,04 % вариации объема выпускаемой продукции Y.
Стандартная ошибка логарифмической
регрессии также рассчитывается через коэффициент детерминации R2:
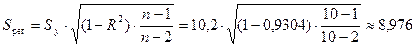 млн. руб.,
млн. руб.,
где 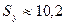 млн. руб. —
стандартное отклонение объема выпускаемой продукции, определенное с помощью
встроенной функции «СТАНДОТКЛОН» (см.
«Исходные данные» в прил. 1).
млн. руб. —
стандартное отклонение объема выпускаемой продукции, определенное с помощью
встроенной функции «СТАНДОТКЛОН» (см.
«Исходные данные» в прил. 1).
Среднюю
относительную ошибку аппроксимации определяем по приближенной формуле
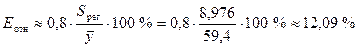 .
.
Предсказанные
уравнением логарифмической регрессии значения объема выпускаемой продукции Y отличаются
от фактических значений в среднем на 8,976 млн. руб. или на 12,09 %.
Логарифмическая модель имеет хорошую точность.
2)
Степенная модель:
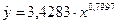 .
.
Показатель степени b1=0,7997
показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции
Y возрастает в среднем на 0,7997 %.
Коэффициент
детерминации R2»0,9288 показывает, что степенная модель объясняет 92,88
% вариации объема выпускаемой продукции Y.
Стандартная ошибка степенной регрессии
равна
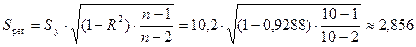 млн. руб.
млн. руб.
Средняя
относительная ошибка аппроксимации имеет значение
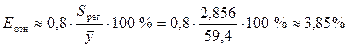 .
.
Предсказанные
уравнением степенной регрессии значения объема выпускаемой продукции Y отличаются
от фактических значений в среднем на 2,856 млн. руб. или на 3,85 %. Степенная
модель имеет хорошую точность.
3)
Показательная (экспоненциальная) модель:
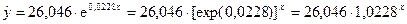 ,
,
где
е=2,718… — основание натуральных логарифмов; 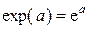 — функция экспоненты
(в EXCEL встроенная функция
«EXP»).
— функция экспоненты
(в EXCEL встроенная функция
«EXP»).
Параметр b1=1,0228 показывает, что при увеличении объема
капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y возрастает в
среднем в 1,0228 раза, то есть на 2,28 %.
Коэффициент
детерминации R2»0,9115 показывает, что показательная модель объясняет 91,15
% вариации объема выпускаемой продукции Y.
Стандартная ошибка показательной
регрессии:
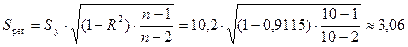 млн. руб.
млн. руб.
Средняя
относительная ошибка аппроксимации:
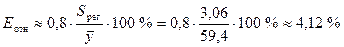 .
.
Предсказанные
уравнением показательной регрессии значения объема выпускаемой продукции Y отличаются
от фактических значений в среднем на 3,06 млн. руб. или на 4,12 %.
Показательная модель имеет хорошую точность.
Сравнивая
между собой коэффициенты детерминации R2
четырех построенных моделей (линейной, логарифмической, степенной и
показательной), можно придти к выводу, что лучшей моделью является
логарифмическая модель, так как она имеет самое большое значение R2.
ПРИЛОЖЕНИЕ 1

ПРИЛОЖЕНИЕ 2
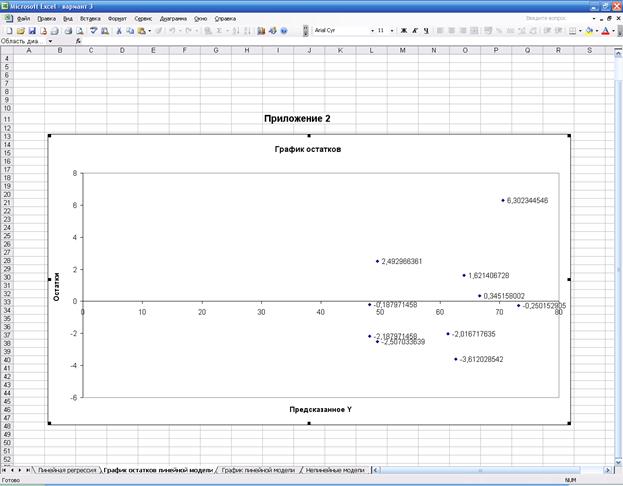
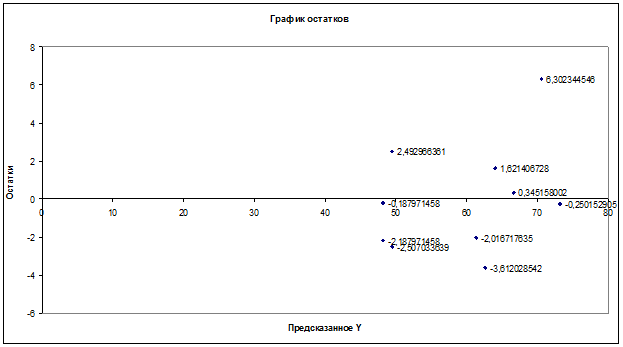
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 4