Задача 7

Привести систему к системе с базисом, найти соответствующее базисное решение и сделать проверку, подставив решение в исходную систему.

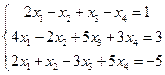
Решение.

Приводим систему к системе с базисом, работая с матрицей системы:

2	-1	3	-4	1
4	-2	5	3	3
2	1	-3	5	-5

2	-1	3	-4	1
0	0	-1	11	1
0	2	-6	9	-6

2	-1	3	-4	1
0	2	-6	9	-6
0	0	1	-11	-1

2	-1	0	29	4
0	2	0	-57	-12
0	0	1	-11	-1

2	0	0	0,5	-2
0	1	0	-28,5	-6
0	0	1	-11	-1

1	0	0	0,25	-1
0	1	0	-28,5	-6
0	0	1	-11	-1

Получаем систему с базисом:

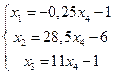
Соответствующее базисное решение: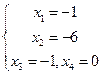

Сделаем проверку, подставив решение в исходную систему.

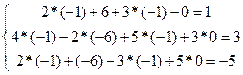
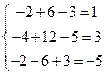верно.

Задача 27

Предположим, что для производства двух видов продукции А и В можно использовать только материал трех сортов. При этом на изготовление единицы изделия вида А расходуется 2 кг материала первого сорта, 4 кг материала второго сорта и 4 кг материала третьего сорта. На изготовление единицы изделия вида В расходуется 3 кг материала первого сорта, 2 кг материала второго сорта и 5 кг материала третьего сорта. На складе фабрики имеется всего материала первого сорта 35 кг, второго сорта - 38 кг, третьего сорта – 59 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 8 тыс. руб., а от единицы готовой продукции вида В прибыль составляет 7 тыс. руб.

Определить максимальную прибыль от реализации всей продукции видов А и В. Решить задачу симплексным методом и графически.

Решение.

Математическая модель оптимизации выпуска продукции может быть записана в следующем виде:

Найти неизвестные значения переменных х₁ и х₂, удовлетворяющие ограничениям

2х₁ +3х₂£ 35

4х₁ + 2х₂£ 38

4х₁ + 5х₂£ 59

х₁ ³0, х₂³0

и доставляющих максимальное значение целевой функции Z = 8х₁ + 7х₂® max.

Решим задачу симплексным методом.

Вводим неотрицательные балансовые переменные:

у ₁= - 2х₁ -3х₂ +35

у ₂= -4х₁ - 2х₂+ 38

у ₃= -4х₁ - 5х₂+ 59

Составляем симплексную таблицу:

Таблица №1	- х₁	-х₂	1
у ₁=	2	3	35
у ₂=	4	2	38
у ₃=	4	5	59
Z =	-8	-7	0

Начальное решение: х₁=0, х₂= 0. При этом значение целевой функции Z =0.

Так как последняя строка содержит отрицательные элементы, полученное решение не оптимально.

Пусть 1-й столбец является разрешающим. min{ 35/2, 38/4, 59/4} = 38/4, следовательно, вторая строка разрешающая.

Таблица №2	- у ₂	-х₂	1
у ₁=	-1/2	2	16
х₁=	1/4	1/2	19/2
у ₃=	-1	3	21
Z =	2	-3	76

Решение: х₁=19/2, х₂= 0. При этом значение целевой функции Z =76.

Так как последняя строка содержит отрицательные элементы, полученное решение не оптимально.

Пусть 2-й столбец является разрешающим. min{16/2, 19/1, 21/3} = 21/3, следовательно, третья строка разрешающая.

Таблица №3	- у ₂	- у ₃	1
у ₁=			2
х₁=			6
х₂=			7
Z =	1	1	97

Так как последняя строка не содержит отрицательных элементов, полученное решение оптимально.

Решение: х₁* = 6, х₂*= 7 . При этом значение целевой функции Z* =97..

Решим задачу графически. Построим множество допустимых решений или область допустимых решений. Проводим перпендикулярные оси координат: горизонтальная – ось Ох₁, вертикальная - Ох₂. Условия неотрицательности переменных х₁ ³0, х₂³0 показывают, что область допустимых решений будет лежать в первом квадранте системы координат. Для изображения на плоскости множества точек, координаты которых удовлетворяют оставшимся ограничениям модели, рассмотрим уравнения, получаемые из неравенств модели заменой знака «£» на знак «=». В результате такой замены получим три линейных уравнения прямых:

2х₁ +3х₂= 35	(1)
4х₁ + 2х₂= 38	(2)
4х₁ + 5х₂=59	(3)

Прямая (1) проходит через точки с координатами (0;11,7) и (17,5;0).

Прямая (2) проходит через точки с координатами (0;19) и (9,5;0).

Прямая (3) проходит через точки с координатами (0;11,8) и (14,75;0).

Каждая прямая делит плоскость на две полуплоскости. Точки расположенные по одну сторону прямой, удовлетворяют соответствующему неравенству, а точки, расположенные по другую сторону, не удовлетворяют. Для того, чтобы определить искомую полуплоскость, выбирается некоторая «тестовая» точка и ее координаты подставляются в левую часть неравенства. Если для этой точки неравенство выполняется, то она лежит в искомой полуплоскости, т.е. все точки этой полуплоскости удовлетворяют неравенству модели. Если же для «тестовой» точки неравенство не выполняется, то искомой будет та полуплоскость, которая не содержит эту точку. Взяв в качестве «тестовой» точку с координатами (0;0), убеждаемся, что она удовлетворяет всем неравенствам модели.

Следовательно, все полуплоскости, соответствующие неравенствам модели, содержат точку (0,0).

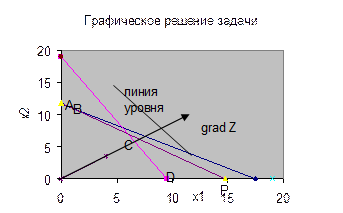
Множество допустимых решений является пересечением всех допустимых полуплоскостей и представляет собой многоугольник АВСDО.

Для нахождения оптимального решения задачи необходимо определить направление возрастания целевой функции.

Вектор, компоненты которого являются коэффициентами целевой функции при переменных х₁ и х₂, называют вектором – градиентом целевой функции и обозначают grad Z.

Целевая функция может возрастать до тех пор, пока линии уровня соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и линии уровня, соответствующей максимально возможному значению целевой функции, и будет точкой максимума.

На рисунке видно, что оптимальное решение соответствует точке В, лежащей на пересечении прямых (2) и (3). Поэтому ее координаты находим как решение системы линейных уравнений, задающих эти прямые:

4х₁ + 2х₂= 38

4х₁ + 5х₂=59

Решая эту систему, находим х₁* = 6, х₂*= 7 . При этом значение целевой функции Z = 8*х₁* + 7*х₂* = 8 ´ 6+ 7´ 7 =97.

Полученное решение означает, что предприятию необходимо ежемесячно производить 6 единиц продукции А и 7 единиц продукции Б, что позволит ему получать максимальную прибыль в размере 97 тысяч рублей.

Задача 47

Для модели предыдущей задачи составить двойственную, из симплексной таблицы найти ее решение и проверить по основной теореме.

Решение

Построение двойственной задачи.

Найти неизвестные значения переменных u_1, u₂, u₃ , удовлетворяющих ограничениям:

2u₁ + 4u₂ + 4u₃ ³ 8

3u₁ + 2u₂ + 5u₃ ³ 7

u₁ ³0, u₂ ³0, u₃ ³ 0

и доставляющих минимальное значение целевой функции

W = 35u₁ + 38u₂ + 59u₃® min.

Элементы последней строки заключительной симплексной таблицы равно оптимальным значениям переменных двойственной задачи:

u₁* = 0, u₂* = 1, u₃* = 1

Вычислим оптимальное значение целевой функции двойственной задачи:

W = 35 × 0 + 38 ×1 + 59 × 1 = 97, т.е. Z* = W*, что соответствует первой теореме двойственности.

Задача 67

Решить транспортную задачу.

7

5

3

2

1

С =

3

4

8

4

5

2

2

5

6

9

1

3

6

5

8

А=(100, 120, 80, 200), В=(100, 150,100, 75, 75).

Решение:

Находим 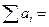100+120+80+200=500,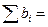100+150+100+75+75=500.

Задача с правильным балансом (закрытая). Находим начальное опорное решение 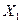методом минимальной стоимости.

Потенциал

v

1

3

6

2

1

u

                      b

а

100

150

100

75

75

7

5

3

2

1

0

100

+

25

-

75

3

4

8

4

5

2

120

70

-

50

+

2

2

5

6

9

-1

80

80

1

3

6

5

8

0

200

100

70

30

.

Находим потенциалы строк 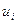и столбцов 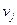, используя соотношения 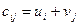для занятых клеток и полагая . Для свободных клеток находим знаки выражений 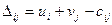. Так как 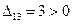решение 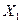не является оптимальным. По циклу, содержащему клетку (1,3), перемещаем поставку 25.

Потенциал

v

-2

0

3

-1

1

u

       b

а

100

150

100

75

75

7

5

3

2

1

0

100

25

75

3

4

8

4

5

5

120

45

75

2

2

5

6

9

2

80

80

1

3

6

5

8

3

200

100

70

30

Так как 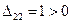решение 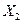не является оптимальным. По циклу, содержащему клетку (1,3), перемещаем поставку 45.

Потенциал

v

-2

0

3

0

1

u

         b

а

100

150

100

75

75

7

5

3

2

1

0

100

25

75

3

4

8

4

5

4

120

45

75

2

2

5

6

9

2

80

80

1

3

6

5

8

3

200

100

25

75

Так как для всех свободных ячеек 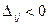полученное решение

0

0

25

0

75

Х =

0

45

0

75

0

0

80

0

0

0

100

25

75

0

0

является оптимальным. Минимальная стоимость перевозок:

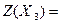25*3+75*1+45*4+75*4+80*2+100*1+25*3+75*6=1415.

Потенциал	v	1		3		6		2		1
u	b а	100		150		100		75		75
			7		5		3		2		1
0	100						+	25	-	75
			3		4		8		4		5
2	120					70	-	50	+
			2		2		5		6		9
-1	80			80
			1		3		6		5		8
0	200	100		70		30