Написать программу, которая
демонстрирует некоммутативность операций:
масштабирования и вращения.
Некоммутативность
– это зависимость произведения от порядка сомножителей, то есть a*b ¹ b*a. В данном задании некоммутативность операций масштабирования и вращения также
означает, что результат может получиться разным, в зависимости от того, какая
операция будет произведена первой.
Вспомним, что как реализуются преобразования точки и
фигуры в 2хмерном пространстве:
Преобразование точки
Точка на плоскости представляется
двумя координатами: |x y|.
Матрица преобразования точки выглядит так:

Ниже показано
преобразование точки через квадратную матрицу; здесь xn
= xa + yc и yn = xb + yd — новые координаты точки после преобразования:
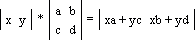
Преобразование фигуры
Если представить
фигуру как совокупность точек, то можно провести и ее преобразование. В
следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1),
каждая из которых после преобразования переходит соответственно в A*(0,
0), B*(a, b), C*(a + c, b
+ d), D*(c, d):
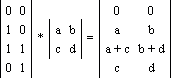
(Мишенин О.И., Компьютерная графика, уч.
пособие, 2004)
В случае масштабирования
a = kx - коэффициент масштабирования по оси x
d = ky - коэффициент
масштабирования по оси y
b = c = 0
А в случае поворота на угол a
a = d =
cos(a)
b = sin(a)
c = - sin(a)
Таким образом, для получения
новых координат точки нужно умножить вектор, представляющий эту точку, на
матрицу преобразования. Так как операции матричного умножения некоммутативны, то из этого следует что и преобразования некоммутативны. В частном случае они могут быть
коммутативны, например если при масштабировании коэффициенты по осям x и y равны между собой.
Программа демонстрирует это: над
фигурой, состоящей из точек, производятся операции масштабирования и поворота.
При этом видно, что конечный результат зависит от того, какая операция была
произведена первой.
Написать программу построения плоской кривой, содержащей
узлы. Использовать В-сплайны
Полученная гладкая кривая называется кубическим
сплайном. Термин «сплайн» возник по аналогии: это название чертежного
инструмента — тонкой металлической линейки, которая может изгибаться так, чтобы
проходить через заданные точки. Физически такая кривая минимизирует энергию
внутренних напряжений. Математически — имеет минимальную среднеквадратичную
кривизну, то есть она наиболее гладкая. Сплайны имеют много приложений в
конструировании криволинейных форм.
Сплайн может не проходить через
узлы, но при этом проходит наиболее близко к ним.
Программа демонстрирует ломаную
линию и сплайн, который гладко следует изгибам линии. Видно, что сплайн не
достает до начальной и конечной точек – его задача не в этом, а в том, чтобы
гладко отработать изгибы.
Написать программу для
изображения многоугольника, вращающегося в пространстве
Программа хранит координаты фигуры (точнее, её вершин,
объединенных в грани) в трехмерном пространстве. Эти координаты привязаны к
системе координат, которая называется система координат фигуры. Для отображения
вращения координаты пересчитываются в глобальную систему координат. В ней уже
содержатся координаты фигуры, которая была повернута на определенный угол. При
этом по направлению нормали к плоскости грани определяется, видна эта грань
(нормаль направлена на зрителя) или не видна, чтобы отрисовывать
её сплошной или пунктирной линией. После этого трехмерные глобальные координаты
пересчитываются в экранные, используя проекцию «перспектива с 2мя точками
схода», которые используются для отображения на экране.
Несколько раз в секунду значение угла поворота изменяется,
заново пересчитываются глобальные координаты, определяется видимость граней, пересчитываеются и используются для отображения двухмерные
координаты на экране.