ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

О Т Ч Е Т

о результатах выполнения лабораторной работы по дисциплине

«Экономико-математические методы и прикладные модели»

Вариант № 92

Выполнила: ст. 3 курса,

финансово-кредитный факультет,

№ зачетной книжки

Проверил:

Пенза - 2008

ЗАДАЧА 1.

1. ПОСТАНОВКА ЗАДАЧИ 5:

Необходимо решить транспортную задачу – минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объем заказа и количество продукции, хранящейся на каждом складе.

Таблица тарифов на перевозку продукции и объемов запасов на складе и заказов:

Таблица 1.

2. РАЗРАБОТКА ЭММ:

В данной задаче предложение превышает спрос, предложение составляет 151 единицу, а спрос – 105 единиц, поэтому введём фиктивный магазин,  заказ которого будет составлять  46 единиц продукции и добавим его в таблицу. Тогда она будет выглядеть след. образом (см. рис. 14)

х_ij – количество единиц груза (продукции), запланированных к перевозке от склада в заказчику. Стоимость перевозки от i-ого склада к j-ому заказчику составит с_ij х_ij.

F(х) = 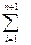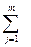c_ijx_ij → min – стоимость перевозок от всех складов ко всем заказчикам, т.е. целевая функция.

Ограничения в данной задаче будут складываться из условий:

Вся продукция была вывезена со складов 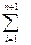x_ij = a_i  i = 1,…, n

Спрос всех заказчиков был удовлетворён 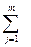 x_ij = b_j j = 1,…, m+1

Количество единиц продукции не может быть отрицательным числом   х_ij ≥ 0.

Распишем целевую функцию:

F(X) = х₁₁*5 + х₁₂*3 + х₁₃ *7 + х₁₄*2 + х₁₅*0 + х₂₁*2 + х₂₂*6   +

+ х₂₃*4 + х₂₄*5 + х₂₅*0 + х₃₁*3 + х₃₂*7 + х₃₃*1 + х₃₄*9 + х₃₅*0 +

+ х₄₁*6 + х₄₂*4 + х₄₃*8 + х₄₄*3 + х₄₅*0 → min

Ограничения:

По строкам:

5х₁₁+3х₁₂+7х₁₃+2х₁₄+ 0х₁₅  = 25

2х₂₁+6х₂₂+4х₂₃+5х₂₄+ 0х₂₅  = 36

3х₃₁+7х₃₂+1х₃₃+9х₃₄+ 0х₃₅  = 40

6х₄₁+4х₄₂+8х₄₃+3х₄₄+ 0х₄₅  = 50

По столбцам:

5х₁₁ + 2х₂₁ + 3х₃₁ + 6х₄₁ = 20

3х₁₂ + 6х₂₂ + 7х₃₂ + 4х₄₂ = 45

7х₁₃ + 4х₂₃ + 1х₃₃ + 8х₄₃ = 15

2х₁₄ + 5х₂₄ + 9х₃₄ + 3х₄₄  = 25

0х₁₅ + 0х₂₅ + 0х₃₅ + 0х₄₅ = 46

3. ОПИСАНИЕ ИНФОРМАЦИОННОЙ ТЕХНОЛОГИИ ПОЛУЧЕНИЯ ОПТИМАЛЬНОГО РЕШЕНИЯ:

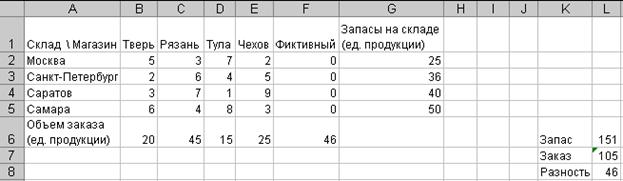
Рис. 1. Исходные данные.

Создадим матрицу перевозок (в ячейках B9:F12).

Определим целевую функцию. После этого лист MS Excel будет выглядеть следующим образом.

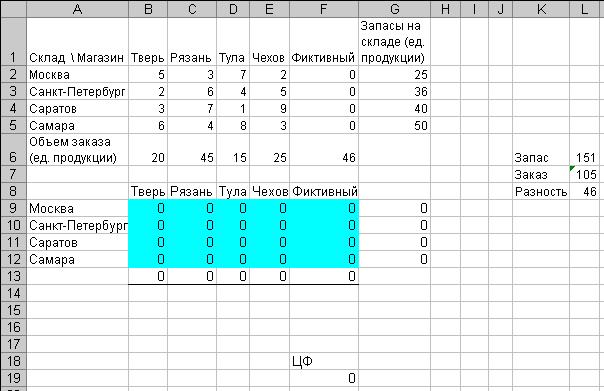
Рис. 2. Матрица перевозок

Целевая функция расположена в ячейке F19 и будет определяться как сумма произведений элементов первой матрицы на соответствующие элементы второй матрицы.

Тот же лист можно представить  в виде формул (Рис.3). Для этого в меню Сервис выбираем Параметры и в закладке «Вид» ставим галочку в окошке Формулы.

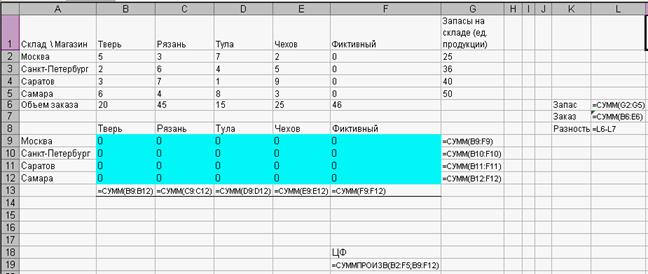
Рис. 3. Исходный лист в формульном режиме

Далее, для решения задачи запускаем команду Поиск решения в меню Сервис. Необходимо установить целевую ячейку ($F$19), изменяемые ячейки ($B$9:$F$12). Для этого поместим курсор в требуемые ячейки и введем нужные адреса ячеек. Вводим тип целевой функции: по условию задачи, она равна минимальному значению. Поместим указатель мыши на кнопку «Добавить» и введем ограничения. Завершив ввод необходимых данных, диалоговое окно примет вид:

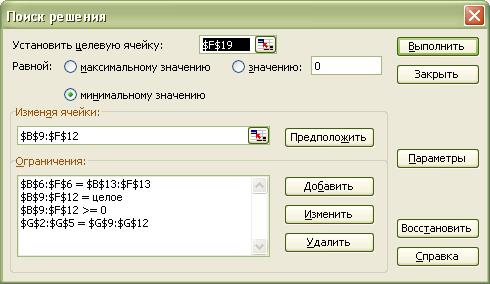
Рис. 4. Поиск решения

Нажимаем кнопку «Выполнить». Через непродолжительное время появляется диалоговое окно «Результаты поиска решения», где указываем тип отчета: по результатам.

Рис. 5. Результаты поиска решения

Нажимаем «ОК». После этого в исходной таблице появляются заполненные ячейки искомых данных $B$9:$F$12 для значений Х_ij и ячейка $F$19 c минимальным значением целевой функции (Рис.6).

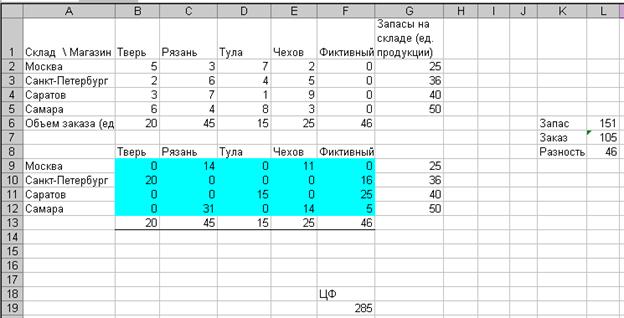
Рис. 6. Готовое решение задачи.

Вот при таком оптимальном плане поставок все ресурсы будут исчерпаны, вся продукция доставлена заказчикам.

Отчет по результатам будет выглядеть следующим образом (Рис.7).

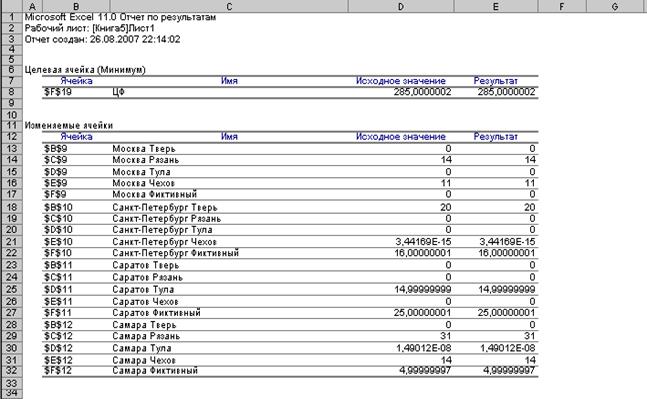
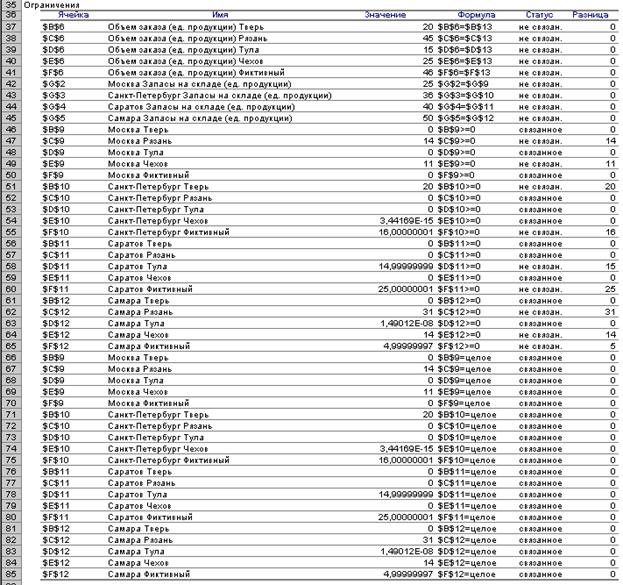
Рис.7. Отчет по результатам

4. РЕКОМЕНДАЦИИ ЛИЦУ, ОТВЕТСТВЕННОМУ ЗА ПРИНЯТИЕ РЕШЕНИЙ:

В ходе решения данной транспортной задачи был получен оптимальный план поставок продукции, при котором минимальные расходы на доставку продукции заказчикам со складов фирмы равны 285 ден.ед., все потребности заказчиков удовлетворены и все грузы вывезены со складов.

ЗАДАЧА 2.

1. ПОСТАНОВКА ЗАДАЧИ 17:

Хлебозавод имеет возможность производить различные хле­бобулочные изделия. Нормы затрат различных типов сырья, их наличие и стоимость единицы продукции каждого вид» приведе­ны ниже (таблица 2).

После проведения маркетинговых исследований установле­но, что ежедневный спрос на «Бородинский» хлеб колеблется в пределах от 150 до 300 кг; спрос на хлеб «Жито» меняется соот­ветственно от 300 до 450 кг; на батон «Чайный» — от 200 до 300 кг; на батон «Городской» — от 200 до 400 кг. Определить оптимальный ежедневный объем выпускаемой хлебобулочной продукции, обес­печивающий максимальную ее стоимость.

Таблица 2.

2. РАЗРАБОТКА ЭММ:

Пусть  х₁, х_2, х₃ и х₄   - количество типов хлебобулочных изделий.

Целевая функция -  стоимость продукции, которую необходимо максимизировать:

F(х) = 7х₁+ 8х₂+ 9 х₃  +  8 х₄                    max .

Ограничения по наличию:

0,2х1+0,15х2+0,4х3+0,35х4 ≤ 500 (кг) -  по наличию муки пшеничной

0,25х1+0,3х2 ≤ 250 (кг) - по наличию муки ржаной

0,02х1+0,025х2+0,04х3+0,035х4 ≤  100 (кг) -   по наличию яиц

0,005х1+0,005х2+0,01х3+0,01х4 ≤  15 (кг) -   по наличию дрожжей

Ограничения по спросу:

150≤0,65х1≤300 (кг) на хлеб «Бородинский»

300≤0,85х2≤450 (кг) на хлеб «Жито»

200≤0,7х3≤300 (кг) на батон «Чайный»

200≤0,6х4≤400 (кг) на батон «Городской»

       Также, на переменные накладываются условия неотрицательности и целочисленности:

х_i ≥ 0,  х_i – целое.

3. ОПИСАНИЕ ИНФОРМАЦИОННОЙ ТЕХНОЛОГИИ ПОЛУЧЕНИЯ ОПТИМАЛЬНОГО РЕШЕНИЯ:

Задача сводится к нахождению неотрицательных переменных х_1,  х_2, х_3,  удовлетворяющих нелинейным ограничениям и доставляющих максимум нелинейной целевой функции.

 Рабочий лист Excel  может быть подготовлен в виде (см. рис.8).           

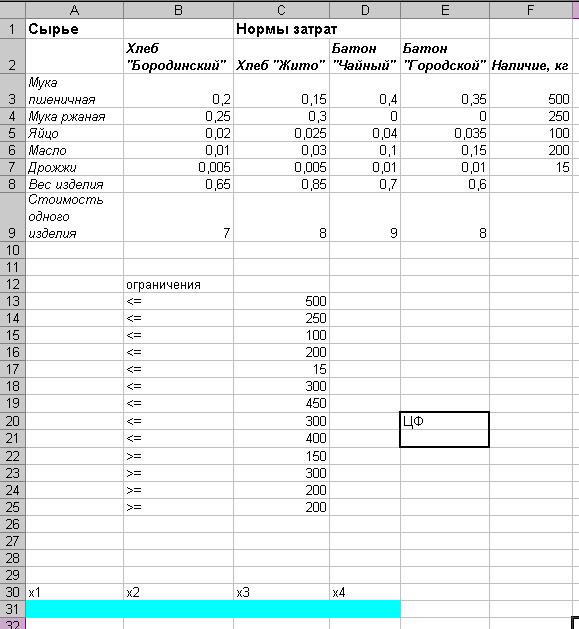
Рис.8. Исходные данные

В ячейках А13: А17 будут суммы по строкам. В ячейки А18:А25 введем формулы.

 В ячейку Е21 введём формулу для вычисления целевой функции (все формулы, ведённые в вышеперечисленные ячейки отражены на рис. 10).

Для того чтобы на листе MS Excel отобразились формулы, заходим в меню «Сервис». В открывшимся диалоговом окне выбираем  «Параметры», откроется окно. В этом окне вкладку «Вид» и ставим галочку перед «Формулы». Данная операция представлена на рисунке 9.

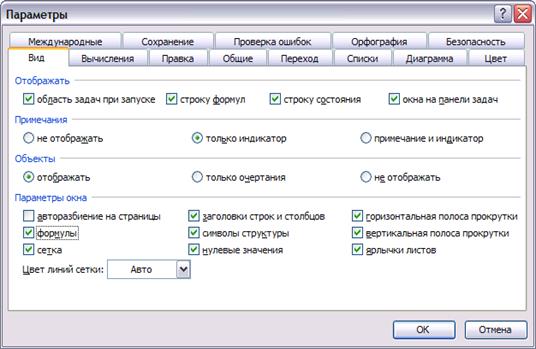
Рис. 9.  Меню Сервис, «Параметры».

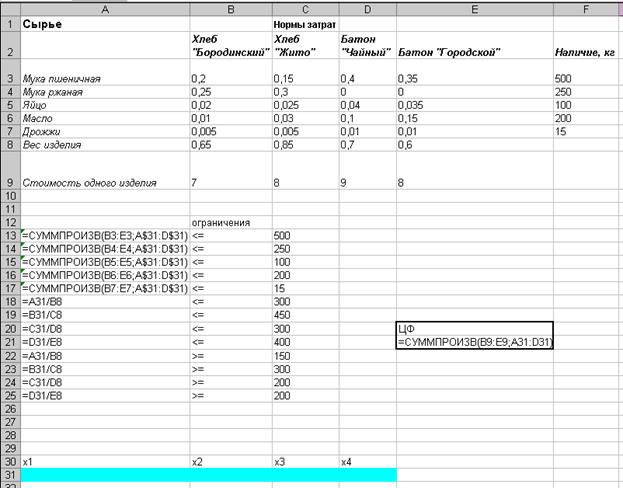
Рис. 10. Исходный лист MS Excel с формулами

Выбираем меню «Сервис». В открывшимся диалоговом окне выбираем  «Поиск решения», в появившимся окне вводим ячейку, в которую будет помещено значение целевой функции (Е21), указываем, что оно должно быть максимальным, из условия задачи. Введем ограничения, для этого выбираем «добавить» и в появившемся диалоговом окне «Добавление ограничения» вводим ограничения. Данная операция показана на рис. 11.

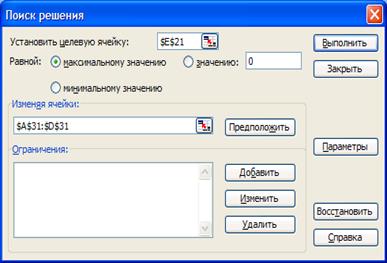
Рис.11. Поиск решения

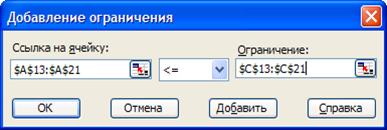
Рис. 12. Ограничения по наличию.

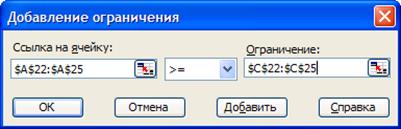
Рис.13. Добавление ограничения

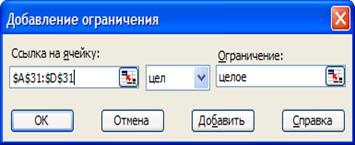
Рис. 14. Ограничение о целочисленности значений переменных

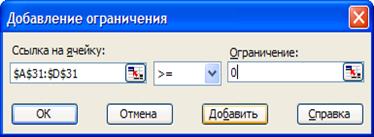
Рис. 15. Ограничение о неотрицательности значений переменных

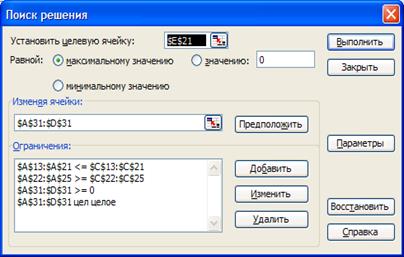
Рис.16. Поиск решения

.

В окне «Поиск решения» нажимаем на кнопку «Параметры» и ставим галочку перед «Неотрицательные значения» «Линейная модель»,  как показано на рис. 16

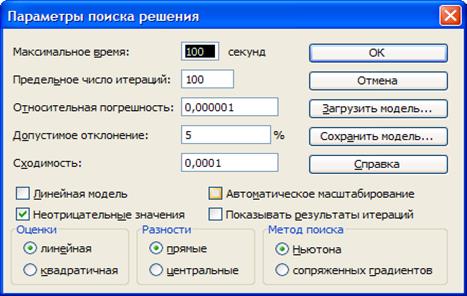
Рис.16. Параметры поиска решения

Нажимаем на кнопку ОК, перед нами снова появилось окно «Поиск решения». Нажимаем кнопку «Выполнить», появляется диалоговое окно «Результаты поиска решения». Для того чтобы у нас на листе MS Excel получился «Отчёт по результатам», выбираем его тип, для этого щёлкаем на него левой кнопкой мышки, и нажимаем «ОК» (см. рис. 17).

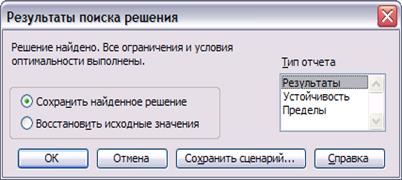
Рис.17. Результаты поиска решения

В итоге в MS Excel появилось окно с готовым решением – рис. 18.

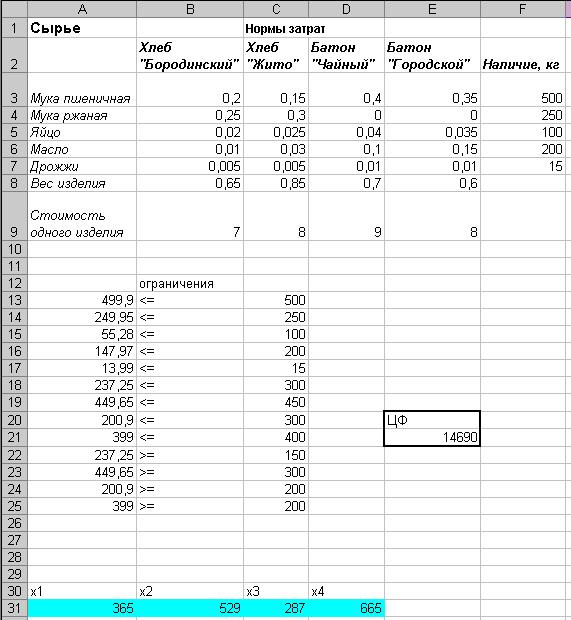
Рис. 18. Готовое решение задачи.

В результате решения был получении ответ, для того чтобы получить максимальную прибыль –14690 денежных единиц необходимо выпускать: Хлеб

«Бородинский» - 365 ед., Хлеб «Жито» - 529 ед., Батон «Чайный» - 287 ед., Батон «Городской» - 665 ед.

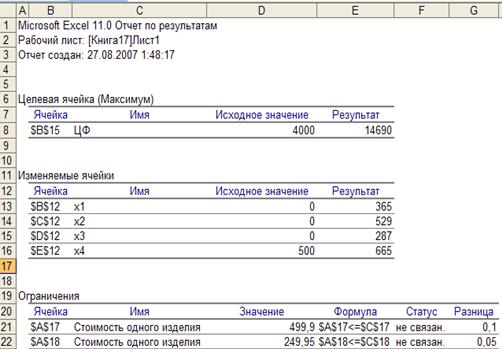
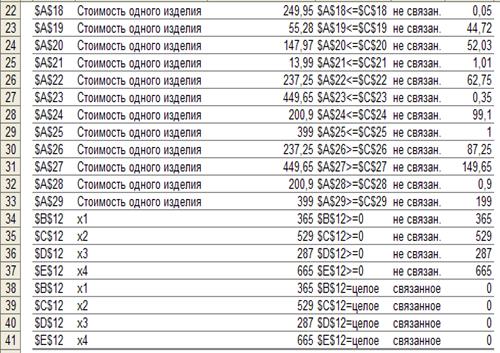
Рис. 19. Отчёт по результатам.

В отчёте по результатам  (рис. 19) содержатся оптимальные значения переменных, равные 365, 529, 287 и 665 ед. (сколько каждого вида продукции нужно производить).

Значение целевой функции равно 14690  денежных единиц – это максимальная прибыль.

Левые части ограничений означают, сколько требуется каждого ресурса для изготовления продукции. Статус «не связан» означает, что ресурс не является дефицитным.

Отчёты по пределам и устойчивости неприменимы для задач с целочисленным условием.