Задача
№ 3
Необходимо
решить транспортную задачу: минимизировать расходы на доставку продукции
заказчикам со складов фирмы, учитывая следующие затраты на доставку одной
единицы продукции, объём заказа и количество продукции, хранящейся на каждом
складе:
Таблица тарифов на перевозку продукции и объёмов запасов на складе и
заказов :
|
 Магазин
Склад
|
ВДНХ
|
Юго—Запад-ная
|
Фили
|
Арбат-ская
|
Соколь-ники
|
Запасы на складе
(ед.прод)
|
|
Пролетарская
|
10
|
8
|
3
|
15
|
16
|
60
|
|
Митино
|
7
|
5
|
9
|
4
|
6
|
30
|
|
Строгино
|
2
|
0
|
14
|
5
|
20
|
40
|
|
Объём заказа (ед.прод)
|
10
|
20
|
40
|
30
|
65
|
|
Решение
Экономико-математическая
модель.
f = 10х11 + 8х12 + 3х13 + 15х14 +
16х15 + 7х21 + 5х22 + 9х23 + 4х24 + 6х25 + 2х31 + 0х32 + 14х33 + 5х34 + 20х35 →
min
х11
+х12 + х13 + х14 + х15 = 60
х21
+ х22 + х23 + х24 +х25 = 30
х31
+ х32 + х33+ х34 + х35 = 40
х11
+ х21 + х31 = 10
х12
+ х22 + х32 = 20
х13
+ х23 + х33 = 40
х14
+ х24 + х34 = 65
Хij ≥ 0, целое
1) Вводим
исходные данные
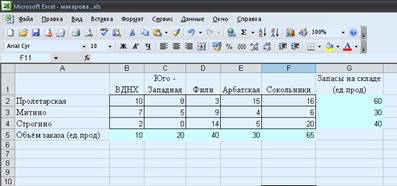
2) Создаем
матрицу перевозок
3)
Введем ограничения по запасам на складе:
х11 + х12 + х13
+ х14 + х15 = 60;
х21 + х22 + х23
+ х24 + х25 = 30;
х31 + х32 + х33
+ х34 + х35 = 40.
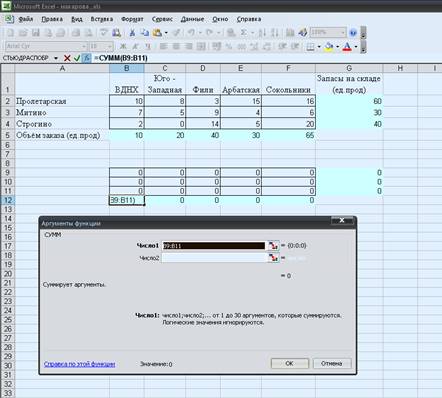
В ячейку G9 вводим формулу: «вставка» →
«функция» → СУММПРОИЗВ → в массив1 вводим
(В9-F9).
Протягиваем функцию на ячейки G10 и G11.
Введем ограничения по объемам заказа:
х11 + х21 + х31 = 10
х12 + х22 + х32 = 20
х13 + х23 + х33 = 40
х14 + х24 + х34 = 65
В ячейку В12 вводим формулу:
«вставка» → «функция» → СУММПРОИЗВ →
в массив1 вводим (В9-В11).
Протягиваем функцию на ячейки С12, D12, E12 и F12.
4)
Стремимся к минимальному значению, т.к. мы минимизируем совокупные транспортные
издержки,
f = 10х11 + 8х12 + 3х13 + 15х14 +
16х15 + 7х21 + 5х22 + 9х23 + 4х24 + 6х25 + 2х31 + 0х32 + 14х33 + 5х34 + 20х35 →
min
В задаче
целевая функция равна сумме произведений удельных транспортных расходов (В9-F11) и количества перевозок (В2-F4), для этого:
В ячейку
В15 вводим функцию:
«вставка» → «функция» → СУММПРОИЗВ → в массив1 вводим (В2-F4), в массив2 вводим (В9-F11).
5) Вводим данные в меню команды «Поиск решения»
$B$15 – целевая
ячейка,
Изменяя
ячейки ($B$9:$F$11)
Ограничения:
$B$9:$F$11 = целое
$B$12:$F$12 ≤ $B$5:$F$5
$G$9:$G$11 = $G$2:$G$4
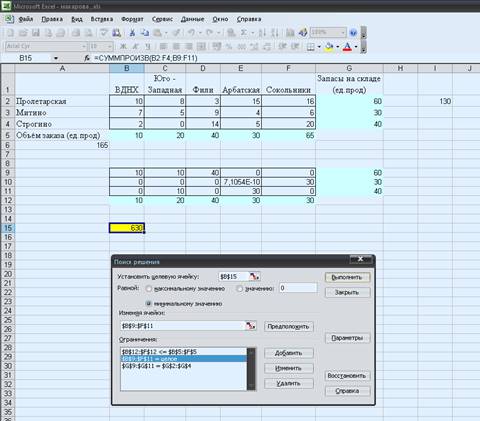
Вводим
параметры
Нажимаем ОК и Выполнить, сохраняем найденное
решение
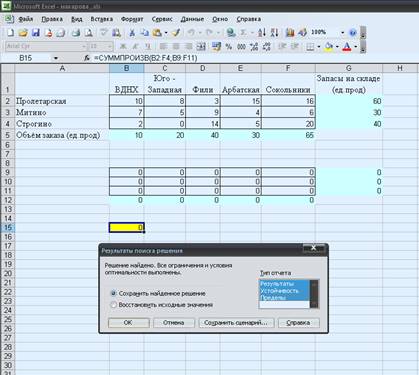
Вывод: транспортные издержки могут
быть минимальны и составлять 630 ден.ед. при следующем плане перевозок
|
10
|
10
|
40
|
0
|
0
|
|
0
|
0
|
0
|
0
|
30
|
|
0
|
10
|
0
|
30
|
0
|
Задача
№ 4
Промышленная группа предприятий (холдинг) выпускает продукцию трех видов,
при этом каждое из трех предприятий группы специализируется на выпуске
продукции одного вида: первое предприятие специализируется на выпуске продукции
первого вида, второе предприятие - продукции второго вида; третье предприятие -
продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями
холдинга (идет на внутреннее потребление), остальная часть поставляется за его
пределы (внешним потребителям, является конечным продуктом). Специалистами
управляющей компании получены экономические оценки аij (i=1,2,3; j=1,2,3) элементов технологической
матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов
yi
вектора конечной продукции Y.
Требуется:
1) Проверить
продуктивность технологической матрицы A=(аij) (матрицы коэффициентов прямых материальных затрат).
2) Построить
баланс (заполнить таблицу) производства
и распределения продукции предприятий холдинга.
Таблица 1
|
Вариант
|
Для первой строки
|
Для второй строки
|
Для третьей строки
|
|
№
|
1А
|
2А
|
3А
|
4А
|
1Б
|
2Б
|
3Б
|
4Б
|
1В
|
2В
|
3В
|
4В
|
|
4
|
0,1
|
0,0
|
0,1
|
100
|
0,1
|
0,0
|
0,2
|
300
|
0,2
|
0,1
|
0,0
|
160
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2
|
Предприятия
(виды продукции)
|
Коэффициенты прямых затрат аi j
|
Конечный
продукт Y
|
|
1
|
2
|
3
|
|
1
2
3
|
1А
1Б
1В
|
2А
2Б
2В
|
3А
3Б
3В
|
4А
4Б
4В
|
Решение
Вводим исходные данные в ячейки В2:D4
|
|
0,1
|
0
|
0,1
|
|
А
=
|
0,1
|
0
|
0,2
|
|
|
0,2
|
0,1
|
0
|
Вводим единичную матрицу
Матрица (Е-А) равна
|
Е-А
|
0,9
|
0
|
-0,1
|
|
|
-0,1
|
1
|
-0,2
|
|
|
-0,2
|
-0,1
|
1
|
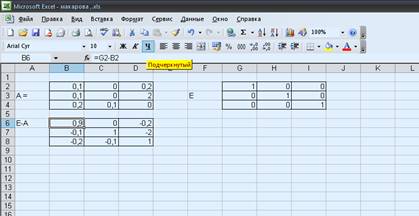
Найдем матрицу (Е-А)-1, которая является обратной
матрице (Е-А) с помощью функции =МОБР и в массив введем значение (B6:D8)
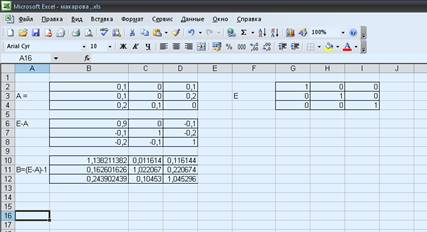
Матрица (Е-А) продуктивна т.к. существует обратная матрица
(Е-А)-1 ≥ 0
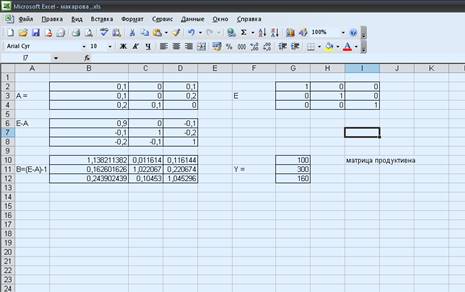
Х = (Е-А)-1 * Y,
находим с помощью функции =МУМНОЖ введя в массив (B10:D12;G10:G12)
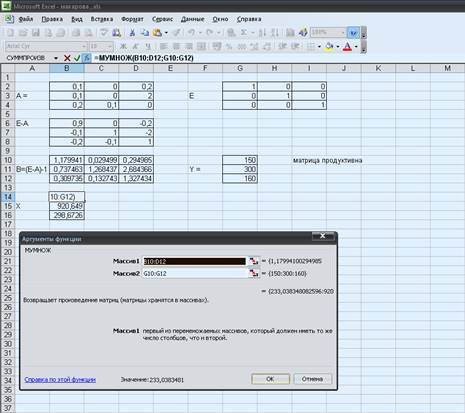
Распределение продукции между
предприятиями на внутреннее потребление определяем из соотношения:
Х11 = а11 * х1 =B2*$B$14
Х12 = а12* х2 =C2*$B$15
Х13 = а13 * х3 =D2*$B$16
Х21 = а21 * х1 =B3*$B$14
…
Получаем
|
13,58885017
|
0
|
22,29965
|
|
13,58885017
|
0
|
44,5993
|
|
27,17770035
|
35,81882
|
0
|
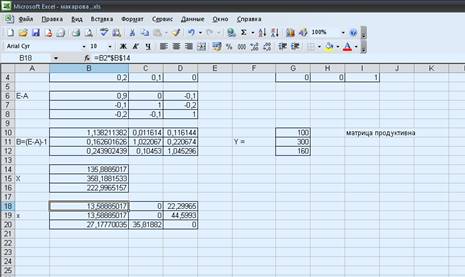
Условно чистая продукция:
Z1 = х1- (х11 + х21 + х31) = 135 – (13,5 + 13,5 + 27) = 81
=B14-(B18+B19+B20);
Z2 = х2- (х12 + х22 + х32) = 358-35 = 323 =B15-(C18+C19+C20);
Z3 =
х3- (х13 + х23 + х33) = 223- (23 + 44) = 156 =B16-(D18+D19+D20).
Валовая продукция:
|
|
135,8885017
|
|
Х
|
358,1881533
|
|
|
222,9965157
|
Межпродуктивный баланс производства и распределения
продукции:
|
Производящие предприятия
|
Потребляющие
п/п
|
конечный
продукт
|
|
1
|
2
|
3
|
|
1
|
13,58885
|
0
|
22,29965
|
100
|
|
2
|
13,58885
|
0
|
44,5993
|
300
|
|
3
|
27,1777
|
35,81882
|
0
|
160
|
|
Условно
чистая продукция
|
81,5331
|
322,3693
|
156,0976
|
560
|
|
Валовая
продукция
|
135,8885
|
358,1882
|
222,9965
|
717,073171
|
Задача
№ 5
В течение девяти последовательных недель фиксировался
спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании.
|
Номер варианта
|
Номер наблюдения ( t = 1,2,…,9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
4
|
30
|
28
|
33
|
37
|
40
|
42
|
44
|
49
|
47
|
Требуется:
1) Проверить наличие
аномальных наблюдений.
2) Построить линейную
модель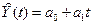 
, параметры которой
оценить МНК (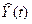
- расчетные,
смоделированные значения временного ряда).
4) Построить адаптивную
модель Брауна[1] 
с параметром сглаживания
a= 0,4 и a= 0,7; выбрать лучшее
значение параметра сглаживания α.
5) Оценить адекватность построенных
моделей, используя свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения (при использовании R/S-критерия взять
табулированные границы 2,7—3,7).
6) Оценить точность моделей
на основе использования средней относительной ошибки аппроксимации.
7) По двум построенным
моделям осуществить прогноз спроса на следующие две
недели (доверительный интервал прогноза
рассчитать при доверительной вероятности р = 70%).
8) Фактические значения
показателя, результаты моделирования и прогнозирования представить графически.
Решение
Вводим исходные данные
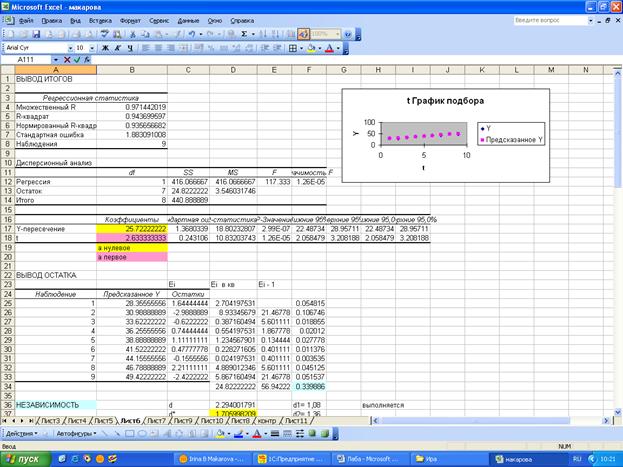
Проводим проверку адекватности
модели: на независимость, нормальность и случайность. Все эти критерии
выполняются и поэтому модель признается адекватной.
Вывели уровень точности, он равен
3,7, что является хорошим уровнем точности Еотн =F34/9*100
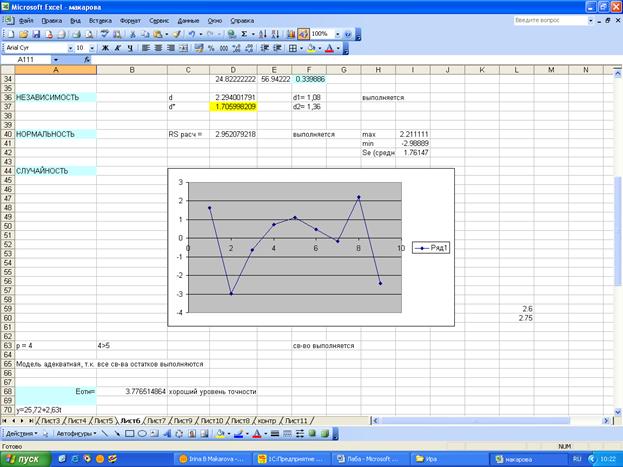
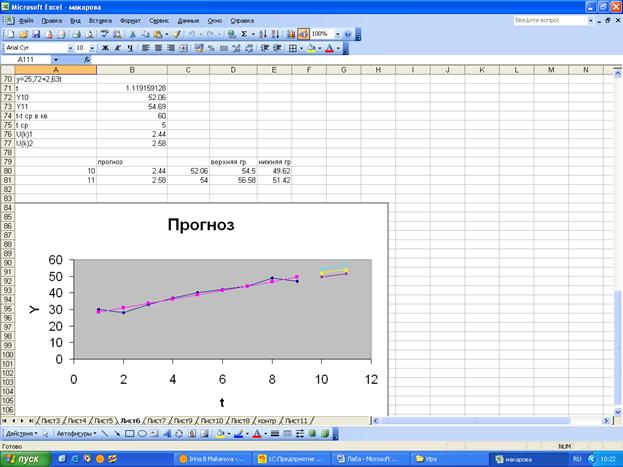
Строим график линейной модели и точечный и интервальный
прогноз
|
|
прогноз
|
|
верхняя
гр
|
нижняя
гр
|
|
10
|
2,44
|
52,06
|
54,5
|
49,62
|
|
11
|
2,58
|
54
|
56,58
|
51,42
|
