Задача 1
Решить
графическим методом типовую задачу оптимизации.
Совхоз для кормления животных использует
два вида корма. В дневном рационе должно содержаться не менее 6 единиц
питательного вещества А и не менее 12
единиц питательного вещества В.
Какое количество корма надо
расходовать ежедневно на одно животное, чтобы затраты были минимальными?
Использовать данные таблицы.
|
Питательное
вещество
|
Количество питательных
веществ в 1 кг корма
|
|
|
1
|
2
|
|
А
В
|
2 2
|
1 4
|
|
Цена 1
кг корма, тыс. руб.
|
0,2
|
0,3
|
Построить экономико-математическую модель
задачи, дать необходимые комментарии к ее элементам и получить решение
графическим методом. Что произойдет, если
решать задачу на минимум, и почему?
Решение.
1)Построение экономико-математической модели задачи
Введем переменные : X1-
количество корма 1, X2 - количество корма 2 (в кг).
Целевая функция в данном случае
затраты на корма обоих видов. Требуется найти такое распределение кормов обоих
видов, чтобы суммарные затраты на покупку кормов были минимальны. При этом
значения переменных должны находиться в
области допустимых решений.
Целевая функция задачи :
f(x) = 0,2X1 + 0,3Х2
Найдём минимум целевой функции.
Область допустимых решений (ОДР)
задачи, согласно условию:
2X1 + Х2 ≥6
X≥0 Х2≥0
2X1 + 4Х2≥12
2)
Построим область допустимых решений (ОДР) задачи.
Условия неотрицательности
переменных означают, что область решений будет лежат в первой четверти Декартовой системы координат.
Функциональные ограничения
(неравенства) определяют область, являющуюся пересечением нижних полуплоскостей с граничными
прямыми и осями координат :
2X1 + Х2 = 6
2X1 + 4Х2 = 12
Пересечение указанных
полуплоскостей в первой четверти представляет собой область АВС (заштрихованная область для всех
ограничений задачи ОДР).
3) Для
определения направления движения к оптимуму построим вектор-градиент, соединив
его вершину с началом координат О (0, 0).
Строим градиент функции - вектор,
показывающий направление возрастания функции f(x).
С=grad(f)= (δf/δx1; δf/δx2) = ( 0,2; 0,3)
4) Построим
некоторую линию уровня .
Пусть, например, а = 0. На эскизе
такой линии уровня отвечает прямая ОХ, перпендикулярная
вектор-градиенту.
0,2 X1+ 0,3 X2 = 0
5) При максимизации
целевой функции (ЦФ) необходимо перемещать линию уровня ОХ в направлении
вектор - градиента, а при минимизации
- в противоположном направлении. Предельной
точкой при таком движении линии уровня ОХ является точка В - крайняя точка (вершина) ОДР (по - другому называемой
многоугольником планов). Далее она (линия уровня) уже не пересекает
единственную точку ОДР (так как область неограниченна сверху).
6)Определим
координаты точки В, являющейся точкой пересечения граничных прямых , решив
систему уравнений :
2*X1+ Х2=6
2*X1 + 4*Х2 = 12
Точка 0( 0; 0 ) - точка начала координат.
Получаем точку В (2;
2) - вершину многоугольника (сектора) планов.
7) Точка В является
так называемым оптимальным планом. В точке В целевая функция принимает свое минимальное значение при заданной системе ограничений.
Эта точка отвечает минимально возможным
затратам на корма при заданной ОДР. При
заданной ОДР отсутствует точка максимума для целевой функции Смысл данного
факта: затраты на корма при данной ОДР никак не ограничиваются (хотя в
реальных случаях такая ситуация невозможна). Таким
образом, целевая функция в задаче линейного программирования принимает, при
заданной системе ограничений :
минимальное значение-min(f)=f(В)=0,2*2 + 0,3 *2 = 1. (тыс.
руб).
максимальное значение - отсутствует (функция неограниченна
сверху на ОДР). С помощью надстройки ЕХСЕL «Поиск решения" минимум
целевой функции, также как и при использовании графического метода. Максимум
найти не удается (сообщается, что
результат не сходится); в таблице помещено только одно из возможных значений.
Ответ:
максимального значения - нет (ОДР неограничен сверху);
min( x) = (2; 2); min(f)= 1 (тысяч денежных единиц).
Графическое решение
B(min)
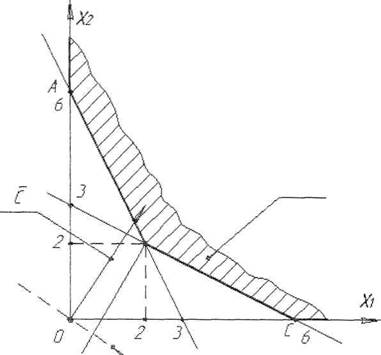 2X1+X2 =
6
2X1+X2 =
6
0,2 X1
+0,3 X2 = 0
Применение
надстройки ЕХСЕL " Поиск
решения
Переменные
|
|
X1
|
Х2
|
Значе ние ЦФ
|
|
Значе ние
|
100
|
100
|
|
|
Коэффи циенты в ЦФ
|
0,2
|
0,3
|
50
|
Нахожденимаксимума
функции
Ограничения
|
|
|
|
левая часть
|
знак
|
правая
часть
|
|
Условие1
|
2
|
1
|
300
|
>=
|
6
|
|
Условие2
|
2
|
4
|
600
|
>=
|
12
|
Переменные
|
|
Х1
|
Х2
|
Значе ние ЦФ
|
|
Значение
|
2
|
2
|
|
|
Коэффи циенты в ЦФ
|
0,2
|
0,3
|
1
|
Ограничения
|
|
|
|
левая часть
|
знак
|
правая часть
|
|
условие 1
|
2
|
1
|
6
|
>=
|
6
|
|
условие 2
|
2
|
4
|
12
|
>=
|
12
|
Нахождениминимума
функции
Задача 2
Использование аппарата теории двойственности для
экономико-математического анализа оптимального плана задачи линейного
программирования.
2.2. Для изготовления четырех видов продукции используют три вида сырья.
Запасы сырья, нормы его расхода и цены
реализации единицы каждого вида продукции приведены в таблице.
|
Тип сырья
|
Нормы расхода сырья на одно
изделие
|
Запасы сырья
|
|
|
А
|
Б
|
В
|
Г
|
|
|
I
|
1
|
0
|
2
|
1
|
180
|
|
II
|
0
|
1
|
3
|
2
|
210
|
|
III
|
4
|
2
|
0
|
4
|
800
|
|
Цена изделия
|
9
|
6
|
4
|
7
|
|
Требуется :
1. Сформулировать прямую оптимизационную задачу на
максимум выручки от реализации готовой
продукции, получить оптимальный план выпуска продукции.
2. Сформулировать двойственную
задачу и найти ее оптимальный план с помощью теорем двойственности.
3. Пояснить нулевые значения переменных
в оптимальном плане.
4. На основе свойств двойственных
оценок и теорем двойственности:
- проанализировать
использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся
выручка и план выпуска продукции при увеличении запасов сырья II и III видов на 120 и 160 единиц соответственно и уменьшении
на 60 единиц запасов сырья I вида;
- определить целесообразность
включения в план изделия Д ценой 12 единиц, на изготовление которого
расходуется по две единицы каждого вида сырья.
Решение.
1.
Формулировка прямой оптимизационной задачи на максимум выручки от реализации готовой
продукции.
Прямая оптимизационная задача:
Найти такое сочетание объема
выпуска изделий разных видов в программе выпуска (так называемый оптимальный план), при котором выручка от реализации
готовой продукции будет максимальна.
При решении данной задачи
учитывается то, что запасы сырья различных видов, используемых в изготовлении изделий, ограничено.
Целевая функция - выручка от
реализации готовой продукции
f(Х) = 9X1 + 6Х2 + 4X3 + 7Х4
Необходимо найти максимальное
значение целевой функции (при учете ограничений
на запасы сырья различных видов):
mах f(X) = 9Х1+ 6 X2 + 4X3 + 7Х4
Расходы различного сырья на все
изделия
1X1+ 0 X2 + 2 X3 + 1 X4< 180 Расход сырья №1
0X1+ 1X2 + З X3 + 2 X4 < 210 Расход
сырья №2
4X1 + 2 X2 + 0 X3+ 4 X4 < 800 Расход
сырья №3
Расход любого сырья
на все изделия не должен превышать имеющихся запасов сырья. Число изделий - величина неотрицательная (и причем -
целая).
X1 > 0 X2> 0 X3 > 0 X4 > 0
Нахождение
максимума функции
Переменные
|
|
Х1
|
Х2
|
X3
|
Х4
|
Значе ние ЦФ
|
|
Значение
|
95
|
210
|
0
|
0
|
|
|
Коэффициенты в ЦФ
|
9
|
6
|
4
|
7
|
2115
|
Ограничения
|
|
|
|
|
|
Левая часть
|
знак
|
правая
часть
|
|
условие1
|
1
|
0
|
2
|
1
|
95
|
<=
|
180
|
|
условие2
|
0
|
1
|
3
|
2
|
210
|
<=
|
210
|
|
условие3
|
4
|
2
|
0
|
4
|
800
|
<=
|
800
|
Нулевые значения Х3 ,
Х4 означают, что данные изделия (изделия "В" и
"Г")
не включают в оптимальную программу выпуска. Причина
этого в том, что стоимость данных изделий
слишком низка, и имеющиеся ресурсы лучше потратить на изготовление других
изделий (в данном случае - изделий "А" и "Б"). В противном
случае максимального значения стоимости выпускаемой продукции достичь нельзя.
2. Формулировка двойственной задачи и
нахождение ее оптимального плана с помощью теорем двойственности.
Прямая оптимизационная задача
Целевая функция - выручка от
реализации готовой продукции.
f(x) = 9X1 + 6Х2 + 4 Х3
+ 7Х4
Необходимо найти максимальное
значение целевой функции (при учете ограничений
на запасы сырья различных видов):
mах f(x) = 9X1+ 6Х2 + 4Х3+
7Х4
Расходы различного
сырья на все изделия
1X1+ 0X2+ 2X3+ 1X4 ≤ 180 Расход
сырья №1
0X1 + 1Х2 + ЗХ3
+ 2Х4≤
210 Расход сырья №2
4X1+ 2Х2 + ОХ3
+ 4Х4 < 800 Расход сырья №3
Расход
любого сырья на все изделия не должен превышать имеющихся запасов сырья.
Число изделий - величина
неотрицательная (и причем - целая).
X1 > 0 Х2 > 0 Х3> 0 Х4> 0
Оптимальный план:

 95
95
X = 210
0
0
Значение целевой функции на
данном плане : mах f(x) = 2115
Проверим, как удовлетворяет
система функциональных ограничений
оптимальному плану.
1*95 + 0*210 + 2 *0+1*0
≤ 180 1*95 + 0*210 + 2*0 + 1 • 0 = 95 < 180
0*95 +1*210 + 3*0 + 2*0≤
210 0*95 + 1*210 + 3*0 + 2*0 = 210
4*95 +
2*210 +0*0 + 4*0≤ 800 4*95
+ 2*210 + 0*0 + 4*0 = 800
Двойственная
задача
Целевая функция -
"внутренняя" стоимость сырья (или, лучше сказать - нормы расхода сырья, но - в ценовом выражении).
g(Y) = 180y1+ 210у2 + 800у3
Необходимо найти минимальное значение
целевой функции (при учете ограничений на
запасы сырья различных видов):
min g(У) = 180у1+210у2 + 800у3
Таким образом, расход сырья на
выпускаемую продукцию должен быть минимален.
Расходы сырья (всех видов) на
изделия :
1y1 +0у2 + 4у3 ≥ 9 на изделие А
0y1 +1у2+2у3≥6 на изделие Б
2y1+3у2+0у3≥4 на изделие В
1y1+2у2+4у3≥7
на
изделиеГ
Расход сырья -
величина неотрицательная:
y1 >
0 y2 > 0 у3 > О
"Внутренняя" стоимость сырья
(цена сырья) называется так потому, что не имеет ничего общего с рыночной ценой сырья, по которому его можно купить или
продать. "Внутренние" же цены (стоимости) - определяются
только из решения задачи.
Для нахождения оценок используем вторую теорему
двойственности. Так как ограничение №1 в
системе ограничений прямой оптимизационной задачи выполняется как
строгое неравенство, то у1 = 0.
Так как X1>0 и Х2>
0, то : 1у1 + 0у2 + 4у3-
9 = 0
0у1 + 1у2 + 2у3 - 6 = 0
Таким образом, для получения
двойственных оценок имеем систему линейных уравнений
у1=0 0*у2 + 4*у3-9=0
1*у1+0*у2
+ 4*у3 = 9 или 0*у2 + 4*у3-9=0
0*y1+1*y2+2*y3=6 1*y2+2*y3=6
Решим систему методом Крамера.

 Вычислим
определители метода:
Вычислим
определители метода:



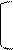





 0 4 9 4
0 4 9 4
Δ=
1
2 =-4 Δ1= 6 2 =18-24=-6 Δ2= 0 9 =-9
1 6
Определим неизвестные:
y1= Δ1/ Δ=-6/-4=1,5
y2= Δ2/ Δ1=-9/-6=1,5
Таким образом, оптимальный
план двойственной задачи:
0
Y= 1,5

 2,25
2,25
Значение целевой
функции: min g(Y)=180*0+210*1,5+800*2,25=2115
К тому же выполняется условие равенства экстремальных
значений двойственных задач (согласно
теореме двойственности) :
max f(x)=min
g(Y)=2115
Нахождение
минимума функции
|
|
У1
|
У2
|
УЗ
|
Значение ЦФ
|
|
Значение
|
0
|
1,5
|
2,25
|
|
|
Коэффициенты в ЦФ
|
180
|
210
|
800
|
2115
|
Ограничения
|
|
|
|
|
левая
часть
|
знак
|
правая часть
|
|
условие
1
|
1
|
0
|
4
|
9
|
>=
|
9
|
|
условие
2
|
0
|
1
|
2
|
6
|
>=
|
6
|
|
условие
3
|
2
|
3
|
0
|
4,5
|
>=
|
4
|
|
условие
4
|
1
|
2
|
4
|
12
|
>=
|
7
|
3.Нулевые значения Х3 , Х4
означают, что данные изделия (изделия "В" и "Г") не включают в оптимальную программу выпуска. Причина
этого в том, что стоимость данных изделий
слишком низка, и имеющиеся ресурсы лучше потратить на изготовление других
изделий (в данном случае - изделий "А" и "Б"). В противном
случае максимального значения стоимости выпускаемой продукции достичь нельзя. Нулевое значение У1 означает, что
данный ресурс (тип сырья I) не полностью используется при производстве
продукции по оптимальному плану основной задачи.
4. Анализы на основе
свойств двойственных оценок и теорем двойственности
4.1.
Анализ использования ресурсов в оптимальном плане исходной задачи.
Оптимальный план двойственной задачи :
У=(0; 1,5;2,25)
Оптимальный план двойственной
задачи содержит "внутренние" стоимости сырья, нaзываемые
также оценками используемых видов сырья (или - ресурсов). Если в оптимальном
плане двойственной задачи величина оценки ресурса - больше нуля (положительная), то данный ресурс полностью
используется при производстве продукции по оптимальному плану основной
(прямой) задачи. Если в оптимальном плане двойственной задачи величина оценки
ресурса - равна нулю, то данный ресурс не
полностью используется при производстве продукции по оптимальному плану
основной задачи. Таким образом, в данном
случае при производстве продукции по оптимальному плану ресурсы №2 и №3 используются
полностью, а ресурс № 1 - не полностью. Остаток ресурса №1 можно узнать, подставив значения оптимального плана
прямой задачи в ограничение № 1 прямой задачи (отражающей запасы сырья
№1)
1X1+0X2 + 2X3 + 1Х4 ≤180
1*95 +
0*210 +2*0+1*0≤180 95 ≤ 180
Остаток ресурса №1, таким образом, равен 85 (180 - 95
= 85). Ресурс №1 является недефицитным. Его недефицитность в данном случае
объясняется не неограниченностью его запасов (так как запасы ограничены).
Недефицитность обуславливается невозможностью его полного использования в оптимальном плане, тем, что расход этого ресурса
не ограничивает величину плана, так расход меньше запаса. Ресурсы №2 и №3 являются дефицитными. Они
полностью используются в оптимальном плане, и план производства -
ограничивается (лимитируется) запасами этих ресурсов. Количественные
величины ненулевых оценок характеризуют ценность соответствующих дефицитных ресурсов. Чем больше величина оценки, тем
острее дефицитность ресурса. Следовательно, тем больше выгода в увеличении
запасов этого ресурса (из-за того, что значение стоимости продукции,
или, вообще говоря, целевой функции прямой задачи, увеличится сильнее). Таким образом, ресурс № 3 (у3 = 2,25)
- более дефицитный и ценный, чем ресурс № 2 (у2 = 1,5). Размер его запаса сильнее влияет на суммарную
стоимость продукции, выпускаемой по оптимальному плану.
4.2.
Определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья II и III видов на 120 и 160
единиц соответственно и уменьшении на 60 единиц запасов сырья I вида.
Нахождение максимума функции
Переменные
|
|
Х1
|
Х2
|
X3
|
Х4
|
Значение ЦФ
|
|
Значение
|
75
|
330
|
0
|
0
|
|
|
Коэффициенты в ЦФ
|
9
|
6
|
4
|
7
|
2655
|
Ограничения
|
|
|
|
|
|
левая часть
|
знак
|
правая часть
|
|
условие 1
|
1
|
0
|
2
|
1
|
75
|
<=
|
120
|
|
условие 2
|
0
|
1
|
3
|
2
|
330
|
<=
|
330
|
|
условие 3
|
4
|
2
|
0
|
4
|
960
|
<=
|
960
|
Оптимальный план : X = (75; 330; 0; 0 )
Суммарная стоимость продукции
: mаx f(Х) = f(75; 330;
0; 0 ) = 2655
Как видно из таблицы ЕХСЕl- с результатами расчёта,
сокращение объема ресурса № 1 и
увеличение объемов ресурсов №2 и №3 позволяет увеличить суммарную выручку. Однако в структуре номенклатуры оптимального
плана выпуска продукции (при котором выручка максимальна) - нет
изменений. По - прежнему в план входят изделия "А" и "Б",
но не входят изделия "В" и "Г" (Х3 и Х4).Причина этого - прежняя (цена изделий
"В" и "Г" слишком низка). Поэтому ресурсы расходуют на те изделия, производство
которых выгодно. Также нужно
заметить, что в оптимальном плане снизилось число изготавливаемых изделий
"А" (75 вместо 95), зато возросло число изделий "Б" (330
вместо 210). Таким образом, данное
изменение запасов ресурсов увеличивает суммарную выручку.
4.3.
Определить целесообразность включения в план изделия "Д" ценой 10
ед., на изготовление которого расходуется по две единицы
каждого вида сырья.
В таблице ЕХСЕL добавим еще одну переменную, отражающую данные о новом изделии "Д". Также
надо внести коррективы в условия (ограничения),
чтобы учесть о количестве ресурсов, расходуемых на производство изделия
"Д".
Нахождение максимума функции
Переменные
|
|
Х1
|
Х2
|
X3
|
Х4
|
Х5
|
Значение ЦФ
|
|
Значение
|
112
|
142
|
0
|
0
|
34
|
|
|
Коэффициенты в ЦФ
|
9
|
6
|
4
|
7
|
12
|
2268
|
Ограничения
|
|
|
|
|
|
|
левая часть
|
знак
|
правая
часть
|
|
условие 1
|
1
|
0
|
2
|
1
|
2
|
180
|
<=
|
180
|
|
условие 2
|
0
|
1
|
3
|
2
|
2
|
210
|
<=
|
210
|
|
условие 3
|
4
|
2
|
0
|
4
|
2
|
800
|
<=
|
800
|
Оптимальный план :X=(112;142;0;0;34)
Суммарная стоимость
продукции : mах f(Х) =f ( 112; 142; 0; 0; 34) =2268
Как видно из таблицы ЕХСЕL с
результатами расчёта, введение в план изделия "Д" позволяет увеличить
суммарную выручку (по сравнению с ситуацией, когда производятся изделия только четырех видов :
"А", "Б", "В", "Г"). В структуре
номенклатуры оптимального плана выпуска продукции (при котором стоимость
продукции максимальна) - произошли изменения. В оптимальный план добавляется
изделие "Д" (обозначаемое какХ5 ). Однако по - прежнему в план входят изделия "А" и
"Б", но не входят изделия "В" и "Г" (Х3
и Х4). И причина этого - прежняя (цена
изделий "В" и "Г" слишком низка). Поэтому ресурсы расходуют на те изделия, производство которых
выгодно. В том числе и на изделие "Д", включённое в план. Также нужно заметить, что в оптимальном плане
возросло число изготавливаемых изделий "А" (112 вместо 95),
зато снизилось число изделий "Б" (142 вместо 210). Следовательно, данное изделие
("Д") целесообразно включать
в план.
Задача 3
Построение баланса производства и распределения продукции предприятий с использованием
балансового метода планирования и модели Леонтьева.
Промышленная группа предприятий
(холдинг) выпускает продукцию трех видов,
при этом каждое из трех
предприятий группы специализируется на выпуске продукции одного вида: первое предприятие
специализируется на выпуске продукции первого вида, второе предприятие -
продукции второго вида, третье
предприятие - продукции третьего вида. Часть
выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть
поставляется за его пределы (внешним
потребителям, являясь конечным продуктом). Специалистами управляющей компании получены экономические оценки аij(i= 1, 2, 3;j= 1,
2, 3 ) элементов технологической матрицы А
(норм расхода, коэффициентов прямых
материальных затрат) и элементов уi, вектора конечной продукции Y.
Требуется :
1 .Проверить продуктивность
технологической матрицы А = (аij) (матрицы коэффициентов прямых материальных затрат);
2.
Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
Исходные данные (вариант № 2)
|
Отрасли
|
Коэффициенты
прямых затрат, аij
|
Конечный
продукт Y
|
|
|
1
|
2
|
3
|
|
|
|
1
|
0
|
0,1
|
0,2
|
180
|
|
|
2
|
0,1
|
0,2
|
0,1
|
200
|
|
|
3
|
0,2
|
0,1
|
0,2
|
200
|
|
Решение





 1. Проверка продуктивности
матрицы коэффициентов прямых материальных затрат (А). Матрица коэффициентов прямых затрат :
1. Проверка продуктивности
матрицы коэффициентов прямых материальных затрат (А). Матрица коэффициентов прямых затрат :
0
0,1 0,2 0
1 2 0
1 2
0,1
0,2 0,1 1
2 1 1
2 1
A=
0,2 0,1
0,2 =0,1* 2 1 2 =1/10* 2 1 2
Оценку продуктивности матрицы
коэффициентов прямых затрат произведем по второму
и четвертому признакам.
1.1 Признак 2: все главные миноры матрицы Е -А
положительны .
Рассмотрим матрицу









 1 0 0 0 0,1
0,2 1
-0,1 -0,2 10
-1 -2
1 0 0 0 0,1
0,2 1
-0,1 -0,2 10
-1 -2
Е –А= 0 1 0 - 0,1
0,2 0,1 = -0,1
0,8 -0,1 =1/10*
-1 8 -1
0
0 1 0,2
0,1 0,2 -0,2
-0,1 0,8 -2
-1 8
Для простоты вычислений вынесем
общий для всех элементов матрицы множитель "за
скобки". Проведем все вычисления с полученной новой матрицей.
Определим главные миноры матрицы:









1 - 1 10
-1 -2
Δ1=10>0 Δ2 = =8-1=7>0 Δ3= -1
8 -1
-1 8 -2
-1 8
Найдём определитель матрицы (по
правилу Саррюса):







 10 -1 -2 10 -1
-2
10 -1 -2 10 -1
-2
Δ3= -1 8 -1 : -1 8 -2
= 10*8*8-2-2-4*8-10-8=640-
4*9-
-2 -1 8 18=586>0
Главные миноры матрицы
положительны.
Главные миноры исходной матрицы
- также положительны, согласно свойствам матриц. Таким образом, матрица коэффициентов прямых затрат (А) - продуктивна.
1.2 Признак 4: максимальное собственное число матрицы
А меньше единицы .







 0
0,1 0,2 1 0 0 0 1 2 1 0 0
0
0,1 0,2 1 0 0 0 1 2 1 0 0
A-λ*E= 0,1
0,2 0,1 - λ* 0
1 0 = 1/10* 1
2 1 - λ* 0
1 0
0,2 0,1
0,2 0 0 1 2
1 2 0
0 1







 0 1 2 1 0 0 0 1 2
0 1 2 1 0 0 0 1 2
A-λ*E= 1/10* 1 2 1 - λ 0 1 0 =
1/10* 1 2 1
2
1 2 0 0 1 2 1 2




 10 0 0
10 0 0
- λ* 0 10 0
0 0 10

 -10*λ 1 2
-10*λ 1 2
A-λ*E=
1/10* 1 2-10*
λ 1
2 1 2-10*
λ
Рассмотрим
характеристическое уравнение: | A-λ* E | = 0




 -10*λ 1 2
-10*λ 1 2
|
A-λ*
E | = 1/103 * 1 2-10* λ 1 =0
2
1 2-10*
λ
-10*λ 1 2
1 2-10*
λ 1 =0
2
1 2-10*
λ





 -10*λ 1 2 -10*λ 1 2
-10*λ 1 2 -10*λ 1 2
: 1 2-10*
λ 1
1 2-10* λ
1
2 1 2-10*
λ
= -10*λ*(2-10*λ)2+2+2-4*(2-10*
λ)+10*λ-(2-10*λ)




-10*λ 1 2
1
2-10λ 1 = -10λ*(2- 10λ)
2+2+2-4*(2-10*λ)+10*λ-(2-
2
1 2-10λ -10*λ)
-10λ 1 2
1 2-10λ 1 =
-1000λ3 +400λ2 +20λ-6
2
1 2-10λ
Таким образом, характеристическое
уравнение:
-1000 λ3 + 400 λ2 + 20λ
- 6 =0
λ3 - 400 * 10-3* λ2 –
20*10-3 * λ + 6 * 10-3 = 0
Корни характеристического уравнения
:
λ 1 =
-0,1273073 < 1
λ 2 = 0,1140435< 1
λ3=0,4132637<1
Таким
образом, максимальное собственное число матрицы A меньше единицы.
Таким образом, матрица
коэффициентов прямых затрат (А) – продуктивна.
2. Построение
баланса производства и распределение продукции отраслей.
Система балансовых уравнений в матричной форме имеет
вид: X = АХ + Y (модель Леонтьева в матричной
форм-модель Леонтьева в матричной форме.
В данном матричном уравнении:
матрица коэффициентов прямых
затрат:
Такобразом,
максимальное собственное





 0 0,1 0,2 0 1 2 0 1 2
0 0,1 0,2 0 1 2 0 1 2
A= 0,1 0,2
0,1 = 0,1* 1
2 1 = 1/10* 1 2 1
0,2 0,1
0,2
2 1 2 2 1 2
Вектор конечной продукции
(конечное потребление и накопление):




Y1 180
Y= Y2 = 200
Y3 200
Вектор валовой продукции (вектор неизвестных):

 X1
X1
X = X2
X3
Выполним эквивалентное
преобразование матричного уравнения.
X=AX+Y X-AX=Y EX-AX=Y (E-A)X=Y
(E-A)X=Y -модель Леонтьева в матричной форме
Таким образом, согласно
свойствам матриц, решение данного уравнения:
X= (E-A)-1*Y или X=BY
B=(E-A)-1 -
матрица коэффициентов полных затрат.
Она является обратной к
матрице (E-A).
Как найдено в пункте 1:
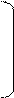
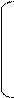
 1 0 0 0 0,1
0,2 1 -0,1
-0,2 10 -1
-2
1 0 0 0 0,1
0,2 1 -0,1
-0,2 10 -1
-2
E-A= 0 1 0 -
0,1 0,2
0,1 = -0,1
0,8 -0,1 =1/10
-1 8
-1 ==
0 0 1 0,2 0,1
0,2 -0,2 -0,1
0,8 -2 -1
8
=D
.

 Поэтому решение матричного
уравнения можно записать в виде:
Поэтому решение матричного
уравнения можно записать в виде:
10
-1 -2 10
-1 -2
1/10 * -1
8 -1 * X= Y -1
8 -1 * X=10* Y
-2 -1
8 -2
-1 8


10 -1
-2 -1
X=10* -1
8 -1 * Y
-2 -1 8
Найдём обратную матрицу методом
преобразований Гаусса.
Составим расширенную матрицу С, состоящую из матрицы О и единичной матрицы Е той же
размерности.
10 -1
-2 1 0
0
C=(D|E)= -1
8 -1 0 1 0
-2 -1
8 0 0 1
10
-1 -2 1
0 0
C=
-1 8
-1 0 1 0 Расширенная
матрица
-2
-1 8 0
0 1
Выполним преобразования
расширенной матрицы методом Гаусса.
1. Поменяем 1 и 2 строки
местами
-1 8 -1 0
1 0
10 -1 -2 1
0 0
-2 -1 8 0
0 1
2. Умножим элементы первой
строки матрицы на -1:
1
- 8 1 0
-1 0
10 -1 -2
0 0 1
-2 -1 8 0
0 1
3. Сложим 2-ую строку
с 1-й, умноженной на (-10); 3-ю с первой, умноженной на 2
1 -8
1 0 -1
0
0 79
-12 1 10 0
0 17
10 0 -2 1
4. Умножим элементы 2 строки матрицы на 1/79
1 -8
1 0
-1 0
0
1 -12/79 1/79
10/79 0
0 -17
10 0 -2 1
5. Сложим 3-ю строку
со 2-ой, умноженной на 17
1 -8
1 0 -1 0
0 1
-12/79 1/79
10/79 0
0 0
586/79 17/79 12/79
1
6. Умножим элементы 3
строки матрицы на 79/586
1 -8 1 0
-1 0
0 1
-12/79 1/79
10/79 0
0 0 1 17/586 12/586
79/586
Таким образом, мы преобразовали
исходную расширенную матрицу к матрице вида ( Р | Т ), где слева стоит верхняя треугольная
матрица Р, а справа - нижняя треугольная матрица Т . (на 5 - м шаге метода Гаусса).
7. Сложим 2-ю строку с 3-ей, умноженной на
12/79, 1-ю с 3-ей, умноженной на (-1)
1 -8 0 -17/586 -598/586 -79/586
0 1 0
10/586 76/586
12/586
0 0 1
17/586 12/586 79/586
8. Сложим 1-ю строку
со 2-ой, умноженной на 8
1 0 0 63/586
10/586 17/586
0
1 0 10/586
76/586 12/586
0 0 1 17/586 12/586
79/586
Таким образом, мы преобразовали исходную расширенную
матрицу к матрице вида ( Е | D-1 ), где слева стоит единичная матрица
Е, а справа - искомая обратная матрица D-1 .
Искомая обратная матрица:



 63/586
10/586 17/586 63 10
17
63/586
10/586 17/586 63 10
17
D=
10/586 76/586 12/586 = 1/
586 * 10
76 12
17/586
12/586 79/586 17 12
79

 Проверка:
Проверка:



 63 10
17 10 -1
-2 1 0 0
63 10
17 10 -1
-2 1 0 0
1/586* 10
76 12 *
-1
8 -1 →
0 1 0
17 12
79 -2
-1 8 0
0 1
D-1* D= Е
Обратная матрица найдена верно.
Определим вектор
валовой продукции (вектор неизвестных):
X1 10
-1 -2 -1 63
10 17 180
X= X2
= 10* -1 8
-1 * Y=10/586
* 10
76 12 * 200 =
X3 -2 -1
8
17 12
79 200
63
10 17 18
= 100/586*
10 76 12
* 20
17 12
79 20


 X1 63
10 17 18 83700/293 285.66
X1 63
10 17 18 83700/293 285.66
X= X2 =
100/586 * 10
76 12 * 20 =
97000/293 = 331.058
X3 17 12
79 20 106300/293 362.799
 285.66
285.66
331.058
X= 362.799
Определим коэффициенты (матрицу коэффициентов)
распределения продукции между предприятиями
на внутреннее потребление, умножая каждый коэффициент прямых затрат (в
матрице А) на соответствующий элемент вектора валовой продукции (для элементов
первой строки - на первый элемент, и так далее). В итоге плановая модель - баланс производства и распределения продукции
предприятий:
Баланс производства и
распределения продукции предприятий
|
Производящие
структуры
|
Потребляющие
структуры
|
Конечный продукт Y
|
Валовой продукт X
|
|
1
|
2
|
3
|
|
1
|
0
|
33,105802
|
75,559727
|
180
|
285,665529
|
|
2
|
28,5665529
|
66,2116041
|
36,2798635
|
200
|
331,0580205
|
|
3
|
57,1331058
|
33,105802
|
72,559727
|
200
|
362,7986348
|
|
Итого
|
85,6996587
|
132,423208
|
181,399317
|
580
|
979,5221843
|
Задача 4
Исследовать
динамику экономического показателя на основе анализа одномерного
временного ряда.
В течение девяти
последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого
показателя приведен ниже в таблице (для варианта 2). Номер показателя : 2
|
Номер наблюдения
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y(t)
|
43
|
47
|
50
|
48
|
54
|
57
|
61
|
59
|
65
|
Требуется :
1 .Проверить наличие аномальных наблюдений.
2.Построить линейную модель Y (t) = а0
+ а1t, параметры
которой оценить
МНК (Y (t) -
расчетные, смоделированные значения временного ряда).
3.Построить адаптивную модель Брауна Y (t) = а0
+ а1t к с
параметром сглаживания ά = 0,4 и ά = 0,7; выбрать лучшее значение параметром
сглаживания.
4.Оценить адекватность построенных моделей, используя
свойства независимости остаточной компоненты, случайности и соответствия
нормальному закону распределения (при использовании R/S - критерия
взять табулированные границы 2,7 - 3,7).
5.Оценить точность моделей на основе использования
средней относительной
ошибки
аппроксимации.
6.По двум построенным моделям осуществить прогноз спроса
на следующие две недели (доверительный интервал прогноза рассчитать при
доверительной вероятности р = 70 %).
7.Фактические значения показателя, результаты моделирования и
прогнозирования представить графически.
Вычисления провести с одним знаком в дробной части.
Основные промежуточные результаты вычислений
представить в таблицах.
Решение
1. Проверка наличия аномальных наблюдений.
Для проверки наличия аномальных наблюдений используем
метод Ирвина.
Вначале определим среднее значение спроса и
среднеквадратическое отклонение. Введем обозначения: i= 1.. .n (n= 9) - номер
наблюдения (аналогично используемому обозначению
t); Yi - значение спроса при наблюдении 1 (или - в i-ю неделю).
Формула для вычисления среднего значения: Yˉ= 1/n*∑* Y i
Формула для вычисления среднеквадратического
отклонения:
S=SY=
√∑ (Yi - Yˉ)2/n-1
Фактически в формуле метода
Ирвина используется так называемое «исправленное» среднеквадратическое отклонение (СКО), являющееся несмещенной оценкой
СКО генеральной совокупности. Для каждого наблюдения (кроме первого по счету)
вычислим расчетное значение критерия Ирвина. Это значение вычисляется по следующей
формуле.
λi=| Yi-
Yi-1|/ SY
Вычисленные расчетные значения критерия Ирвина
сравниваем с табличным значением критерия. Для уровня значимости ά = 0,05
и числа наблюдений n = 10 табличное значение критерия
Ирвина равно 1,5: для числа наблюдений n = 3 оно равно
2,3. Найдем табличное значение критерия Ирвина для числа наблюдений n = 9:
λά(9)=
λά(10)+(( λά(3)- λά(10)/10-3)=1,5+((2,3-1,5)/10-3)=1,5+0,8/7=1,614≈1,6
Если расчетное значение критерия Ирвина для
соответствующего уровня ряда превышает табличное, то этот уровень ряда
считается аномальным. Сравнение расчетных и табличных значений выполним в
расчетной таблице, в столбце «МИ». Если
значение уровня ряда не является аномальным, оно помечается символами
"ОК". Аномальные значения (если такие будут выявлены) помечаются
символом «А». После выявления аномальных уровней ряда нужно определить причины
их возникновения. Если они вызваны ошибками
первого рода, то аномальные уровни заменяются либо простой средней
арифметической двух соседних уровней ряда, либо соответствующими значениями по
кривой аппроксимирующей данный ряд. В данном
случае в ряде значений нет аномальных наблюдений.
2.
Построение линейной модели.
2.1 Находим суммы всех значений t, Y, их
произведений t* Y , а также значений t2, Y2.
2.2.Находим средние значения величин t, Y и их
произведений t* Y .
Для этого просто поделим величины соответствующих
сумм, найденные ранее, на число наблюдений n (то есть на 9).
2.3.Находим дисперсии σ2 t, σ2Y .
Можно найти их, используя квадраты разности между
значением переменной и соответствующим средним значением, т. е. формулы:
_ _
σ2 t =∑
(t- t)2/ n; σ2Y =∑
(Y- Y)2/ n
2.4
Находим коэффициенты уравнения регрессии:
__
_ __
а1=(
tY- t* Y)/ σ2t=(286,11-5*53,78)/6,67=2,58
__ _
а0=
Y - а1*
t = 53,78-2,58*5=40,86
Формулы для определения коэффициентов уравнения
регрессии определяются с использованием метода наименьших квадратов (МНК).
Таким образом, уравнение регрессии имеет вид:
Y= а0+ а1* t;
Y=40,86+2,58* t
Рассчитываем для каждого наблюдения «предсказанное»
(смоделированное) значение отклика (величины показателя) (Y).
 На
основании рассчитанных Y находим значения остатков для каждого наблюдения:
На
основании рассчитанных Y находим значения остатков для каждого наблюдения:
__
εi= Yi - Yi
Решение
задачи с помощью Пакета анализа Ехсеl.
Используем инструмент пакета "Анализ данных" - Регрессия. Вводим
данные для выполнения подпрограммы "Регрессия" и анализируем их
результаты (которые приведены в таблицах).
|
|
Коэффициенты
|
Стандартная ошибка
|
1-статистика
|
|
Y-пересечение
t
|
40,86
|
1,38
|
29,68
|
|
2,58
|
0,24
|
10,56
|
ВЫВОД
ОСТАТКА
|
Наблюдение
|
Предсказанное У
|
Остатки
|
|
1
|
43,44
|
-0,44
|
|
2
|
46,03
|
0,97
|
|
3
|
48,61
|
1,39
|
|
4
|
51,19
|
-3,19
|
|
5
|
53,78
|
0,22
|
|
6
|
56,36
|
0,64
|
|
7
|
58,94
|
2,06
|
|
8
|
61,53
|
-2,53
|
|
9
|
64,11
|
0,89
|
По приведенным данным можно сделать вывод, что
результаты "ручного" расчета (по
формулам) и автоматического расчета совпадают, поскольку коэффициенты
уравнения регрессии - одинаковы.
3 .Построение
адаптивной модели Брауна.
Этап 1: По первым пяти точкам временного
ряда получим начальные оценки параметров модели, используя формулы, полученные
методом наименьших квадратов
а1=∑ ((t- t1 )* (Y(t)- Y1))/ ∑ (t- t1)2;
а0= Y1- а1* t1;
Средние значения для пяти точек вычисляются по
формулам:
_ __
t1=1/5∑ t; Y1=1/5∑
Y(t)
Все вычисления средних значений
и начальных оценок параметров модели выполним
в расчетной таблице.
Этап 2: С помощью начальных
параметров по модели Брауна найдем прогноз на один шаг (k =1):
Yp (t, k )= а0
(t) + а1(t) k.
Этап 3: Расчетное значение Yр (t, k) ряда
сравниваем с фактическим значением Y(t) и вычисляем величину расхождения (ошибки).
Формула для вычисления ошибки (при k = 1):
e (t+1)=Y (t+1)- Yp (t,1)
Этап 4: Корректировка параметров
модели в соответствии с величиной ошибки.
Используются формулы:
а0 (t) = а0 (t-1)+ а1(t-1)+ ά2* e (t);
а1(t) = а1(t-1)+ ά2* e (t).
Здесь ά - параметр сглаживания. Сначала проведем
вычисления при параметре сглаживания, равном 0,4, а затем - равном 0,7.
е (х) - ошибка прогнозирования
уровня Y (t), вычисленная в момент времени
(t +1) на один шаг вперед.
Этап 5: По модели со скорректированными
параметрами а0 и а1 находим прогноз на следующий момент
времени.
Повторяем этапы
построения модели, пока не достигнем значения t = 9 (в данном случае). При достижении t = 9 получаем модель, которую
можно использовать для прогнозирования.
Для параметра сглаживания ά = 0,4
на последнем шаге получаем модель Ур
(N+ k) = 63,6937 +2,948 k , а для ά = 0,7 - модель Ур (N + k) = 64,1103+ +2,437 k.
Необходимо
заметить, что лучшим значением параметра сглаживания является 0,4, поскольку при этом получается меньшая средняя
относительная ошибка аппроксимации и среднеквадратическое отклонение остатков.
Это показывают дальнейшие расчеты.
4.Оценка
адекватности построенных моделей.
4.1 .Проверка случайности остаточной компоненты по
критерию пиков (критерию поворотных
точек).
Уровень последовательности
εt считается максимумом, если он больше двух
рядом стоящих уровней, то есть εt-1 < εt > εt+1 , и минимумом,
если он меньше
обоих соседних
уровней, то есть εt-1 > εt < εt+1. В обоих случаях εt считается поворотной точкой (или пиком).
В случайной выборке размера n математическое ожидание числа точек
поворота
р‾ и дисперсии σр2 выражаются
формулами :
_
р = 2/3*( n-2);
σр2=(16n-29)/90
Критерий случайности остаточной
компоненты (критерий пиков, или поворотных точек)
- выполнение неравенства :
_
р>[р -1,96*√ σр2]
В данном случае критерий
выполняется с 5% - ным уровнем значимости, то есть с доверительной вероятностью 95 % что можно видеть по числу "1,96",
которое стоит рядом со значением
среднеквадратического отклонения.
Данное число (1,96) является табличным значением 1; - статистики Стьюдента
с 5% - м уровнем значимости. Квадратные
скобки в данной формуле означают, что необходимо брать целую часть
получившегося результата. Если неравенство
не выполняется, то следовательно, колебания случайных компонент не являются
случайными. В этом случае трендовая модель считается неадекватной. С помощью средств Ехсеl в расчётной таблице для соответствующих точек
выясним, являются ли они пиками (поворотными
точками). Для поворотных точек в столбце "ТП" (точки поворота)
выводится значение "1", для остальных точек - "О". Таким
образом, всего имеется 4 поворотных точки.
_
р=
2/3*( n-2)= 2/3*(9-2)=4,67;
σр2= (16n-29)/90=(16*9-29)/90=1,28
4>[4,67-1,96*√1,28]= [2,453]=2
Вывод : линейная модель адекватна по критерию случайности
остатков. Для модели Брауна с параметром
сглаживания 0,4 число поворотных точек равно 4, а для параметра 0,7 -
также имеется 4 поворотных точки. Следовательно, модель Брауна также адекватна
по критерию случайности остатков.
4.2.Проверка независимости уровней ряда
остатков по d - критерию. При проверке
независимости значений уровней рада остатков (случайной компоненты), то есть
проверке на отсутствие автокорреляции, определяется отсутствие в ряду систематической составляющей. Проверка может
выполняться по разным критериям, наиболее распространенный из которых d- критерий Дарбина -Уотсона. Расчётное значение данного критерия
вычисляется по формуле :
d =∑[ε(t)- ε(t-1) ]2/∑ ε(t)2
Коэффициент автокорреляции первого порядка
вычисляется по формуле
r(t)= ∑ ε(t)* ε(t-1)/
∑ ε(t)2
Вычислим соответствующие
разности и суммы в расчетной таблице Ехсеl, а затем
вычислим и значение критерия
Для
линейной модели: d=223,9/25,1=8,91
Для модели Брауна d=2,47 (для ά=0,4); d=2,69 (для ά=0,7)
Сравним расчетное значение d
- критерия
линейной модели с верхним критическим
табличным значением
d 2= 1,36 :
d = 8,91 > d 2 = 1,36
Расчетное значение ё - критерия больше верхнего
критического табличного значения d 2=
1,36 . Поэтому можно принять гипотезу о независимости уровней ряда остатков
(отсутствии автокорреляции).
Вывод : линейная модель адекватна по критерию
независимости уровней ряда остатков. Модель
Брауна же в данном случае также адекватна по данному критерию (расчетное
значение критерия больше верхнего критического).
4.3.Проверка
нормальности распределения остаточной компоненты по R/S - критерию с критическими уровнями 2,7 - 3,7.
4.3.1.Для линейной модели.
Расчетное (наблюдаемое) значение RS - критерия равно:
RS=[εmax-εmin]/Sε
где
εmax - максимальный уровень ряда остатков, εmax = 2,06;
εmin- минимальный уровень ряда остатков, εmin=-3,19;
Sε- среднеквадратическое отклонение.
Sε= √∑ ε(t)2/ n-1
Проведем вычисление в таблице и получим расчетное
значение критерия:
RS= 5,25/1,7726=2,962
Расчетное значение RS - критерия попадает в интервал (2,7 - 3,7),
следовательно, выполняется свойство нормального распределения.
Вывод: линейная модель адекватна по нормальности
распределения остаточной компоненты (по RS - критерию).
4.3.2.Для адаптивной модели Брауна
Для
ά = 0,4: εmax = 3,096; εmin = - 2,916 ; Sε = 1,994 ; RS =
3,016
Для
ά = 0,7: εmax = 2,621 ; εmin = - 5,242 ; Sε =
2,996 ; RS = 2,625.
Выводы:
для ά = 0,4 расчетное значение RS -
критерия попадает в интервал (2,7 - 3,7); модель Брауна адекватна по
нормальности распределения остаточной компоненты (по RS - критерию). Для ά = 0,7 - расчетное значение
критерия не попадает в указанный интервал, и модель неадекватна по RS – критерию.
5.Оценка точности
модели по среднему квадратическому отклонению и средней по модулю ошибке.
Оценка точности модели имеет
смысл только для адекватных моделей (для которых все вышеуказанные пункты
проверки дали положительный результат).
В данном случае
линейная модель адекватна по всем этим критериям, поэтому имеет смысл оценить ее точность. Математическое ожидание уровней ряда остатков равно
нулю. Стандартная ошибка прогнозируемого
показателя (среднеквадратическое отклонение от линии тренда):
Sε= √∑ ε(t)2/ n-1= 1,7726
Средняя относительная ошибка
аппроксимации:
Eотн=1/ n*∑ | ε(t)/ Y t|*100%
На
основе проведенных в таблице вычислений:
Eотн=1/9*0,2309*100%=2,57%
Поскольку средняя относительная
ошибка аппроксимации не превосходит 15 % (она значительно меньше), то точность
линейной модели достаточно высока. Однако допустимый
уровень точности модели устанавливает пользователь модели (так как она зависит
от поставленных задач).
Для модели Брауна при ά = 0,4:
Sε= 1,994 ; средняя относительная
ошибка аппроксимации
Еотн= 1/9* 0,2855 *
100 % = 3,17 %.. При ά = 0,7: Sε= 2,996 ;
Еотн = 1/9*0,4049*100 % = 4,50 %.
Поскольку средняя относительная ошибка
аппроксимации не превосходит 15
%, то точность модели Брауна достаточно высока. Однако в данном случае модель Брауна адекватна не по всем этим критериям
(что показано выше).
6. Построение точечного и интервального прогнозов на
следующие две недели
6.1. Построение точечного прогноза для
линейной модели.
Точечный прогноз - это единственное
значение прогнозируемого показателя. Это значение определяется подстановкой в
выбранное уравнение регрессии величины t, соответствующей числу шагов, на
который делается прогноз: t = n + k, где k - число шагов. В
данном случае n = 9, k
= 2 (прогноз на два шага вперёд), следовательно,
t = 9 + 2=11.
Вычислим значение точечного
прогноза, используя найденное уравнение регрессии :
Y (11) = 40,86 + 2,58*11 = 69,278≈69,28.
6.2. Построение интервального прогноза для линейной
модели.
Поскольку точное совпадение
реальных данных в будущем и точечных оценок маловероятно,
то точечный прогноз должен сопровождаться двусторонними границами, указывающими
интервал значений. Причем в этом интервале с достаточной долей вероятности
можно ожидать появления прогнозируемой величины.
Интервальный прогноз - это
установление данного интервала (при соответствующих
условиях). Данный интервал называется доверительным. Расчет доверительных интервалов при
прогнозировании опирается на выводы и формулы теории регрессии. Эти выводы
можно перенести на временные ряды (в том числе экономические), однако с
осторожностью. Стандартная (средняя
квадратическая) ошибка оценки прогнозируемого показателя:
Sε=S Y=√∑(yt-Yt)2/n-m
где yt-
фактическое значение уровня временного ряда для времени t;
Yt - расчётная оценка
соответствующего показателя по модели;
n- количество уровней в исходном ряду (в данном случае n = 9);
m- число параметров модели ( в данном случае m = 1,
так как модель -однопараметрическая).
Формула для доверительного
интервала, в общем случае, имеет вид:
Uy=Y(n+k)±tά* S Y*√1+(1/n)+(3*(n+2*k-1)2)/n(n2-1)
В упрощенном виде: Uy=Y(n+k)± S Y*Kp,
где верхнее значение: Uy(max)= Y(n+k)+ S Y*Kp,
нижнее значение: Uy(min)= Y(n+k)- S Y*Kp.
Расчетный коэффициент: Kp= tά*√1+(1/n)+(3*(n+2*k-1)2)/n(n2-1),
где р = 70 % = 0,7 - вероятность ;
ά = 100 % - 70% = 1 - р = 30 % = 0,3 - уровень
значимости ;
tά - табличное
значение критерия Стьюдента для уровня значимости а и числа
степеней свободы, равного n - 2 .
Величину критерия Стьюдента для
данной величины ошибки и числа наблюдений n= 9(с n -2 =9-2 = 7 степенями свободы tкр (0,30; 7)) находим по таблицам
значений критерия. tкр (0,30; 7)=1,12.
Расчетный коэффициент:
Kp=1,12*√1+1/9+(3*(9+2*2-1)2)/9*(92-1)=1,47
Среднеквадратическое отклонение
вычислено ранее:
Sε=S
Y=√∑(yt-Yt)2/n-m=√∑εt2/
n-1=1,7726
Вычислим значение верхней и
нижней границ доверительного интервала:
верхнее значение: Uy(max)=69,278+1,7726*1,47=71,87
нижнее значение: Uy(min)=69,278-1,7726*1,47=66,68
Таким образом, для линейной
модели доверительный интервал для точечной оценки Y (11) = 69,28 равен
Uy(min) ; Uy(max)) = (66,68; 71,87).
6.3. Построение точечного прогноза для модели Брауна.
Точечный прогноз построен в расчетной таблице, для
ά = 0,4 используем модель Y р (N + k) = 63,6937 +2,948 k , а для ά = 0,7 - модель Yр (N+ k) = 64,1103 +2,437 k . Для ά = 0,4 получаем Y р (11) = 69,59, для
ά = 0,7 - Y р (11) =
68,98.
6.4. Построение интервального
прогноза для модели Брауна.
Для получения интервальных прогнозов для модели Брауна
используется формула:
_ _
U(k)= S Y*tά*√1+1/n+((n+k-t1)/ ∑(t- t1)2)
Вычисления значений интервалов выполним в расчетной
таблице.
Для модели Брауна при ά = 0,4 получаем
U (1) = 5,47;
U (2) = 6,11; для ά = 0,7:U (1)= 8,22; U (2) = 9,19.
Вычислим значение
верхней и нижней границ доверительного интервала при ά =0,4: верхнее значение: Uy (mах) = 69,59 + 6,11 = 75,70$
нижнее значение
: Uy (min) = 69,59 - 6,11 = 63,48.
Таким образом, для модели Брауна при ά = 0,4 доверительный интервал для
точечной оценки Y (11) =
69,59 равен (Uy (min); Uy (mах)) = (63,48; 75,70).
7.1.Графическая иллюстрация фактических данных,
результатов аппроксимации по линейной
модели и результатов прогнозирования.
Чёрными ромбами обозначены точки опытных данных, прозрачными квадратами
- результаты аппроксимации данных с помощью уравнения линейной регрессии,
прозрачный треугольник - точечный прогноз на 2 шага вперед (63,28
«69,3).Соответственно сверху и снизу этой точки находятся соответственно верхняя
и нижняя границы доверительного интервала для этого точечного прогноза,
рассчитанные согласно данных в условии.
80
71,9
30
20
10
0
1 2
3 4
6 7 8 9 1
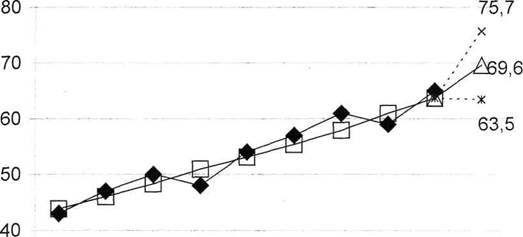
7.2.Графическая иллюстрация фактических данных,
результатов аппроксимации по адаптивной
модели Брауна при ά= 0,4 и результатов прогнозирования.
30 20
10
0
1234567891
Чёрными ромбами обозначены точки опытных
данных, прозрачными квадратами - результаты аппроксимации данных с помощью
адаптивной модели Брауна, прозрачный треугольник - точечный прогноз на 2 шага
вперед (69,6).Соответственно сверху и снизу
этой точки находятся соответственно верхняя и нижняя границы
доверительного интервала для этого точечного прогноза, рассчитанные согласно данных
в условии.
Расчетная
таблица
Линейная модель
|
|
t
|
Y(t)
|
t*Y(t)
|
t2
|
Y(t)2
|
t-t-
|
(t-t-)2
|
Y(t)-Y-
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
1
|
43
|
43
|
1
|
1849
|
-4
|
16
|
-10,8
|
|
|
2
|
47
|
94
|
4
|
2209
|
-3
|
9
|
-6,8
|
|
|
3
|
50
|
150
|
9
|
2500
|
-2
|
4
|
-3,8
|
|
|
4
|
48
|
192
|
16
|
2304
|
-1
|
1
|
-5,8
|
|
|
5
|
54
|
270
|
25
|
2916
|
0
|
0
|
0,2
|
|
|
6
|
57
|
342
|
36
|
3249
|
1
|
1
|
3,2
|
|
|
7
|
61
|
427
|
49
|
3721
|
2
|
4
|
7,2
|
|
|
8
|
59
|
472
|
64
|
3481
|
3
|
9
|
5,2
|
|
|
9
|
65
|
585
|
81
|
4225
|
4
|
16
|
11,2
|
|
∑
|
45
|
484
|
2575
|
285
|
26454
|
0
|
60
|
0
|
|
|
(t-t)(Y(t)-Y)
|
λi
|
МИ
|
Yt
|
εt=Yt-Y
|
ТП
|
εt2
|
εt-εt-1
|
(εt-εt-1)2
|
εtεt-1
|
δi
|
|
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
|
|
43,1
|
-
|
-
|
43,4
|
-0,44
|
-
|
0,2
|
-
|
-
|
-
|
0,0103
|
|
|
20,3
|
0,582
|
OK
|
46
|
0,97
|
0
|
0,9
|
0,7
|
0,6
|
0,2
|
0,0207
|
|
|
7,6
|
0,436
|
OK
|
48,6
|
1,39
|
1
|
1,9
|
1
|
1
|
1,8
|
0,0278
|
|
|
5,8
|
0,291
|
OK
|
51,2
|
-3,19
|
1
|
10,2
|
8,3
|
68,5
|
19,7
|
0,0666
|
|
|
0
|
0,873
|
OK
|
53,8
|
0,22
|
0
|
0
|
-10,2
|
103,1
|
0,5
|
0,0041
|
|
|
3,2
|
0,436
|
OK
|
56,4
|
0,64
|
0
|
0,4
|
0,4
|
0,1
|
0
|
0,0112
|
|
|
14,4
|
0,582
|
OK
|
58,9
|
2,06
|
1
|
4,2
|
3,8
|
14,6
|
1,7
|
0,0337
|
|
|
15,7
|
0,291
|
OK
|
61,5
|
-2,53
|
1
|
6,4
|
2,2
|
4,7
|
27
|
0,0428
|
|
|
44,9
|
0,873
|
OK
|
64,1
|
0,89
|
-
|
0,8
|
-5,6
|
31,4
|
5
|
0,0137
|
|
∑
|
155
|
|
|
484
|
0
|
4
|
25,1
|
0,6
|
223,9
|
56
|
0,2309
|
|
Uy (min)
|
Uy (mах)
|
Y (11)
|
σt2
|
|
66,6807
|
71,8749
|
69,278
|
6,66
|
|
RS
|
Kp
|
S Y
|
|
2,962
|
1,47
|
6,8763
|
|
λά(9)
|
а0
|
а1
|
Sε
|
d
|
Еотн
|
|
1,6
|
40,8611
|
2,583
|
1,77267
|
8,905506
|
2,57%
|
Расчетная таблица
Получение начальных оценок параметров модели
|
|
t
|
Y(t)
|
(t-t-1)2
|
Y(t)-Y-1
|
t-t-1
|
(t-t1)(Y(t)-Y1)
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
1
|
43
|
4
|
-5,4
|
-2
|
10,8
|
|
|
2
|
47
|
1
|
-1,4
|
-1
|
1,4
|
|
|
3
|
50
|
0
|
1,6
|
0
|
0
|
|
|
4
|
48
|
1
|
-0,4
|
1
|
-0,4
|
|
|
5
|
54
|
4
|
5,6
|
2
|
11,2
|
|
∑
|
15
|
242
|
10
|
0
|
0
|
23
|
|
|
3
|
48,4
|
|
а0
|
а1
|
|
|
|
t1
|
Y1
|
|
41,5
|
2,3
|
|
Адаптивная модель
Брауна для ά=0,4
|
t
|
Y(t)
|
а0
|
а1
|
Yp(t)
|
e(t)
|
ТП
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
|
41,5
|
2,3
|
|
|
|
|
1
|
43
|
43,8
|
2,172
|
43,8
|
-0,8
|
|
|
2
|
47
|
45,972
|
2,33648
|
45,972
|
1,028
|
0
|
|
3
|
50
|
48,3085
|
2,60712
|
48,30848
|
1,69152
|
1
|
|
4
|
48
|
50,9156
|
2,14063
|
50,9156
|
-2,9156
|
1
|
|
5
|
54
|
53,0562
|
2,29163
|
53,05623
|
0,94377
|
0
|
|
6
|
57
|
55,3479
|
2,55597
|
55,34786
|
1,65
|
0
|
|
7
|
61
|
57,9038
|
3,05136
|
57,90383
|
3,09616
|
1
|
|
8
|
59
|
60,9552
|
2,73853
|
60,95519
|
-1,95519
|
1
|
|
9
|
65
|
63,6937
|
2,94753
|
63,69372
|
1,30628
|
|
|
10
|
U (1)
|
5,47016
|
Yp(10)
|
66,64125
|
|
4
|
|
11
|
U (2)
|
6,11469
|
Yp(11)
|
69,58879
|
|
|
|
|
tά
|
1,12
|
ά
|
0,4
|
RS
|
3,01558
|
|
εt2
|
εt-εt-1
|
(εt-εt-1)2
|
εtεt-1
|
δi
|
|
8
|
9
|
10
|
11
|
12
|
|
|
|
|
|
|
|
0,64
|
|
|
|
0,018605
|
|
1,056
|
1,828
|
3,341584
|
-0,8224
|
0,021872
|
|
2,86
|
0,66352
|
0,440259
|
1,73888
|
0,03383
|
|
8,5007
|
-4,6071
|
21,22558
|
-4,9318
|
0,060742
|
|
0,8907
|
3,85937
|
14,89476
|
-2,75166
|
0,017477
|
|
2,7295
|
0,70837
|
0,501788
|
1,55924
|
0,028985
|
|
9,5862
|
1,44403
|
2,085216
|
5,1153
|
0,050757
|
|
3,8227
|
-5,0514
|
25,51623
|
-6,0536
|
0,033139
|
|
1,706
|
3,2614
|
10,6372
|
-2,55403
|
0,020097
|
|
Sε
|
d
|
Uy (min)
|
Uy (mах)
|
Еотн
|
ε
(mах)
|
ε
(min)
|
|
1,993566
|
2,473471
|
63,47409
|
75,70348
|
3,17%
|
3,096168
|
-2,915603
|
Адаптивная модель Брауна для ά=0,7
|
t
|
Y(t)
|
а0
|
а1
|
Yp(t)
|
e(t)
|
ТП
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
|
41,5
|
2,3
|
|
|
|
|
1
|
43
|
43,408
|
2,172
|
43,8
|
-0,8
|
|
|
2
|
47
|
46,1412
|
2,33648
|
45,972
|
1,028
|
0
|
|
3
|
50
|
49,4259
|
2,607123
|
48,30848
|
1,69152
|
1
|
|
4
|
48
|
50,4024
|
2,140627
|
50,9156
|
-2,9156
|
1
|
|
5
|
54
|
52,6633
|
2,29163
|
53,05623
|
0,94377
|
0
|
|
6
|
57
|
55,9413
|
2,555972
|
55,34786
|
1,65
|
0
|
|
7
|
61
|
60,0919
|
3,051359
|
57,90383
|
3,09616
|
1
|
|
8
|
59
|
61,6736
|
2,738529
|
60,95519
|
-1,95519
|
1
|
|
9
|
65
|
64,1103
|
2,947533
|
63,69372
|
1,30628
|
|
|
10
|
U (1)
|
8,22084
|
Yp(10)
|
66,54689
|
|
4
|
|
11
|
U (2)
|
9,18947
|
Yp(11)
|
68,98351
|
|
|
|
|
tά
|
1,12
|
ά
|
0,7
|
RS
|
2,624622549
|
|
εt2
|
εt-εt-1
|
(εt-εt-1)2
|
εtεt-1
|
δi
|
|
8
|
9
|
10
|
11
|
12
|
|
|
|
|
|
|
|
0,64
|
|
|
|
0,018605
|
|
2,835856
|
2,484
|
6,170256
|
-1,3472
|
0,03583
|
|
1,267155
|
-0,55832
|
0,311721
|
1,895645
|
0,022514
|
|
22,19019
|
-5,836326
|
34,06271
|
-5,30268
|
0,098138
|
|
6,869871
|
7,33169
|
53,75368
|
-12,34681
|
0,048538
|
|
4,309338
|
-0,545149
|
0,297188
|
5,44101
|
0,036419
|
|
3,170821
|
-0,295214
|
0,087152
|
3,696504
|
0,029191
|
|
27,48289
|
-7,023093
|
49,32383
|
-9,335059
|
0,088854
|
|
3,043603
|
6,987005
|
48,81824
|
-9,145873
|
0,02684
|
|
Sε
|
d
|
Uy (min)
|
Uy (mах)
|
Еотн
|
ε (mах)
|
ε (min)
|
|
2,996033
|
2,685218
|
59,79404
|
78,17299
|
4,50%
|
2,621044
|
-5,242413
|