Задача № 119
Дана система, состоящая из парообразного вещества и твердого
пористого адсорбента, при температуре Т.
1. Постройте изотермы адсорбции и десорбции.
2. Определите тип сорбции, возможность гистерезиса адсорбции
и капиллярной конденсации.
3. Рассчитайте пористость адсорбента по ветви десорбцию, в
случае ее отсутствия – по ветви адсорбции.
4. Рассчитайте радиусы пор по уравнению Томсона-Кельвина и
постройте интегральную и дифференциальную кривые распределения пор адсорбента
по радиусам.
Исходные данные:
- Т = 293 К
- монтмориллонит
- Н2О
|
Р ·
10-2, Па
|
2,34
|
4,68
|
7,03
|
9,35
|
11,7
|
14,0
|
16,4
|
21,0
|
23,0
|
|
А,
моль/кг
|
4,0
|
6,0
|
7,3
|
8,3
|
9,0
|
9,5
|
10,0
|
12,6
|
17,0
|
|
Д,
моль/кг
|
4,0
|
6,0
|
7,3
|
8,3
|
9,0
|
11,0
|
11,6
|
14,0
|
17,0
|
Решение.
1. Изотерма адсорбции – это график зависимости адсорбции паров
воды от давления этих паров. Изотерма десорбции – это график зависимости
десорбции паров воды от давления этих паров (см. рис. 2).
2. При построении графиков, оказалось, что изотерма
адсорбции – нижняя кривая, изотерма десорбции – верхняя кривая не совпадают,
что свидетельствует о наличии явления, называемого гистерезисом.
Явление гистерезиса свидетельствует о том, что
монтмориллонит – пористый адсорбент. Вид сорбции – капиллярная конденсация.
Адсорбция паров воды на монтмориллоните по классификационным признакам является
молекулярной, физико-химической, протекающей на границе газ – твердое тело, по
механизму – полимолекулярная адсорбция.
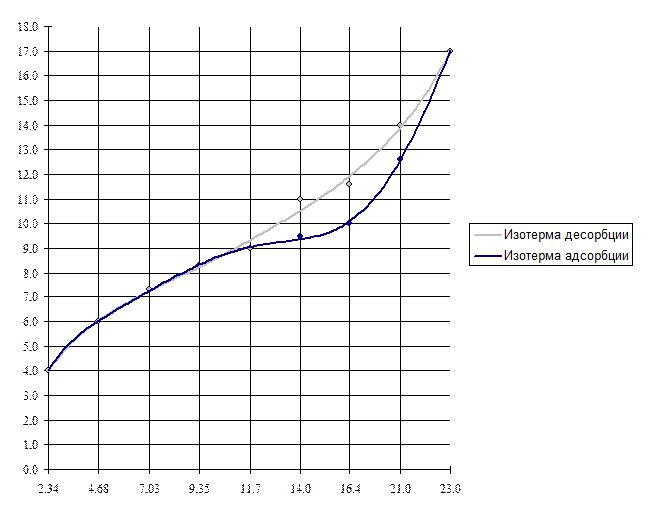
Рис. 2. Изотермы адсорбции и десорбции.
3. Расчет пористости адсорбента и радиусов пор проводим по
следующим формулам:
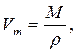
где: Wn – пористость адсорбента, м3/кг;
Д – десорбция, моль/кг;
Vm
– молярный объем молярный объем адсорбата, м3/моль;
М – молярная масса адсорбата, кг/моль;
ρ – плотность адсорбата, кг/м3.
Рассчитываем пористость при различных значениях десорбции паров
воды на монтмориллоните. Для воды находим: ρ = 1000 кг/м3; М =
18·10-3 кг/моль.
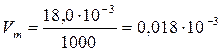м3/моль.
Рассчитаем Wn для Д = 4,0 моль/кг
м3/кг
Аналогично рассчитываем Wn для других значений
десорбции паров воды на монтмориллоните. Рассчитанные величины представим в
виде таблицы (см. таблицу 1).
4. Рассчитаем радиусы пор по уравнению Томсона-Кельвина:
,
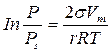где: Р – давление паров адсорбата
при данной температуре, Па;
Рs – давление насыщенных паров
адсорбата при данной температуре, Па;
σ – поверхностное натяжение
адсорбата, Дж/м2;
r – радиус пор адсорбента, м;
R – универсальная газовая постоянная,
Дж/(моль·К);
Т – температура, К.
Для воды находим: σ = 72,5·10-3 Дж/м2;
Рs = 23,4
·10-2 Па.
Рассчитаем r
при Р = 2,34 · 10-2 Па
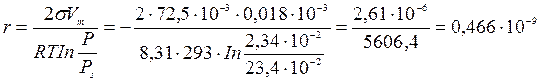м
Аналогично рассчитываем r для других значений десорбции паров
воды на монтмориллоните. Рассчитанные величины представим в виде таблицы (см.
таблицу 1).
Общая пористость адсорбента Wn складывается из объема пор
разных радиусов r.
Чтобы узнать, поры каких радиусов преобладают в адсорбенте, необходимо
построить интегральную (
) и дифференциальную (
) кривые распределения пор по радиусам (см. рис. 3).
Максимумы на дифференциальной кривой распределения пор по радиусам
соответствует радиусу пор, которых больше всего в адсорбенте.
Таблица 1
|
Р ·
10-2, Па
|
2,34
|
4,68
|
7,03
|
9,35
|
11,7
|
14,0
|
16,4
|
21,0
|
23,0
|
|
Wn · 10-3, м3/кг
|
0,072
|
0,108
|
0,131
|
0,149
|
0,162
|
0,198
|
0,209
|
0,252
|
0,306
|
|
r · 10-9, м
|
0,466
|
0,666
|
0,891
|
1,169
|
1,547
|
2,086
|
3,015
|
9,908
|
62,181
|
|
|
0,155
|
0,18
|
0,102
|
0,065
|
0,034
|
0,067
|
0,012
|
0,007
|
0,001
|
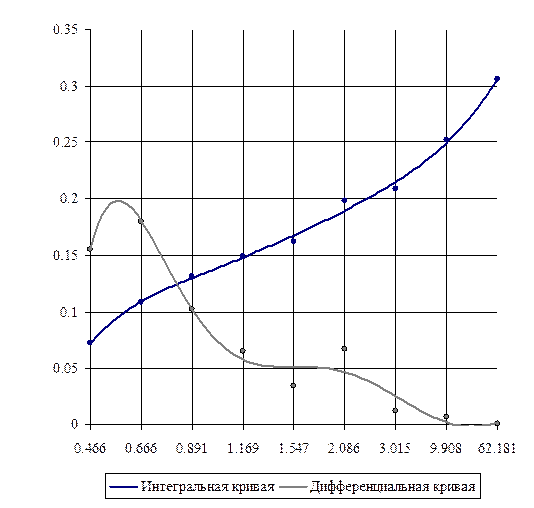
Рис. 3. Интегральная и дифференциальная кривые распределения пор по
радиусам.