МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Филиал в г. Пензе
Контрольная работа
По дисциплине «Финансовая математика»
Вариант № 1
Выполнила: Мещанинова Мария Сергеевна
Факультет: финансово-кредитный
Специальность: финансы и кредит
Курс: 4
Группа: 2
№ личного дела: 05фбб03801
Проверил: Прокофьев Олег Владимирович
Пенза,
2008
Задача № 1
Приведены поквартальные
данные о кредитах от коммерческого банка на жилищное строительство (в условных
единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому
кварталу первого года).
Таблица 1: Данные о кредитах от
коммерческого банка на жилищное строительство за 4 года
|
Квартал
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Данные
|
28
|
36
|
43
|
28
|
31
|
40
|
49
|
30
|
34
|
44
|
52
|
33
|
39
|
48
|
58
|
36
|
Требуется:
1) Построить
адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора,
приняв параметры сглаживания 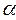 1=0,3;
1=0,3; 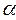 2=0,6;
2=0,6; 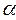 3=0,3.
3=0,3.
2)
Оценить точность построенной модели с использованием
средней относительной ошибки аппроксимации.
3)
Оценить адекватность построенной модели на основе
исследования:
·
случайность остаточной компоненты по критерию
пиков;
·
независимость уровня ряда остатков по d-критерию (критическое
значение d1=1,10
и d2=1,37)и
по первому коэффициенту автокорреляции при критическом значении r1=0,32;
·
нормальности распределения остаточной компоненты
по R/S-критерию с критическими значениями от
3 до 4,21.
4)
Построить точечный прогноз на 4 шага вперед, т.е. на 1
год.
5)
Отразить на графике фактические, расчетные и прогнозные
данные.
Решение:
Будем считать,
что зависимость между компонентами тренд – сезонный временной ряд
мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом
имеет следующий вид:
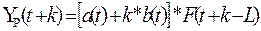
где k – период упреждения.
Уточнение (адаптация к
новому значению параметра времени t) коэффициентов модели
производится с помощью формул:
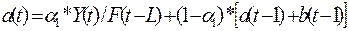
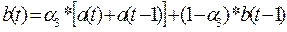
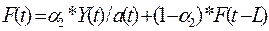
Из
вышеприведенных формул видно, что для расчета a(1) и b(1)
необходимо оценить значение этих коэффициентов для предыдущего периода
времени (т.е. для t=1-1=0).
Значения a(0) и b(0) имеют смысл этих же коэффициентов для четвертого
квартала года, предшествующего коэффициентов четвертого квартала года,
предшествующего первому году, для которого имеются данные.
Для оценки
начальных значений a(0) и b(0) применим линейную модель
к первым восьми значениям Y(t). Линейная модель имеет
вид:
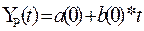
Метод наименьших
квадратов дает возможность определить коэффициенты линейного уравнения a(0) и b(0) по
следующим формулам:
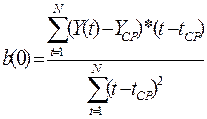
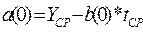
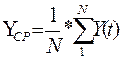
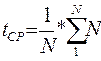
Применим линейную модель к первым 8 значениям ряда,
воспользуемся для этого приведенными выше формулами.
Промежуточные вычисления
приведены ниже в таблице 2:
Таблица 2:Расчетные данные
|
t
|
Y(t)
|
(Y(t)-YCP)
|
(t-tCP)
|
(t-tCP)2
|
(Y(t)-YCP)* (t-tCP)
|
|
1
|
28
|
-7,63
|
-3,50
|
12,25
|
26,71
|
|
2
|
36
|
0,37
|
-2,50
|
6,25
|
-0,92
|
|
3
|
43
|
7,37
|
-1,50
|
2,25
|
-11,06
|
|
4
|
28
|
-7,63
|
-0,50
|
0,25
|
3,82
|
|
5
|
31
|
-4,63
|
0,50
|
0,25
|
-2,32
|
|
6
|
40
|
4,37
|
1,50
|
2,25
|
6,56
|
|
7
|
49
|
13,37
|
2,50
|
6,25
|
33,43
|
|
8
|
30
|
-5,63
|
3,50
|
12,25
|
-19,71
|
|
36
|
285
|
|
|
42,00
|
36,51
|
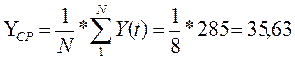
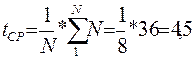
В результате проведенных вычислений
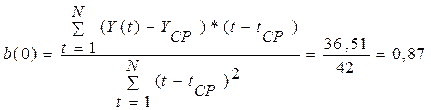
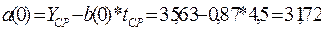
Выше приведенное уравнение
с учетом полученных коэффициентов имеет вид: 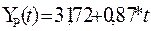 . Из этого уравнения находим расчетные значения
. Из этого уравнения находим расчетные значения 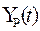 и сопоставляем их с
фактическими значениями (результаты приведены ниже в таблице 3):
и сопоставляем их с
фактическими значениями (результаты приведены ниже в таблице 3):
Таблица 3: сопоставление фактических данных Y(t) и рассчитанных по линейной модели
значений YP(t)
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Y(t)
|
28
|
36
|
43
|
28
|
31
|
40
|
49
|
30
|
|
YP(t)
|
32,59
|
33,46
|
34,33
|
35,2
|
36,07
|
36,94
|
37,81
|
38,68
|
Такое сопоставление позволяет
оценить приближенные значения коэффициентов сезонности I-IV кварталов F(-3),
F(-2), F(-1), и F(0) для года, предшествующего первому
году, по которому имеются данные. Эти значения необходимы для расчета
коэффициентов сезонности первого года F(1), F(2), F(3) и других
параметров модели Хольта-Уинтерса.
Коэффициент сезонности есть отношение фактического значения экономического
показателя к значению, рассчитанному по линейной модели. Поэтому в качестве
оценки коэффициента сезонности I квартала F(-3) может служить отношение фактических и расчетных
значений 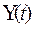 I
квартала первого года, равное Y(1)/YP(1), и такое же отношение
для I квартала второго года (т.е. за V квартал t=5) Y(5)/YP(5). Для окончательной,
более точной, оценки этого коэффициента сезонности можно использовать среднее
арифметическое значение этих двух величин. Аналогично находим оценки
коэффициента сезонности для II, III, IV кварталов.
I
квартала первого года, равное Y(1)/YP(1), и такое же отношение
для I квартала второго года (т.е. за V квартал t=5) Y(5)/YP(5). Для окончательной,
более точной, оценки этого коэффициента сезонности можно использовать среднее
арифметическое значение этих двух величин. Аналогично находим оценки
коэффициента сезонности для II, III, IV кварталов.
F(-3)=[Y(1)/YP(1)+Y(5) /YP(5)]/2=[28/32,59+31/36,07]/2=0,8593
F(-2)=[Y(2)/YP(2)+Y(6) /YP(6)]/2=[36/33,46+40/36,94]/2=1,0794
F(-1)=[Y(3)/YP(3)+Y(7) /YP(7)]/2=[43/34,33+49/37,81]/2=1,2743
F( 0)=[Y(4)/YP(4)+Y(8) /YP(8)]/2=[28/35,20+30/38,68]/2=0,7855
Оценив значения a(0) и b(0), а
также F(-3), F(-2), F(-1) и F(0), можно перейти к
построению адаптивной мультипликативной модели Хольта-Уинтерса.
Используя выше
приведенные уравнения построим модель Хольта-Уинтерса.
Таблица 4: Модель Хольта-Уинтерса
|
t
|
Y(t)
|
a(t)
|
b(t)
|
F(t)
|
YP(t)
|
Абсолютная
погрешность, Е(t)
|
Относительная
погрешность, в %
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
0
|
|
31,72
|
0,87
|
0,7855
|
|
|
|
|
1
|
28
|
32,59
|
0,87
|
0,8592
|
28,00
|
0,00
|
0,00
|
|
2
|
36
|
33,43
|
0,86
|
1,0780
|
36,11
|
-0,11
|
0,32
|
|
3
|
43
|
34,12
|
0,81
|
1,2658
|
43,69
|
-0,69
|
1,61
|
|
4
|
28
|
35,15
|
0,88
|
0,7922
|
27,44
|
0,56
|
2,00
|
|
5
|
31
|
36,04
|
0,88
|
0,8598
|
30,95
|
0,05
|
0,15
|
|
6
|
40
|
36,98
|
0,90
|
1,0803
|
39,80
|
0,20
|
0,50
|
|
7
|
49
|
38,12
|
0,97
|
1,2775
|
47,94
|
1,06
|
2,16
|
|
8
|
30
|
38,73
|
0,86
|
0,7816
|
30,97
|
-0,97
|
3,24
|
|
9
|
34
|
39,58
|
0,86
|
0,8594
|
34,04
|
-0,04
|
0,12
|
|
10
|
44
|
40,52
|
0,88
|
1,0836
|
43,68
|
0,32
|
0,73
|
|
11
|
52
|
41,20
|
0,82
|
1,2683
|
52,90
|
-0,90
|
1,73
|
|
12
|
33
|
42,08
|
0,84
|
0,7832
|
32,84
|
0,16
|
0,47
|
|
13
|
39
|
43,66
|
1,06
|
0,8797
|
36,88
|
2,12
|
5,43
|
|
14
|
48
|
44,59
|
1,02
|
1,0793
|
48,46
|
-0,46
|
0,95
|
|
15
|
58
|
45,65
|
1,03
|
1,2697
|
57,86
|
0,14
|
0,25
|
|
16
|
36
|
46,47
|
0,97
|
0,7781
|
36,56
|
-0,56
|
1,56
|
Для того чтобы
модель была качественной уровни, остаточного ряда Е(t)
(разности Y(t)-YP(t) между фактическими и
расчетными значениями экономического показателя) должны удовлетворять
определенным условиям (точности и адекватности). Для проверки выполнения этих
условий составим таблицу 5.
Проверка точности модели.
Будем считать, что условие точности выполнено, если относительная погрешность
(абсолютное значение отклонения abs{E(t)}, поделенное на фактическое значение Y(t) и выраженное в процентах 100%* abs{E(t)}/ Y(t) в среднем не превышает 5%.
Суммарное значение относительных погрешностей составляет 21,23, что дает
среднюю величину 21,23/16=1,33%.
Проверка условий адекватности.
Для того чтобы модель была адекватной исследуемому
процессу, ряд остатков E(t) должен обладать свойствами
случайности, независимости последовательных уровней, нормальности
распределения.
Проверка случайности уровней. Проверка
случайности уровней остаточной компоненты проводим на основе критерия
поворотных точек. Для этого каждый уровень ряда
E(t) сравниваем с двумя
соседними. Если он больше (либо меньше) обоих соседних уровней, то точка
считается поворотной и в гр. 3 таблицы 5
для этой строки ставится 1, в противном случае в графе 3 ставится 0. В первой и последней строке графы 3 таблицы 5
ставится прочерк или иной знак, так как у этого уровня нет двух соседних
уровней.
Таблица 5: Промежуточные расчеты для
оценки адекватности модели
|
t
|
Отклонение, E(t)
|
Точка поворота
|
Е(t)2
|
[E(t)-E(t-1)]^2
|
E(t)*E(t-1)
|
|
1
|
2
|
3
|
4
|
6
|
7
|
|
1
|
0,00
|
хххх
|
0,00
|
|
|
|
2
|
-0,11
|
0
|
0,01
|
0,01
|
0,00
|
|
3
|
-0,69
|
1
|
0,48
|
0,33
|
0,08
|
|
4
|
0,56
|
1
|
0,31
|
1,56
|
-0,39
|
|
5
|
0,05
|
1
|
0,00
|
0,26
|
0,03
|
|
6
|
0,20
|
0
|
0,04
|
0,02
|
0,01
|
|
7
|
1,06
|
1
|
1,12
|
0,74
|
0,21
|
|
8
|
-0,97
|
1
|
0,94
|
4,13
|
-1,03
|
|
9
|
-0,04
|
0
|
0,00
|
0,87
|
0,04
|
|
10
|
0,32
|
1
|
0,10
|
0,13
|
-0,01
|
|
11
|
-0,90
|
1
|
0,81
|
1,48
|
-0,29
|
|
12
|
0,16
|
0
|
0,02
|
1,11
|
-0,14
|
|
13
|
2,12
|
1
|
4,48
|
3,85
|
0,33
|
|
14
|
-0,46
|
1
|
0,21
|
6,62
|
-0,96
|
|
15
|
0,14
|
1
|
0,02
|
0,36
|
-0,07
|
|
16
|
-0,56
|
хххх
|
0,32
|
0,50
|
-0,08
|
|
Итого
|
0,87
|
10
|
8,88
|
21,98
|
-2,27
|
Общее число
поворотных точек в нашем примере равно p=10. Расчетное значение q:
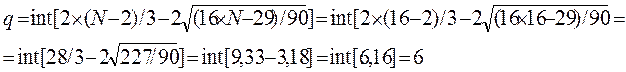
Если количество
поворотных точек p больше q, то условие случайности
выполнено. В нашем случае p=10, q=6,
значит условие случайности уровней ряда остатков выполнено.
Проверка независимости
уровней ряда остатков (отсутствие автокорреляции). Проверку проводим двумя
методами:
- по
d-критерию
Дарбина-Уотсона
- по
первому коэффициенту автокорреляции r(1)
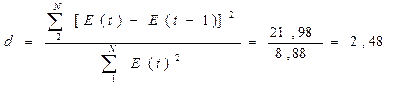
Т.к. полученное значение больше 2,значит имеет место
отрицательная автокорреляция. В таком случае величину d уточняют, вычитая полученное значение
из 4. d=4-2,48=1,52. В нашем случае d1=1,10, а d2=1,37. Т.к. в
нашем случае d2<d<2 (1,37<1,52<2),
следовательно, уровни ряда остатков ряда E(t) независимы.
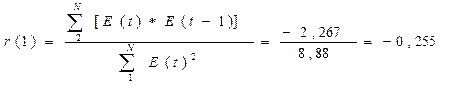
Если модуль рассчитанного значения первого
коэффициента автокорреляции меньше критического значения | r(1) | < rтаб
, то уровни ряда остатков независимы. Для нашей задачи критический уровень rтаб=
0,32.
Имеем:
| r(1) |=-0,255< rтаб= 0,32 –
значит уровни независимы.
Проверка соответствия ряда остатков нормальному
распределению определяем по RS – критерию. Рассчитаем значение RS:
RS=(Emax
– Emin)/S,
где
Emax – максимальное значение уровней ряда остатков E(t);
Emin –минимальное значение уровней ряда остатков E(t) (графа 2, таблица 5);
S – среднее квадратическое отклонение.
Emax = 2,12; Emin = - 0,97;
Emax - Emin = 2,12
– (-0,97) = 3,09
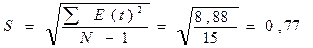
RS=(Emax – Emin)/S=3,09/0,77=4,01
Полученное значение RS сравнивают с табличными значениями, которые зависят от
количества точек N и
уровня значимости. Для N=
16 и 5% уровня значимости значение RS для нормального распределения должно находится в интервале от
3,00 до 4,21.
Так как 3,00<4,01<4,21 полученное значение RS попало в заданный интервал.
Значит, уровни ряда остатков подчиняются нормальному распределению.
Таким образом все условия адекватности и точности
выполнены. Следовательно, можно говорить об удовлетворительном качестве модели
и возможности проведения прогноза показателя YP(t)
на четыре квартала вперед.
Расчет
прогнозных значений.
Составим прогноз на четыре квартала вперед (т.е. на 1
год с t=17 по t=20). Максимальное значение t, для которого могут быть
рассчитаны коэффициенты a(t), b(t) определяются количеством исходных данных и равно 16. Рассчитав
значения a(16), b(16) можно определить
прогнозные значения экономического показателя YP(t). Для t=17
YP(17)=YP(16+1)=[a(16)+1*b(16)]*F(16-+1-4)=[a(16)+1*b(16)]*F(13)=
[46,47+1*0,97]* 0,8797=41,73
Аналогично находим YP(18), YP(19), YP(20):
YP(18)=YP(16+2)=[a(16)+2*b(16)]*F(16-+2-4)=[a(16)+2*b(16)]*F(14)=
[46,47+2*0,97]* 1,0793=52,23
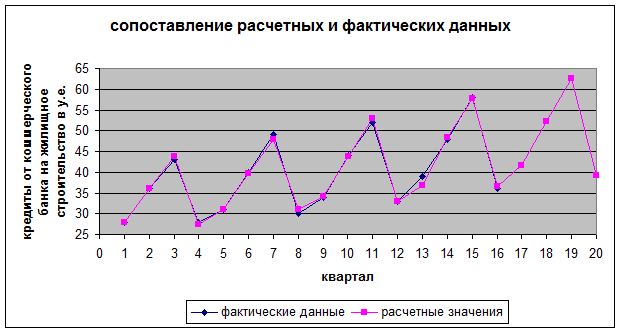
Рисунок 1: сопоставление расчетных и
фактических данных
YP(19)=YP(16+3)=[a(16)+3*b(16)]*F(16-+3-4)=[a(16)+3*b(16)]*F(15)=
[46,47+3*0,97]* 1,2697=62,70
YP(20)=YP(16+4)=[a(16)+4*b(16)]*F(16-+4-4)=[a(16)+1*b(16)]*F(16)=
[46,47+4*0,97]* 0,7781=39,18
На выше приведенном
рисунке 1 проводится сопоставление фактических и расчетных данных. Здесь же
показаны прогнозные значения цены акции на 1 год вперед. Из рисунка видно, что
расчетные данные хорошо согласуются с фактическими, что говорит об
удовлетворительном качестве прогноза.
Задача № 2.
Даны цены (открытия,
максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять
равным пяти дням. Рассчитать:
- экспоненциальную
скользящую среднюю;
- момент;
- скорость
изменения цен;
- индекс
относительной силы;
- %R, %K и %D.
Расчеты
проводить для всех дней, для которых эти расчеты можно выполнить на основании
имеющихся данных.
Таблица 6: Данные о ценах (максимальная, минимальная и
закрытия)
|
Дни
|
Цены
|
|
максимальная
|
минимальная
|
закрытия
|
|
1
|
998
|
970
|
982
|
|
2
|
970
|
922
|
922
|
|
3
|
950
|
884
|
902
|
|
4
|
880
|
823
|
846
|
|
5
|
920
|
842
|
856
|
|
6
|
889
|
840
|
881
|
|
7
|
930
|
865
|
870
|
|
8
|
890
|
847
|
852
|
|
9
|
866
|
800
|
802
|
|
10
|
815
|
680
|
699
|
Решение:
Расчет простой скользящей средней
производится по следующей формуле:
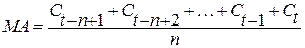
где Сt – цена закрытия в момент времени t.
Вычислив МА для первых пяти дней. Запишем
полученный результат в графы 3 и 4 за пятый день таблицы 7.
Рассчитаем экспоненциальную скользящую
средную по формуле:
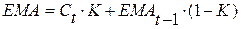
где 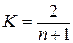
C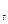 - цена
закрытия t-го дня;
- цена
закрытия t-го дня;
ЕМА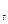 - значение ЕМА текущего дня t.
- значение ЕМА текущего дня t.
ЕМА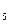 =
=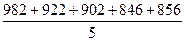 =901,60
=901,60
ЕМА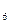 = 881*2/(5+1)+901,60*(1-2/(5+1))=894,73
= 881*2/(5+1)+901,60*(1-2/(5+1))=894,73
ЕМА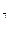 =870*2/(5+1)+894,73*(1-2/(5+1))=886,49
=870*2/(5+1)+894,73*(1-2/(5+1))=886,49
ЕМА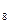 =852*2/(5+1)+886,49*(1-2/(5+1))= 874,99
=852*2/(5+1)+886,49*(1-2/(5+1))= 874,99
ЕМА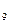 =802*2/(5+1)+ 874,99*(1-2/(5+1))=850,66
=802*2/(5+1)+ 874,99*(1-2/(5+1))=850,66
ЕМА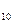 =699*2/(5+1)+850,66*(1-2/(5+1))=800,10
=699*2/(5+1)+850,66*(1-2/(5+1))=800,10
Результаты расчетов простой скользящей средней и
экспоненциальной скользящей средней представлены ниже в таблице 7. График
экспоненциальной скользящей средней представлен на рисунке 2.
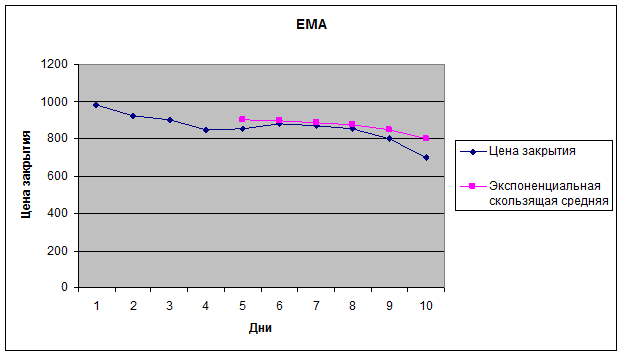
Рисунок 2: Экспоненциальная скользящая средняя.
Пересечения графиков не наблюдается, что
говорит об отсутствии каких-либо сигналов к покупке либо продаже.
Рассчитаем момент по формуле:
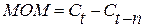
где C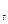 - цена
закрытия t-го дня;
- цена
закрытия t-го дня;
МОМ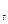 - значение МОМ текущего дня t.
- значение МОМ текущего дня t.
Положительные значения МОМ свидетельствуют об
относительном росте цен, отрицательные – о снижении. Движение графика МОМ вверх
из зоны отрицательных в зону положительных значений в точке пересечения нулевой
линии дает сигнал к покупке (в случае нисходящего тренда ситуация развивается в
обратном направлении).
МОМ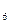 =С
=С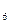 -С
-С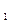 =881-982=-101
=881-982=-101
МОМ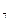 =С
=С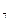 -С
-С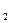 =870-922=-52
=870-922=-52
МОМ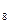 =С
=С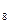 -С
-С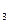 =852-902=-50
=852-902=-50
МОМ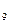 =С
=С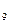 -С
-С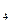 =802-846=-44
=802-846=-44
МОМ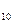 =С
=С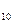 -С
-С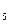 =6999-856=-157
=6999-856=-157
Результаты расчетов момента представлены ниже в
таблице 7. График момента представлен на рисунке 3.
Движение графика момента вверх из зоны отрицательных
значений является слабым сигналом. Начиная с 9 дня график момента опять
направлен вниз в зону отрицательных значений, что свидетельствует о снижении
цен.
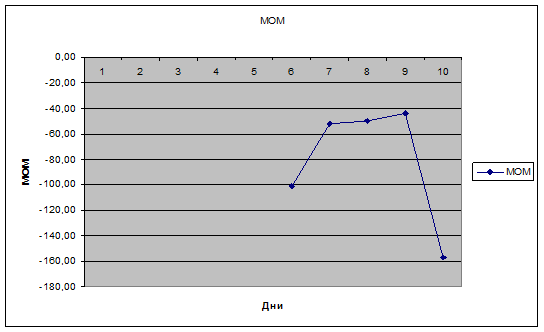
Рисунок 3: График момента.
Скорость изменения цен
(ROCt). Это
похожий на МОМ индикатор, который расчитывается как отношение конечной цены
текущего дня к цене n дней тому назад: 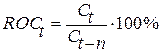 .
.
где C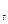 - цена
закрытия t-го дня;
- цена
закрытия t-го дня;
ROC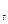 - значение ROC текущего дня t.
- значение ROC текущего дня t.
Таким образом, ROC является отражением скорости изменения цены,
а также указывает направление этого изменения. Правила работы ничем не отличаются
от МОМ, но вместо нулевой линии для принятия решения о купле или продаже
используется уровень 100%. При пересечении этого уровня снизу вверх надо
покупать, а при пересечении сверху вниз – продавать финансовый инструмент.
ROC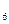 =
=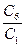 ´100%=
´100%=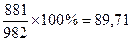
ROC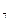 =
=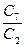 ´100%=
´100%=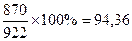
ROC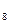 =
=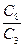 ´100%=
´100%=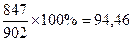
ROC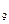 =
=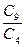 ´100%=
´100%=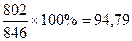
ROC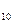 =
= ´100%=
´100%=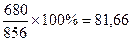
Результаты расчетов скорости изменения цены представлены ниже в таблице
7. График скорости изменения цены представлен на рисунке 4.
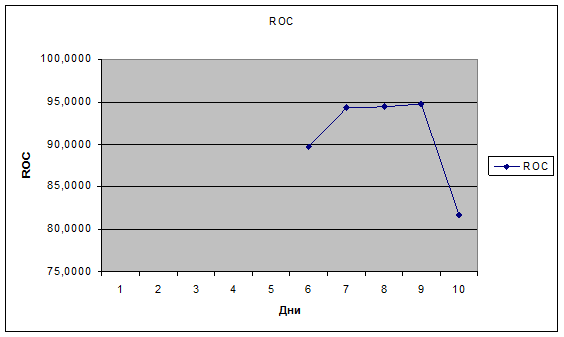
Рисунок 4: График скорости изменения цен.
Значение ROC <100%
свидетельствует  об относительном снижение цен.
об относительном снижение цен.
График ROC движется вверх на протяжение 5-8 дней, на 9 день наблюдается
понижение.
Индекс относительной силы (RSI). Для его расчета применяют следующую формулу:
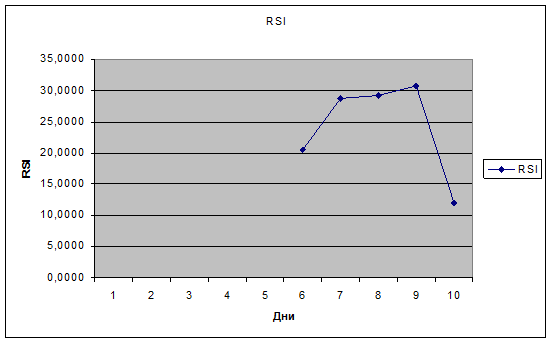
Рисунок 5: график индекса относительной силы.
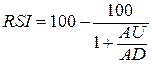
где AU – сумма приростов конечных цен за n дней
AD – сумма убыли конечных цен
за n дней.
Значения
RSI изменяются от 0 до
100. Этот индикатор может подавать сигналы либо одновременно с разворотом цен,
либо с опережением, что является неоценимым достоинством данного индикатора.
Если значения RSI находятся в пределах от 80 до 100 (так
называемая «зона перекупленности»), значит цены сильно выросли, надо ждать их
падения и подготовиться к продаже. Сигналом к продаже служит момент выхода
графика RSI из зоны перекупленности.
Если значения RSI находятся в пределах от 0 до 20 (так
называемая «зона перепроданности»), значит цены упали
слишком низко, надо ждать их роста и подготовиться к покупке. Сигналом к
покупке служит момент выхода графика RSI
из зоны перепроданности.
Расхождение между
направлением движения цен и осциллятора (дивергенция) указывает на близость
разворота тренда. Особенно серьезным этот сигнал является, когда осциллятор
находится в критической области (перекупленности или перепроданности).
RSI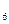 =100-100/(1+35/136)=20,47
=100-100/(1+35/136)=20,47
RSI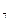 = 100-100/(1+35/87)=28,69
= 100-100/(1+35/87)=28,69
RSI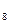 = 100-100/(1+35/75)=29,17
= 100-100/(1+35/75)=29,17
RSI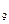 = 100-100/(1+35/79)=30,70
= 100-100/(1+35/79)=30,70
RSI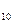 = 100-100/(1+25/182)=12,08
= 100-100/(1+25/182)=12,08
По графику RSI мы
видим, что начиная с 6-го дня значения выходят из «зоны перепроданности», что
служит сигналом к покупке. На 9-ый день значения RSI снова уходят в «зону
перепроданности», значит цены упали слишком низко.
Стохастические
линии (%К, %R и %D).
Стохастические линии строятся не только на основании цен закрытия но и с использованием максимальной и минимальной
цены.
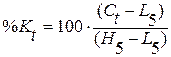 ;
; 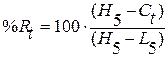 ;
; 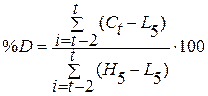
где Ct - цена закрытия;
L5 – значение минимальной цены за
5 предшествующих дней;
H5 – значение максимальной цены за 5 предшествующих дней.
Смысл индексов %К и %R
состоит в том, что при росте цен цена закрытия бывает ближе к максимальной, а
при падении цен наоборот – ближе к минимальной. Индексы %К и %R
проверяют куда больше тяготеет цена закрытия.
%К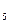 = 100´(856-823)/(998-823)=18,86
= 100´(856-823)/(998-823)=18,86
%К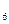 = 100´(881-823)/(970- 823)=39,46
= 100´(881-823)/(970- 823)=39,46
%К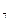 = 100´(870-823)/(950-823)=37,00
= 100´(870-823)/(950-823)=37,00
%К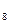 = 100´(852-823)/(930- 823)=27,10
= 100´(852-823)/(930- 823)=27,10
%К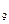 = 100´(802-800)/(930-800)=1,54
= 100´(802-800)/(930-800)=1,54
%К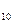 = 100´(699-680)/(930-6880)=7,60
= 100´(699-680)/(930-6880)=7,60
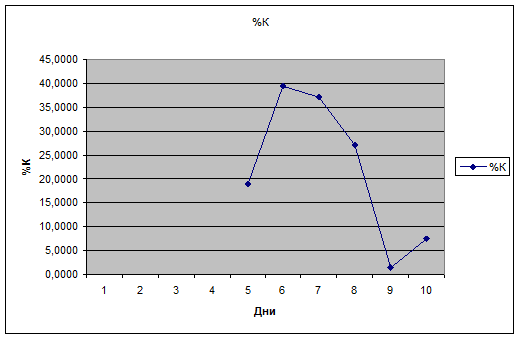
Цена закрытия тяготеет к росту.
Похожая формула используется для расчета %R:
%R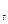 = 100´( H
= 100´( H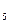 - С
- С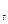 )/( H
)/( H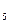 - L
- L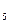 ),
),
где %R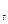 - значение
индекса текущего дня t; С
- значение
индекса текущего дня t; С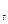 - цена закрытия текущего дня t; L
- цена закрытия текущего дня t; L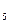 и H
и H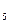 - минимальная
и максимальная цены за n
предшествующих дней, включая текущий.
- минимальная
и максимальная цены за n
предшествующих дней, включая текущий.
Смысл индексов %К и %R состоит в том, что при росте цен цена закрытия
бывает ближе к максимальной цене, а при падении цен, наоборот, ближе к минимальной.
Индексы %К и %R
проверяют, куда больше тяготеет цена закрытия. При расчете %К разность между
ценой закрытия текущего дня и минимальной ценой за 5 дней сравнивают с размахом
цен за эти же 5 дней. В случае расчета %R с размахом сравнивают разность между
максимальной ценой за 5 дней и ценой закрытия.
%R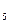 = 100´(998-856)/( 998-823)=81,14
= 100´(998-856)/( 998-823)=81,14
%R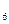 = 100´(970-881)/(970-823)=60,54
= 100´(970-881)/(970-823)=60,54
%R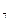 = 100´(950-870)/(950-823)=62,99
= 100´(950-870)/(950-823)=62,99
%R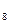 = 100´(930-852)/(930-823)=72,89
= 100´(930-852)/(930-823)=72,89
%R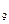 = 100´(930-802)/(930-800)=98,46
= 100´(930-802)/(930-800)=98,46
%R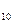 = 100´(930-699)/(930-680)=92,40
= 100´(930-699)/(930-680)=92,40
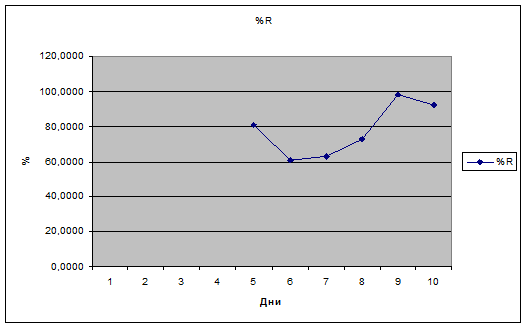
Цена закрытия тяготеет к росту.
Индекс %D рассчитывается аналогично индексу %К, с той
лишь разницей, что при его построении величины (С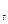 -L
-L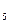 ) и (H
) и (H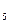 -C
-C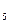 ) сглаживают,
беря их трехдневную сумму.
) сглаживают,
беря их трехдневную сумму.
%D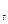 =
=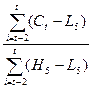 ´100,
´100,
смысл входящих в формулу величин был пояснен
ранее.
%D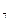 =
=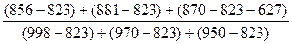 ´100=30,74
´100=30,74
%D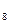 =
=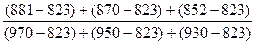 ´100=35,17
´100=35,17
%D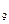 =
=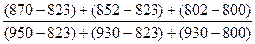 ´100=21,43
´100=21,43
%D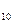 =
=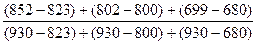 ´100=10,27
´100=10,27
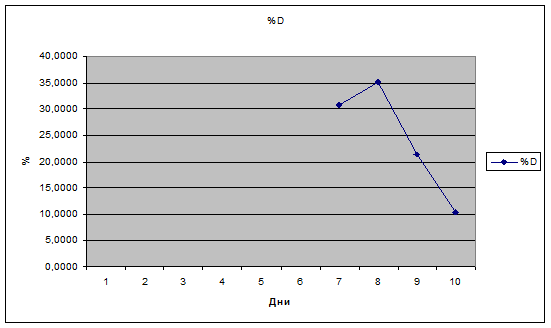
Цена закрытия тяготеет к повышению.
|
Дни t
|
Максимальная цена за день
|
Минимальная цена за день
|
Цена закрытия
|
Экспоненциальная скользящая средняя
|
МОМ
|
RОС
|
Повышение цены
|
Пониже-ние цены
|
Сумма повышений
|
Сумма понижений
|
RSI
|
Максимальная цена за 5 дней
|
Минимальная цена за 5 дней
|
%R
|
%K
|
%D
|
|
1
|
998
|
970
|
982
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
970
|
922
|
922
|
|
|
|
|
60
|
|
|
|
|
|
|
|
|
|
3
|
950
|
884
|
902
|
|
|
|
|
20
|
|
|
|
|
|
|
|
|
|
4
|
880
|
823
|
846
|
|
|
|
|
56
|
|
|
|
|
|
|
|
|
|
5
|
920
|
842
|
856
|
901,6000
|
|
|
10
|
|
|
|
|
998
|
823
|
81,1429
|
18,8571
|
|
|
6
|
889
|
840
|
881
|
894,7333
|
-101
|
89,7149
|
25
|
|
35
|
136
|
20,4678
|
970
|
823
|
60,5442
|
39,4558
|
|
|
7
|
930
|
865
|
870
|
886,4889
|
-52
|
94,3601
|
|
11
|
35
|
87
|
28,6885
|
950
|
823
|
62,9921
|
37,0079
|
30,7350
|
|
8
|
890
|
847
|
852
|
874,9926
|
-50
|
94,4568
|
|
18
|
35
|
85
|
29,1667
|
930
|
823
|
72,8972
|
27,1028
|
35,1706
|
|
9
|
866
|
800
|
802
|
850,6617
|
-44
|
94,7991
|
|
50
|
35
|
79
|
30,7018
|
930
|
800
|
98,4615
|
1,5385
|
21,4286
|
|
10
|
815
|
680
|
699
|
800,1078
|
-157
|
81,6589
|
|
103
|
25
|
182
|
12,0773
|
930
|
680
|
92,4000
|
7,6000
|
10,2669
|
Задача № 3.
Выполнять
различные коммерческие расходы, используя данные, приведенные в таблице. В
условии задачи значения параметров приведены в виде переменных. Например, S означает некую сумму
средств в рублях, Тлет – время в годах, i – ставку в процентах и т.д. По
именам переменных из таблицы необходимо выбрать соответствующие численные
значения параметров и выполнить расчеты.
|
Сумма
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
Ставка
|
Число начислений
|
|
S
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
500000
|
21.01.2002
|
11.03.2002
|
180
|
4
|
10
|
2
|
1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды –
Тн, возврата – Тк. День выдачи и день возврата считать за один день. Проценты
рассчитываются по простой процентной ставке i% годовых. Найти:
1.1.
точные проценты с точным числом дней ссуды;
1.2.
обыкновенные проценты с точным числом дней ссуды;
1.3.
обыкновенные проценты с приближенным числом дней ссуды.
2.
Через Тдн дней после подписания договора
должник уплатит S руб.
Кредит выдан под i%
годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
3.
Через Тдн дней предприятие должно получить
по векселю S рублей.
Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год равен
360 дней).
4.
В кредитном договоре на сумму S рублей и сроком на Тлет
лет, зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную
сумму.
5.
Ссуда, размером S рублей предоставлена на Тлет.
Проценты сложные, ставка – i%
годовых. Проценты начисляются m
раз в году. Вычислить наращенную сумму.
6.
Вычислить эффективную ставку процента, если банк
начисляет проценты m
раз в году, исходя из номинальной ставки i%
годовых.
7.
Определить, какой должна быть номинальная ставка при
начислении процентов m
раз в году, чтобы обеспечить эффективную ставку i% годовых.
8.
Через Тлет предприятию будет выплачена сумма
S рублей. Определить ее
современную стоимость при условии, что применяется сложная процентная ставка i% годовых.
9.
Через Тлет по векселю должна быть выплачена
сумма S рублей. Банк
учел вексель по сложной учетной ставке i% годовых. Определить
дисконт.
10.
В течение Тлет лет на расчетный счет в конце
каждого года поступает по S
рублей, которые m раз в
году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном
счете к концу указанного срока.
Решение.
1.1.
Рассчитаем точные проценты с точным числом дней ссуды
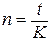
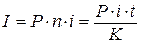 ,
,
где n - срок ссуды;
K – число дней в году;
i – процентная ставка;
t – срок операции (ссуды) в днях;
Р – размер
ссуды;
К = 365, t = 49 (с 21.01.2002 по
11.03.2002)
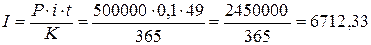
1.2.
Рассчитаем обыкновенные проценты с точным числом дней ссуды
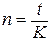
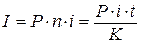 ,
,
где n - срок ссуды;
K – число дней в году;
i – процентная ставка;
t – срок операции (ссуды) в днях;
Р – размер
ссуды;
К = 360, t = 49 (с 21.01.2002 по
11.03.2002)
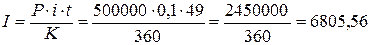
1.3. Рассчитаем обыкновенные проценты с приближенным числом
дней ссуды
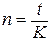
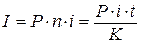 ,
,
где n - срок ссуды;
K – число дней в году;
i – процентная ставка;
t – срок операции (ссуды) в днях;
Р – размер
ссуды;
К = 360, t = 50
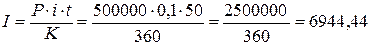
2. Рассчитаем первоначальную
сумму по формуле: 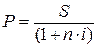
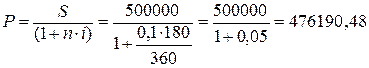 руб.
руб.
Найдем дисконт: 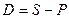
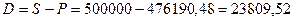
3. Определим
полученный предприятием дисконт по формуле: 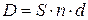
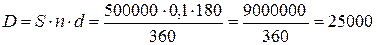 руб.
руб.
Сумма, полученная
предприятием, равна: 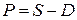
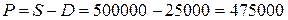 руб.
руб.
4. Определим
наращенную сумму по формуле:
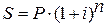
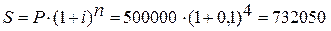 руб.
руб.
5. Рассчитаем наращенную сумму: 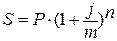
Всего начислений за 4 года:
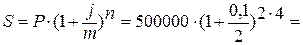 738727,72 руб
738727,72 руб
6. Вычислим эффективную ставку
процента: 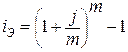
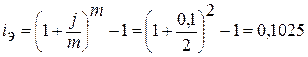 , т.е. 10,25%.
, т.е. 10,25%.
7. Определим
номинальную ставку процента.
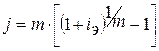
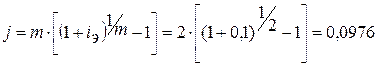 , т.е. 9,76%.
, т.е. 9,76%.
8. Найдем
современную стоимость.
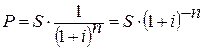
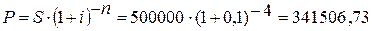
9. Рассчитаем
дисконт.
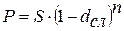
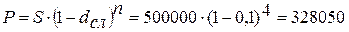 руб.
руб.
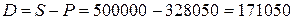
10. Определим
сумму на расчетном счете к концу 5 лет.
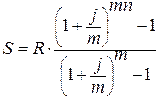
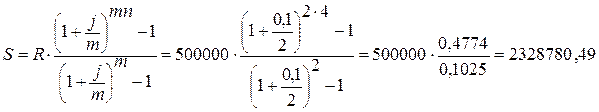 руб.
руб.