Задание 1
Стоимостной
МОБ включает пять отраслей:
1.
тяжелая промышленность;
2.
легкая промышленность;
3.
строительство;
4.
сельское и лесное хозяйство;
5.
прочие отрасли.
1) Необходимо
составить плановый МОБ, если спрос на конечную продукцию на следующий год по
всем отраслям увеличится на (4+n)%.
2) Проследить
эффект распространения, вызванный увеличением спроса на продукцию тяжелой
промышленности дополнительно на (2+n/2)%.
3) Определить
равновесные цены в предположении (4+n/3)%-го
роста заработной платы по каждой отрасли. Проследите эффект распространения,
вызванный дополнительным ростом заработной платы в легкой промышленности на 5%
(считайте, что доли заработной платы в добавленной стоимости по отраслям
соответственно равны 0,5, 0,517, 0,499, 0,345, 0,547).
Таблица 1
Таблица межотраслевых потоков
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
46,07
|
3,28
|
17,64
|
6,19
|
4,82
|
|
2
|
3,92
|
38,42
|
0,84
|
0,86
|
2,25
|
|
3
|
0
|
0
|
0
|
0
|
0
|
|
4
|
0,52
|
27,22
|
1,01
|
16,18
|
0
|
|
5
|
16,08
|
10,1
|
4,73
|
0,34
|
0,4
|
Таблица 2
Таблица конечных продуктов
|
1
|
41,76
|
|
2
|
79,02
|
|
3
|
37,96
|
|
4
|
24,25
|
|
5
|
2,64
|
Таблица 3
Таблицы стоимости фондов и
затрат труда
|
Стоимость
фондов
|
100
|
110
|
80
|
150
|
60
|
|
Стоимость
затрат труда
|
90
|
100
|
85
|
62
|
45
|
Решение:
Введем следующие обозначения:
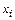 – общий (валовой) объем продукции i-ой отрасли;
– общий (валовой) объем продукции i-ой отрасли;
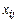 – объем продукции i-ой отрасли, потребляемой j-ой отраслью (i, j = 1, 2, ... п);
– объем продукции i-ой отрасли, потребляемой j-ой отраслью (i, j = 1, 2, ... п);
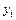 – объем конечного продукта i-ой отрасли
для непроизводственного потребления.
– объем конечного продукта i-ой отрасли
для непроизводственного потребления.
Общий вид межотраслевого баланса представлен в таблице.
Она состоит из четырех разделов. Первый раздел образуется перечнем
"чистых" отраслей. Каждая отрасль представлена в МОБ дважды: как
производящая и как потребляющая. Отрасли как производителю
соответствует строка таблицы, отрасли как потребителю соответствует столбец.
На пересечении i-й строки и j-го
столбца находится величина xij - количество продукции
i-й отрасли (в денежном выражении), израсходованной на производственные
нужды j-й отрасли. Таким образом, первый раздел характеризует межотраслевые
потоки сырья, материалов, энергии и т. д., обусловленные производственной
деятельностью отраслей.
|
|
1
|
2
|
…
|
n
|
У
|
Х
|
|
1
|
x11
|
x12
|
…
|
x1n
|
y1
|
x1
|
|
2
|
х21
|
x22
|
|
x2n
|
y2
|
x2
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
n
|
xn1
|
xn2
|
…
|
xnn
|
yn
|
xn
|
|
Z
|
z 1
|
z2
|
…
|
zn
|
|
|
|
Х
|
x1
|
x2
|
. . .
|
xn
|
|
|
Второй
раздел МОБ состоит из двух столбцов. Столбец
Y - это конечная продукция отраслей. Конечная продукция включает
в себя непроизводственное потребление (личное и общественное), возмещение
выбытия основных фондов и накопление. Столбец Х содержит величины валового
производства отраслей.
Третий
раздел представлен двумя нижними строками. Строка Х содержит те же
самые величины, что и соответствующий столбец второго раздела. Строка V
содержит величины условно-чистой продукции отраслей. Условно-чистая
продукция включает в себя амортизационные отчисления и вновь созданную
стоимость (заработную плату и прибыль).
Четвертый
раздел МОБ не имеет непосредственного отношения к анализу межотраслевых
связей. Он характеризует перераспределительные отношения в народном хозяйстве
и здесь рассматриваться не будет.
Строки показывают
распределение продукции. Для любой i-й строки первого раздела справедливо
соотношение
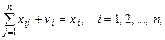
т.е. вся произведенная i-й отраслью продукция хi (валовая продукция в денежном
выражении) делится на промежуточную и конечную. Промежуточная продукция - это
та часть валовой продукции i-й отрасли, которая расходуется другими отраслями в
процессе осуществления ими собственных производственных функций.
Столбцы МОБ показывают
структуру затрат. Для любого j-го столбца можно записать:

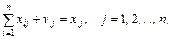
т.е. стоимость всей произведенной
j-й отраслью
продукции хj состоит из текущих производственных
затрат и условно-чистой продукции vj.
Суммарный конечный
продукт равен суммарной условно-чистой продукции. Действительно,
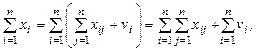
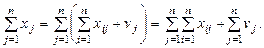
Сравнивая
правые части этих соотношений, видим, что

Зная суммарный конечный
продукт или, что то же, суммарную условно-чистую продукцию, можно определить национальный
доход. Он равен разности суммарного конечного продукта и амортизационных
отчислений, направляемых на возмещение выбытия основных фондов.
Так как 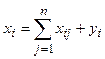 . Перепишем эту систему уравнений
. Перепишем эту систему уравнений 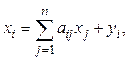 введя коэффициенты
прямых затрат
введя коэффициенты
прямых затрат 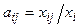 . Обозначим Х – вектор валового выпуска, Y – вектор конечного продута, А = (аij) – матрица прямых затрат, (i, j = 1, 2, ... п). Тогда соотношения баланса перепишутся в матричном виде:
. Обозначим Х – вектор валового выпуска, Y – вектор конечного продута, А = (аij) – матрица прямых затрат, (i, j = 1, 2, ... п). Тогда соотношения баланса перепишутся в матричном виде: 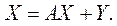 Это соотношение
называется матричным уравнением
Леонтьева.
Это соотношение
называется матричным уравнением
Леонтьева.
Основная задача
межотраслевого баланса состоит в отыскании таково вектора валового выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y. Перепишем
последнее уравнение в виде 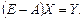
Если 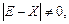 то решение задачи
межотраслевого баланса записывается
то решение задачи
межотраслевого баланса записывается 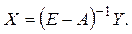
Матрица  называется матрицей
полных затрат.
называется матрицей
полных затрат.
Представим исходные данные задачи в виде одной таблицы –
матрицы межотраслевого баланса:
|
|
ОТРАСЛЬ
|
1
|
2
|
3
|
4
|
5
|
Конечный продукт
|
Валовой продукт
|
|
1
|
тяжелая промышленность
|
46,07
|
3,28
|
17,64
|
6,19
|
4,82
|
41,76
|
126,18
|
|
2
|
легкая промышленность
|
3,92
|
38,42
|
0,84
|
0,86
|
2,25
|
79,02
|
137,45
|
|
3
|
строительство
|
0
|
0
|
0
|
0
|
0
|
37,96
|
43,8
|
|
4
|
сельское и лесное хозяйство
|
0,52
|
27,22
|
1,01
|
16,18
|
0
|
24,25
|
73,26
|
|
5
|
прочие отрасли
|
16,08
|
10,1
|
4,73
|
0,34
|
0,4
|
2,64
|
34,69
|
|
|
Условно-чистый продукт 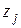
|
59,59
|
58,43
|
19,58
|
49,69
|
27,22
|
|
|
|
|
Валовый продукт 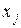
|
126,18
|
137,45
|
43,8
|
73,26
|
34,69
|
|
|
При составлении таблицы
рассчитали величину условно-чистой продукции. Так, для первой отрасли эта
величина:
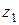 = 126,18 – 46,07 –3,92
– 0,52 – 16,08 = 59,59.
= 126,18 – 46,07 –3,92
– 0,52 – 16,08 = 59,59.
И так для каждой отрасли
1) Матричные
вычисления произведем с помощью пакета Excel. Итак, матрицы 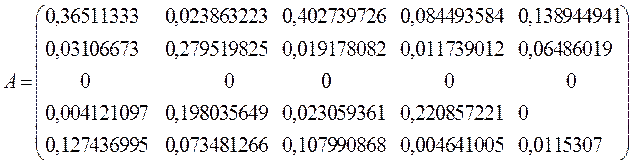
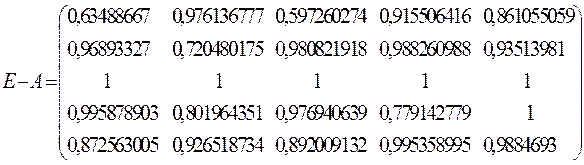 .
.
Матрица полных затрат
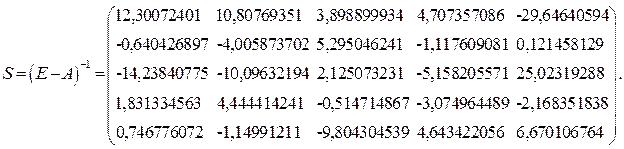
По условию задачи, спрос
по всем отраслям должен увеличиться на 8%, т.е. вектор конечного продукта
должен стать 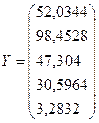 .
.
Тогда искомый вектор
валового выпуска
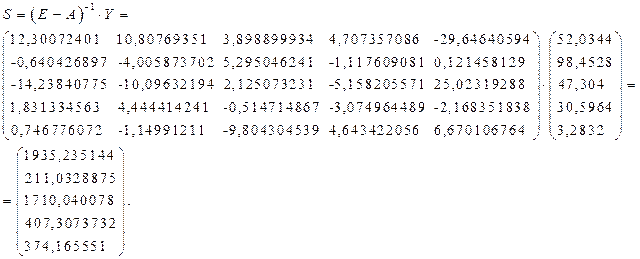
Составим новую матрицу межотраслевого
баланса (с точностью до второго знака после запятой). Для этого воспользуемся формулами:
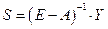 ;
;
 ;
;
 ;
;
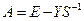 .
.
Промежуточные вычисления
(с точностью до 2-го знака после запятой:
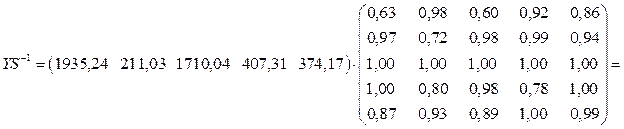
=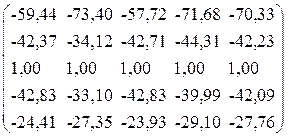 .
.
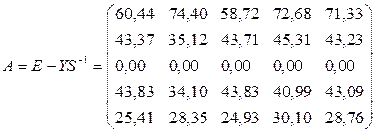
После чего
новая матрица межотраслевого баланса будет выглядеть:
|
|
ОТРАСЛЬ
|
1
|
2
|
3
|
4
|
5
|
Конечный продукт
|
Валовой продукт
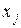
|
|
1
|
тяжелая промышленность
|
60,438
|
74,404
|
58,72
|
72,679
|
71,33
|
3875,28
|
4212,85
|
|
2
|
легкая промышленность
|
43,375
|
35,122
|
43,712
|
45,307
|
43,227
|
4424,46
|
4635,2
|
|
3
|
строительство
|
0
|
0
|
0
|
0
|
0
|
3804,54
|
3804,54
|
|
4
|
сельское и лесное хозяйство
|
43,828
|
34,105
|
43,825
|
40,993
|
43,092
|
4380,10
|
4585,94
|
|
5
|
прочие отрасли
|
25,413
|
28,346
|
24,929
|
30,096
|
28,756
|
4350,89
|
4488,43
|
|
|
Условно-чистый продукт 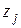
|
4039,796
|
4463,223
|
3633,354
|
4396,865
|
4302,025
|
|
|
|
|
Валовый продукт 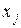
|
4212,85
|
4635,2
|
3804,54
|
4585,94
|
4488,43
|
|
|
2) Проследить
эффект распространения, вызванный увеличением спроса на продукцию тяжелой
промышленности дополнительно на 6%, т.е.
конечный продукт станет равным
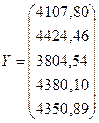 .
.
В результате этого
изменения эффект распространения будет заключаться в том, что новый вектор валового
выпуска будет иметь вид
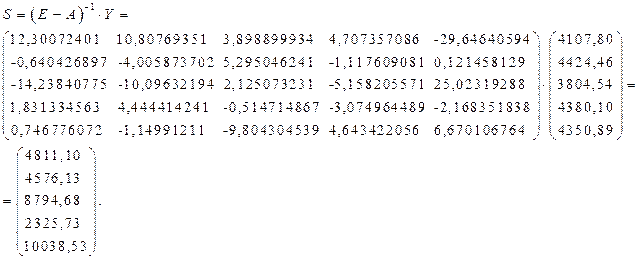
Для нахождения эффекта
распространения привлечем уравнение для цен:
P
= AT P + v, откуда P = (E – AT)-1v.
Обратная
матрица Леонтьева (E – AT)-1 – ценовой матричный
мультипликатор – матричный мультипликатор ценового эффекта распространения.
Этот мультипликатор
эффекта распространения найдем с помощью пакета Excel, сначала транспонируя матрицу А,
затем отнимая ее от единичной матрицы и находя обратную матрицу. Проводя эти
вычисления, получим:
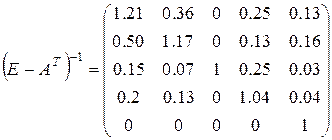 .
.
Этот результат в качестве
промежуточного будет использован в следующем пункте при расчете равновесной
цены.
3) Отношение
vj = Vj/Xj – называют долей добавленной
стоимости, а вектор v = (v1,…,vn) – вектор долей добавленной
стоимости.
По
условию задачи, вектор v = (0,5, 0,517, 0,499, 0,345,
0,547), тогда
Vj = vj ∙ Xj. Для каждого значения индекса получаем:
V1 = v1 ∙ X1 = 0,5 ∙ 4212,85 = 2106,425.
И так для остальных значений индекса.
Тогда V = (2106,425; 2396,398; 1898,465;
1582,149; 2455,171)
В матричном виде
уравнение для цен будет иметь следующий вид
P = AT P + v.
Решая уравнение это
относительно Р, получим
P = (E – AT)-1v.
По условию
задачи, вектор v = (0,5, 0,517, 0,499, 0,345,
0,547).
Тогда, с
помощью пакета Excel, найдем
равновесные цены:
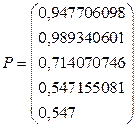 .
.
При
этом эффект распространения, вызванный дополнительным ростом заработной платы в
легкой промышленности на 5% (считая, что доли заработной платы в добавленной
стоимости по отраслям соответственно равны 0,5, 0,517, 0,499, 0,345, 0,547)
дается мультипликатором эффекта распространения:
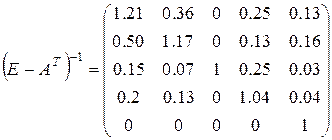 .
.
Задание 2
Условие
задания:
Имеются
данные экономического развития США за 1953-1974 гг.
|
Год
|
Валовой национальный продукт, млрд.
долл.
|
Объем загруженного капитала, млрд.
долл
|
Количество отработанных часов,
млрд. час.
|
|
1953
|
623,6
|
380,53
|
136,07
|
|
1954
|
616,1
|
354,20
|
131,12
|
|
1955
|
657,5
|
400,66
|
134,16
|
|
1956
|
671,6
|
415,15
|
136,04
|
|
1957
|
683,8
|
418,83
|
134,77
|
|
1958
|
680,9
|
384,87
|
130,44
|
|
1959
|
721,7
|
431,04
|
133,87
|
|
1960
|
737,2
|
435,65
|
134,99
|
|
1961
|
756,6
|
432,28
|
134,25
|
|
1962
|
800,3
|
471,65
|
137,36
|
|
1963
|
832,5
|
499,75
|
138,72
|
|
1964
|
876,4
|
535,09
|
141,00
|
|
1965
|
926,3
|
593,96
|
145,39
|
|
1966
|
984,4
|
644,26
|
150,88
|
|
1967
|
1011,4
|
647,58
|
152,67
|
|
1968
|
1058,1
|
628,43
|
155,51
|
|
1969
|
1087,6
|
711,58
|
159,20
|
|
1970
|
1085,6
|
628,06
|
156,49
|
|
1971
|
1122,4
|
696,74
|
155,85
|
|
1972
|
1185,9
|
770,96
|
159,56
|
|
1973
|
1255,0
|
850,63
|
165,41
|
|
1974
|
1248,0
|
848,39
|
165,51
|
Необходимо
определить:
1.
Параметры А, a и b степенной
производственной функции;
2.
Расчетные значения ВНП;
3.
Оценить точность полученной модели;
4.
Эластичность выпуска и производства;
5.
Для 1974 года построить изокванту и изоклинали.
Решение:
1. Определение параметров А, a и b степенной производственной функции проведем с
помощью пакета Excel. Будем
искать параметры производственной функции в виде 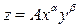 ,
где
,
где 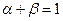 , причем a и b положительные.
, причем a и b положительные.
Для
определения параметров модели сведем задачу к нахождению параметров линейной
корреляционной модели, прологарифмировав обе части равенства 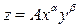 :
:
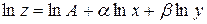 .
.
Далее
уменьшим количество неизвестных, учтя, что 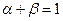 :
:
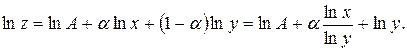
Таким
образом, задача свелась к нахождению коэффициентов линейной корреляционной
модели:
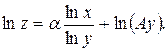
Для
удобства введем обозначения:
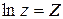 ;
; 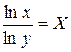 ;
; 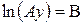 . Тогда модель будет выглядеть:
. Тогда модель будет выглядеть:
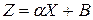 .
.
Для отыскания значений параметров а и Ь, при которых f(a,b) принимает минимальное значение,
частные производные функции приравниваем нулю и преобразуем получаемые
уравнения, которые называются нормальными
уравнениями МНК для прямой:

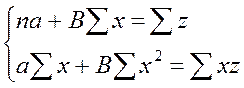
Нормальные уравнения МНК для прямой
линии регрессии являются системой двух уравнений с двумя неизвестными a и
B. Все остальные
величины, входящие в систему, определяются по расчетной информации из следующей
таблицы.
Используя
пакет Эксель, составим вспомогательную таблицу с применением соответствующего
логарифмирования для вычисления коэффициентов этой модели:
|
Год
|
Z
|
X
|
Z*X
|
Z*Z
|
X*X
|
|
1953
|
6,44
|
5,94
|
38,24
|
41,42
|
35,30
|
|
1954
|
6,42
|
5,87
|
37,70
|
41,26
|
34,46
|
|
1955
|
6,49
|
5,99
|
38,89
|
42,10
|
35,92
|
|
1956
|
6,51
|
6,03
|
39,24
|
42,38
|
36,34
|
|
1957
|
6,53
|
6,04
|
39,41
|
42,61
|
36,45
|
|
1958
|
6,52
|
5,95
|
38,83
|
42,55
|
35,44
|
|
1959
|
6,58
|
6,07
|
39,93
|
43,32
|
36,80
|
|
1960
|
6,60
|
6,08
|
40,12
|
43,60
|
36,93
|
|
1961
|
6,63
|
6,07
|
40,23
|
43,94
|
36,83
|
|
1962
|
6,68
|
6,16
|
41,15
|
44,69
|
37,90
|
|
1963
|
6,72
|
6,21
|
41,79
|
45,22
|
38,62
|
|
1964
|
6,78
|
6,28
|
42,57
|
45,91
|
39,47
|
|
1965
|
6,83
|
6,39
|
43,63
|
46,67
|
40,79
|
|
1966
|
6,89
|
6,47
|
44,58
|
47,50
|
41,84
|
|
1967
|
6,92
|
6,47
|
44,79
|
47,87
|
41,90
|
|
1968
|
6,96
|
6,44
|
44,87
|
48,50
|
41,52
|
|
1969
|
6,99
|
6,57
|
45,92
|
48,88
|
43,13
|
|
1970
|
6,99
|
6,44
|
45,03
|
48,86
|
41,51
|
|
1971
|
7,02
|
6,55
|
45,98
|
49,33
|
42,86
|
|
1972
|
7,08
|
6,65
|
47,05
|
50,10
|
44,19
|
|
1973
|
7,13
|
6,75
|
48,13
|
50,91
|
45,51
|
|
1974
|
7,13
|
6,74
|
48,08
|
50,83
|
45,47
|
|
сумма
|
148,86
|
138,15
|
936,16
|
1008,44
|
869,16
|
|
среднее
|
6,77
|
6,28
|
42,55
|
45,84
|
39,51
|
Параметр b вычисляется по преобразованной формуле, которую можно
вывести, решая систему нормальных уравнений относительно b:
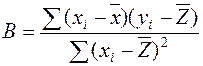
Подставим полученные значения из таблицы 3 в формулу и рассчитаем a и b:
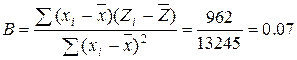
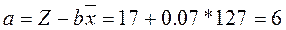
Искомая зависимость выглядит следующим образом:
Z = 6 + 0,07х.
Итак, a =
0.07; 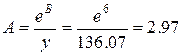 .
.
Тогда искомый вид производственной функции:
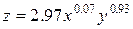 .
.
2.
С помощью пакета Excel найдем
расчетные значения ВНП:
|
Год
|
Валовой национальный продукт, млрд. долл.
|
Объем загруженного капитала, млрд. долл
|
Количество отработанных часов, млрд. час.
|
Расчет ВНП
|
отклонение расчета от факта
|
|
1953
|
623,6
|
380,53
|
136,07
|
597,4321
|
26,168
|
|
1954
|
616,1
|
354,2
|
131,12
|
556,094
|
60,006
|
|
1955
|
657,5
|
400,66
|
134,16
|
629,0362
|
28,464
|
|
1956
|
671,6
|
415,15
|
136,04
|
651,7855
|
19,815
|
|
1957
|
683,8
|
418,83
|
134,77
|
657,5631
|
26,237
|
|
1958
|
680,9
|
384,87
|
130,44
|
604,2459
|
76,654
|
|
1959
|
721,7
|
431,04
|
133,87
|
676,7328
|
44,967
|
|
1960
|
737,2
|
435,65
|
134,99
|
683,9705
|
53,23
|
|
1961
|
756,6
|
432,28
|
134,25
|
678,6796
|
77,92
|
|
1962
|
800,3
|
471,65
|
137,36
|
740,4905
|
59,81
|
|
1963
|
832,5
|
499,75
|
138,72
|
784,6075
|
47,892
|
|
1964
|
876,4
|
535,09
|
141
|
840,0913
|
36,309
|
|
1965
|
926,3
|
593,96
|
145,39
|
932,5172
|
-6,217
|
|
1966
|
984,4
|
644,26
|
150,88
|
1011,4882
|
-27,09
|
|
1967
|
1011,4
|
647,58
|
152,67
|
1016,7006
|
-5,301
|
|
1968
|
1058,1
|
628,43
|
155,51
|
986,6351
|
71,465
|
|
1969
|
1087,6
|
711,58
|
159,2
|
1117,1806
|
-29,58
|
|
1970
|
1085,6
|
628,06
|
156,49
|
986,0542
|
99,546
|
|
1971
|
1122,4
|
696,74
|
155,85
|
1093,8818
|
28,518
|
|
1972
|
1185,9
|
770,96
|
159,56
|
1210,4072
|
-24,51
|
|
1973
|
1255
|
850,63
|
165,41
|
1335,4891
|
-80,49
|
|
1974
|
1248
|
848,39
|
165,51
|
1331,9723
|
-83,97
|
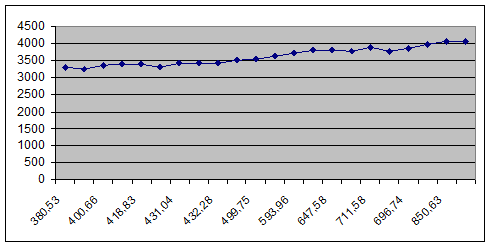
3. Оценим точность
полученной модели, для этого выполним графическое представление результатов
вычислений.
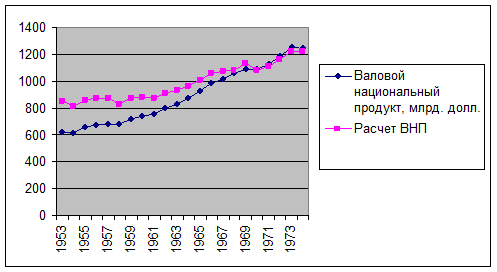
Как можно видеть из
табличных значений и графического представления, расчетные значения, по крайней
мере, повторяют тенденцию фактических значений с ошибкой порядка ±7%.
4. Оценим эластичность
производственной функции по объему загруженного капитала и количеству отработанных часов, т.е.
эластичность функции z по переменной х
и эластичность функции z по переменной у.
В общем виде эластичность
степенной производственной функции от двух переменных будет выглядеть следующим
образом:
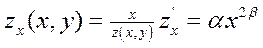 ;
;
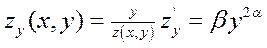 .
.
Для рассматриваемой
функции:
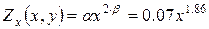 .
.
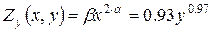 .
.
Таким образом, ВНП
пропорционален коэффициентам a и b, но не коэффициенту А.
5. Для 1974 года построим
изокванту и изоклинали.
Графическое изображение
функции представлено изоквантой. Она подобна кривой безразличия, только
отличие состоит в том, что изокванта количественно определена. Объем выпуска,
соответствующий конкретной изокванте может быть достигнут при различном
сочетании капитала и труда.
Итак, для 1974 года
уравнение для построения изокванты выглядит:
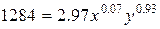
Отсюда
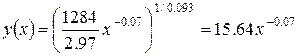 ..
..
Изокванта
выглядит:
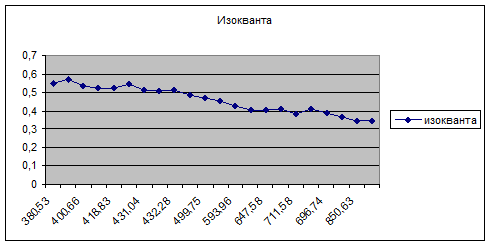
Изоклиналь:
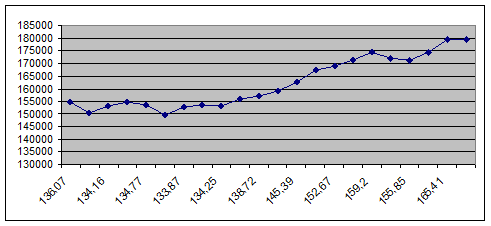
Изоклиналь: