Содержание

Содержание. 2

Введение. 2

Задание. 4

Тема 1: Логические основы системы Пролог-Д. 5

Логические основы работы.. 5

1.1.2. Описать на языке логики первого порядка свойства отношения равенство  5

Тема 2: Построение базы знаний. 5

Факты и правила. 5

2.1.2. Опишите на языке Пролог-Д состав своей семьи. 5

Арифметика и другие второстепенные предикаты в Прологе-Д.. 9

2.2.2. Опишите на языке Пролог-Д вычисление площадей геометрических фигур: трапеции, треугольника, параллелограмма. 9

2.2.3. Опишите вычисление пощади круга и длины окружности. Какова точность вычисления этих величин? Можно ли вычислить радиус круга по длине окружности?. 12

Рекурсия. 14

2.3.2.Написать на языке Пролог-Д базу знаний, описывающую вычисление сумы чисел натурального ряда. 15

2.3.4. Описать вычисление наименьшего общего кратного. 15

Графические возможности системы Пролог-Д.. 17

2.4.2. Используя рекурсивное определение, напишите базу знаний, описывающую многоэтажный дом. 17

Обработка списков. 20

2.5.2. Напишите базу знаний, описывающую обращение списка (первый элемент становиться последним). 20

Заключение. 22

Список литературы.. 23

Введение

Данная работа посвящена экспертным системам - это система искусственного интеллекта (интеллектуальная система), предназначенная для решения плохо формализованных и слабо структурированных задач в определенных проблемных областях, на основе заложенных в ней знаний специалистов-экспертов В рамках работы было рассмотрено проектирование основной части экспертных систем – баз знаний. Для  каждого заданий создавалась база знаний, хранящая определенный набор данных и правил обработки этих данных. Для разработки баз знаний использовался язык программирования Пролог, свое название получивший от сокращения «Программирование логики».

Математической основой Пролога являются исчисления предикатов преимущественно первого порядка, метод резолюции, теория рекурсивных функций. Одно из заданий посвящено именно логическим основам данного языка. В процессе выполнения работы были рассмотрены основные возможности системы Пролог-Д, а именно, возможность арифметических вычислений, создания графических объектов, использования рекурсии, а также возможности работы со структурами данных (на примере обработки списка).

 

Задание

Тема 1: Логические основы системы Пролог-Д.

1.     Логические основы работы.

1.1.2. Опишите на языке логики первого порядка свойство отношения равенства

Тема 2: Построение базы знаний

1.     Факты и правила

2.1.2. Опишите на языке Пролог-Д состав своей семьи.

2.     Арифметика и другие второстепенные предикаты в Прологе-Д

2.2.2. Опишите на языке Пролог-Д вычисление площадей геометрических фигур: трапеции, треугольника, параллелограмма.

2.2.3. Опишите вычисление пощади круга и длины окружности. Какова точность вычисления этих величин? Можно ли вычислить радиус круга по длине окружности?

3.     Рекурсия

2.3.2.Написать на языке Пролог-Д базу знаний, описывающую вычисление сумы чисел натурального ряда.

2.3.4. Описать вычисление наименьшего общего кратного.

4.     Графические возможности системы Пролог-Д

2.4.2. Используя рекурсивное определение, напишите базу знаний, описывающую многоэтажный дом.

5.     Обработка списков

2.5.2. Напишите базу знаний, описывающую обращение списка (первый элемент становиться последним).

Тема 1: Логические основы системы Пролог-Д.

Логические основы работы

1.1.2. Описать на языке логики первого порядка свойства отношения равенство

С помощью языка логики первого порядка можно описать все задачи, решаемые на ЭВМ. На его основе построен и система Пролог-Д.

Отношение равенство запишем как РАВНО(X,Y). Это отношение принимает значение ИСТИНА, если X равен Y, и значение ЛОЖЬ если X и Y не равны между собой. Отношение равенство обладает следующими свойствами:

-     переменная равна сама себе (рефлексивность);

-     если X=Y, то Y=X (симметричность);

-     если X=Z  и Z=Y, то X=Z (транзитивность).

На языке логики первого порядка эти свойства будут записаны в следующем виде:

РАВНО (X,X)

РАВНО(X,Y)<-РАВНО(Y,X)

РАВНО(X,Y)<-РАВНО(X,Z)& РАВНО(Z,Y)

Тема 2: Построение базы знаний

Факты и правила

2.1.2. Опишите на языке Пролог-Д состав своей семьи.

Особенностью языка Пролог-Д, отличающей его от других языков, используемых для работы на ЭВМ, является его применение не только для программирования, но, главным образом, для описания данных и правил их обработки. Построение базы знаний на Пролог-Д означает выявление множества исследуемых объектов и связей между ними, совокупность которых описывает явление или процесс. Это свойство системы Пролог-Д может быть использовано для создания баз данных, словарей, естественно-языковых интерфейсов для существующих систем.

В данной задаче будем описывать семью, родственные отношения которой приведены на рисунке.

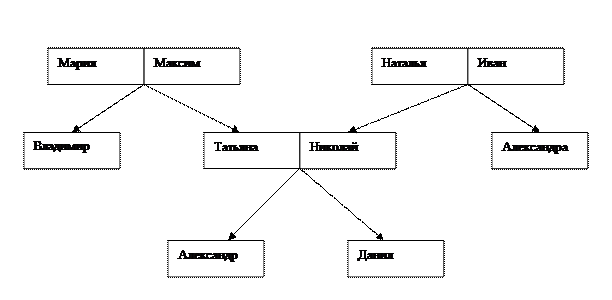
Для записи фактов будут использованы три предиката: родитель(X,Y), женщина (X), мужчина (X). Факт, записанный с помощью предиката родитель (X,Y), имеет место в программе, если X является родителем Y. Факты женщина(X) и мужчина(X) записаны в программе, если их аргументы являются женщиной и мужчиной соответственно.

В задаче о построении родственных отношений могут использоваться правила, описывающие следующие утверждения:

-     X является мамой Y, если X – женщина и X является родителем Y;

-     X является папой Y, если X – мужчина и X является родителем Y;

-     X является дочерью Y, если X – женщина и Н является родителем X;

-     X является сыном Y, если X – мужчина и Н является родителем X;

-     X является бабушкой Y, если X является мамой родителя Y;

-     X является дедушкой Y, если X является папой родителя Y;

-     X является сестрой Y, если X – женщина и  X,Y имеют общую маму;

-     X является братом Y, если  X – мужчина и  X,Y имеют общую маму;

В последних двух правилах учитывается то, что X и Y не являются одним человеком с помощью двух стандартных предикатов РАВНО(Арг1,Арг2) и НЕ(Арг1). Предикат РАВНО имеет два аргумента Арг1 и Арг2. Этот предикат истинен, если успешна унификация Арг1 и Арг2. Аргументом встроенного предиката НЕ является предикат, если этот предикат-аргумент ложен, то предикат НЕ истинный, и наоборот.

 

Программа, реализованная с учетом всех этих утверждений, будет иметь следующий вид:

родитель(Татьяна, Александр);

родитель(Татьяна, Данил);

родитель(Николай, Александр);

родитель(Николай, Данил);

родитель(Мария, Владимир);

родитель(Мария, Татьяна);

родитель(Максим, Владимир);

родитель(Максим, Татьяна);

родитель(Наталья, Николай);

родитель(Наталья, Александра);

родитель(Иван, Николай);

родитель(Иван, Александра);

женщина(Татьяна);

женщина(Мария);

женщина(Наталья);

женщина(Александра);

мужчина(Александр);

мужчина(Данил);

мужчина(Николай);

мужчина(Владимир);

мужчина(Максим);

мужчина(Иван);

мама(X,Y)<-женщина(X),родитель(X,Y);

папа(X,Y)<-мужчина(X),родитель(X,Y);

дочь(X,Y)<-женщина(X),родитель(Y,X);

сын(X,Y)<-мужчина(X),родитель(Y,X);

бабушка(X,Y)<-мама(X,Z),родитель(Z,Y);

дедушка(X,Y)<-папа(X,Z), родитель(Z,Y);

сестра(X,Y)<-женщина(X),мама(Z,X),мама(Z,Y),НЕ(РАВНО(X,Y));

брат(X,Y)<-мужчина(X),мама(Z,X),мама(Z,Y),НЕ(РАВНО(X,Y));

В качестве примера можно привести следующий набор вопросов:

-     найти всех дедушек Александра

-     найти всех бабушек Александра

-     найти маму Александра

-     найти папу Николая

-     найти дочь Максима

-     найти сына Максима

-     найти сестру Николай

-     найти брата Татьяны

?дедушка(H, Александр);

?бабушка(B, Александр);

?мама(M, Александр);

?папа(P, Николай);

?дочь(D, Максим);

?сын(S, Максим);

?сестра(J, Николай);

?брат(G, Татьяна);

Ответ системы Пролог-Д будет

H=Максим

H=Иван

B=Мария

B=Наталья

M=Татьяна

P=Иван

D=Татьяна

S=Владимир

J=Александра

G=Владимир

Арифметика и другие второстепенные предикаты в Прологе-Д

Системы логического программирования, к числу которых относится и язык Пролог-Д,

не предназначены для арифметических вычислений. Традиционные действия, связанные с выполнением арифметических операций, осуществляются посредством использования стандартных предикатом. Данный факт говорит о некотором неудобстве выполнения математических действий в Прологе-Д.

2.2.2. Опишите на языке Пролог-Д вычисление площадей геометрических фигур: трапеции, треугольника, параллелограмма.

Вычисление площади треугольника производиться по формуле 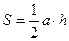, где a – основание треугольника, а h – высота треугольника, проведенная к этому основанию.   Предикат, который выполняется, если найдена площадь треугольника будет иметь имя площадь_треугольника и иметь три аргумента: a – основание треугольника, h – высота треугольник, S – вычисленная площадь. 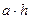При выполнении программы сначала вычисляется произведение  с помощью стандартного предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных между собой соотношением Арг1*Арг2=Арг3. Для вычисления этого произведения стандартный предикат вызывается со  следующим набором аргументов  УМНОЖЕНИЕ(a,h,b), где a – основание треугольника, h – высота проведенная к этому основанию, b – результат выполнения умножения. Далее полученное произведение делится на 2. Для деления используется тот же стандартный предикат, которой вызывается с другими аргументами УМНОЖЕНИЕ(S,2,b), где S – вычисленная площадь треугольника.

Вычисление площади параллелограмма осуществляется по формуле 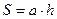, где a – одна из сторон параллелограмма, а h – высота параллелограмма, проведенная к стороне a.   Предикат, который выполняется, если найдена площадь параллелограмма будет иметь имя площадь_параллелограмма и иметь три аргумента: a – сторона параллелограмма, h – его высота, S – вычисленная площадь. Площадь параллелограмма вычисляется с помощью стандартного предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), три аргумента которого связанны соотношением Арг1*Арг2=Арг3.Для этого стандартный предикат вызывается с  следующим набором аргументов  УМНОЖЕНИЕ(a,h,S), где a – основание треугольника, h – высота проведенная к этому основанию, S – результат вычисления площади.

Площадь трапеции вычисляется по формуле 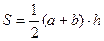, где a, b – основания трапеции, а h –  ее высота. Предикат, который выполняется, если найдена площадь треугольника будет иметь имя площадь_трапеции и иметь четыре аргумента: a, b – основания трапеции, h – высота трапеции, S – вычисленная площадь. Для вычисления площади трапеции используется дополнительный  предикат полусумма(a,b,c), позволяющий определить полусумму оснований трапеции (a, b – основания, с – результат выполнения предиката). Для получения полусуммы сначала вычисляется сумма оснований с помощью стандартного предиката СЛОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных формулой Арг1+Арг2=Арг3. Для деления полученного результата сложения  на 2 используется  уже описанный ранее стандартный предикат УМНОЖЕНИЕ (Арг1, Арг2, Арг3), который вызывается со следующим набором аргументов УМНОЖЕНИЕ(c,2,z) (z – полученная ранее сумма оснований, c – результат ее деления на 2). После нахождения полусуммы оснований, полученный результат умножается на высоту трапеции: УМНОЖЕНИЕ(с,h,S) (с – полусумма основфаний, h – высота трапеции, S – площадь трапеции)

На языке Пролог-Д описанные выше утверждения могут быть представлены в следующем виде:

площадь_параллелограмма(a,h,S)<- УМНОЖЕНИЕ(a,h,S);

площадь_треугольника(a,h,S)<- УМНОЖЕНИЕ(a,h,b), УМНОЖЕНИЕ(S,2,b);

полусумма(a,b,c)<- СЛОЖЕНИЕ(a,b,z),УМНОЖЕНИЕ(c,2,z);

площадь_трапеции(a,b,h,S)<-полусумма(a,b,с),УМНОЖЕНИЕ(с,h,S);

Так как использованные для арифметических вычислений стандартные предикаты СЛОЖЕНИЕ и УМНОЖЕНИЕ в качестве аргументов могут иметь как целочисленный, так и вещественный тип, то и аргументы предикатов вычисления площадей всех трех фигур могут быть и целочисленными и вещественными. Иными словами, задаваемые параметры фигур и вычисленная площадь могут быть не только целочисленными, но и вещественными.

В качестве примера приведем вычисление площадей нижеприведенных фигур: треугольника с основанием 6,4 и высотой 3,8; параллелограмма со стороной 9 и высотой 3: трапеции с основаниями 5 и 7, высотой 4,7. Для этого к полученной базе знаний зададим вопросы:

?площадь_треугольника(6.4,3.8,S);

?площадь_параллелограмма(9,3,P);

?площадь_трапеции(7,5,4.7,T);

Ответ системы Пролог-Д:

S=12.16

P=27

T=28.2

2.2.3. Опишите вычисление пощади круга и длины окружности. Какова точность вычисления этих величин? Можно ли вычислить радиус круга по длине окружности?

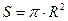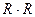Площадь круга вычисляется по формуле  , где R – радиус круга. Предикат, который выполняется, если найдена площадь окружности будет иметь имя площадь_окружности и иметь два аргумента: R – радиус круга, S – вычисленная площадь. При выполнении программы сначала вычисляется квадрат радиуса как произведение  с помощью стандартного предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных между собой соотношением Арг1*Арг2=Арг3. Для вычисления этого произведения стандартный предикат вызывается со  следующим набором аргументов  УМНОЖЕНИЕ(R,R,s), где R – радиус круга, s – результат выполнения умножения. Далее полученное произведение умножается на p=3,1415. Для этого вызывается  тот же стандартный предикат: УМНОЖЕНИЕ(3.1415,s,S) (S – площадь круга).

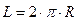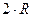Длина окружности вычисляется по формуле  , где R – радиус окружности. Предикат, который выполняется, если найдена длина окружности будет иметь имя длина_окружности1 и иметь два аргумента: R – радиус окружности, L – вычисленная длина окружности. При выполнении программы сначала вычисляется удвоенный радиус как произведение  с помощью стандартного предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных между собой соотношением Арг1*Арг2=Арг3. Для вычисления этого произведения стандартный предикат вызывается со  следующим набором аргументов  УМНОЖЕНИЕ(2,R,I), где R – радиус окружности, I – результат выполнения умножения. Далее полученное произведение умножается на p=3,1415. Для этого вызывается  тот же стандартный предикат: УМНОЖЕНИЕ(3.1415,I,L) (L – длина окружности).

По известной длине окружности можно найти ее радиус воспользовавшись формулой 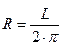. Однако это невозможно сделать с помощью предиката длина_окружности1, так как в ходе его выполнения будет вызван стандартный предикат с двумя не конкретизированными переменными в качестве аргументов УМНОЖЕНИЕ(2,R,I), что приведет к ошибке в программе. Поэтому для вычисления радиуса окружности по ее длине используется другой предикат длина_окружности2, который отличается от предиката длина_окружности1 только порядком следования действий, что исключает ошибку.

Для того, чтобы вычислять длину окружности по заданному радиусу и радиус – по заданной длине с помощью одного предиката, можно несколько модифицировать программу. Для этого вводиться новый предикат с именем длина_окружности и двумя параметрами R – радиусом окружности, L – ее длиной. В программе сначала определяется какой из заданных аргументов не конкретизирован, а затем вызывается соответствующий предикат длина_окружности1 или длина_окружност2. Если не инициализирован первый аргумент предиката, то вызывается длина_окружности2, если не конкретизирован второй, то вызывается предикат длина_окружности1. Определение, является ли переменная конкретизированной осуществляется при помощи стандартного предиката  ПЕР(Арг1), который истинен, если Арг1 – не конкретизированная переменная, а иначе ложен.

Описанная программа будет иметь вид:

площадь_круга (R,S)<-УМНОЖЕНИЕ(R,R,s),УМНОЖЕНИЕ(3.1415,s,S);

длина_окружности1(R,L)<-УМНОЖЕНИЕ(2,R,l), УМНОЖЕНИЕ(3.1415,l,L);

длина_окружности2(R,L)<-УМНОЖЕНИЕ(3.1415,l,L),УМНОЖЕНИЕ(2,R,l);

длина_окружности(R,L)<-ПЕР(L),длина_окружности1(R,L);

длина_окружности(R,L)<-ПЕР(R),длина_окружности2(R,L);

Использованные для арифметических вычислений стандартные предикаты СЛОЖЕНИЕ и УМНОЖЕНИЕ в качестве аргументов могут иметь как целочисленный, так и вещественный тип, значит аргументы предикатов вычисления площади круга и длины окружности могут быть и целочисленными и вещественными. Однако для их вычисления используется число p, которое не может быть определено точно. В программе p задано с точностью до четвертого знака после запятой и   равно 3,1415. Следовательно, полученные результаты будут иметь такую же точность.

 В качестве примера приведем нахождение площади круга радиуса 3, длины окружности радиуса  10  и  радиуса окружности с длиной 30. Для этого к полученной базе знаний зададим вопросы:

?площадь_круга(3,S);

?длина_окружности(10,L);

?длина_окружности(R,30);

Ответ системы Пролог-Д:

S=28.2735

L=62.83

R=4.77479

Рекурсия

Рекурсия является мощным методом программирования. В языке Пролог-Д она приобретает особый смысл, так как здесь отсутствуют циклические конструкции, присущие другим языкам программирования. Еще одним важным достоинством рекурсивного решения задач в Прологе-Д является то, что с ее помощью можно решать широкий класс задач.

2.3.2.Написать на языке Пролог-Д базу знаний, описывающую вычисление сумы чисел натурального ряда.

Предикат, который выполняется, если найдена сумма чисел натурального ряда будет иметь имя СУММА и два аргумента: длина ряда n и значение суммы S. Для вычисления сумму чисел натурального ряда используются следующие соображения. Во-первых,  сумма ряда, состоящего из 0 элементов равна 0. Во-вторых, для того, чтобы посчитать сумму ряда длиной в n чисел надо к сумме ряда, состоящего из (n-1) чисел, прибавить n.

Второе утверждение реализуется с помощью рекурсивного вызова. На Прологе-Д данное задание реализуется следующим образом:

СУММА(0,0)<-!;

СУММА(n,S)<-СЛОЖЕНИЕ(b,1,n),СУММА(b,T),СЛОЖЕНИЕ(n,T,S);

Для вычисления суммы в программе использовался стандартный предикат СЛОЖЕНИЕ(Арг1, Арг2, Арг3), имеющий три аргумента, связанных формулой Арг1+Арг2=Арг3.

Примером работы программы может служить вычисление суммы чисел натурального ряда: 1, 2, 3, 4, 5, 6, 7, 8, 9. Для этого к созданной базе знаний нужно задать вопрос ?СУММА(9,S);

Ответ системы Пролог-Д:

 S=45

2.3.4. Описать вычисление наименьшего общего кратного.

Для вычисления наименьшего общего кратного воспользуемся следующим равенством: x*y=НОД(x,y)*НОК(x,y), где  x, y – натуральные  числа, НОД(x,y)- наибольший общий делитель этих чисел, НОК(x,y) – наименьшее общее кратное. То есть наименьшее общее кратное находиться по формуле НОК(x,y)=(x*y)/НОД(x,y). Наибольший общий делитель вычисляется в программе рекурсивно. Предикат, который выполняется, если наибольший общий делитель двух чисел будет иметь имя nod и три аргумента: числа X,Y и результат Z. Для вычисления НОД используются следующие соображения. Во-первых, если числа равны между собой, то и результат будет иметь то же  значение. Во-вторых, нужно вычислить наибольший общий делитель для меньшего числа и разности заданных чисел, т.е. если X>Y, то вычисляется НОД для Y и X-Y, если Y>X, то для X и Y-X. Для вычисления наименьшего общего кратного используется предикат с именем nok и тремя аргументами: числами X,Y и результатом Z. На Прологе-Д все эти утверждения могут быть записаны следующим образом:

nod(X,X,X);

nod(X,Y,Z)<-БОЛЬШЕ(X,Y),СЛОЖЕНИЕ(U,Y,X),nod(U,Y,Z);

nod(X,Y,Z)<-БОЛЬШЕ(Y,X),СЛОЖЕНИЕ(U,X,Y),nod(U,X,Z);

nok(X,Y,Z)<-УМНОЖЕНИЕ(X,Y,P),nod(X,Y,U), УМНОЖЕНИЕ(Z,U,P);

Для вычисления суммы в программе использовался стандартный предикат СЛОЖЕНИЕ (Арг1, Арг2, Арг3), имеющий три аргумента, связанных формулой Арг1+Арг2=Арг3. Для вычисления умножения и деления используется стандартный предикат УМНОЖЕНИЕ(Арг1, Арг2, Арг3), имеющий три аргумента, связанных формулой Арг1*Арг2=Арг3. Если надо посчитать c=a*b, то вызывается предикат со следующим набором предикатом УМНОЖЕНИЕ(a,b,c). Если надо посчитать c=a/b, то вызывается предикат со следующим набором предикатом УМНОЖЕНИЕ(c,b,a).

Примером работы программы может служить нахождение наименьшего общего кратного чисел 18 и 222. Для этого к созданной базе знаний нужно задать вопрос ?nok(18,222,Z);

Ответ системы Пролог-Д:

 Z=666

Графические возможности системы Пролог-Д

Графические возможности системы Пролог-Д очевидно могут быть использованы в рамках решения каких-то задач: внутри экспертных систем, для вывода пользователю полученных результатов, при создании пользовательских интерфейсов.

2.4.2. Используя рекурсивное определение, напишите базу знаний, описывающую многоэтажный дом.

В программе использованы стандартные предикаты СЛОЖЕНИЕ(Арг1,Арг2,Арг3), ЛИНИЯ(Арг1,Арг2,Арг3,Арг4,Арг5) и ЗАПИСЬ_В("grp:"). С помощью предиката СЛОЖЕНИЕ может быть вычислена сумма c=a+b, для чего этот предикат вызывается в  виде СЛОЖЕНИЕ(a,b,c), и разность c=a-b: СЛОЖЕНИЕ(c,b,a). Предикат ЛИНИЯ позволяет построить отрезок с начальной точкой (Арг1, Арг2), конечной (Арг3, Арг4) и цветом Арг5.

Предикат ЗАПИСЬ_В("grp:") открывается файл графического вывода.

В программе использовано несколько дополнительных предикатов:

-     предикат прямоугольник(x,y,z,t), где (x,y), (z,t) – координаты концов диагонали прямоугольника

-     предикат треугольник(x,y,z,t), строящий равносторонний треугольник, (x,t), (z,t) - координаты основания треугольника, ((x+y)/2,z) –координата его вершины;

-     предикат блок(x,y) рисует контур этажа по заданной координате левого верхнего угла;

-     предикат окно(x,y) рисует контур окна по заданной координате левого его верхнего угла;

-     предикат окно_подъезда(x,y) рисует подъездное окно по заданной координате левого верхнего угла этажа;

-     предикат дверь(x,y) рисует подъездную дверь по заданной координате левого верхнего угла этажа;

-     предикат окна (x,y) рисует четыре окна на этаже по заданной координате левого верхнего угла этажа;

-     предикат этаж(x,y) рисует контур этажа и окна, вызывая последовательно предикаты блок(x,y), окна (x,y), окно_подъезда (x,y);

-     предикат этаж_1(x,y) рисует первый этаж дома, вызывая последовательно предикаты блок(x,y), окна (x,y), дверь(x,y);

-     предикат крыша(x,y) рисует крышу с помощью предиката треугольник по заданной координате левого верхнего угла последнего этажа;

Для рекурсивного построения используется предикат здание(x,y,n),(x,y – координаты левого верхнего угла последнего этажа, n – количество этажей), который сначала рисует верхний этаж, а затем строит здание с n-1 этажем. Если аргумент n=1, то строиться первый этаж. Для конечного построения дома используется предикат дом(n) (n- количество). Этот предикат сначала открывает файл графического вывода, затем рисует крышу и само здание дома.

Описанные утверждения реализованы в нижеприведенной программе:

прямоугольник(x,y,z,t)<-ЛИНИЯ(x,y,x,t,1),ЛИНИЯ(x,y,z,y,1),ЛИНИЯ(x,t,z,t,1),ЛИНИЯ(z,y,z,t,1);

треугольник(x,y,z,t)<-ЛИНИЯ(x,t,z,t,1), СЛОЖЕНИЕ(x,z,b),УМНОЖЕНИЕ(a,2,b),ЛИНИЯ(x,t,a,y,1),ЛИНИЯ(z,t,a,y,1);                              

блок(x,y)<-СЛОЖЕНИЕ(x,200,z),СЛОЖЕНИЕ(y,40,t),прямоугольник(x,y,z,t);

окно(x,y)<-СЛОЖЕНИЕ(x,16,z),СЛОЖЕНИЕ(y,20,t),прямоугольник(x,y,z,t);

окна(x,y)<-СЛОЖЕНИЕ(x,20,z),СЛОЖЕНИЕ(x,56,w),

СЛОЖЕНИЕ(x,128,u),СЛОЖЕНИЕ(x,164,v),

                  СЛОЖЕНИЕ(y,10,t),окно(z,t),окно(w,t),окно(u,t),окно(v,t);

окно_подъезда(x,y)<-СЛОЖЕНИЕ(x,88,w),СЛОЖЕНИЕ(x,112,z),СЛОЖЕНИЕ(y,10,r),

СЛОЖЕНИЕ(y,20,t),прямоугольник(w,r,z,t);

дверь(x,y)<-СЛОЖЕНИЕ(x,92,w),СЛОЖЕНИЕ(x,108,z),

                     СЛОЖЕНИЕ(y,10,r),СЛОЖЕНИЕ(y,40,t), прямоугольник(w,r,z,t);

этаж(x,y)<-блок(x,y),окна(x,y),окно_подъезда(x,y);

этаж_1(x,y)<-блок(x,y),окна(x,y),дверь(x,y);

крыша(x,y)<-СЛОЖЕНИЕ(w,10,x),СЛОЖЕНИЕ(x,210,z),

                       СЛОЖЕНИЕ(r,20,y),треугольник(w,r,z,y);

здание(x,y,1)<-этаж_1(x,y);

здание(x,y,n)<-этаж(x,y),СЛОЖЕНИЕ(m,1,n),СЛОЖЕНИЕ(y,40,t),здание(x,t,m);

дом(n)<-ЗАПИСЬ_В("grp:"),крыша(50,50), здание(50,50,n);

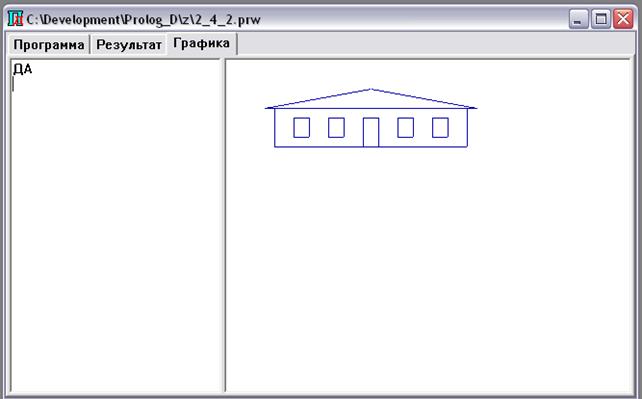
 Примером выполнения программы может служить построение одноэтажного дома. Для этого к созданной базе знаний надо задать вопрос дом(1);

 

Ответ системы Пролог-Д будет

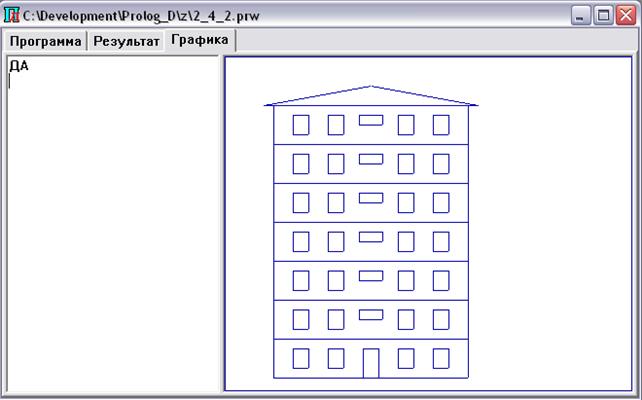
Еще одним примером выполнения программы может служить построение одноэтажного дома. Для этого к созданной базе знаний надо задать вопрос дом(7);

Ответ системы Пролог-Д будет

Обработка списков

Задачи, связанные с обработкой списков на практике встречаются довольно часто.

2.5.2. Напишите базу знаний, описывающую обращение списка (первый элемент становиться последним).

Обращение списка можно представить в виде  переписывания его элементов, начиная с головы списка,  в голову изначально пустого списка.

         Такую задачу можно списать с помощью следующих выражений:

-     основная ситуация состоит в том, что если в хвост пустого списка дописать некоторый список, то результат будет равен второму списку.

-     рекурсивна ситуация состоит в том, что первый список будет в обратном порядке дописан ко второму, если его голова будет добавлена в голову второго списка,  а его хвост будет в обратном порядке дописан к измененному второму списку.

Эти выражения реализуются в предикате присоединить(Арг1, Арг2, Арг3) с тремя аргументами, где  Арг1 – исходный список, Арг2 – список, к которому дописываются элементы, Арг3 – результирующий список.

В программе также присутствует еще два предиката. Первый из них предназначен для переписывания голова первого списка в голову второго. Этот предикат имеет имя добавить и тру аргумента: добавить (Арг1, Арг2, Арг3), где Арг1 – первый список, Арг2 – список, к которому необходимо дописать голову первого списка, Арг3 – измененный второй список.

Второй предикат предназначен для  запуска программы: обратить(R,S), где R – исходный список, S – результирующий список. Этот предикат является стартом рекурсии. Он вызывает предикат присоединить с аргументами, инициализированными следующим образом: присоединить (R,[],S).

Описанные  утверждения будут иметь вид следующей программы:

добавить(X,Y,[X|Y]);

присоединить([],Y,Y);

присоединить([X|T],Y,S)<-добавить(X,Y,Z), присоединить(T,Z,S);

обратить(R,S)<-присоединить(R,[],S);

В качестве примера получим список, обратный списку [1,2,3,4,5,6]. Для этого к созданной базе знаний нужно задать вопрос ?обратить([1,2,3,4,5,6],S);

Ответ системы Пролог-Д будет

S=[6,5,4,3,2,1]

Заключение

В ходе выполнении работы на языке Пролог-Д были созданы базы знаний для отдельных заданий. Базы знаний  реализовывались с использованием таких понятий, как факты, правила, рекурсия. Для выполнения отдельных подзадач использовались стандартные предикаты системы Пролог-Д.

В качестве отдельных структур данных был рассмотрен список.

Базы знаний  реализовывались с использованием таких понятий, как факты, правила, вопросы. Для выполнения отдельных подзадач использовались встроенные стандартные предикаты системы Пролог-Д, позволяющие производить арифметические вычисления, строить графические объекты, управлять логическим выводом, контролировать типы данных и т.д.

На примере двух заданий - вычисление сумы чисел натурального ряда и вычисление наименьшего общего кратного, ознакомились с таким понятием как рекурсия. Также были рассмотрены графические возможности системы Пролог-Д в задании построения многоэтажного дома.

В качестве отдельной структуры данных был рассмотрен список, для которого была реализована программа его обращения.

Список литературы

1.     Абдикеев Н.М. Проектирование интеллектуальных систем в экономике. Учебник/М.: Экзамен, 2004, - 526с.

2.     Алексеев М.Н., Бешенков С.А., Гейн А.Г., Григорьев С.Г. Информатика и информационные технологии: практические работы / Миасс, 2000 – 42с.

3.     Доорс Дж., Рейблейн А., Вадера С. Пролог – язык программирования будущего / М.: Финансы и статистика, 1990 – 144 с.

4.     Гаврилова Т.А., Хорошевский В.Ф. Базы знаний интеллектуальных систем. Учебник / С-П.:Питер, 2000 – 382 с.

5.     Романов В.П. Интеллектуальные информационные системы в экономике. Учебник / М:. Экзамен, 2003 – 494 с.