Задача 2
Необходимо оценить работу
АТС, которая имеет n линий связи.
Моменты поступления вызовов
на станцию являются случайными и независимыми друг от друга.
Средняя плотность потока
равна λ вызовов в единицу времени.
Продолжительность каждого
разговора является величиной случайной и подчинена показательному закону
распределения.
Среднее время одного
разговора равно tабс единиц времени.
Решение:
n = 8;
λ = 4;
tабс = 1.
Для начала вычислим
финальные вероятности состояний СМО
(вероятности числа занятых линий связи).
Воспользуемся следующими
формулами:
…
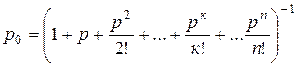
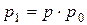
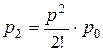
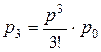
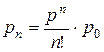, где р = λ tабс.
Р = 4*1 = 4
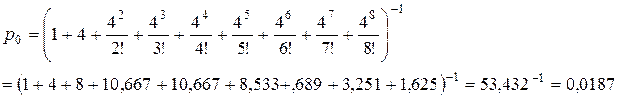
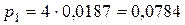
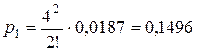
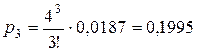
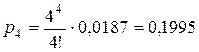
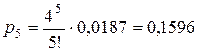
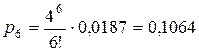
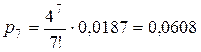
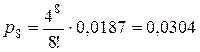
Теперь вычислим
характеристики эффективности СМО.
Вероятность того, что
пришедшая заявка получит отказ (не будет обслужена): Ротк = рn = p8 = 0,0304.
Относительная пропускная
способность (вероятность того, что заявка будет обслужена): Q = 1 – pотк = 1 – 0,0304 = 0,9696.
Абсолютная пропускная
способность: А = λ * Q = 4 *
0.9696 = 3.8784.
Среднее число занятых
каналов:
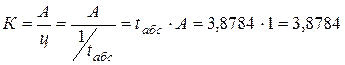
В целом, можно сделать
вывод о достаточно эффективной работе АТС. Из 8-ми каналов занято в среднем
около четырех, а из поступающих заявок остаются не обслуженными лишь 3,04%.
Задача 4
На столовом графике
цифры у стрелок показывают в числителе –
продолжительность работы в днях, в знаменателе – количество ежедневно занятых работников на ее выполнение.
В распоряжении организации,
выполняющей этот комплекс работ, имеется 23 рабочих, которых необходимо
обеспечить непрерывной и равномерной работой.
Используя имеющиеся запасы
времени по некритическим работам, скорректируйте сетевой график с учетом
ограничения по качеству рабочих.
Решение:
Для начала определим
критический путь и имеющийся ресурс времени:
|
События
|
Сроки совершения событий
|
Резерв
|
|
Ранний
|
Поздний
|
|
1
2
3
4
5
|
0
4
13
15
18
|
0
10
13
15
18
|
0
6
0
0
0
|
Критический путь равен 18
дням.
Скорректированный сетевой
график.
Распределение работников по
видам работ:
|
7
|
1→3
|
|
5
|
1→3→4
|
|
3
|
1→3→4→5
|
|
1
|
4→5
|
|
6
|
1→5
|
|
1
|
2→5
|
Общая сумма составляет 23.
Σ = 23.
Задание 4
Решение
Рассчитаем основные
параметры сетевого графика:
|
Код
работы i-j
|
tij
|
tijpн
|
tijpо
|
tijnm
|
tijno
|
Rij
|
rij
|
|
1-2
|
4
|
0
|
4
|
8
|
12
|
8
|
0
|
|
1-3
|
13
|
0
|
13
|
0
|
13
|
0
|
0
|
|
1-5
|
6
|
0
|
6
|
12
|
18
|
12
|
12
|
|
2-4
|
3
|
4
|
7
|
12
|
15
|
8
|
8
|
|
3-4
|
2
|
13
|
15
|
13
|
15
|
0
|
0
|
|
3-5
|
5
|
13
|
18
|
13
|
18
|
0
|
0
|
|
4-5
|
3
|
15
|
18
|
15
|
18
|
0
|
0
|
Критический путь равен 18.
Срорректированный график: