Содержание
Задача 1. 3
Задача 2. 4
Задача 3. 4
Задача 4. 6
Задача 5. 6
Задача 7. 7
Задача 7. 9
Задача 8. 10
Список литературы.. 11
Задача 1
Какой толщины слой меди выделится на катоде за 5 часов из
раствора сульфита меди (СuSO4),
если электролиз протекает при силе тока 1,5 А.
Согласно законам Фарадея: 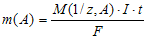
где т(А) — масса вещества А, окисленного или
восстановленного на электроде (г); М(1/z,А) — молярная масса эквивалента
вещества А (г/моль); I — сила тока (А); t — продолжительность электролиза (с);
F – число Фарадея, (F ≈ 96500 Кл/моль). Молярная масса эквивалента меди в
СuSO4 равна:
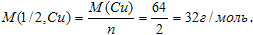
Подставив в формулу значения М(1/2,Cu) получим:
m (Cu) = 32*1.5*5/965000 =
2.49*10-4 г
Массу меди можно выразить через объем:
m=r V=r Sd
Плотность тока i = I/S, где S — площадь покрытия. Откуда I= iS, a т = kiSt.
Плотность меди равна (г): 8,96 г/см3 = 8960 кг/м3
Электрохимический эквивалент меди (к) равен 1,1857 г/А • ч.
= 3,29*10-4 г/Кл
Приравняв массы, получим: kiSt = r Sd,
отсюда d=kit/r
Найдем плотность тока:
т = kiSt = kIS,
IS =
г/k = 8 960/3,29*10-4
= 2723,4*104 А с /м2
S = 2
723,4*104 /1.5 = 1 815,6 с /м2
i = I/S =
1.5/1815,6= 8,26*10-4 г/Кл
d=kit/r =
3,29*10 -4 *8,26*10-4*5*3600
/ 8960 = 5*10-7 м
Задача 2
Площадку в 250 см2 расположенную в вакууме под
углом 600 к направлению магнитного поля пронизывает магнитный поток
1,2 МВб. Найти индукцию и напряженность поля.
Магнитным потоком Φ через площадь S контура называют
величину
Φ = B · S · cos α,
где B – модуль вектора магнитной индукции, α – угол
между вектором 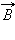 и нормалью
и нормалью
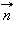 к
плоскости контура
к
плоскости контура
Φ = B · S · cos α,
В = Ф/ S · cos α = 1,2*106 /
0,025*0,5 = 96*106
Вектором напряженности Н электрического
поля в точке Q называется вектор силы, действующей на электрически заряженную
неподвижную частицу, помещенную в точку Q , если эта частица имеет единичный
положительный заряд.

Н = 1,2*106 / 1,26*10-6 = 0,95*1012
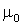 -
абсолютная магнитная проницаемость вакуума (основная магнитная постоянная);
-
абсолютная магнитная проницаемость вакуума (основная магнитная постоянная); 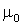 = =
1,26*10-6Гн/м
= =
1,26*10-6Гн/м
Задача 3
Написать уравнение гармонического колебания 8 см с периодом
0,2 с от начала колебаний.
Прежде чем
перейти к решению данной задачи, нужно дать понятие гармоническим колебаниям и
написать уравнение гармонических колебаний в общем виде.
Гармонические
колебания - это такие колебания, при которых колеблющаяся величина x изменяется
со временем по закону синуса, либо косинуса:
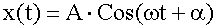 ,
,
или
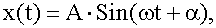
где A -
амплитуда; ω - круговая частота; α - начальная фаза; ( ωt +
α ) - фаза.
Фаза колебания
- это аргумент гармонической функции: ( ωt + α ). Начальная фаза
α - это значение фазы в начальный момент времени, т.е. при t = 0.
Амплитуда
колебания A - это наибольшее значение колеблющейся величины.
При
изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к
прежнему значению. Найдем промежуток времени T, в течение которого фаза
гармонической функции изменяется на 2π .
ω(t + T)
+α = ωt + α + 2π,
или
ωT =
2π.
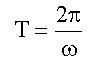 .
.
Время T одного
полного колебания называется периодом колебания. Частотой ν называют
величину, обратную периоду
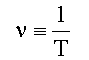 .
.
Единица
измерения частоты - герц (Гц), 1 Гц = 1 с-1.
Так как
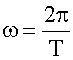 ,
,
то
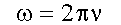 .
.
Таким образом,
X=Xm*сos(wt-фo)
Хm – амплитуда колебаний, по условию задачи она равна 8 см
или 0,1 м в СИ.
w - частота =2 π/Т= 2*3,14/0,2= π/10
фo - начальная фаза -- по условии задачи равна нулю
wt-фo - фаза
Итак получаем
Х = 0.1cos((π/10)*t)
Задача 4
Магнитная стрелка расположена под проводником вдоль него.
При каком направлении тока в проводнике стрелка повернется к читателю?
Согласно правилу левой руки (рис.1):
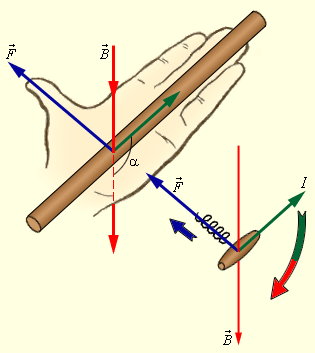
Рисунок 1.
Правило левой руки и правило буравчика.
Для определения направления силы
Ампера 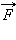 удобно пользоваться правилом буравчика: воображаемый буравчик
располагается перпендикулярно плоскости, содержащей вектор
удобно пользоваться правилом буравчика: воображаемый буравчик
располагается перпендикулярно плоскости, содержащей вектор 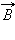 и проводник
с током, затем его рукоятка поворачивается от направления тока к направлению
вектора
и проводник
с током, затем его рукоятка поворачивается от направления тока к направлению
вектора 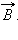 Поступательное
перемещение буравчика будет показывать направление силы Ампера
Поступательное
перемещение буравчика будет показывать направление силы Ампера 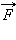
Задача 5
Длина световой волны в данной среде 0,56 мкм, а в другой
0,44 мкм. Какова скорость света в данной среде, если во второй она равна 2,2*108
м/с.
Между длиной волны и скоростью света существует следующее соотношение:
λ1 = с1/ν1
λ2 = с2/ν1
λ1/ λ2
= с1/ с2
Тогда с1 = λ1
с2 / λ2 =
0,56*2,2*108 / 0,44 = 2,8*108 м/с.
Задача 7
Какое явление положено в основу действия трансформатора?
Можно ли включать трансформатор в цепь постоянного тока? Дать объяснение, что
переносится волной: вещество или энергия?
В основе действия трансформатора
лежит явление электромагнитной индукции. Трансформатор состоит из одной
первичной обмотки (ПО), одной или нескольких вторичных обмоток (ВО) и
ферромагнитного сердечника (магнитопровода), обычно замкнутой формы. Все
обмотки расположены на магнитопроводе и индуктивно связаны между собой. Иногда
вторичной обмоткой служит часть ПО (или наоборот); такие трансформаторы
называются автотрансформаторами. Концы ПО (вход трансформатора) подключают к
источнику переменного напряжения, а концы ВО (его выход) - к потребителям.
Переменный ток в ПО приводит к появлению в магнитопроводе переменного
магнитного потока. В реальных трансформаторах часть магнитного потока
замыкается вне магнитопровода, образуя так называемые потоки рассеяния; однако
в высококачественные трансформаторы потоки рассеяния малы по сравнению с
основным потоком (потоком в магнитопроводе).
Принцип работы трансформатора. Возбуждение ЭДС индукции в
одном контуре за счет изменения тока в другом контуре может быть нежелательным
(например, в радиотехнических устройствах такие паразитные ЭДС представляют
серьезную проблему). Однако существуют и устройства, основанные на этом явлении
и приносящие большую пользу.
Напряжение, генерируемое в первичной обмотке трансформатора,
имеющей число витков, равное Nперв и подключенной к цепи переменного тока,
равно
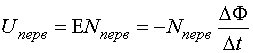
Вторичная обмотка с числом витков Nвтор пронизывается тем же
потоком магнитной индукции, поэтому
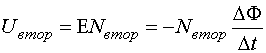
Отсюда: отношение напряжений на первичной и вторичной
обмотках трансформатора равно отношению числа витков в этих обмотках и
вторичное напряжение
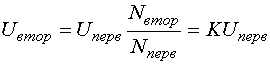
Коэффициент K называется коэффициентом трансформации.
Итак, если число витков во вторичной обмотке больше числа
витков в первичной обмотке ( K > 1), то трансформатор - повышающий
(вторичное напряжение больше первичного). При K < 1 трансформатор
понижающий.
Если пренебречь потерями на нагревание сердечника
трансформатора (в реальных трансформаторах КПД достигает 99%), то мощность,
выделяемая в первичной цепи, N = UпервIперв, должна по закону сохранения
энергии равняться мощности, выделяемой во вторичной цепи трансформатора, т.е.
UпервIперв = UвторIвтор, откуда
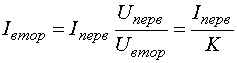 Итак, ток во вторичной цепи повышающего трансформатора становится меньше, чем
ток в первичной обмотке. Это обстоятельство используется на практике при
передаче энергии на большие расстояния. Генераторы электростанций вырабатывают
ток большой силы и невысокого напряжения. На выходных повышающих
трансформаторах электростанций напряжение повышается во много раз (до
нескольких сотен тысяч вольт). При этом уменьшается ток в цепи, что приводит к
уменьшению джоулевых потерь при передаче тока на большие расстояния. На конце
цепи тока, подключенном к потребителям, понижающие трансформаторы уменьшают
напряжение переменного тока до стандартного значения, при этом ток в цепи
увеличивается.
Итак, ток во вторичной цепи повышающего трансформатора становится меньше, чем
ток в первичной обмотке. Это обстоятельство используется на практике при
передаче энергии на большие расстояния. Генераторы электростанций вырабатывают
ток большой силы и невысокого напряжения. На выходных повышающих
трансформаторах электростанций напряжение повышается во много раз (до
нескольких сотен тысяч вольт). При этом уменьшается ток в цепи, что приводит к
уменьшению джоулевых потерь при передаче тока на большие расстояния. На конце
цепи тока, подключенном к потребителям, понижающие трансформаторы уменьшают
напряжение переменного тока до стандартного значения, при этом ток в цепи
увеличивается.
Трансформатор нельзя включать в цепь постоянного тока.
Электромагнитные волны в траснформаторе переносят энергию.
При распространении волн возникает поток электромагнитной энергии.
Задача 7
Работа выхода электронов у хлористого натрия составляет 4
эв. Излучение какой длины волны способно вызвать эффект в этом веществе?
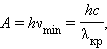
где c – скорость света, λкр – длина волны,
соответствующая красной границе фотоэффекта
Отсюда λкр = hc/A
h = 4,136·10–15 эВ·с.
c = 3.8*108м/c
λкр = hc/A = 4,136*10-15*3,8*108/4
= 3,92*10-7 м
Задача 8
Прочитать и объяснить ядерную реакцию
24He → 01n + 714N
В данной реакции происходит распад ядра гелия на ядро азота
и протоны. В результате столкновения частиц происходит распад ядра с
образованием протонов и выделением значительной кинетической энергии.
Список литературы
1.
Марон В.Е. и др. Физика (законы, алгоритмы решения
задач. — СПб: "Специальная Литература", 1997.
2.
Окунь Л.Б. Физика элементарных частиц. М.: Наука, 1988.
3.
Широков Ю.М., Юдин Н.П., Ядерная физика, 2 изд., М.,
1980
4.
Девис С, Джеймс А. Электрохимический словарь. М.: Мир,
1979.
5.
Химия / Под ред. В. Шретера . – М.: Химия, 1986. – 648 с.