КАФЕДРА СТАТИСТИКИ

О Т Ч Е Т

о результатах выполнения

компьютерной лабораторной работы №1

«Автоматизированный априорный анализ статистической совокупности

 в среде MS Excel»

Вариант № 1010

                                                                 Выполнил: ст. III курса  

                                                                                   Проверил:

                                                      Калуга

                                                        2006

Постановка задачи

При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию  (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и  о выпуске продукции за год.

В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.

Для проведения автоматизированного статистического анализа совокупности выборочные данные представлены в формате электронных таблиц процессора Excel в диапазоне ячеек B4:C35. Выборочные данные приведены в табл. 1.

Таблица 1

Исходные данные

В процессе исследования совокупности необходимо решить ряд статистических задач для выборочной и генеральной совокупностей.

Статистический анализ выборочной совокупности

1.    Выявить наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения.

2.    Рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую (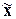), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(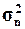), средние отклонения – линейное (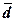) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии  К.Пирсона (Asп).

3.    На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценить:

а) степень колеблемости значений признаков в совокупности;

б) степень однородности совокупности по изучаемым признакам;

в) устойчивость индивидуальных значений признаков;

г) количество попаданий индивидуальных значений признаков в диапазоны (), (), ().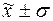

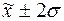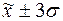4.    Дать сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:

а) вариации признаков;

б) количественной однородности единиц;

в) надежности (типичности) средних значений признаков;

г) симметричности распределений в центральной части ряда.

5.    Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.

Статистический анализ  генеральной совокупности

1.               Рассчитать генеральную дисперсию 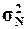, генеральное среднее квадратическое отклонение 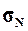 и ожидаемый размах вариации признаков R_N. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.

2.               Для изучаемых признаков рассчитать:

а) среднюю ошибку выборки;

б) предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности.

3.               Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок  сделать вывод о степени близости распределения единиц генеральной совокупности к нормальному распределению.

Задание 1

Этап 1. Выявление и удаление из выборки аномальных единиц наблюдения

Первичные данные выборочной совокупности могут содержать аномальные значения изучаемых признаков. Задание 1 заключается в их выявлении и исключении из дальнейшего рассмотрения с целью обеспечения устойчивости данных статистического анализа.

Для выявления аномальных значений этих признаков построим график, используя диаграмму рассеяния.

Диаграмма рассеяния – это точечный график, осями Х и Y которого сопоставлены два изучаемых признака единиц совокупности.

1.     Выделяем мышью оба столбца  исходных данных в диапазоне В4:С35.

2.     Вставка   Диаграмма   Точечная   Готово.

В результате выполнения этих действий на рабочем листе Excel появляется диаграмма рассеяния (рис.1).

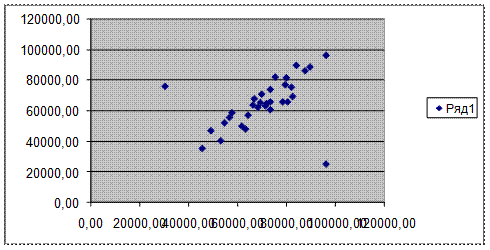
Рис. 2. Аномальные значения признаков на диаграмме рассеяния

 Этап 2. Визуальный анализ диаграммы рассеяния, выявление и фиксация аномальных значений признаков, их удаление из первичных данных

Обнаружение резко выделяющихся наблюдений производится визуально, путем выявления точек, отстоящих от основной массы точек на существенном расстоянии.

1.    Найти на графике точку, соответствующую аномальному наблюдению.

2.    Подвести курсор к точке на диаграмме рассеяния, соответствующей аномальному наблюдению. После непродолжительного времени возле точки автоматически появится надпись, содержащая значения признаков этого наблюдения в формате (Х, Y) (рис. 2).

Рис. 2.

В полученном графике можно наблюдать две аномальные точки с координатами (96130;25300) и (30350;75900).

3.    В исходных данных визуально находим в таблице 12 строку, соответствующую выявленной аномальной единице наблюдения (предприятию). Скопируем эту строку в таблицу 2.

Таблица 2

                                  Аномальные единицы наблюдения                                 

4.    Выделяем мышью всю адресную строку с данными, подлежащими удалению.

5.    Правка   Удалить.

6.    Выполняем действия с 1 по 5 до полного удаления всех аномальных наблюдений (рис. 3).

7.    Перемещаем  диаграмму рассеяния в область ячеек, начиная с ячейки F4.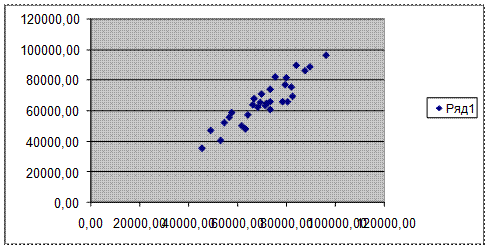

Рис. 3. Диаграмма рассеяния после удаления аномальных значений

Задание 2

Этап 1. Расчёт описательных параметров выборочной и генеральной совокупности с использованием инструмента ОПИСАТЕЛЬНАЯ СТАТИСТИКА.

Алгоритм 1.1 Расчёт описательных статистик

1.     Сервис  Анализ данных   Описательная статистика   ОК;

2.     Входной интервал 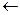 диапазон ячеек таблицы, выделенный  согласно (В4:С33) для значений признаков Стоимость основных фондов и Выпуск продукции

3.     Группирование    по столбцам;

4.     Итоговая статистика - Активизировать;

5.     Уровень надёжности - Активизировать;

6.     Уровень надёжности 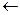 95,4

7.     Выходной интервал   адрес ячейки заголовка первого столбца   (А46:С46) (рис. 4).

8.     ОК;

9.     При появлении окна с сообщением «Выходной интервал накладывается на имеющиеся данные»  ОК.

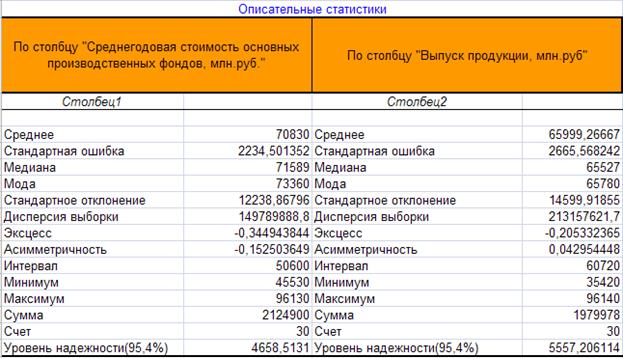
В результате указанных действий Excel осуществляет вывод описательных статистик  в заданный диапазон рабочего файла  (табл. 3).

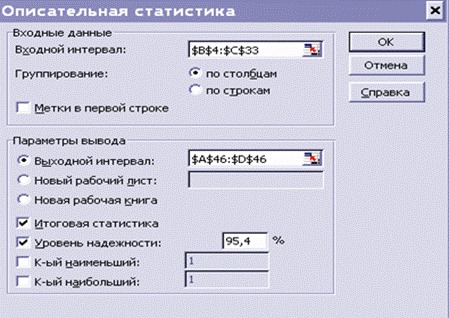
Рис.4. Диалоговое окно инструмента ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Таблица 4

Описательные статистики

Этап 2. Оценка предельных ошибок выборки для различных уровней надёжности в режиме ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Алгоритм 2.1. Расчёт предельной ошибки выборки при Р = 0,683

1.     Сервис    Анализ данных     Описательная статистика     ОК;

2.     Входной интервал – диапазон ячеек таблицы, выделенный согласно (В4:С33) для значений  признаков Стоимость основных фондов и Выпуск продукции;

3.     Итоговая статистика – Снять флажок;

4.     Уровень надёжности – Активизировать;

5.     Уровень надёжности  – 68,3;

6.     Выходной интервал  адрес ячейки, выделенный согласно (А67:С67) для предельной ошибки выборки при Р = 0,683;

7.     ОК;

8.     При появлении окна с сообщением «Выходной интервал накладывается на имеющиеся данные»  ОК.

Алгоритм 2.1. Расчёт предельной ошибки выборки при Р = 0,997

1.     Сервис    Анализ данных     Описательная статистика     ОК;

2.     Входной интервал – диапазон ячеек таблицы, выделенный согласно (В4:С33) для значений  признаков Стоимость основных фондов и Выпуск продукции;

3.     Итоговая статистика – Снять флажок;

4.     Уровень надёжности – Активизировать;

5.     Уровень надёжности  – 99,7;

6.     Выходной интервал  адрес ячейки, выделенный согласно (А75:С75) для предельной ошибки выборки при Р = 0,997;

7.     ОК;

8.     При появлении окна с сообщением «Выходной интервал накладывается на имеющиеся данные»  ОК.

В результате работы алгоритмов 2.1 и 2.2 Excel  выводит  в соответствующие ячейки табл. 4 рабочего файла значения предельных ошибок выборки при Р = 0,683 и Р = 0,997 (табл. 4а и табл. 4б).

Таблица 4а

Предельные ошибки выборки

Таблица 4б

         Предельные ошибки выборки

Этап 3. Расчёт описательных параметров выборочной совокупности        с использованием инструмента МАСТЕР ФУНКЦИЙ

Алгоритм 3.1. Расчёт выборочного стандартного отклонения 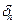 для признака  Среднегодовая стоимость основных  производственных фондов.

1.     Устанавливаем курсор в ячейку (В83) для среднего квадратического отклонения первого признака.

2.     Вставка  Функция;

3.     Статистические  СТАНДОТКЛОНП  ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения первого признака (В4:В33).

Алгоритм 3.2. Расчёт  выборочного стандартного отклонения 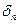  для признака Выпуск продукции

1.     Устанавливаем курсор в ячейку (D83) для среднего квадратического отклонения второго признака;

2.     Вставка  Функция;

3.     Статистические  СТАНДОТКЛОНП  ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения второго признака (С4:С33).

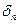
Алгоритм 3.3. Расчёт выборочной дисперсии  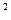 для признака Среднегодовая стоимость основных  производственных фондов.

1.     Устанавливаем курсор в ячейку (В84) для выборочной дисперсии первого признака;

2.     Вставка  Функция;

3.     Статистические  ДИСПР ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения первого признака (В4:В33).

Алгоритм 3.4. Расчёт  выборочной дисперсии 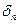 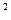 по признаку               Выпуск продукции

1.     Устанавливаем курсор в ячейку (D84) для выборочной дисперсии второго признака;

2.     Вставка  Функция;

3.     Статистические  ДИСПР ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения второго признака (С4:С33)

Алгоритм 3.5. Расчёт  выборочного среднего линейного отклонения  по признаку  Среднегодовая стоимость основных  производственных фондов.

1.     Устанавливаем курсор в ячейку (В85) для среднего линейного отклонения первого признака;

2.     Вставка  Функция;

3.     Статистические  СРОТКЛ ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения первого признака (В4:В33).

Алгоритм 3.6. Расчёт  выборочного среднего линейного отклонения  по признаку Выпуск продукции

1.     Устанавливаем курсор в ячейку (D85) для среднего линейного отклонения второго признака;

2.     Вставка  Функция;

3.     Статистические СРОТКЛ ОК;

4.     Число 1  диапазон ячеек таблицы 1, содержащей значения первого признака (С4:С33).

Алгоритм 3.7. Расчёт коэффициента вариации V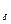 по признаку  Среднегодовая стоимость основных  производственных фондов.

1.     Устанавливаем курсор в ячейку (В86) для коэффициента вариации первого признака;

2.     В активизированную ячейку вводим формулу = D83/D48*100.

Алгоритм 3.8. Расчёт коэффициента вариации V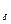 по признаку    

Выпуск продукции

1.     Устанавливаем курсор в ячейку (D86) для коэффициента вариации второго признака;

2.     В активизированную ячейку вводим формулу = D83/D48*100.

Алгоритм 3.9. Расчёт выборочного коэффициента асимметрии Пирсона Аs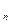 по признаку  Среднегодовая стоимость основных  производственных фондов.

1.     Устанавливаем курсор в ячейку (В87) для коэффициента асимметрии первого признака;

2.     В активизированную ячейку вводим формулу = (В48 - В51)/В83.

Алгоритм 3.10. Расчёт выборочного коэффициента асимметрии Пирсона Аs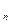 по признаку Выпуск продукции

1.     Устанавливаем курсор в ячейку (D87) для коэффициента асимметрии второго признака;

2.     В активизированную ячейку вводим формулу = (D48 - D51)/D83.

В  результате работы алгоритмов 3.1 - 3.10 Excel осуществляет вывод значений выборочных параметров 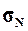  , 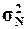,  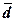,Vσ, Asп  в соответствующие ячейки рабочего листа (табл. 5).

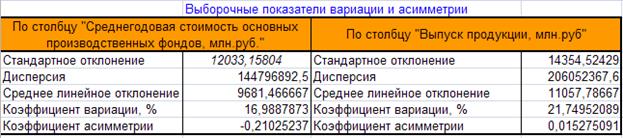
Таблица 5

Выборочные показатели вариации и асимметрии

Задание 3

Этап 1. Построение промежуточной таблицы

Алгоритм 1.1. Расчёт нижних границ интервалов

1.     Сервис  Анализ данных  Гистограмма  ОК;

2.     Входной интервал  диапазон ячеек (В4:В33) для столбца значений первого признака;

3.     Интервал карманов оставляем незаполненным;

4.     Выходной интервал  адрес заголовка первого столбца первичной промежуточной табл. 6 (А90) (рис. 5).  

5.     ОК.

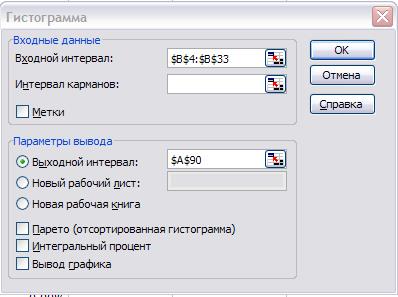
Рис. 8. Диалоговое окно инструмента Гистограмма

В результате выполнения алгоритма 1.1. получаем:

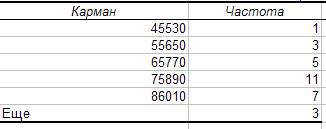
Алгоритм 1.2. переход от нижних границ к верхним

1.     Выделяем курсором верхнюю левую ячейку табл. 6 (А91) и нажимаем клавишу [Delete];

2.     Вводим в ячейку с именем «Ещё» значение x_mах первого признака из табл. 3 - Описательная статистика.

В результате выполнения алгоритма 1.2. получаем:

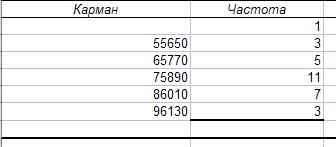
Этап 2. Генерация выходной таблицы и графиков

Алгоритм 2.1. Построение выходной таблицы, столбиковой диаграммы 

 и  кумуляты

1.     Сервис  Анализ данных     Гистограмма  ОК;

2.     Входной интервал  диапазон ячеек (В4:В33) для столбца значений первого признака;

3.     Интервал карманов  диапазон карманов итоговой промежуточной табл. 6 с верхними границами (А92:А96);

4.     Входной интервал  адрес заголовка первого столбца выходной  табл. 7 (А101);

5.     Интегральный процент - Активизировать;

6.     Вывод графика - Активизировать;

7.     ОК (рис. 7);

8.     При появлении сообщения о наложении данных – ОК.

В результате выполнения алгоритма 2.1. получаем табл. 7:

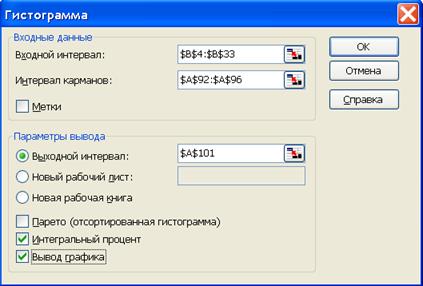
Рис. 7. Диалоговое окно инструмента Гистограмма с заполненными данными

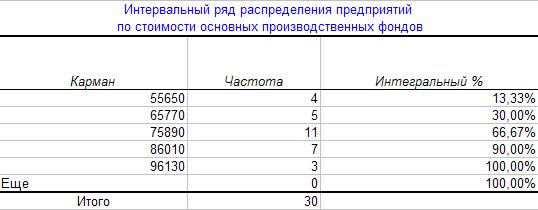
Таблица 7

Интервальный ряд распределения предприятий по стоимости

основных производственных фондов

Этап 3. Приведение выходной таблицы и диаграммы к виду, принятому в статистике

Алгоритм 3.1. Преобразование выходной таблицы в результативную

1.     Заменяем название столбцов выходной табл. 7 в соответствии с табл. 8:

Таблица 8

2.     Строки первого столбца приводим к виду «нижняя граница интервала – верхняя граница интервала», учитывая совпадение верхних границ предыдущего интервала с нижней границей последующего интервала;

3.     Строку с именем «Еще» выделяем  мышью и очищаем, нажав клавишу [Delete];

4.     Добавляем  и заполняем строку с именем «Итого».    

В результате выполнения алгоритма 2.1. получаем (рис. 8):

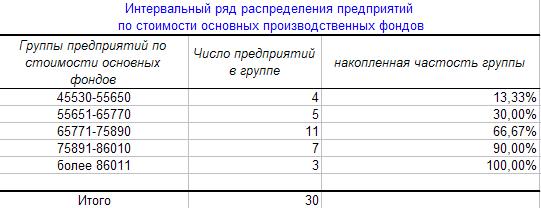
Рис. 8.  Excel –формат результативной таблицы

Алгоритм 3.2. Преобразование столбиковой диаграммы в гистограмму

1.     Осуществляем «захват мышью» и перемещаем график, расположив его вслед за табл. 7 (А112);

2.     Исключяем зазоры, выполнив следующие действия:

·        нажать правую кнопку мыши на одном из столбиков диаграммы;

·        Формат рядов данных  Параметры;

·        Ширина зазора  0;

·        ОК;

3.     Используя «захват мышью» за угол поля графика, устанавливаем соотношение ширины и высоты фигуры гистограммы в пропорции 1:0,62.

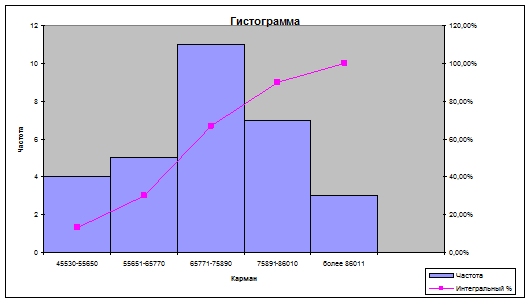
Рис. 9. Гистограмма и кумулята интервального ряда распределения

Заключительный этап

1. Анализ обобщающих показателей описательной статистики

На основании рассчитанных значений показателей описательной статистики можно не только получить информацию о средних величинах, степени вариации и особенностях формы распределения единиц совокупности, но и сделать выводы о других статистических характеристиках и свойствах совокупности, о внутренней связи между единицами совокупности.

1.1. Степень колеблемости  признака определяется по значению коэффициента вариации Vσ. Исходя из оценочной шкалы колеблемости

0% < Vσ 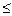   40% - колеблемость незначительная;

40% < Vσ 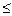  60% - колеблемость средняя (умеренная);

Vσ >  60% -  колеблемость значительная.

В нашей задаче по первому признаку  Vσ=16,9887873

  по второму Vσ=21,74952089

 , таким образом, степень колеблемости по первому и по второму признакам  незначительная.

1.2. Совокупность является количественно однородной по данным признакам, т.к. выполняется неравенство Vσ 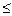 33%.

1.3. Для оценки надёжности средней величины 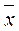 можно воспользоваться значением показателя вариации  Vσ. Так как его значение невелико, то индивидуальные значения признака х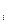 мало отличаются друг от друга, единицы наблюдения количественно однородны и, следовательно, средняя арифметическая величина 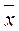 является надёжной характеристикой данной совокупности.

1.4. Сопоставление средних отклонений – квадратического σ и линейного 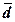  позволяют сделать вывод об устойчивости индивидуальных значений признака, т.е. об отсутствии среди них «аномальных» вариантов значений. Так как 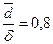 , то значения признаков устойчивы и в них  нет «аномальных»  выбросов.

1.5. Границы диапазонов рассеяния значений признаков. Так как мы имеем нормально распределённые ряды  вероятностные оценки диапазонов рассеяния значений признаков таковы:

68,3% войдёт в диапазон   ();

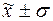95,4% попадает в диапазон ();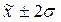

99,7% появится в диапазоне ().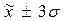

2.       Анализ типа закономерности распределения

         2.1. Так как наша гистограмма имеет одновершинную форму, есть основание предполагать, что выборка является однородной по данным признакам.

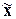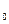         2.2. Нормальное распределение является симметричным, и для него выполняется соотношение:     = М= М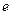, Аs = 0 , Аs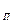= 0 , R = 6σ.

В нашей задаче  присутствует небольшое нарушение этих отношений, это свидетельствует о наличии асимметрии распределения. Распределение с небольшой или умеренной асимметрией в большинстве случаев по своему типу относится к нормальному. Таким образом, гистограмма приблизительно симметрична, её «хвосты» не очень длинны, поэтому она представляет распределение, близкое к нормальному.

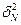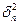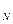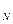         2.3. Распределение единиц  выборочной совокупности близко к нормальному, выборка является репрезентативной (значение показателей   и  расходятся незначительно) и при этом коэффициенты  Аs, Ek указывают на небольшую или умеренную величину асимметрии и эксцесса соответственно, поэтому есть основание полагать, что распределение единиц генеральной совокупности по изучаемому признаку будет близко к нормальному.