ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ
статистической совокупности
в среде MS Excel»
Вариант № 47
Выполнил:
ст. III курса гр. ФК, город
Ф.И.О.
Проверил: Берлин
Юлия Ильинична
Ф.И.О.
Архангельск,
2006 г.
Постановка задачи
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
Для
проведения автоматизированного статистического анализа совокупности выборочные
данные представлены в формате электронных таблиц процессора Excel в диапазоне
ячеек B4:C35. Для демонстрационного примера (ДП) выборочные данные приведены в
табл. 1-ДП.
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн. руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
2636,00
|
2523,50
|
|
2
|
3101,50
|
2768,50
|
|
3
|
3199,50
|
3087,00
|
|
4
|
3371,00
|
3430,00
|
|
5
|
2195,00
|
1715,00
|
|
6
|
3542,50
|
2940,00
|
|
7
|
3640,50
|
3969,00
|
|
8
|
2734,00
|
2695,00
|
|
9
|
3346,50
|
3160,50
|
|
10
|
3861,00
|
3944,50
|
|
12
|
1460,00
|
3675,00
|
|
11
|
4228,50
|
4165,00
|
|
13
|
3224,00
|
3283,00
|
|
14
|
3542,50
|
3577,00
|
|
15
|
4057,00
|
4336,50
|
|
16
|
4645,00
|
4655,00
|
|
17
|
3469,00
|
3136,00
|
|
18
|
3836,50
|
3724,00
|
|
19
|
3052,50
|
2327,50
|
|
20
|
3885,50
|
3185,00
|
|
21
|
4326,50
|
4287,50
|
|
22
|
2979,00
|
2425,50
|
|
23
|
2366,50
|
2278,50
|
|
24
|
3959,00
|
3650,50
|
|
25
|
3542,50
|
3185,00
|
|
26
|
3297,50
|
3013,50
|
|
27
|
2562,50
|
1960,00
|
|
28
|
3444,50
|
3062,50
|
|
29
|
3983,50
|
3356,50
|
|
31
|
4645,00
|
1225,00
|
|
30
|
3787,50
|
3185,00
|
|
32
|
2783,00
|
2842,00
|
В
процессе исследования совокупности необходимо решить ряд статистических задач
для выборочной
и генеральной совокупностей.
Статистический анализ выборочной совокупности
1. Выявить наличие среди
исходных данных резко выделяющихся значений признаков («выбросов» данных) с
целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать обобщающие
статистические показатели совокупности по изучаемым признакам: среднюю
арифметическую ( ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию (
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию ( ), средние отклонения – линейное (
), средние отклонения – линейное (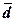 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
3. На основе рассчитанных
показателей в предположении, что распределения единиц по обоим признакам близки
к нормальному, оценить:
а) степень колеблемости значений признаков в
совокупности;
б) степень
однородности совокупности по изучаемым признакам;
в)
устойчивость индивидуальных значений признаков;
г) количество
попаданий индивидуальных значений признаков в диапазоны (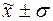 ), (
), (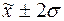 ), (
), (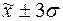 ).
).
4. Дать сравнительную
характеристику распределений единиц совокупности по двум изучаемым признакам на
основе анализа:
а) вариации
признаков;
б)
количественной однородности единиц;
в) надежности
(типичности) средних значений признаков;
г) симметричности
распределений в центральной части ряда.
5. Построить интервальный
вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных
производственных фондов и установить характер (тип) этого распределения.
Рассчитать моду Мо полученного
интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Статистический анализ генеральной
совокупности
1.
Рассчитать генеральную дисперсию 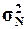 , генеральное среднее
квадратическое отклонение
, генеральное среднее
квадратическое отклонение 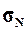 и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
2.
Для изучаемых признаков рассчитать:
а) среднюю ошибку выборки;
б) предельные ошибки выборки
для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут
находиться средние значения признака генеральной совокупности при заданных
уровнях надежности.
3.
Рассчитать коэффициенты асимметрии As
и эксцесса Ek. На основе полученных
оценок сделать вывод о степени близости
распределения единиц генеральной совокупности к нормальному распределению.
Анализ
выборочной совокупности
Задача 1. Любая исследуемая
совокупность может содержать единицы наблюдения, значения признаков которых
резко выделяются из основной массы значения. Такие нетипичные значения
признаков (выбросы) могут быть обусловлены воздействием каких-либо сугубо
случайных обстоятельств, возникать в результате ошибок наблюдения или же быть
объективно присущими наблюдаемому явлению. В любом случае они являются аномальными для совокупности, так как
нарушают статистическую закономерность изучаемого явления. Выявление аномальных
значений признака наиболее удобно производить графическим методом, используя
точечный график (диаграмму рассеяния). По расположению точек легко выявить
значения признака, которые резко выделяются из общей, однородной массы значений
признаков единиц совокупности. 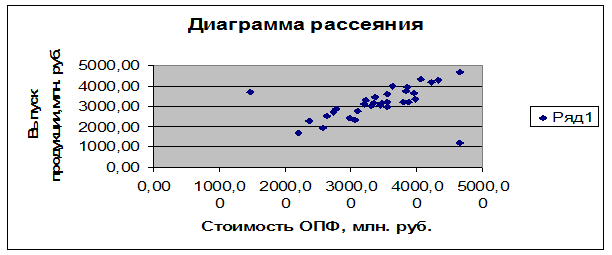
Рисунок 1 Диаграмма
рассеяния
Среди исходных данных
выявили наличие двух аномальных единиц наблюдения см. таблицу 2. На рисунке 1 они резко выделяются. Первая аномальная точка с координатами (1460,00; 3675,00)
означает, что выбранная аномальная точка
соответствует предприятию 12, которое имеет среднегодовую стоимость основных
производственных фондов, равную 1460,00 млн. руб., и выпуск продукции, равный
3675,00 млн. руб. (таблица 2) . Вторая точка с координатами (4645,00;1225,00)
предприятия 31.
Таблица
2 -Аномальные единицы наблюдения
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Выпуск
продукции, млн. руб.
|
|
12
|
1460,00
|
3675,00
|
|
31
|
4645,00
|
1225,00
|
В последствии предприятие 12 и 31 исключаются, чтобы
не привести к серьезным ошибкам в выводах о статистических свойствах совокупности.
Задача 2. Описательная статистика является инструментом статистического описания
данных, представляющих всю наблюдаемую совокупность в целом. Среди обобщающих статистических показателей наиболее часто
используются показатели центра распределения:
-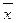 , Мо и
Ме.
, Мо и
Ме.
Средняя является обобщающей характеристикой совокупности единиц по
качественно однородному признаку. Средняя арифметическая простая равна сумме
значений признака, деленной на их число:
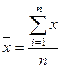 (1)
(1)
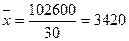 - средняя для признака
стоимости основных фондов;
- средняя для признака
стоимости основных фондов;
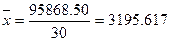 - средняя для признака выпуска продукции (таблица 3).
- средняя для признака выпуска продукции (таблица 3).
Таблица 3 - Описательная статистики
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Среднее
|
3420
|
Среднее
|
3195,616667
|
|
Стандартная
ошибка
|
108,1922592
|
Стандартная
ошибка
|
129,064075
|
|
Медиана
|
3456,75
|
Медиана
|
3172,75
|
|
Мода
|
3542,5
|
Мода
|
3185
|
|
Стандартное
отклонение
|
592,5934
|
Стандартное
отклонение
|
706,9130523
|
|
Дисперсия
выборки
|
351166,9482
|
Дисперсия
выборки
|
499726,0635
|
|
Эксцесс
|
-0,3449
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,1525
|
Асимметричность
|
0,042954448
|
|
Интервал
|
2450
|
Интервал
|
2940
|
|
Минимум
|
2195
|
Минимум
|
1715
|
|
Максимум
|
4645
|
Максимум
|
4655
|
|
Сумма
|
102600
|
Сумма
|
95868,50
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95.4%)
|
225,5605167
|
Уровень
надежности(95.4%)
|
269,0743281
|
Мода –
наиболее часто встречающееся значение признака у единиц совокупности. Оно
соответствует определенному значению признака. Таким образом, по признаку
стоимости ОПФ наиболее часто встречается размер стоимости равный
3542,5 млн.руб., а в выпуске продукции
– 3185 млн.руб.
Медиана – значение признака, которое делит единицы
ранжированного ряда на 2 части. Она лежит в середине ранжированного ряда и
делит его пополам со значениями признака
больше медианы и со значением признака меньше медианы.
Для того чтобы рассчитать медиану, нужно расположить индивидуальные значения
признака в возрастающем порядке. Затем определяют порядковый номер медианы по
формуле:
№Ме = 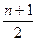 (2)
(2)
В нашем случае №Ме = 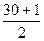 = 15,5. Это означает, что медиана расположена между 15 и 16
значениями признака в ранжированном ряду, так как ряд имеет четное число
индивидуальных значений. Таким образом, Ме
равна средней арифметической из соседних значений:
= 15,5. Это означает, что медиана расположена между 15 и 16
значениями признака в ранжированном ряду, так как ряд имеет четное число
индивидуальных значений. Таким образом, Ме
равна средней арифметической из соседних значений:
Ме1 = (3444,5+3469)/2=
3456,75 млн. руб. – медиана для признака стоимости ОПФ, т.е. 15 предприятий
имеют показатель стоимости ОПФ меньше 3456,75 млн. руб., а все остальные 15
предприятий – больше 3456,75 млн. руб.
Ме2= (3160,5+3185)/2= 3172,75 млн. руб. – медиана для признака выпуск
продукции. Это говорит о том, что 15 предприятий выпускают продукции меньше
3172,75 млн. руб., а все остальные – больше 3172,75 млн. руб.
Для установления предельного
значения амплитуды колебаний признака рассчитывают размах вариации:
R= x max – x min (3)
Значит размах
вариации стоимости ОПФ составляет : 4645-2195=2450 млн.руб. Размах по выпуску
продукции равен 4655-1715=2940 млн.руб., что на 490 млн.руб. больше чем размах
стоимости ОПФ.
Среднее линейное отклонение, вычисляется как среднее арифметическое из абсолютных
отклонений:
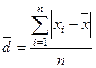 (4).
(4).
В данном примере
средняя величина колеблемости стоимости ОПФ составляет 468,76667 млн.руб. , а
для выпуска продукции 535,40667 млн.руб.
Таблица 5 - Выборочные показатели
вариации и асимметрии
Выборочные показатели
вариации и асимметрии
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн. руб."
|
|
Стандартное
отклонение
|
582,6331464
|
Стандартное
отклонение
|
695,0313144
|
|
Дисперсия
|
339461,3833
|
Дисперсия
|
483068,5281
|
|
Среднее
линейное отклонение
|
468,7666667
|
Среднее
линейное отклонение
|
535,4066676
|
|
Коэффициент
вариации, %
|
17,03605691
|
Коэффициент
вариации, %
|
21,74952089
|
|
Коэффициент
асимметрии
|
-0,21025237
|
Коэффициент
асимметрии
|
0,015275091
|
Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений
признака от их средней арифметической. Эта величина очень чутко реагирует на
вариацию признака (за счет возведения отклонений в квадрат) и органически
вписывается в аппарат математической статистики. На расчете дисперсии основаны
многие статистические показатели.
Дисперсия рассчитывается по
формуле:
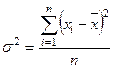 (5)
(5)
Дисперсия
признака стоимости ОПФ равная
339461,3833 означает средний квадрат
отклонение цены основных
производственных фондов от средней (3420), для выпуска продукция дисперсия
составит 483068,5281 от средней (3195).
Среднее квадратическое отклонение
показывает, на сколько в среднем отклоняется индивидуальные значения признака x i от
их средней величины 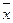 .
.
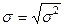 (6)
(6)
В нашем примере,
среднее квадратическое отклонение признака стоимости ОПФ составляет: 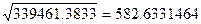 т.е. на 582,6331464 в
среднем отклоняется стоимость ОПФ от средней величины, а отклонение выпуска продукции на 695,0313144 от средней величины.
т.е. на 582,6331464 в
среднем отклоняется стоимость ОПФ от средней величины, а отклонение выпуска продукции на 695,0313144 от средней величины.
Интенсивность
вариации обычно измеряют коэффициентом
вариации, который выражается в процентах и вычисляется по формуле:
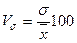 (7)
(7)
Получается, что
колебания вариантов по признаку стоимости ОПФ составляет (582,6331464/3420)* 100=17,03605691 % , а по
выпуску продукции – 21,74952089 %.
Таблица 8–Описательные статистики выборочной
совокупности.
|
|
По столбцу "Среднегодовая стоимость
основных производственных
фондов, млн.руб."
|
По столбцу
"Выпуск продукции, млн. руб."
|
|
среднее
арифметическое
|
3420
|
3195,616667
|
|
мода
|
3542,5
|
3185
|
|
медиана
|
3456,75
|
3172,75
|
|
размах
вариации
|
2450
|
2940
|
|
среднее
линейное отклонение
|
468,7666667
|
535,4066667
|
|
дисперсия
|
339461,3833
|
483068,5281
|
|
среднее
квадратическое отклонение
|
582,6331464
|
695,0313144
|
|
коэффициент
вариации, в %
|
17,03605691
|
21,74952089
|
|
коэффициент
асимметрии
|
-0,21025237
|
0,015275091
|
Для
оценки асимметричности распределения служит коэффициент Пирсона:
Asп =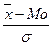 (8)
(8)
Так коэффициент асимметричности
для стоимости ОПФ составляет:
3420-3542,5/582,6331=
-0,21025237 . Для выпуска продукции коэффициент К.Пирсона равен
3195,6167-3185/695,0313= 0,015275091.
Рассчитанные выборочные показатели, представленные в
двух таблицах 3 и 5, необходимо сформировать в единую таблицу значений
выборочных показателей с заголовком «Описательные статистики выборочной
совокупности».
Задача 3.
а) Степень колеблемости признака определяется по
значению коэффициента вариации Vσ, исходя из оценочной шкалы:
0% < Vσ
≤ 40% - колеблемость незначительная;
40%
< Vσ ≤ 60% -
колеблемость средняя (умеренная);
Vσ > 60% -
колеблемость значительная.
Коэффициент вариации Vσ часто
используется для сравнения колеблемости признаков в различных рядах
распределения, когда сравнивается вариация разных признаков в одной и той же
совокупности или же вариации одного и того же признака в различных
совокупностях, имеющих разные средние х.
Итак, мы имеем вариацию Vσ1 ≈ 17%, рассчитанную по признаку «Среднегодовая стоимость основных
производственных фондов, млн. руб.» и вариацию Vσ2 ≈ 22%, рассчитанную по признаку «Выпуск
продукции, млн. руб.».
Так как 0% ≥ Vσ1 ≈ 17% ≤ 40% и 0% ≥ Vσ2
≈ 22% ≤
40%, то колеблемость этих двух признаков незначительная, отклонение
значений признаков от их средней величины небольшое.
б) Для нормальных и близких к нормальному
распределений показатель Vσ
служит индикатором однородности совокупности: принято считать, что при
выполнимости неравенства:
Vσ ≤
33% (9)
совокупность
является количественно однородной по данному признаку. Чем однороднее изучаемая
совокупность, тем надежнее полученная средняя х.
Мы предположили, что распределение единиц по обоим
признакам близки к нормальному, значит Vσ1 ≤ 33% и Vσ2 ≤
33%, то совокупность является
количественно однородной по данным двум признакам.
в) Сопоставление
средних отклонений - квадратического σn и линейного 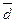 позволяет сделать вывод об устойчивости индивидуальных
значений признака, то есть об отсутствии среди них «аномальных» вариантов
значений.
позволяет сделать вывод об устойчивости индивидуальных
значений признака, то есть об отсутствии среди них «аномальных» вариантов
значений.
В условиях симметричного и нормального, а также близких
к ним распределений между показателями σn и 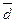 имеют место равенства
имеют место равенства
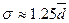
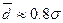
поэтому
отношение показателей σn
и 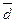 может служить индикатором устойчивости данных: если
может служить индикатором устойчивости данных: если
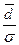 >0,8 (10)
>0,8 (10)
то
значения признака неустойчивы, в них имеются «аномальные» выбросы. Следовательно,
несмотря на визуальное обнаружение и исключение нетипичных единиц наблюдения
при выполнении Задания 1, некоторые аномалии в первичных данных сохраняться. В
этом случае их следует выявить ( например, путем поиска значений, выходящих за
границы (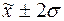 )) и рассматривать в качестве
возможных «кандидатов» на исключение из выборки.
)) и рассматривать в качестве
возможных «кандидатов» на исключение из выборки.
В нашей задаче σn1= 582,6331и d1= 468,7667 – это индивидуальные значения признака «Среднегодовая
стоимость основных производственных фондов, млн. руб.»:
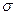 1≈1,25*468,7667=585,9583;
1≈1,25*468,7667=585,9583; 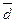 1≈0,8*582,6331=466,1065
1≈0,8*582,6331=466,1065 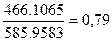 , значит значения
признака устойчивы, в них нет «аномальных» выбросов.
, значит значения
признака устойчивы, в них нет «аномальных» выбросов.
σn2= 695,0313 и d2= 535,4067 – это индивидуальные значения признака
««Выпуск продукции, млн. руб.»:
d2/ σn 2 = 0, 7567 ≈ 0, 76 значит
значения признака устойчивы, в них нет «аномальных» выбросов.
г) Сформируем
таблицу, чтобы более детально описать рассеяния признаков относительно средней
арифметической, основываясь на данных таблицы 3,5:
Таблица 9 Распределение
значений признака по диапазонам рассеяния признака относительно 
|
|
Граница
диапазона
|
Количество
значений x i, находящихся в
диапазоне
|
|
|
Первый
признак
|
Второй
признак
|
Первый
признак
|
Второй
признак
|
|
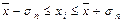
|
от 2837
до 4003
|
от 2501
до 3891
|
20- 66,7%
|
19-63,3%
|
|
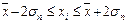
|
от 2254
до 4586
|
от 1806
до 4586
|
28-93,4%
|
28-93,4%
|
|
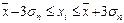
|
от 1671
до 5169
|
от 1111
до 5281
|
30-100%
|
30- 100%
|
Основываясь на
данных таблицы 9 определим процентное
соотношение рассеяния значения для первого признака : 66,7% 93,4% 100%, а для
второго признака 63,3% 93,4% 100%. В нормальном распределении и близких к ним вероятностные
оценки диапазонов рассеяния значений признаков по правилу «трех сигм» таковы (
68,3% 95,4 % 99,7%). Различие между процентами первого признака с правилом
«трех сигм» составляет 66,7<68,3,
93,4<95,4, 100>99,7 , в случаи со
вторым признаком 63,3<68,3, 93,4<95,4,
100,0>99,7.
Различие в
процентах показывает, что расстояние значений первого признака от средней
арифметической меньше, т.е. значений признака в двух диапазонах меньше, а в
третьем больше. Для второго признака в третьем диапазоне попадает значении
признака больше, а в двух остальных меньше, значит, расстояние в этих
диапазонах между средней арифметической
и значениями тоже меньше.
Задача 4. Дадим
сравнительную характеристику распределений единиц совокупности по двум
изучаемым признакам на основе анализа:
а) вариации ряда. В статистической
практике для оценки вариации ряда наиболее широко применяются показатели
размаха вариации, дисперсии, среднее квадратическое отклонение, среднее
линейное отклонение.
В нашем примере размах вариации
стоимости ОПФ составляет 2450 млн. руб., а выпуска продукции 2940 млн. руб.,
что на 490 млн. руб. больше , чем размах вариации стоимости ОПФ. Из этого
следует, что размах вариации может служить базой расчета возможных резервов
роста выборки. Таких резервов больше у признака
выпуска продукции.
Среднее линейное отклонение стоимости
ОПФ равно ≈ 468,7667, а выпуска продукции ≈ 535,4067. Это
свидетельствует о том, что отклонение признака от средней больше у выпуска
продукции.
Дисперсия стоимости ОПФ меньше, чем дисперсия у выпуска продукции на
143607,15 млн. руб.
Среднее квадратическое отклонение стоимости ОПФ составляет 582,6331
млн. руб., а у выпуска продукции 695,0313 млн. руб. Это означает, что
отклонение индивидуальных значений признака выпуска продукции от средней
величины больше на 112,3982 млн.руб. , чем отклонения значений признака
стоимости ОПФ
Вывод: отклонения признака выпуска продукции от его
средней сильнее , чем у признака стоимости ОПФ.
б) количественной однородности единиц.
Соотношение между средней, модой и медианой характеризует
форму распределения. В нормальном распределении все три характеристики верны Мо = Ме =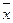 .
.
В
данном случае, для показателей признака стоимости ОПФ справедливо Мо >
Ме >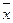 т.е. 3542,5>3456,75>3420
, если представить виде кривой то ее
вершина будет сдвинута вправо и левая часть окажется длиннее правой, то
асимметрия левосторонняя, что означает преимущественно появления в распределении
более низких значений. Для выпуска продукции
3172,75<3185<3195,62 Ме<
Мо<
т.е. 3542,5>3456,75>3420
, если представить виде кривой то ее
вершина будет сдвинута вправо и левая часть окажется длиннее правой, то
асимметрия левосторонняя, что означает преимущественно появления в распределении
более низких значений. Для выпуска продукции
3172,75<3185<3195,62 Ме<
Мо<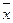 если и это представить виде кривой, то вершина кривой сдвинута влево и правая часть оказывается длиннее левой , то
асимметрия правосторонняя. Значит, что в распределении чаще встречаются более
высокие значения признака.
если и это представить виде кривой, то вершина кривой сдвинута влево и правая часть оказывается длиннее левой , то
асимметрия правосторонняя. Значит, что в распределении чаще встречаются более
высокие значения признака.
г) симметричности
распределений в центральной части ряда
Нормальное распределение является симметричным, и для
него выполняются соотношения:
Мо = Ме =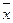 , As=0, Asп=0;
, As=0, Asп=0;
Нарушение этих соотношений свидетельствует о наличии
асимметрии распределению. Распределение с небольшой или умеренной асимметрией в
большинстве случаев по своему типу относится к нормальному.
В нормальном и
близких к нему распределениях основная масса единиц ( почти 70%) располагается
в центральной зоне ряда, в диапазоне (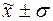 ). Для оценки асимметричности
распределения находят коэффициент К.Пирсона (см.формулу 8). Так
коэффициент асимметричности для стоимости ОПФ составляет -0,21025237– это
доказывает, что асимметрия левосторонняя АsП < 0 и для выпуска продукции коэффициент К.Пирсона равен 0,015215091–
это доказывает, что асимметричность
правосторонняя т.к АsП > 0. Более
точный показателем асимметрии распределения значений является
коэффициент асимметрии Аs:
). Для оценки асимметричности
распределения находят коэффициент К.Пирсона (см.формулу 8). Так
коэффициент асимметричности для стоимости ОПФ составляет -0,21025237– это
доказывает, что асимметрия левосторонняя АsП < 0 и для выпуска продукции коэффициент К.Пирсона равен 0,015215091–
это доказывает, что асимметричность
правосторонняя т.к АsП > 0. Более
точный показателем асимметрии распределения значений является
коэффициент асимметрии Аs:
Аs=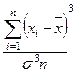 (11)
(11)
Коэффициент асимметрии для признака стоимости
ОПФ составляет -858984761/5944658610= -0,1445, для признака выпуска продукции
410715339/10071071250=0,0408. Чем больше |As|, тем более асимметрично распределение. Установлена
следующая оценочная шкала
асимметричности:
|As| ≤ 0.25 –асимметрия незначительная;
0.25<|As|≤ 0.5 –асимметрия заметная;
|As|>0.5 –асимметрия существенная. (12)
Основываясь
на этом условии, следует, что
асимметрия незначительна для первого признак и для второго.
Для оценки расхождений в степени крутизны
кривых применяется коэффициент эксцесса Ek. Как привило, Ek вычисляется только для симметричных или
близких к ним распределений по формуле:
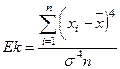 -3 (13)
-3 (13)
Для признака стоимости ОПФ Ek=
-0,4725<0, следовательно, вершина кривой распределения лежит ниже вершины
нормальной кривой, а форма кривой более пологая по сравнению с нормальной. Для
признака выпуск продукции Ek=0,3263 >0 – вершина кривой распределения
располагается выше вершины нормальной кривой, а форма кривой является более
островершинной, чем нормальная.
в) надежности
(типичных) средних значений признаков.
Для оценки надежности средней величины 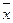 можно воспользоваться
значениями показателя вариации Vσ,
рассчитанного в таблице 5. В том и другом расчете коэффициент вариации входит в
рамки от 0 до 40% по оценочной школе
колеблемости, следовательно, его значение невелико. Индивидуальные значения признака мало отличаются друг от
друга, единицы наблюдения количественно однородны и поэтому, средняя
арифметическая величина является надежной характеристикой данной совокупности.
можно воспользоваться
значениями показателя вариации Vσ,
рассчитанного в таблице 5. В том и другом расчете коэффициент вариации входит в
рамки от 0 до 40% по оценочной школе
колеблемости, следовательно, его значение невелико. Индивидуальные значения признака мало отличаются друг от
друга, единицы наблюдения количественно однородны и поэтому, средняя
арифметическая величина является надежной характеристикой данной совокупности.
Задача 5. Используя
данные таблицы 1, построим интервальный вариационный ряд по признаку среднегодовая
стоимость основных производственных фондов. Для этого найдем сначала ширину
интервала h:
 h =
h =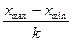 (14), где k- это
количество интервалов;
(14), где k- это
количество интервалов;
Ширина интервала
для признака стоимости ОПФ составляет h=4645-2195/5=490 ,
получается 2195-2685 ,2685-3175, 3175-3665, 3665-4155, 4155-4645.
Построение ряда
распределения завершается подсчетом численности единиц в каждой группе –
частоты групп. Иногда распределение характеризуют с помощью накопленных частот
или же используют частости и накопленные частости. Частости обычно применяются
для небольших по объему совокупностей. Кроме того, они позволяют сравнивать
распределения по одному и тому же признаку в разных по численности
совокупностях.
Полученные данные
представлены в таблице 7а:
Таблица 7а - Распределение предприятий по стоимости
основных производственных фондов
|
Группы
предприятий по среднегодовой стоимости основных фондов, млн. руб.
|
Число предприятий
в группе
|
Накопленная
частость
группы.%
|
|
Ед.
|
В % к итогу
|
|
2195-2685
|
4
|
13,3%
|
13,33%
|
|
2685-3175
|
5
|
16,7%
|
30,00%
|
|
3175-3665
|
11
|
36,7%
|
66,67%
|
|
3665-4155
|
7
|
23,3%
|
90,00%
|
|
4155-4645
|
3
|
10,0%
|
100,00%
|
|
Итого
|
30
|
100,0%
|
|
Для наглядного
представления интервальных рядов распределения используют графическое
изображение в виде гистограммы и кумуляты:
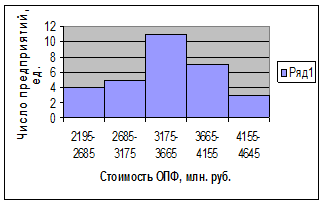
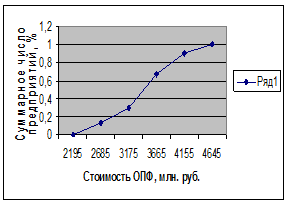
Рисунок 2.Гистограмма и кумулята
интервальный ряда.
Коэффициенты асимметричности для признака стоимости
ОПФ характеризуют левостороннюю и слабо
развитую асимметричность распределения.
По форме
гистограммы можно установить и характер закономерности распределения.
Гистограмма имеет одновершинную форму, есть основание предполагать, что выборка
является однородной по данному признаку, распределение эмпирических данных
близко к нормальному (наблюдается незначительная асимметрия).
Наибольшая частота соответствует также интервалу, то
есть мода находиться в этом интервале. Ее величина определяется по формуле:
Мо=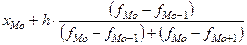 (15) где
(15) где
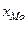 - начало модального интервала;
- начало модального интервала;
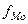 - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу;
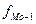 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
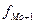 - частота интервала, следующего за модальным;
- частота интервала, следующего за модальным;
Получается, что
для признака стоимости ОПФ Мо= 3175+490*(11-5/(11-5)*(11-7)) = 3469. Нам
необходимо сравнить ее с показателем Мо несгруппированного ряда данных (см. таблицу 3). Итак, 3542.5>3469, поэтому мода
несгруппированного ряда данных больше на 73.5.
Анализ генеральной совокупности
Задача 1. Генеральные показатели 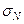 ,
, 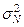 , As, Ek рассчитаны с помощью инструмента Описательная статистика, и их значения приведены в таблице 3.
, As, Ek рассчитаны с помощью инструмента Описательная статистика, и их значения приведены в таблице 3.
Дисперсию генеральной совокупности может быть оценена
непосредственно по выборочной дисперсии  .
В математической статистике доказано, что при малом числе наблюдений (особенно при n ≤40-
.
В математической статистике доказано, что при малом числе наблюдений (особенно при n ≤40-
50) для вычисления генеральной дисперсии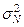 по выборочной дисперсии
по выборочной дисперсии 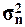 следует использовать формулу:
следует использовать формулу:
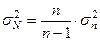 (16)
(16)
Получим, что для признака стоимости ОПФ дисперсия
равнв 351166,9482 , что на 11705,5649
больше дисперсии выборочной совокупности этого же признака, дисперсия признака выпуск продукции составляет 499
726,0636, что на 16657,5355 больше чем дисперсия признака выпуска продукции в
выборочной совокупности.
Среднее
стандартное отклонение рассчитывается
по формуле :
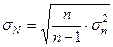 (17)
(17)
В отличии от дисперсии среднее квадратическое
отклонение является абсолютной величиной и выражается в единицах измерения
варьирующего признака.
Отклонение для
первого признака составит 592,5934 млн. руб.
это на 9,9603 млн. руб. больше, чем в выборочной совокупности , для
второго признака 706,9131
млн. руб., что на 11,8817 млн. руб. больше , чем
отклонение второго признака в выборочной совокупности.
Для нормального распределения справедливо равенство:
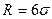 (18)
(18)
В условиях близости распределения единиц генеральной
совокупности к нормальному это соотношение используется для прогнозной
оценки размаха
вариации
признака в генеральной совокупности.
Для стоимости ОПФ размах вариации в генеральной
совокупности составит 3495,7986 , что на
1045,7986 больше размаха вариации признака в выборочной совокупности, а для второго признака 4170,1878, что на
3475,1565 больше в выборочной
совокупности.
Коэффициент асимметричности рассчитывается по формуле
(3). Для стоимости ОПФ он составит -0,1525. Для выпуска продукции коэффициент
асимметричности равен 0,0430.
Значение коэффициента эксцесса также рассчитано в
таблице 3.
Найдя значения показателей генеральной совокупности,
можно сделать вывод, что отклонение от средней в генеральной совокупности
больше, чем отклонение от средней в выборочной совокупности.
Необходимо сформировать для показателей генеральной совокупности отдельную таблицу с заголовком «Описательные статистики генеральной совокупности»:
Таблица № 10 Описательная
статистика генеральной совокупности
|
|
стоимость ОПФ
|
выпуск
продукции
|
|
дисперсия
|
351166,9482
|
499726,0636
|
|
среднее
стандартное отклонение
|
592,5934
|
706,9131
|
|
размах
вариации
|
3495,7986
|
4170,1878
|
|
коэффициент
асимметричности
|
-0,1525
|
0,0430
|
|
коэффициент
эксцесса
|
-0,3449
|
-0,2053
|
Задание 2.
Для изучаемых признаков нужно рассчитать:
а) среднюю
ошибку выборки, которая рассчитана и
приведена в таблице 3 (параметр Стандартная
ошибка). Для ответа на этот вопрос следует выбрать ее из этой таблицы.
Достоверность генеральных параметров зависит от репрезентативности
выборки, т.е. от того, насколько полно и адекватно представлены в выборке
статистические свойства генеральной совокупности. Для среднего значения средняя
ошибка выборки выражает среднее квадратическое отклонение выборочной средней от математического
ожидания генеральной средней. Величина средней ошибки выборки зависит от объема
выборки n и от величины вариации признака σ: чем больше n и меньше σ, тем меньше
ошибка. Средняя ошибка выборки может быть определена по формуле:
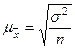 (19)
(19)
Итак, средняя ошибка выборки для признака стоимость
ОПФ равна 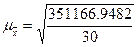 ≈ 108,1923, для признака выпуск продукции
≈ 108,1923, для признака выпуск продукции  ≈ 129,0641.
≈ 129,0641.
б) предельную ошибку выборки. Оценки предельных ошибок выборки имеются в таблице 3,
4а, 4б. На основе этих оценок и формулы (21) необходимо сформировать таблицу 11.
Предельная
ошибка выборки определяет границы, в пределах которых лежит генеральная средняя
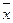 . В математической статистике доказано, что предельная ошибка
выборки, кратна средней ошибке с коэффициентом кратности t, зависящим от значения доверительной вероятности P:
. В математической статистике доказано, что предельная ошибка
выборки, кратна средней ошибке с коэффициентом кратности t, зависящим от значения доверительной вероятности P:
 (20)
(20)
Величина
коэффициента t (называемого также коэффициентом
доверия) является нормированным отклонением, его значения подсчитаны для
различных уровней надежности P и
протабулированы (хранятся в таблицах интегральной функции Лапласа).
Предельная ошибка выборки позволяет определить предельные значения показателей генеральной
совокупности и их доверительные интервалы. Для генеральной средней
предельные значения и доверительный интервалы определяются выражениями:
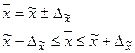 (21)
(21)
Таблица 11 –Предельные
ошибки выборки и ожидаемые границы для генеральной средней
|
Доверительная
вероятность
|
Коэффициент
доверия
|
Предельные ошибки
выборки
|
Ожидаемые границы для средних
|
|
Для первого признака
|
Для
второго признака
|
Для первого признака
|
Для второго признака
|
|
0,683
|
1
|
110,1619
|
131,4137
|
3309,8381≤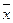 ≤3530,1619 ≤3530,1619
|
3066,203≤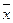 ≤3329,0304 ≤3329,0304
|
|
0,954
|
2
|
225,5605
|
269,0743
|
3194,4394≤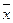 ≤3645,5605 ≤3645,5605
|
2928,5424≤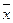 ≤3466,691 ≤3466,691
|
|
0,997
|
3
|
350,4782
|
418,0904
|
3770,4782≤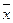 ≤3770,4782 ≤3770,4782
|
2779,5263≤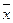 ≤3615,7071 ≤3615,7071
|
Задача 3. Если распределение единиц выборочной совокупности
близко к нормальному, выборка является репрезентативной (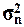 и
и 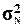 значения показателей расходятся
незначительно) и при этом коэффициенты AsN, EkN,
указывают на небольшую или умеренную величину
асимметрии и эксцесса соответственно, то есть основание полагать, что
распределение единиц генеральной совокупности по изучаемому признаку будет
близко к нормальному.
значения показателей расходятся
незначительно) и при этом коэффициенты AsN, EkN,
указывают на небольшую или умеренную величину
асимметрии и эксцесса соответственно, то есть основание полагать, что
распределение единиц генеральной совокупности по изучаемому признаку будет
близко к нормальному.
Значения коэффициентов асимметрии As и эксцесса Ek
имеются в таблице 10. Получим, что для первого признака коэффициент
асимметрии равен-0,1525, для
второго признака 0,0430. На основе
оценочной шкалы асимметричности, можно сделать вывод, что асимметрия
незначительная как для первого признака,
так и для второго.
Показатель эксцесса для первого признака -0,3449
меньше нуля, тогда вершина кривой распределения лежит ниже вершины нормальной
кривой, а форма более пологая по сравнению с нормальной. Показатель эксцесса
для второго признака -0,2053 тоже меньше нуля, тогда вершина кривой
распределения лежит ниже вершины нормальной кривой, а форма более пологая по
сравнению с нормальной.
Лабораторная работа №2
В лабораторной работе № 2 изучается взаимосвязь между
факторным признаком Среднегодовая стоимость основных производственных фондов
(признак X) и результативным признаком
Выпуск продукции (признак Y), значениями
которых являются исходные данные Лабораторной работы № 1 после исключения из
них аномальных значений.
В процессе статистического исследования необходимо
решить ряд задач.
1. Установить
наличие статистической связи между факторным признаком X и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов;
2. Установить наличие корреляционной связи между признаками X и Y методом аналитической
группировки.
3. Оценить тесноту связи признаков X и Y на основе:
а) эмпирического корреляционного отношения 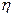 ;
;
б) линейного коэффициента корреляции r.
4. Построить однофакторную линейную регрессионную модель
связи признаков X и Y, используя инструмент Регрессия настройки Пакет
анализа.
5. Оценить адекватность и практическую пригодность
построенной линейной регрессионной модели, указав:
а) доверительный интервалы коэффициентов a0, a1 ;
;
б) степень тесноты связи признаков X и Y;
в) погрешность регрессионной модели.
6. Дать экономическую интерпретацию:
а) коэффициента регрессии а1
б)
коэффициента эластичности Kэ ;
в)
остаточных величин 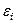 .
.
7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью
средств инструментов Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
Задание 1. В статистических исследованиях рассматривается особая
разновидность стохастических связей – статистические связи.
Стохастическую связь между случайными значениями признаков X и Y называют статистической,
если с изменением значений xi
фактора X закономерным образом изменяется какой-либо из обобщающих статистических показателей
распределения yi1, yi2, …, yik признака Y.
Наиболее удобной формой представления корреляционных
зависимостей при большом числе наблюдений являются групповые аналитические таблицы, отражающие результаты аналитической группировки совокупности по
факторному признаку. Примером аналитической таблицы в нашей работе является
таблица 2.2:
Таблица 2.2. Зависимость выпуска продукции от
среднегодовой стоимости ОПФ (аналитическая группировка)
|
Номер группы
|
Группы
предприятий по среднегодовой стоимости основных фондов, млн. руб.
|
Число
предприятий, ед.
|
Выпуск продукции,
млн. руб.
|
|
Всего
|
В среднем на
одно предприятие
|
|
1
|
2195-2685
|
4
|
8477,00
|
2119,25
|
|
2
|
2685-3175
|
5
|
13058,50
|
2611,7
|
|
3
|
3175-3665
|
11
|
35843,50
|
3258,5
|
|
4
|
3665-4155
|
7
|
25382,00
|
3626
|
|
5
|
4155-4645
|
3
|
13107,50
|
4369,166667
|
|
ИТОГО
|
|
30
|
95868,5
|
3195,616667
|
При построении аналитической таблицы для каждой
выделенной i-й группы подсчитывается
численность составляющих ее факторных значений x, а также суммарное и среднее 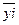 групповые значения
результативного признака.
групповые значения
результативного признака.
а) В случае
сгруппированных факторных значений для графического представления применяют
эмпирическую линию связи, называемая также эмпирической линией регрессии.
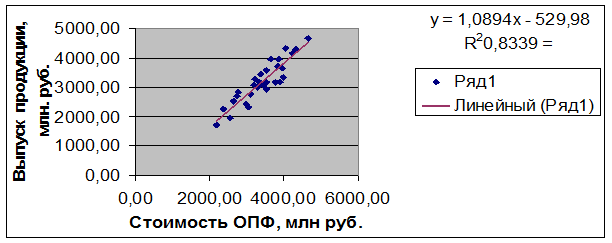
Рисунок
3 Корреляционное поле и
эмпирическая линия связи для групповых
средних 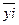 .
.
б) К элементарным статистическим методам выявления
взаимосвязей признаков относятся метод сопоставления взаимосвязанных
параллельных рядов. Метод заключается в выявлении статистической связи
признаков путем простого параллельного сравнения факторных и результативных
значений у отдельных единиц совокупности. Для этого значения х1, х2,
…,хn фактора ранжируются в порядке возрастания (или
убывания). Затем строится ряд соответствующих значений результативного признака
Y, и путем сопоставления двух построенных рядов
выявляется либо наличие (и направление) связи, либо ее отсутствие.
В данной работе ранжируем исходный данные (см. таблица
1) по признаку стоимости ОПФ. С возрастанием значений признака стоимости ОПФ
значения признака выпуска продукции также в целом возрастают при наличии
некоторых отклонений от этой общей тенденции. Следовательно, между признаками
возможно наличие прямой корреляционной связи:
Таблица 2.1 – Исходные данные
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
5
|
2195,00
|
1715,00
|
|
23
|
2366,50
|
2278,50
|
|
27
|
2562,50
|
1960,00
|
|
1
|
2636,00
|
2523,50
|
|
8
|
2734,00
|
2695,00
|
|
32
|
2783,00
|
2842,00
|
|
22
|
2979,00
|
2425,50
|
|
19
|
3052,50
|
2327,50
|
|
2
|
3101,50
|
2768,50
|
|
3
|
3199,50
|
3087,00
|
|
13
|
3224,00
|
3283,00
|
|
26
|
3297,50
|
3013,50
|
|
9
|
3346,50
|
3160,50
|
|
4
|
3371,00
|
3430,00
|
|
28
|
3444,50
|
3062,50
|
|
17
|
3469,00
|
3136,00
|
|
6
|
3542,50
|
2940,00
|
|
14
|
3542,50
|
3577,00
|
|
25
|
3542,50
|
3185,00
|
|
7
|
3640,50
|
3969,00
|
|
30
|
3787,50
|
3185,00
|
|
18
|
3836,50
|
3724,00
|
|
10
|
3861,00
|
3944,50
|
|
20
|
3885,50
|
3185,00
|
|
24
|
3959,00
|
3650,50
|
|
29
|
3983,50
|
3356,50
|
|
15
|
4057,00
|
4336,50
|
|
11
|
4228,50
|
4165,00
|
|
21
|
4326,50
|
4287,50
|
|
16
|
4645,00
|
4655,00
|
Задание 2. Если при изменении xi имеет
место закономерное изменение средних
арифметических значений 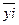 распределения признака
Y, то статистическая связь называется корреляционной.
распределения признака
Y, то статистическая связь называется корреляционной.
При выявлении наличия связи методом аналитической
группировки формируется группировка единиц совокупности по факторному признаку
Х, а затем для каждой выделенной j-й группы рассчитываются
средние значения 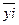 результативного
признака Y. Если при переходе от одной
группы к другой средние значения
результативного
признака Y. Если при переходе от одной
группы к другой средние значения 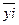 будут меняться с
определенной закономерностью – возрастать или убывать, то между признаками X и Y существует корреляционная связь.
будут меняться с
определенной закономерностью – возрастать или убывать, то между признаками X и Y существует корреляционная связь.
Как, например, в таблице 2.2 средние значения выпуска
продукции меняются с определенной закономерностью, а именно возрастают,
следовательно, между стоимостью ОПФ и выпуском продукции корреляционная связь
есть.
Задание 3. Теснота корреляционной связи
характеризует степень ее приближения к функциональной связи. Степень тесноты
связи зависит от степени варьирования результативного признака Y при фиксированном значении факторного признака Х.
При использовании метода аналитической группировки
оценивается степень тесноты корреляционной связи между признаками, для чего
рассчитывается специальный показатели :
r – линейный коэффициент корреляции;
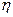 - эмпирическое корреляционное отношение;
- эмпирическое корреляционное отношение;
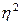 - эмпирический коэффициент детерминации.
- эмпирический коэффициент детерминации.
Расчет
показателей производится по формулам:
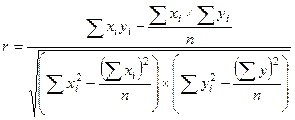 ,
, 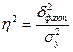 ,
, 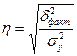 (22)
(22)
n- число единиц наблюдения;
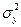 - общая дисперсия признака Y;
- общая дисперсия признака Y;
где 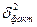 - межгрупповая дисперсия признака Y, которая определяется:
- межгрупповая дисперсия признака Y, которая определяется: 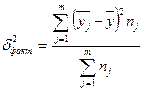 или
или 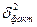 =
= 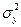 -
-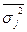 (23) , где
(23) , где 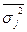 - внутригрупповая дисперсия j-й группы результативных значений j=1,2,3,4,5.
- внутригрупповая дисперсия j-й группы результативных значений j=1,2,3,4,5.
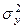 - общая дисперсия признака Y, которая вычисляется по формуле:
- общая дисперсия признака Y, которая вычисляется по формуле:
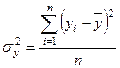 или
или 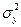 =
= 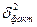 +
+ 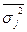 (24)
(24)
Результаты выполненных расчетов представлены в таблице
2.4. и 2.5.:
Таблица
2.4 Дисперсии и эмпирические показатели тесноты взаимосвязи
|
Общая дисперсия
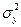
|
Средняя из
внутригрупповых дисперсий
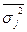
|
Межгрупповая
дисперсия
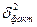
|
Эмпирический
коэффициент детерминации
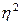
|
Эмпиричское
корреляционное отношение
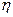
|
|
|
|
483068,5281
|
89374,55722
|
393693,9708
|
0,814985759
|
0,902765617
|
|
Таблица 2.5. Линейный коэффициент корреляции
признаков.
|
|
Столбец 1
|
Столбец 2
|
|
Стоимость
ОПФ
|
1
|
|
|
Выпуск
|
0,91318826
|
1
|
В нашем случае
общая дисперсия признака Y, обусловленная
влиянием на Y всех факторов, включая X, равна 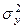 = 483068,5281. Межгрупповая дисперсия результативного признака
Y, обусловленная влиянием только фактора X -
= 483068,5281. Межгрупповая дисперсия результативного признака
Y, обусловленная влиянием только фактора X - 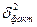 =393693,9708. Эмпирический коэффициент детерминации
(причинности), определяющий силу, то есть оценивающий, насколько вариация
результативного признака Y объясняется
вариацией фактора X, равна
=393693,9708. Эмпирический коэффициент детерминации
(причинности), определяющий силу, то есть оценивающий, насколько вариация
результативного признака Y объясняется
вариацией фактора X, равна 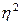 =0,8150. Эмпирическое корреляционное отношение, выступающее
как универсальный показатель тесноты связи при любой форме связи (как линейной,
так и нелинейной) -
=0,8150. Эмпирическое корреляционное отношение, выступающее
как универсальный показатель тесноты связи при любой форме связи (как линейной,
так и нелинейной) - 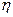 =0,9028. Линейный коэффициент корреляции, изменяющий тесноту
связи в предположении линейности взаимосвязи признаков X и Y - r=0, 9132.
=0,9028. Линейный коэффициент корреляции, изменяющий тесноту
связи в предположении линейности взаимосвязи признаков X и Y - r=0, 9132.
Для показателей силы и тесноты корреляционной связи
характерна свойство: чем ближе значение показателя (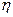 ,
,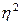 , r) к единицы
, тем теснее связь и больше сила связи. Для качественной оценки тесноты связи
используется шкала Чэддока, в которой значение показателей тесноты связи |r| и
, r) к единицы
, тем теснее связь и больше сила связи. Для качественной оценки тесноты связи
используется шкала Чэддока, в которой значение показателей тесноты связи |r| и 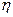 от 0,9 до 0,99
характеризует связь как весьма высокую. Знак «+» при r указывает направление связи : на прямую линейную
зависимость.
от 0,9 до 0,99
характеризует связь как весьма высокую. Знак «+» при r указывает направление связи : на прямую линейную
зависимость.
Задание 4. Простейшей формой корреляционной связи признаков
является парная линейная корреляция, представляющая собой линейную зависимость
результативного признакаY от факторного
признака X.
Уравнение
парной линейной корреляционной связи
имеет следующий вид:
 (25), где
(25), где
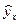 - расчетное теоретическое значение результативного признака Y, полученное по уравнению регрессии;
- расчетное теоретическое значение результативного признака Y, полученное по уравнению регрессии;
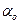 - среднее значение
признака Y в точке х=0;
- среднее значение
признака Y в точке х=0;
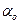 ,
, 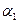 - коэффициенты
уравнения регрессии (параметры связи).
- коэффициенты
уравнения регрессии (параметры связи).
Уравнение парной линейной корреляции показывает
среднее изменение результативного признака Y при изменении фактора X на одну единицу его измерения, то есть вариацию
признака Y, которая приходится на единицу
фактора X. Знак параметра указывает направление этого
измерения.
Коэффициенты
уравнения 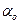 ,
, 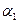 отыскиваются методом наименьших квадратов
(МНК). Критерий метода наименьших квадратов можно записать таким образом:
отыскиваются методом наименьших квадратов
(МНК). Критерий метода наименьших квадратов можно записать таким образом:
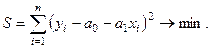 (26)
(26)
Для нахождения параметров 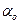 ,
, 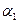 используют систему нормальных уравнений МНК:
используют систему нормальных уравнений МНК:
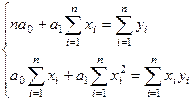 (27)
(27)
Решая полученную систему, находим параметры 
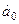 ,
,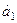 :
:
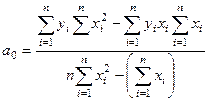 ;
; 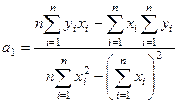 (27)
(27)
Иногда эти коэффициенты удобнее вычислять по формулам:
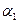 =
= 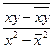 ;
; 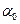 =
= 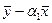 (28).
(28).
Параметры уравнения регрессии рассчитаны с помощью
инструмента Регрессия настройки Пакет анализа и равны 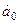 = -529,9781 и
= -529,9781 и 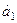 = 1,0894. Получим
= 1,0894. Получим 
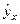 = 1,0894х-529,9781. Для большей уверенности проверим систему
нормальных уравнений МНК для линейного уравнения регрессии:
= 1,0894х-529,9781. Для большей уверенности проверим систему
нормальных уравнений МНК для линейного уравнения регрессии:

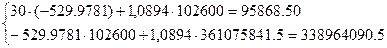 верно.
верно.
Мы получили линейное уравнение регрессии 
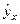 = 1,0894х-529,9781, которое показывает, что с увеличением
стоимости ОПФ на один млн. руб. в среднем выпуск продукции возрастет на 1,0894
млн. руб.
= 1,0894х-529,9781, которое показывает, что с увеличением
стоимости ОПФ на один млн. руб. в среднем выпуск продукции возрастет на 1,0894
млн. руб.
.
Задание 5. Оценим адекватность и практическую пригодность
построенной линейной регрессионной модели.
а) Рассчитаем доверительный интервалы коэффициентов a0, a1 :
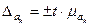 (29), где
(29), где
t-коэффициент доверия, соответствующий заданному уровню
надежности P.
Для наглядности поместим полученные результаты в
таблицу 12:
Таблица 12 – Доверительный интервал коэффициентов a0, a1
|
вероятность
параметры
|
0,95
|
0,683
|
|
нижние
|
верхние
|
нижние
|
верхние
|
|
a0
|
-1182,888488
|
122,9323832
|
-854,7247158
|
-205,2313886
|
|
a1
|
0,901157173
|
1,277553188
|
0,995748659
|
1,182961703
|
Проверим статистическую значимость параметра а k (т.е.
неслучайность найденного значения а k , его типичность для всей генеральной совокупности) путем
сопоставления величины а k со средней ошибкой 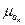 исходя из t- критерия
Стъюдента:
исходя из t- критерия
Стъюдента:
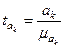 (30)
(30)
Получаем что 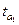 = 11,8569 > tтабл (α=0,05,
28)=2,04 , то параметр а1 считается
значимым.
= 11,8569 > tтабл (α=0,05,
28)=2,04 , то параметр а1 считается
значимым.
б) Теснота связи
признаков X и Y находится на основе следующих показателей:
индексов
детерминации R2 –показывает какая часть общей вариации расчетных
значений признака Y объясняется вариацией фактора X;
индекс корреляции
R – оценивает степень тесноты чвязи между факторными
признаками хi и расчетными результативными значениями 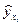 ;
;
линейный
коэффициент корреляции r, используемый для измерения тесноты связи признаков в
регрессионной модели в случае линейной функции связи;
которые определяются по следующими формулами:
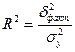 ;
; 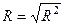 ; r=
; r=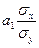 (31)
(31)
|
Таблица
2.5 Регрессионная
статистика
|
|
Множественный
R =r
|
0,91318826
|
|
R-квадрат =R^2
|
0,833912798
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
Стандартная
ошибка =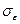
|
293,1933177
|
|
Наблюдения =n
|
30
|
Из этого следует, что линейный коэффициент корреляции и индекс корреляции
принимает значение 0,9132 близкое к единицы и, что свидетельствует о тесной
связи признаков в регрессионной модели. Индекс детерминации равный 0,8339
означает, что степень тесноты связи признаков в уравнении регрессии высокое.
При этом более 80% (83,39%) вариации расчетных значений признака Y объясняется влиянием признака X, что
позволяет считать применение синтезированного уравнения регрессии правомерным.
в) Так как
показатели тесноты связи R и r рассчитываются
на основе совокупности наблюдаемых эмпирических данных, значения которых могли
быть искажены влиянием случайных факторов, то проверим показатели тесноты связи
на их неслучайность с помощью критерия Стьюдента, фактическое значение которого
рассчитывается по формуле:
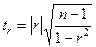 (32)
(32)
Расчетное значение критерия 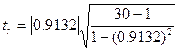 = 12,0701 сравнивается с критическим tтабл ,
определяемым по таблице значений t-Стъюдента (при
α=0,05 k=28 (n-2)) равный 2,0484 ,то
tрасч > tтабл и величина коэффициент корреляции признается значимой.
= 12,0701 сравнивается с критическим tтабл ,
определяемым по таблице значений t-Стъюдента (при
α=0,05 k=28 (n-2)) равный 2,0484 ,то
tрасч > tтабл и величина коэффициент корреляции признается значимой.
Для оценки значимости индекса корреляции R применяется F-
критерии Фишера FR, фактическое
значение которого определяется по формуле:
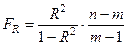 (33), где
(33), где
m- число параметров уравнения регрессии .
Так как Fрасч =
140,6851, что больше Fтабл (при
α=0,05 , k1 = 1k2 =28), то величина найденного индекса корреляции R признается значимой.
Значимость
показателей тесноты связи R и r означает , что зависимость между признаками X и Y регрессионной
модели является статистически существенна, т.е. построенная регрессионная
модель в целом адекватна исследуемому процессу. Следовательно, выводы,
сделанные на основе регрессионной модели, построенной по данным органической
выборки, можно с достаточной вероятностью распространить на всю генеральную
совокупность.
В качестве критерия адекватности регрессионной модели
используются следующие модели:
·
Средняя
квадратическая ошибка уравнения регрессии 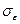 , представляющая собой среднее квадратическое отклонение
эмпирических значений признака Y от
теоретических:
, представляющая собой среднее квадратическое отклонение
эмпирических значений признака Y от
теоретических:
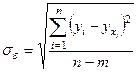 (34)
(34)
·
средняя ошибка
аппроксимации  , выраженная в процентах:
, выраженная в процентах:
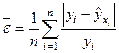 100 % (35)
100 % (35)
В адекватных моделях ошибки 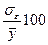 и
и  не должны превышать
12-15%. В нашей задаче получаем, что средняя ошибка аппроксимации составляет 8
%, а отношение
не должны превышать
12-15%. В нашей задаче получаем, что средняя ошибка аппроксимации составляет 8
%, а отношение 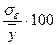 = 9 % , поэтому модель адекватна.
= 9 % , поэтому модель адекватна.
Задание 6.
а) В
процессе анализа прежде всего выясняется, как факторный признак влияет на
величину результативного признака. Чем больше величина коэффициентов регрессии 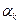 при к-й степени
фактора X, тем значительнее влияние данного признака на
результативный.
при к-й степени
фактора X, тем значительнее влияние данного признака на
результативный.
В нашем случае линейного уравнения регрессии 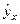 = 1,0894х-529,9781 величина коэффициента
= 1,0894х-529,9781 величина коэффициента 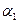 = 1,0894 показывает, что с увеличением стоимости ОПФ на один
млн. руб. в среднем выпуск продукции возрастает на 1,0894 млн. руб.
= 1,0894 показывает, что с увеличением стоимости ОПФ на один
млн. руб. в среднем выпуск продукции возрастает на 1,0894 млн. руб.
б) С целью расширения возможностей экономического анализа
используется коэффициент эластичности, который показывает, на сколько
процентов изменяется в среднем результативный признак при изменении факторного
признака на 1%.
Для определения коэффициента
эластичности используют формулу:
Кэ =
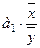 (36)
(36)
Вычислим
коэффициент эластичности для нашего задания :
Кэ=1,0894*(3420/3195,6167)=1,1659
. Это означает, что при росте стоимости ОПФ
на 1% выпуск продукции возрастет
на 1,1659%.
в) Анализируя
остатки 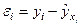 (37), характеризующие отклонения i-х наблюдений от значений
(37), характеризующие отклонения i-х наблюдений от значений 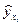 , которые следует ожидать в среднем, можно сделать ряд
практических выводов об эффективности экономической деятельности
рассматриваемых хозяйствующих субъектов и выявить скрытые резервы их развития и
повышения деловой активности. При этом наиболее значительный экономический
интерес представляют наибольшие и наименьшие положительные и отрицательные
отклонение
, которые следует ожидать в среднем, можно сделать ряд
практических выводов об эффективности экономической деятельности
рассматриваемых хозяйствующих субъектов и выявить скрытые резервы их развития и
повышения деловой активности. При этом наиболее значительный экономический
интерес представляют наибольшие и наименьшие положительные и отрицательные
отклонение 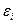 .
.
При построении регрессионной модели 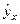 = 1,0894х-529,9781 численное значение коэффициента
= 1,0894х-529,9781 численное значение коэффициента 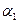 = 1,0894 выбрано так, чтобы обеспечить наименьшие возможные
остатки
= 1,0894 выбрано так, чтобы обеспечить наименьшие возможные
остатки 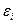 для всех случаев
наблюдения (см. таблицу 2.6.). Наименьшее положительное (отрицательное)
отклонение
для всех случаев
наблюдения (см. таблицу 2.6.). Наименьшее положительное (отрицательное)
отклонение 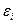 =44,95 (
=44,95 (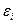 =-48,67) выявлено при 13 (12) наблюдении, что говорит о
наименьшей эффективности (не эффективности) экономической деятельности
рассматриваемого хозяйствующего субъекта. Наибольшее положительное
(отрицательное) отклонение
=-48,67) выявлено при 13 (12) наблюдении, что говорит о
наименьшей эффективности (не эффективности) экономической деятельности
рассматриваемого хозяйствующего субъекта. Наибольшее положительное
(отрицательное) отклонение 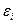 =533,18 (
=533,18 (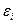 =-517,71) находится при 20 (24) наблюдении, что указывает на наивысшую
эффективность (не эффективность) экономического субъекта.
=-517,71) находится при 20 (24) наблюдении, что указывает на наивысшую
эффективность (не эффективность) экономического субъекта.
Таблица 2.6. Вывод остатков
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
1861,15657
|
-146,15657
|
|
2
|
2047,980984
|
230,5190165
|
|
3
|
2261,494599
|
-301,494599
|
|
4
|
2341,562205
|
181,9377952
|
|
5
|
2448,319013
|
246,6809875
|
|
6
|
2501,697416
|
340,3025836
|
|
7
|
2715,211032
|
-289,7110319
|
|
8
|
2795,278638
|
-467,7786377
|
|
9
|
2848,657042
|
-80,15704153
|
|
10
|
2955,413849
|
131,5861507
|
|
11
|
2982,103051
|
300,8969488
|
|
12
|
3062,170657
|
-48,670657
|
|
13
|
3115,549061
|
44,95093913
|
|
14
|
3142,238263
|
287,7617372
|
|
15
|
3222,305869
|
-159,8058686
|
|
16
|
3248,995071
|
-112,9950705
|
|
17
|
3329,062676
|
-389,0626763
|
|
18
|
3329,062676
|
247,9373237
|
|
19
|
3329,062676
|
-144,0626763
|
|
20
|
3435,819484
|
533,1805159
|
|
21
|
3595,954696
|
-410,9546957
|
|
22
|
3649,3331
|
74,66690047
|
|
23
|
3676,022301
|
268,4776985
|
|
24
|
3702,711503
|
-517,7115034
|
|
25
|
3782,779109
|
-132,2791092
|
|
26
|
3809,468311
|
-452,9683111
|
|
27
|
3889,535917
|
446,9640831
|
|
28
|
4076,36033
|
88,63966954
|
|
29
|
4183,117138
|
104,3828618
|
|
30
|
4530,076763
|
124,9232367
|
Задание 7. В случаях, когда рассматриваются альтернативные
регрессионные модели, индекс детерминации 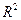 используется в
качестве критерия предпочтительности того или иного уравнения регрессии: наилучшей считается модель с наибольшим
значением
используется в
качестве критерия предпочтительности того или иного уравнения регрессии: наилучшей считается модель с наибольшим
значением 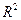 .
.
Путем визуального анализа значения R2 выбираем по максимальной величине R2 наиболее
адекватное уравнение регрессии.
В
итоге, наиболее адекватное уравнение
регрессии и его график имеет вид :
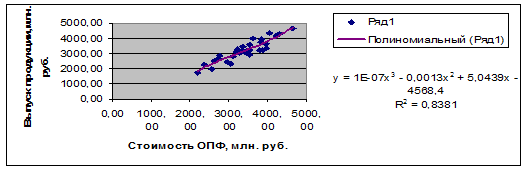
Рисунок 4. Наиболее адекватное уравнение регрессии и его
график.