Задача 1
Определить величину и
направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня
находится воздух, слева от поршня и в резервуаре, куда опущен открытый конец
трубы – масло трансформаторное. Показание пружинного манометра – 80000 Па (абс).
Дано: Н=8м, D= 120, d=60 мм.
Решение:
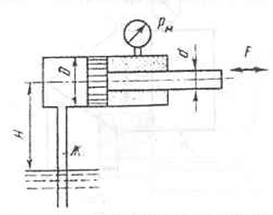
Для удержания поршня на
месте необходимо прижить силу, направленную от поршня, как показано на рисунке
жирной стрелкой. По величине эта сила должна уравновесить силу давления в 0,8
атм. со стороны жидкости. Сила давления жидкости на некоторую площадь[1]:
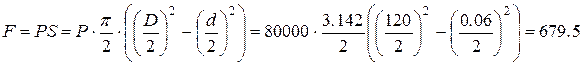Н.
Ответ: 754,08 Н;
направлена вправо от поршня.
Задача 7
При истечении жидкости из резервуара в атмосферу по
горизонтальной трубе диаметром d=50 мм и длиной l = 6 м. Уровень в пьезометре, установленном посередине трубы, равен h=3,5 м. Определить расход Q и коэффициент гидравлического трения l, если статический напор в баке постоянен и равен Н=8 м. Построить
пьезометрическую и напорную линии. Сопротивлением жидкости в труб пренебречь.
Решение:
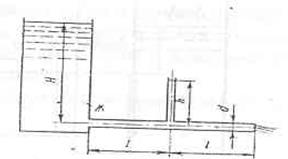
Искомый расход с учетом потерь в соединительных трубах
находится по формуле[2]
.
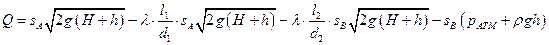Выполним элементарные преобразования с этой формулой:
.
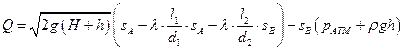Подставим числовые значения:
Для построения пьезометрических линий, найдем
пьезометрические высоты соответственно в точках А и В:
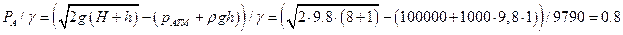м.
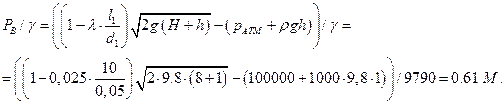
Тогда пьезометрическая линия выглядит следующим образом:
Задача 10
Определить диаметр трубопровода, по которому попадает
жидкость Ж (глицерин) с расходом Q = 4,5 л/с, из условия получения в нем максимально возможной скорости при
сохранении ламинарного режима. Температура жидкости t = 20° C.
Решение:
При температуре t = 20° C плотность глицерина 1250 кг/м3.
Формула для расхода воды в случае ламинарного течения
жидкости
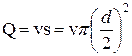, откуда диаметр трубопровода
.
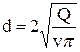Соблюдем условие максимальной (критической) скорости перехода
от ламинарного к турбклентному течению. Число Рейнольдса, соответствующее
критической скорости, равно 2320. Формула, связывающая критическое число
Рейнольдся, критическую скорость, диаметр трубы и кинематическую вязкость
жидкости, имеет вид:
.
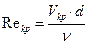Отсюда критическая скорость для воды при температуре t = 20° C:
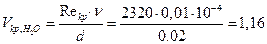м/с.
Тогда искомый диаметр трубы:
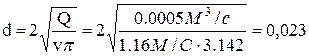м.
Ответ: 0,023 м..
Задача 22
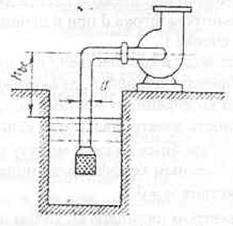
Центробежный насос
производительностью Q=62 л/с работает при частоте вращения
п=1470 об/мин. Определить допустимую высоту всасывания, если диаметр
всасывающей трубы d=200 мм, а ее длина l=5 м. Коэффициент кавитации в формуле Руднева принять
равным С=800. Температура воды t=20°С. Коэффициент сопротивления колена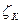 
=0,2. Коэффициент сопротивления входа в трубу 
=1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.
Решение:
Для случая центробежного
насоса и коленчатой передачи воды расход воды рассчитывается по формуле[3]:
.
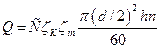Выразим из этой формулы
искомую величину (высоту) и подставим исходные данные задачи, учитывая, что 62
л/с равен 0,062 м3/с:
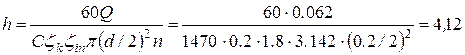м.
Ответ: 4,12 м.
Задача 28
Определить средний
объемный коэффициент полезного действия, максимальную теоретическую подачу и
степень неравномерности подачи поршневого насоса двойного действия и диаметром
цилиндра D = 100 мм, ходом поршня S = 60 мм, диаметром штока d = 25 мм, при n = 60 (об/мин) двойных ходах в
минуту, заполняющего мерный бак W = 0.077 м3 за
t = 100 с.
Решение:
Действительная
производительность насоса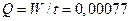 
м3/сек. Максимальная
теоретическая производительность насоса двойного действия будет
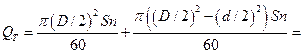
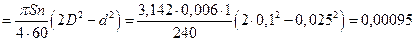м3/сек.
Отношение
действительной подачи Q к
теоретической QT
называется объемным КПД поршневого насоса:
.
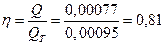Степень неравномерности
подачи насоса можно принять для одноцилиндрового – 3,14, а для двухцилиндрового
– 1,57.
Задача 31
Силовой гидравлияеский
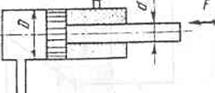
цилиндр нагружен силой F=60000 Н и делает п=11 об/мин двойных ходов в минуту.
Длина хода поршня S=100 см, диаметр поршня D=120 мм, диаметр штока d=40 мм. Определить давление масла,
потребную подачу и среднюю скорость поршня. Механический коэффициент полезного
действия гидроцилиндра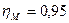 
, объемный коэффициент полезного действия 
.
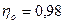Решение:
Давление масла:
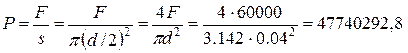Па.
Поршневой насос, совершающий
двойные ходы, обеспечивает подачу жидкости
Q=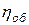
∙
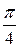∙D2∙S∙2n = 0.98∙
м3/с.
Скорость поршня с учетом
механических потерь определим следующим образом. Совершая двойные ходы, поршень
проходит в минуту:
V = 2nS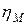
= 2∙11 об/мин
∙100 см ∙ 0.95 = 2090 см/мин = 0.35 м/c.
Ответ: P = 47,7 Мпа; Q = 0.008 м3/c; V = 0.35 м/c.
Список литературы
1.
Башта
Т.М., Руднев С.С. Гидравлика, гидромашины и гидропривод. – М.: Машиностроение,
1982.
2.
Дергачев
Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
3.
Задачник
по гидравлике, гидромашинам и гидроприводу / под ред. Б.Б. Некрасова. – М.:
Высшая школа, 1989.
4.
Осипов
П.Е. Гидравлика, гидромашины и гидропривод. – М.: Лесная промышленность, 1981.
5.
Юфин
А.П. Гидравлика, гидромашины и гидропривод. – М.:
[1] Осипов П.Е. Гидравлика, гидромашины и гидропривод. – М.: Лесная
промышленность, 1981. – с. 11.
[2] Дергачев Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
– с. 82.
[3] Дергачев Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
– с. 109.