Министерство
образования и науки Российской Федерации
Федеральное
агентство по образованию
Государственное образовательное учреждение
высшего профессионального
образования
Контрольная
работа
Вариант №1
Выполнила
Специальность
№
личного дела
Группа
Дисциплина ЭММ ПМ
Преподаватель
Вариант №1
Задача 1.1.
Условия задачи:
Инвестор, располагающий суммой в 300
тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акции А должно быть приобретено на сумму по
крайней мере в два раза большую, чем акции В,
причем последних можно купить не более чем на 100 тыс. ден. ед.
Дивиденды по акциям А составляют 8% в год, по акциям В -10%. Какую максимальную прибыль можно
получить в первый год?
Решение:
Математическая модель имеет вид.
F = 0,08x1 + 0,1x2 Þ max
- целевая функция (прибыль)
x1 + x2
£
300
x1
³
2x2 = x1 -2x2
³0
- ограничения по сумме вложений
x2 £ 100
x1 ³ 0; x2 ³ 0;
Управляющие переменные:
x1-
сумма капитала
вложенная в акции автомобильного концерна А
,
x2 – сумма капитала вложенная в акции
строительного предприятия В,
соответственно;
F – прибыль.
Система неравенств включает
ограничения по суммам вложений. Акции А
должно быть приобретено на сумму по крайней мере в два раза большую, чем акции В, причем последних можно купить не более
чем на 100 тыс. ден. ед.
Необходимые для работы
программы «Поиск решения» данные:
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
3
|
переменные
|
х1
|
х2
|
|
|
|
|
|
|
4
|
значения
|
|
|
|
|
<--свободные ячейки
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
6
|
цел-я функция
|
коэф-ты Cj
|
значение F
|
|
|
|
7
|
|
0,08
|
0,1
|
|
|
=СУММПРОИЗВ(В7:С7;В4:С4)
|
|
|
|
8
|
|
|
|
|
|
|
|
|
|
9
|
ограничения
|
коэф-ты аij
|
формула
|
знак
|
bi
|
|
10
|
1-ое
|
1
|
1
|
|
|
=СУММПРОИЗВ(В10:С10;В4:С4)
|
<=
|
300
|
|
11
|
2-ое
|
1
|
-2
|
|
|
=СУММПРОИЗВ(В11:С11;В4:С4)
|
>=
|
0
|
|
12
|
3-ие
|
0
|
1
|
|
|
=СУММПРОИЗВ(В12:С12;В4:С4)
|
<=
|
100
|
Диалоговое окно программы «Поиск
решения»
Установить целевую ячейку $F$7
Равной О max значению
Изменяя ячейки :$B$4:$C$4
Ограничения:
$F$10<=$H$10 v Линейная модель
$F$11>=$H$11 v
Неотрицательные значения
$F$12<=$H$12
Результат работы программы «Поиск
решения»
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
3
|
переменные
|
х1
|
х2
|
|
|
|
|
|
|
4
|
значения
|
200
|
100
|
|
|
<--свободные ячейки
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
6
|
цел-я функция
|
коэф-ты Cj
|
значение F
|
|
|
|
7
|
|
0,08
|
0,1
|
|
|
26
|
|
|
|
8
|
|
|
|
|
|
|
|
|
|
9
|
ограничения
|
коэф-ты аij
|
формула
|
знак
|
bi
|
|
10
|
1-ое
|
1
|
1
|
|
|
300
|
<=
|
300
|
|
11
|
2-ое
|
1
|
-2
|
|
|
0
|
>=
|
0
|
|
12
|
3-ие
|
0
|
1
|
|
|
100
|
<=
|
100
|
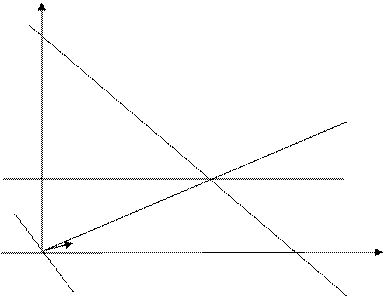
Графическое решение.
F = 0,08x1
+ 0,1x2 Þ max
x1 + x2 £ 300
x1 -2x2 ³0
x2
£ 100
x1 ³ 0; x2 ³ 0;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
200
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150
|
|
|
|
|
|
|
|
X1-2X2=0
|
|
|
A
|
|
|
B
|
|
|
|
|
|
|
100
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2=100
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|
100
|
|
200
|
|
300
|
|
х1
|
|
|
|
L
|
|
|
|
|
|
|
X1+X2=300
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Определим множество
решений неравенств:
1-ое
ограничение
x1 + x2 = 300
x1 0 300
x2 300
0
2-ое
ограничение
x1 -2x2 =0
x1 0 300
x2 0 150
3-ие
ограничение
x2 =100 – горизонтальная
прямая
2. Приравняем целевую функцию к нулю F = 0,08x1 + 0,1x2 =0
x1 0
1
x2 0
-0,8
через эти две точки проведем линию (L).
3. Построим
вектор-градиент и соединим его с началом координат
∆ (с1 ; с2 );
∆ (0,08
; 0,1 ).
4. При минимизации
целевой функции необходимо в направлении вектора-градиента. В нашем случае
движение линии уровня будет осуществляться до ее пересечения с точкой В, далее она выходит из области
допустимых решений. Именно в этой точке достигается максимум целевой функции.
x1 + x2 = 300
x2 =100
x1 = 300 -x2
x1 = 300 – 100 = 200; F = 0,08*200 + 0,1*100 = 16 + 10 = 26.
5. Ответ: max (F) =26 и достигается при x1 =200; x2 =100;
Рекомендуется вложить в
акции автомобильного концерна А, 200
тыс. ден. ед., в акции строительного предприятия В, 100 тыс. ден. ед., в первый год получим максимум прибыли 26 тыс.
ден. ед.
6. Если поставить задачу
минимизации, функциональную линию уровня необходимо смещать в направлении
противоположном вектору-градиенту ∆. Минимум целевой функции достигается
в точке 0 (0;0) следовательно можно записать min (F) = 0 и достигается при x1 = 0; x2 = 0.
Задача 2.1.
Для изготовления четырех видов
продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены
реализации каждого вида продукции приведены в таблице.
|
Тип сырья
|
Нормы расхода
сырья на одно изделие
|
Запасы сырья
|
|
А
|
Б
|
В
|
Г
|
|
I
|
1
|
2
|
1
|
0
|
18
|
|
II
|
1
|
1
|
2
|
1
|
30
|
|
III
|
1
|
3
|
3
|
2
|
40
|
|
Цена изделия
|
12
|
7
|
18
|
10
|
|
Требуется:
1. Сформулировать прямую
оптимизационную задачу на максимум выручки от реализации готовой продукции,
получить оптимальный план с помощью теорем двойственности.
2. Сформулировать
двойственную задачу и найти ее оптимальный план с помощью теорем
двойственности.
3. Пояснить нулевые
значения переменных в оптимальном плане.
4. На основе свойств
двойственных оценок и теорем двойственности:
·
проанализировать
использование ресурсов в оптимальном плане исходной задачи;
·
определить,
как изменятся выручка и план выпуска продукции при увеличении запасов сырья I и II видов на 4 и 3 единицы
соответственно и уменьшении на 3 единицы сырья III вида;
·
оценить
целесообразность включения в план изделия Д
ценой 10 ед., на изготовление которого расходуется по две единицы каждого
вида сырья.
Решение:
1. Математическая модель
имеет вид.
F = 18x1 + 30x2 + 40x3 min (стоимость ресурсов)
x1 + x2
+ x3 ³12
2x1 +x2 + 3x3 ³7 - стоимость ресурсов, затраченных на
производство единицы
x1 + 2x2 +3x3 ³18 продукции, при нормах расходах сырья
соответственно
0x1 + x2 +2x3 ³10 (А,
Б, В, Г).
Управляющие переменные:
x1 – двойственная оценка или теневая цена 1–ого ресурса
x2 – двойственная оценка или теневая цена 2–ого ресурса
x3 – двойственная оценка или теневая
цена 3–го ресурса
Необходимые для работы программы
«Поиск решения» данные:
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
3
|
переменные
|
х1
|
х2
|
х3
|
|
|
|
|
4
|
значения
|
|
|
|
<--свободные ячейки
|
|
|
|
5
|
|
|
|
|
|
|
|
|
6
|
цел-я функция
|
коэф-ты Cj
|
значение F
|
|
|
|
7
|
F
|
18
|
30
|
40
|
=СУММПРОИЗВ(В7:D7;В4:D4)
|
|
|
|
8
|
|
|
|
|
|
|
|
|
9
|
ограничения
|
коэф-ты аij
|
формула
|
знак
|
bi
|
|
10
|
1-ое
|
1
|
1
|
1
|
=СУММПРОИЗВ(В10:D10;В4:D4)
|
>=
|
12
|
|
11
|
2-ое
|
2
|
1
|
3
|
=СУММПРОИЗВ(В11:D11;В4:D4)
|
>=
|
7
|
|
12
|
3-ие
|
1
|
2
|
3
|
=СУММПРОИЗВ(В12:D12;В4:D4)
|
>=
|
18
|
|
13
|
4-ое
|
0
|
1
|
2
|
=СУММПРОИЗВ(В13:D13;В4:D4)
|
>=
|
10
|
Диалоговое окно программы «Поиск
решения»
Установить целевую ячейку $E$7
Равной О min значению
Изменяя ячейки :$B$4:$D$4
Ограничения:
$E$10: $E$13>=$G$10: $G$13
v Линейная модель
v
Неотрицательные значения
Результат работы программы «Поиск
решения»
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
3
|
переменные
|
х1
|
х2
|
х3
|
|
|
|
|
4
|
значения
|
7
|
0
|
5
|
<--свободные ячейки
|
|
|
|
5
|
|
|
|
|
|
|
|
|
6
|
цел-я функция
|
коэф-ты Cj
|
значение F
|
|
|
|
7
|
F
|
18
|
30
|
40
|
326
|
|
|
|
8
|
|
|
|
|
|
|
|
|
9
|
ограничения
|
коэф-ты аij
|
формула
|
знак
|
bi
|
|
10
|
1-ое
|
1
|
1
|
1
|
12
|
>=
|
12
|
|
11
|
2-ое
|
2
|
1
|
3
|
29
|
>=
|
7
|
|
12
|
3-ие
|
1
|
2
|
3
|
22
|
>=
|
18
|
|
13
|
4-ое
|
0
|
1
|
2
|
10
|
>=
|
10
|
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результ.
|
Нормир.
|
Целевой
|
Допустимое
|
Допустимое
|
|
Ячейка
|
Имя
|
значение
|
стоимость
|
Коэффициент
|
Увеличение
|
Уменьшение
|
|
$B$4
|
значения х1
|
7
|
0
|
18
|
2
|
18
|
|
$C$4
|
значения х2
|
0
|
1
|
30
|
1E+30
|
1
|
|
$D$4
|
значения х3
|
5
|
0
|
40
|
2
|
22
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результ.
|
Теневая
|
Ограничение
|
Допустимое
|
Допустимое
|
|
Ячейка
|
Имя
|
значение
|
Цена
|
Правая часть
|
Увеличение
|
Уменьшение
|
|
$E$10
|
1-ое формула
|
12
|
18
|
12
|
1E+30
|
4
|
|
$E$11
|
2-ое формула
|
29
|
0
|
7
|
22
|
1E+30
|
|
$E$12
|
3-ие формула
|
22
|
0
|
18
|
4
|
1E+30
|
|
$E$13
|
4-ое формула
|
10
|
11
|
10
|
14
|
4
|
3. Если продукция вошла в
оптимальный план хj >0, то в двойственных оценках она не убыточна, т.е.
стоимость ресурсов, затраченных на производство единицы продукции, равна ее
цене. Такие изделия эффективны, выгодны с точки зрения принятого критерия
оптимально. В нашей задаче – это предприятия вида А и Г. Если стоимость
ресурсов, затраченных на производство одной единицы продукции больше его цены,
то это изделие не войдет в оптимальный план из-за убыточности. В нашей задаче в
план выпуска не вошла продукция вида Б и В, потому что затраты по ним превышают
цену.
Этот факт можно
подтвердить, подставив в ограничения двойственной задачи оптимальные значения
вектора у:
у1 + у2 + у3
³12 Þ 1*7+1*0+1*5 =
12 = 12 Þ выгодно
2у1
+у2 + 3у3 ³7 Þ 2*7+1*0+3*5
= 29 > 7 Þ невыгодно
у1 + 2у2 +3у3
³18 Þ 1*7+2*0+3*5 =
22 > 18 Þ
невыгодно
0у1 + у2 +2у3
³10
Þ 0+1*0+2*5 = 10 = 10 Þ выгодно
4. На основе свойств
двойственных оценок и теорем двойственности:
·
проанализировать
использование ресурсов в оптимальном плане исходной задачи:
1-ый и 3-ий ресурсы имеют отличные от
нуля оценки: 7 и 5 - эти ресурсы
полностью используются в оптимальном плане и являются дефицитными, т.е
сдерживают рост целевой функции.
x1 + 2x2 + x3+
0 £18
правые части этих
ограничений равны левым частям
x1 +3x2 + 3x3+ 2x4 £40
1*18+2*0+1*0+0 = 18
1*18+3*0+3*0+2*11 = 40
2-ой ресурс используется не полностью
(29<30), поэтому имеет нулевую двойственную оценку (у2 = 0).
x1 +x2 + 2x3+ x4 £30
1*18+1*0+2*0+1*11 = 29<30.
Этот ресурс в меньшей
степени влияет на план выпуска продукции.
·
определить,
как изменятся выручка и план выпуска продукции при увеличении запасов сырья I и II видов на 4 и 3 единицы
соответственно и уменьшении на 3 единицы сырья III вида:
Ic =18+4=22
IIc =30+3=33
IIIc =40-3=37
∆Fmax =∆bi*yi
∆ Fmax =4*7+3*0-(3*5) = 28+0-15 = 13
В нашей задаче значение
целевой функции увеличивается на 13 ден.ед, план выпуска: x1 =
22; x2 =
0; x3 =
0; x4 =
7,5.
·
оценить
целесообразность включения в план изделия Д
ценой 10 ед., на изготовление которого расходуется по две единицы каждого
вида сырья.
αi - нормированные затраты ресурсов на производство
единицы новой продукции Д.
с – ожидаемая
прибыль
с1 - 2; с2 - 2; с3 - 2; с
-10
чистый доход Þ σ = с - ∑ αi yi
σ = 10 – (2*7+2*0+2*5) = (14+0+10) = 10 – 24 = -14
-14 <0 Þ производство изделия Д нецелесообразно.
Ответ: Общая
стоимость используемых ресурсов при
выпуске 18 единиц продукции А и 11
единиц продукции Г составит 326
ден.ед.
Вывод:
Предприятию безразлично, производить ли продукцию по оптимальному плану и
получить max прибыль
либо продать ресурсы по оптимальным ценам и возместить от продажи равные ей min затраты на ресурсы.
Задача 3.1
Промышленная группа
предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех
предприятий группы специализируется на выпуске продукции одного вида: первое
предприятие специализируется на выпуске продукции первого вида, второе
предприятие – продукции второго вида; третье предприятие – продукции третьего
вида. Часть выпускаемой продукции потребляемая предприятиями холдинга (идет на
внутреннее потребление), остальная часть поставляется за его пределы (внешним
потребителям, является конечным продуктом). Специалистами управляющей компании
получены экономические оценки αij (i = 1, 2, 3; j = 1, 2, 3) элементов технологической
матрицы А (норм расхода,
коэффициентов прямых материальных затрат) и элементов уi ветора конечной продукции Y.
Требуется:
1. Проверить
продуктивность технологической матрицы А = (αij) (матрицы коэффициентов прямых материальных затрат).
2. Построить баланс
(заполнить таблицу) производства и распределения продукции предприятий
холдинга.
0,1 0,2
0,1
А = 0,2 0,1
0
200
Y = 150
0 0,2
0,1 250
Решение
1. Проверка достаточного
условия продуктивности матрицы А.
Суммы
элементов столбцов матриц А 0,3 0,5 0,2 норма матрицы А
0,5
А = max (0,3; 0,5; 0,2) = 0,5 < 1 значит
матрица А продуктивная.
2.
Определим вектор валовой продукции.
1
0 0
Е =
0 1 0
0,9 -0,2
-0,1
Е-А = -0,2
0,9 0
0
0 1 0
-0,2 0,9
Е – единичная
матрица
|
1,175617
|
0,290276
|
0,130624
|
|
0,261248
|
1,175617
|
0,029028
|
|
0,058055
|
0,261248
|
1,117562
|
обр(Е-А) =
|
311,3208
|
|
235,8491
|
|
330,1887
|
х=
Расчет прямых
материальных затрат Хij, величин условно чистой продукции Zj. Заполнение таблицы производства и
распределения продукции.
|
Схема баланса производства и
распределения продукции
|
|
производящие структуры
|
потребляющие структуры
|
конечный продукт
|
валовой продукт
|
|
1-ая
|
2-ая
|
3-я
|
|
1-ая
|
31
|
47
|
33
|
200
|
311
|
|
2-ая
|
62
|
24
|
0
|
150
|
236
|
|
3-я
|
0
|
47
|
33
|
250
|
330
|
|
∑
|
93
|
118
|
66
|
|
|
|
усл.чист.прод.
|
218
|
118
|
264
|
600=600
|
|
|
вал.продукт
|
311
|
236
|
330
|
|
877=877
|
Расчет производственных затрат
Xij
= αij*Xj
x11
= 0,1*311=31,1 x12 = 0,2*236=47,2 x13 = 0,1*330=33
x21 = 0,2*311=62,2 x22 = 0,1*236=23,6 x23 = 0 *330=0
x31 = 0*311=0 x32 = 0,2*236=47,2 x33 = 0,1*330=33
Расчет условно-чистой продукции
Zj= Xj- Xij (по столбцам)
z1
= 311-(31+62+0)=311-93=218
z2 = 236- (47+24+47)=236-118=118
z3 = 330-(33+0+33)=330-66=264
Задача 4.1
В течении девяти
последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании
|
Неделя
|
Спрос
|
|
t
|
Y
|
|
1
|
10
|
|
2
|
14
|
|
3
|
21
|
|
4
|
24
|
|
5
|
33
|
|
6
|
41
|
|
7
|
44
|
|
8
|
47
|
|
9
|
49
|
Требуется:
1. Проверить наличие
аномальных наблюдений.
2. Построить линейную
модель Ỹ(t)= α0 +
α 1 t, параметры которой оценить МНК (Ỹ(t)) – расчетные, смоделированные
значения временного ряда.
3. Оценить адекватность
построенных моделей, используя свойства независимости остаточной компоненты,
случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7-3,7).
4. Оценить точность
моделей на основе использования средней относительной ошибки аппроксимации.
5. По одной построенной
модели осуществить прогноз спроса на следующие две недели (доверительный
интервал прогноза рассчитать при доверительной вероятности р =
70%).
6. Фактические значения
показателя, результаты моделирования и прогнозирования представить графически.
1.График временного ряда
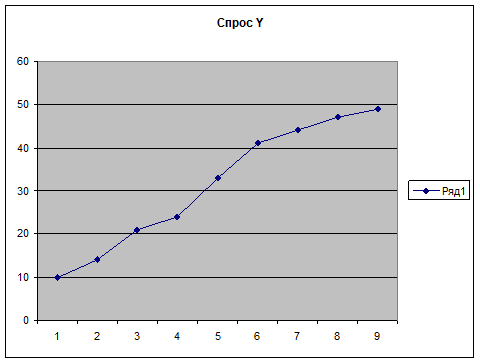
Требуется проверить
аномальный характер 5 наблюдения
Проверяемое
наблюдение
Оставшиеся
наблюдения
|
t
|
Y
|
|
1
|
10
|
|
2
|
14
|
|
3
|
21
|
|
4
|
24
|
|
6
|
41
|
|
7
|
44
|
|
8
|
47
|
|
9
|
49
|
Для оставшихся наблюдений вычислим:
|
Yср
=
|
31,44444
|
|
Sy
=
|
14,70639
|
|
t
=
|
0,105774
|
|
t
кр =
|
3,499483
|
Сравниваем t < t кр наблюдение 5 не является
аномальным, не требует замены.
2. Оценка параметров
модели.
Построим линейную
однопараметрическую модель регрессии Y от t.
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
|
Множественный R
|
0,986962273
|
|
|
|
|
|
R-квадрат
|
0,974094529
|
|
|
|
|
|
Нормированный R-квадрат
|
0,970393747
|
|
|
|
|
|
Стандартная ошибка
|
2,530449486
|
|
|
|
|
|
Наблюдения
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
1685,4
|
1685,4
|
263,21319
|
8,2267E-07
|
|
Остаток
|
7
|
44,82222222
|
6,403174603
|
|
|
|
Итого
|
8
|
1730,222222
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
|
Y-пересечение
|
4,944444444
|
1,838328932
|
2,68964077
|
0,0311019
|
0,59748727
|
|
t
|
5,3
|
0,326679624
|
16,22384627
|
8,227E-07
|
4,52752544
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
|
|
|
1
|
10,24444444
|
-0,244444444
|
|
|
|
|
2
|
15,54444444
|
-1,544444444
|
|
|
|
|
3
|
20,84444444
|
0,155555556
|
|
|
|
|
4
|
26,14444444
|
-2,144444444
|
|
|
|
|
5
|
31,44444444
|
1,555555556
|
|
|
|
|
6
|
36,74444444
|
4,255555556
|
|
|
|
|
7
|
42,04444444
|
1,955555556
|
|
|
|
|
8
|
47,34444444
|
-0,344444444
|
|
|
|
|
9
|
52,64444444
|
-3,644444444
|
|
|
|
|
|
|
|
|
|
|
Модель построена, ее
уравнение у t = 4,94+5,3 t
С каждой неделей спрос в
среднем возрастает на 5,3 млн.руб.
3. Оценка адекватности
построенной модели.
Для проверки свойства
случайности остаточной компоненты:
а) построить график
остатков;
б) сосчитать количество
поворотных точек р;
в) вычислить критическое
значение р кр.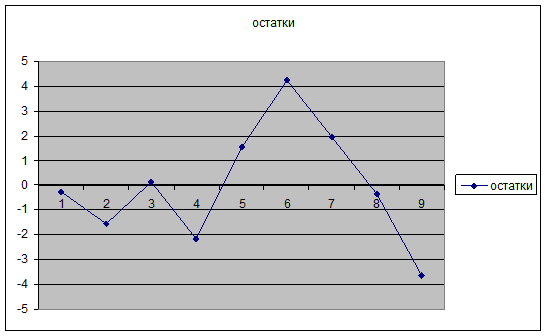
р = 5
р кр = 2,451105539
2*(9-2)/3-1,96*КОРЕНЬ((16*9-29)90)
Для проверки равенства
нулю математического ожидания остатков вычислить среднее значение Еср
Еср = 1,18424Е-15
Для проверки
независимости уровней ряда остатков:
а) вычислить d-статистику;
б) вычислить первый
коэффициент автокорреляции r(1).
суммкв(Е)= 44,82222 d=
1,167278
суммквразн(Е)= 52,32 r(1)=
0,267532
суммпроизв(Е)= 11,99136
Для проверки нормального
распределения остатков вычислить R/S-статистику
Е min= -3,644444444 R/S= 3,12253
E max= 4.255555556 S(E)= 2,53
Критический интервал (2,7
– 3,7)
R/S=3,12 принадлежит (2,7 – 3,7),
свойства нормального распределения остатков выполняются.
4. Для оценки точности
модели вычислить относительные погрешности для всех уровней исходного ряда,
определить среднюю относительную погрешность
0,024444
0,110317
0,007407
0,089352
0,047138
0,103794
0,044444
0,007329
0,074376
Еср.отн= 5,651141
5. Рассчитать точечную и
интервальную прогнозные оценки спроса на следующие две недели.
Воспользуемся построенной
моделью у t = 4,94+5,3 t
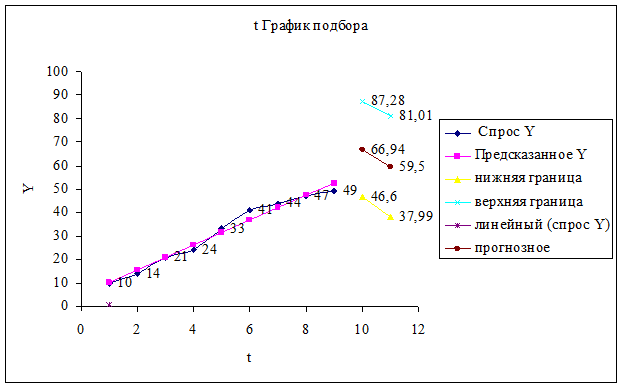
Следующие две недели t=11, точечный прогноз y = 4,94+5,3*11=63,24
у*= 63,24 t кр=
1,119159
u= 3,703834
t ср= 5 нижн.гр.= 59,53617
квадроткл(t)= 60 верх.гр.= 66,94383
С доверительной
вероятностью 70% можно утверждать, что спрос на следующие две недели будет от
59,54 до 66,94 млн.руб.
6. Результаты
прогнозирования показать на графике.