Задача 1
Определить величину и
направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня
находится воздух, слева от поршня и в резервуаре, куда опущен открытый конец
трубы – глицерин. Показание пружинного манометра – 20000 Па (вак). Дано: Н=5м, D= 180, d=90 мм.
Решение:
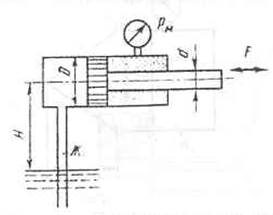
Для удержания поршня на
месте необходимо прижить силу, направленную от поршня, как показано на рисунке
жирной стрелкой. По величине эта сила должна уравновесить силу давления в 0,2
атм. со стороны жидкости. Сила давления жидкости
Н.
Ответ: 679,5 Н;
направлена вправо от поршня.
Задача 8
Жидкость (трансформаторное
масло) попадает в открытый верхний бак по вертикальной трубе длиной 
= 12 м, и диаметром d = 60 мм за счет давления воздуха в
нижнем замкнутом резервуаре. Определить давление р воздуха, при котором расход
будет равен Q = 6 л/с. Принять при этом 
= 8, Sкл = 0,5, 
= 1, Rе = 0,2 мм.
Решение:
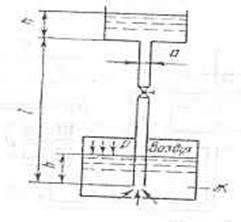
Для эквивалентной
шероховатости Rе = (
т / 0,11)4 d,
откуда т = 0,0254.
Перепад давлений
вычисляется по формуле
Р – Ратм = (+ 
) 
Суммарные потери напора
= (
т * 
) * 
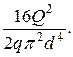
В результате получаем
+ т * 
= 12,4
= 2,7
Р – Ратм = 24
кПа.
Поскольку атмосферное
давление равно 100 кПа, то Р = 124 кПа.
Ответ: Р = 1,24 атм.
Задача 17
Из бака А, в котором
поддерживается постоянный уровень, вода протекает по цилиндрическому насадку
диаметром d=25 мм в бак В, из которого сливается
в атмосферу по короткой трубе диаметром D=31 мм, снабженной краном. Определить
наибольшее значение коэффициента сопротивления крана 
, при котором истечение из насадка будет осуществляться в
атмосферу. Потери на трение в трубе не учитывать. При этом 
см, Н = 128 см.
Решение:
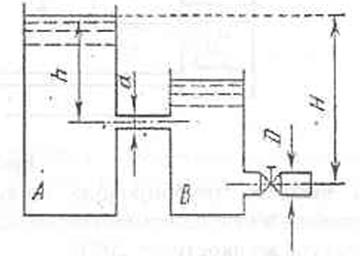
Максимальное
сопротивление крана будем находить из условия равенства расхода воды через
трубу диаметром d=30 мм и через трубу диаметром D=37 мм, причем сопротивление при
истечении воды через трубу d=30 мм не учитываем. Запишем это равенство расхода:
После элементарных
преобразований:
Откуда:
.
Ответ: 0,24.
Задача 22
Центробежный насос
производительностью Q=14 л/с работает при частоте вращения
п=1475 об/мин. Определить
допустимую высоту всасывания, если диаметр всасывающей трубы d=100 мм, а ее длина l=2,5 м. Коэффициент кавитации в формуле
Руднева принять равным С=1200.
Температура воды t=20°С. Коэффициент сопротивления колена =0,2. Коэффициент сопротивления входа в трубу 
=1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.
Решение:
Расход воды
рассчитывается по формуле:
.
Выразим из этой формулы
искомую величину (высоту) и подставим исходные данные задачи, учитывая, что 14
л/с равен 0,014 м3/с:
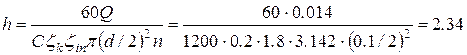м.
Ответ: 2,34 м.
Задача 30
Поршневой насос простого
действия с диаметром цилиндра D=90 мм, ходом поршня S=280 мм, числом двойных ходов в
минуту п=80 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
систему гидропровода. При какой частоте вращения должен работать включенный
параллельно шестеренный насос с начальным диаметром шестерен d=72 мм, шириной шестерен b=70 мм, числом зубьев z=30 и объемным КПД hоб=0,86, чтобы количество подаваемой
жидкости удвоилось?
Решение:
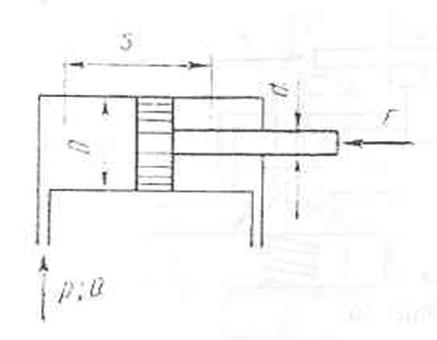
Поршневой насос простого
действия с диаметром цилиндра D=90 мм, ходом поршня S=280 мм, числом двойных ходов в минуту
п=80 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
количестве
м3/мин.
Для расчета минутной подачи насосов с
двумя одинаковыми шестернями можно пользоваться формулой
Q = η0A(Dг-
A)bN ,
где η0 - объемный КПД
насоса, зависящий от конструкции, технологии изготовления и давления насоса и
принимаемый равным 0,7-0,95; А - расстояние между центрами шестерен, равное
диаметру начальной окружности D; Dг - диаметр окружности головок
зубьев; b - ширина шестерен; N - частота вращения ротора, об/мин.
Согласно условию задачи,
количество подаваемой жидкости должно удвоиться, тогда искомая частота
вращения:
N = η0A(Dг-A)b / (2∙Q) = 0,9∙30∙(72-30)∙65 / (2∙0,002) =
302 об/мин.
Ответ: 302 об/мин.
Задача
40
Пользуясь характеристикой
гидромуфты, определить расчетный и максимальный моменты, передаваемые ею, а
также передаточное отношение, коэффициент полезного действия и скольжение при
этих режимах, если активный диаметр гидромуфты D=420 см, частота вращения ведущего
вала n=1400 об/мин, рабочая жидкость – трансформаторное масло. Как
изменяется передаваемые крутящий момент
и мощность, если частоту вращения ведущего вала увеличить в полтора раза?
Решение:
В гидромуфте
(гидропередача без внешней опоры) момент на турбине всегда равен моменту на
насосе, но передача энергии в ней происходит с определенными потерями,
характеризуемыми в рабочем режиме значением К.П.Д. Поскольку
моменты колес раны, то К.П.Д. численно равен отношению частоты вращения
турбины n2 к частоте вращения насоса n1, т.е. передаточному
отношению i ( i= n2/n1).
Момент гидромуфты Мг подчиняется зависимости
М = λi·ρ·(n
/ 60)2·Da,
где:
λi -
коэффициент момента, являющийся параметром гидромуфты данного типа при заданном
значении i, ρ-плотность РЖ, Da- активный диаметр, равный
наибольшему диаметру рабочей полости гидромуфты.
Отсюда искомый активный диаметр:
Da = М / (λi·ρ·(n
/ 60)2) = 350 / (60∙10-7 ∙ 8600 ∙ (1100
/ 60)2) = 0,202 м.
Построим внешнюю
(моментальную) характеристику гидравлической муфты. В эту характеристику входят:
1) момент муфты: М = 350 Н∙м;
2) коэффициент момента λi =
60∙10-7 мин2/м;
3) активный диаметр: Da
= 0,202 м;
4) частота вращения п =
1400 об/мин.
Ответ: 350 Н∙м.
Список
литературы
1.
Башта
Т.М., Руднев С.С. Гидравлика, гидромашины и гидропривод. – М.: Машиностроение,
1982.
2.
Дергачев
Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
3.
Задачник
по гидравлике, гидромашинам и гидроприводу / под ред. Б.Б. Некрасова. – М.:
Высшая школа, 1989.
4.
Осипов
П.Е. Гидравлика, гидромашины и гидропривод. – М.: Лесная промышленность, 1981.
5.
Юфин
А.П. Гидравлика, гидромашины и гидропривод. – М.: