Содержание
Содержание. 2
Условие. 3
Решение. 3
Задание №1. 3
Начальные
данные. 3
График
временного ряда. 5
Первичный
статистический ананлиз. 5
Вычисление
среднего значения. 5
Вычисление
дисперсии. 5
Вычисление
актокорреляции. 6
Вычисление
автоковариации. 7
Построение
графика автокорреляционной функции. 8
Выводы.. 8
Проверка
гипотезы наличия тренда. 8
Запись функции
разложения ряда. 8
Поверка
гипотезы наличия тренда. 8
Выбор модели
неслучайных компонент. 10
Визуальная
оценка графика временного ряда. 10
Оценка по R2 10
Отбор функции. 10
Вычисление
прогноза. 11
Приложение
«результат прогнозирования полиномом 4-ой степени» 12
Условие
Построить график
временного ряда (курс евро за месяц)
Провести
первичный статистический анализ временного ряда, включая вычисление среднего
значения, меря разброса, автокорреляционной и автоковариационной функции,
построить коррелограмму. Сделать соответствующие
выводы
Записать
основное разложение временного ряда и проверить гипотезу о наличии неслучайных
компонент в этом разложении
Построить
уравнения для неслучайных компонент, присутствие которых в модели было
доказано. Обосновать выбор формы модели. Привести несколько вариантов
построенных моделей и обоснованно (по результатам эконометрического анализа)
выбрать наилучший
Сделать выводы
по всем полученным результатам и вычислить прогнозные значения по наиболее
оптимальной модели. Результаты прогнозирования показать на графике
Все вычисления
производить с помощью Microsoft Excel
Решение
Задание №1
Начальные
данные
|
Номер
|
Дата
|
Курс Euro
|
|
1
|
01.10.2005
|
34,3074
|
|
2
|
04.10.2005
|
34,2185
|
|
3
|
05.10.2005
|
34,1339
|
|
4
|
06.10.2005
|
34,1843
|
|
5
|
07.10.2005
|
34,3960
|
|
6
|
08.10.2005
|
34,6245
|
|
7
|
11.10.2005
|
34,5379
|
|
8
|
12.10.2005
|
34,3331
|
|
9
|
13.10.2005
|
34,2412
|
|
10
|
14.10.2005
|
34,2959
|
|
11
|
15.10.2005
|
34,3576
|
|
12
|
18.10.2005
|
34,4746
|
|
13
|
19.10.2005
|
34,3082
|
|
14
|
20.10.2005
|
34,1248
|
|
15
|
21.10.2005
|
34,2948
|
|
16
|
22.10.2005
|
34,4085
|
|
17
|
25.10.2005
|
34,2009
|
|
18
|
26.10.2005
|
34,1874
|
|
19
|
27.10.2005
|
34,4634
|
|
20
|
28.10.2005
|
34,4685
|
|
21
|
29.10.2005
|
34,5300
|
|
22
|
01.11.2005
|
34,3946
|
|
23
|
02.11.2005
|
34,2743
|
|
24
|
03.11.2005
|
34,3795
|
|
25
|
04.11.2005
|
34,4338
|
|
26
|
08.11.2005
|
33,9417
|
|
27
|
09.11.2005
|
33,8194
|
|
28
|
10.11.2005
|
33,9306
|
|
29
|
11.11.2005
|
33,9077
|
|
30
|
12.11.2005
|
33,8000
|
|
31
|
15.11.2005
|
33,8636
|
|
32
|
16.11.2005
|
33,7577
|
|
33
|
17.11.2005
|
33,7895
|
|
34
|
18.11.2005
|
33,6810
|
|
35
|
19.11.2005
|
33,7730
|
|
36
|
22.11.2005
|
33,8992
|
|
37
|
23.11.2005
|
33,8037
|
|
38
|
24.11.2005
|
33,9952
|
|
39
|
25.11.2005
|
33,9431
|
|
40
|
26.11.2005
|
33,8479
|
График
временного ряда
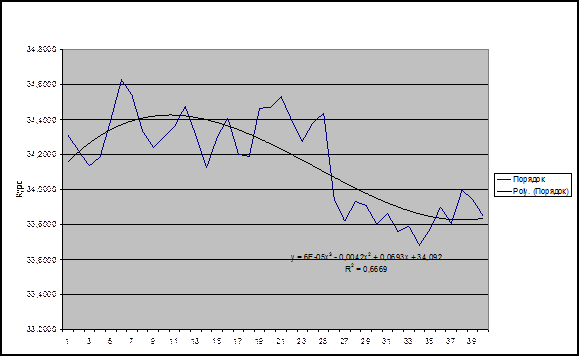
Первичный статистический анализ
Вычисление
среднего значения
Среднее значение
находится по формуле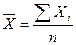 
Среднее значение
равно 34,1582
Вычисление
дисперсии
Среднее отклон6ение
находится по формуле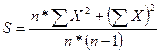 
Среднее значение
равно 0,0717
Вычисление
автокорреляции
Для вычисления
автокорреляции сдвинем ряд на определенное количество периодов (для 40
значения) последовательно найдем корреляцию «сдвинутых» рядов для 10 периодов =
l = 1..10
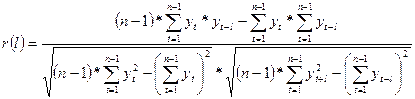
Таблица расчетов
приведена ниже:
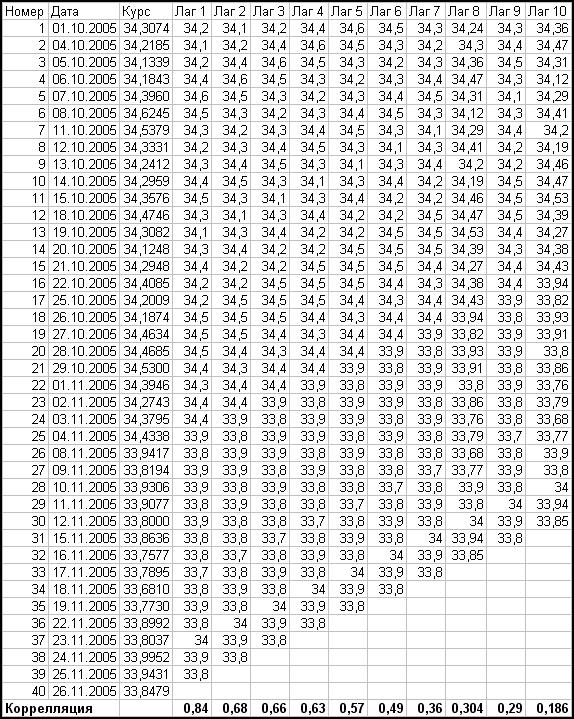
Вычисление
автоковариации
Аналогичным
образом рассчитаем ковариацию
Построение графика автокорреляционной функции
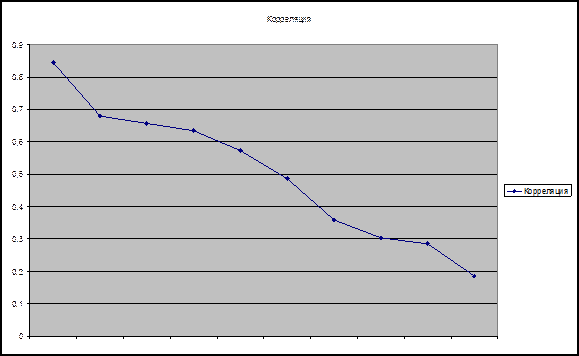
Выводы
Так как
максимальное значение автокорреляционной функции наблюдается для l = 1, то
исследуемый ряд не содержит циклических и сезонных компонент
Проверка гипотезы наличия тренда
Запись
функции разложения ряда
Так как мы
проверили гипотезу отсутствия сезонной и циклической составляющей, ряд можно
разложить следующим образом:
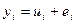(тренд и случайная
компонента)
Поверка
гипотезы наличия тренда
1.
Проранжируем ряд в порядке
возрастания
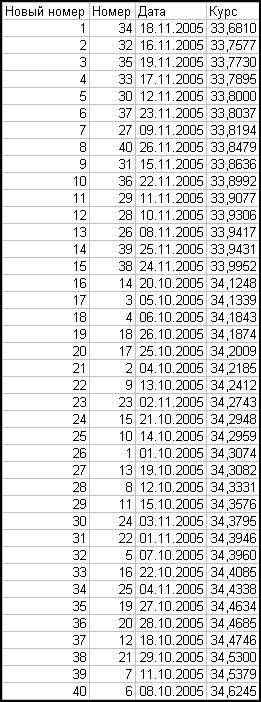
2.
Медианное значение равно (Y20+Y21)/2 = 34,2097
3.
Длинна самой длинной серии (подряд идущие значения больше
или меньше медианного значения) равна 15
4.
Число серий составляет 8 серии (подряд идущие значения
больше или меньше медианного значения)
5.
Проверяем выполнение следующих неравенств
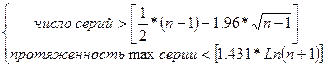
Таким образом:
8>7,7598
(выполняется)
8<5,314122
(не выполняется)
Значит гипотеза
об отсутствии тренда временного ряда отвергается с надежностью, лежащей между
0,9025 и 0,95
Выбор модели неслучайных компонент
Визуальная
оценка графика временного ряда
Так как ряд не
является ограниченным снизу или сверху и исходя из его внешнего вида можно
предположить наличие кубического полиномиального тренда
График данного
тренда приведен на исходном графике временного ряда
Оценка
по R2
Для оценки по
критерию R2 рассчитаем его
для нескольких возможных линий трендов
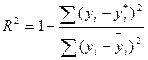, то есть какая часть вариации зависимой переменной
объясняется уравнением регрессии
1.
Линейный (R2 = 0.5108)
2.
Квадратичный (R2 = 0.5981)
3.
Кубический полном (R2 = 0,6669)
4.
Показательная функция (R2 = 0.5119)
5.
Полином четвертой степени (R2 = 0.7192)
Для расчета
функции R2 = воспользуемся
средствами excel
Отбор
функции
По критерию R2 наиболее
подходящей функцией является полином четвертой степени.
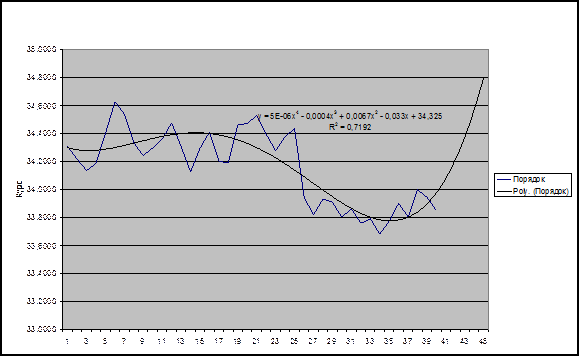
Так как нам в
дальнейшем придется рассчитывать прогноз, то примем в качестве наиболее
подходящей полином третьей степени, так как прогнозирование полиномом четвертой
степени может сильно «качнуть хвост», результат прогнозирования в приложении
Функция полинома
3 степени
y = 6E-05x3 - 0,0042x2 + 0,0693x + 34,09
Вычисление прогноза
По функции
полнома 3 степени вычислим прогноз на 5 дней
|
33,83359852
|
|
33,84807218
|
|
33,86821356
|
|
33,89434908
|
|
33,92680512
|
Построим график
функции
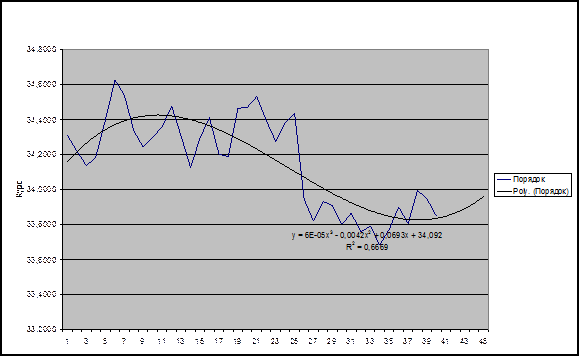
Приложение «результат прогнозирования полиномом 4-ой
степени»
