Задача 1
Для
изготовления продукции двух видов А и Б
предприятие расходует ресурсы, а от реализации этой продукции получает
доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции,
запасах расходуемых ресурсов, имеющихся в распоряжении предприятия, и выручки
от реализации готовой продукции приведены в таблице.
|
Наименование ресурсов
|
Норма затрат
на
|
Объем
ресурса
|
|
Продукт А
|
Продукт В
|
|
Сырье (кг)
|
1
|
2
|
111
|
|
Оборудование (ст.час.)
|
4
|
4
|
268
|
|
Трудоресурсы(чел.час.)
|
3
|
7
|
414
|
|
Цена реализации (руб.)
|
375
|
406
|
|
Задача предприятия
заключается в том, чтобы разработать программу выпуска, обеспечивающую
получение максимальной выручки от реализации готовой продукции.
Требуется :
1. Построить математическую модель оптимизации
выпуска продукции и записать ее в форме задачи линейного программирования.
2. Используя графический метод решения задачи линейного
программирования, найти оптимальную программу выпуска продукции.
3. Записать задачу, двойственную к задаче оптимизации выпуска
продукции.
4. Используя условия «дополняющей нежесткости», найти оптимальное
решение двойственной задачи.
5. Привести экономическую интерпретацию переменных и оптимального
решения двойственной задачи.
6.
Провести графический анализ устойчивости изменения объемов используемых
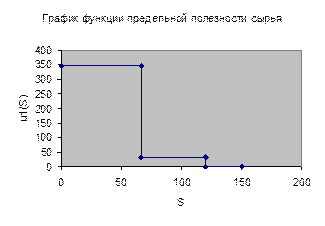
ресурсов. Найти функции предельной полезности ресурсов и построить их графики.
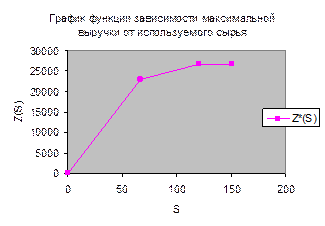
Определить функциональную зависимость максимальной выручки объемов используемых
ресурсов, построить графики этих функций.
Решение.
1.1. В нашей задаче необходимо определить месячные объемы выпуска
продукции вида А и Б. Обозначим эти объемы как переменные модели:
х1 – месячный объем выпуска продукции А,
х2 – месячный объем выпуска продукции Б.
Используя данные таблицы, получим:
расход сырья = х1 +2х2,
затраты времени работы оборудования =
4х1 + 4х2,
затраты рабочего времени = 3х1 + 7х2.
Так как ежемесячный расход ресурсов не может превышать их максимально
возможный месячный размер, то имеем ограничения
|
х1
+2х2£
111
|
|
4х1
+ 4х2£
268
|
|
3х1
+ 7х2£
414
|
Еще одно неявное ограничение состоит в том, что переменные х1
и х2 должны быть неотрицательны, т.е. х1 ³0,
х2³0.
Целевая функция модели должна выражать основную цель деятельности
предприятия. В нашем примере это получение максимальной выручки от реализации
произведенной в течении месяца продукции. Если обозначить функцию размера
выручки через Z, то Z = 375х1 + 406х2,
а основная
цель предприятия может быть выражена так:
Максимизировать целевую функцию Z=375х1 + 406х2,
Перепишем это условие в следующей форме: Z = 375х1 + 406х2® max.
Таким образом,
математическая модель оптимизации выпуска продукции может быть записана в следующем виде.
Найти неизвестные значения переменных х1 и х2,
удовлетворяющие ограничениям
|
х1
+2х2£
111
|
|
4х1
+ 4х2£
268
|
|
3х1
+ 7х2£
414
|
|
х1
³0,
х2³0
|
и
доставляющих максимальное значение целевой функции Z = 375х1 + 406х2® max.
Построенная модель
является задачей линейного программирования. Любое решение, удовлетворяющее
ограничениям модели, называется допустимым, а допустимое решение, доставляющее
максимальное значение целевой функции, называется оптимальным.
1.2. Нахождение
оптимальной производственной программы выпуска продукции.
Решение задачи линейного программирования с двумя переменными может
быть получено графическим способом.
Построим
множество допустимых решений или область допустимых решений. Проводим
перпендикулярные оси координат: горизонтальная – ось Ох1,
вертикальная - Ох2. Условия
неотрицательности переменных х1
³0,
х2³0
показывают, что область допустимых решений будет лежать в первом квадранте
системы координат. Для изображения на плоскости множества точек, координаты
которых удовлетворяют оставшимся ограничениям модели, рассмотрим уравнения,
получаемые из неравенств модели заменой знака «£» на знак «=». В
результате такой замены получим три линейных уравнения прямых:
|
х1
+2х2= 111
|
(1)
|
|
4х1
+ 4х2= 268
|
(2)
|
|
3х1
+ 7х2= 414
|
(3)
|
|
х1
³0,
х2³0
|
|
Для того, чтобы провести на плоскости прямую линию, достаточно знать
любые две различные точки, лежащие на этой прямой. Рассмотрим уравнение первой
прямой. Если положить х1 = 0, то х2 =55,5,
а при х2 = 0, х1 = 111. Обозначим эту прямую как
линия (1).
Прямая (2) проходит через точки с координатами (0;67) и (67;0).
Прямая (3) проходит через точки с координатами (0;59,1) и (138;0).
Каждая прямая делит плоскость на две полуплоскости. Точки
расположенные по одну сторону прямой, удовлетворяют соответствующему
неравенству, а точки, расположенные по другую сторону, не удовлетворяют. Для
того, чтобы определить искомую полуплоскость, выбирается некоторая «тестовая»
точка и ее координаты подставляются в левую часть неравенства. Если для этой
точки неравенство выполняется, то она лежит в искомой полуплоскости, т.е. все
точки этой полуплоскости удовлетворяют неравенству модели. Если же для «тестовой»
точки неравенство не выполняется, то искомой будет та полуплоскость, которая не
содержит эту точку. Взяв в качестве «тестовой» точку с координатами (0;0),
убеждаемся, что она удовлетворяет всем неравенствам модели.
Следовательно, все полуплоскости, соответствующие неравенствам модели,
содержат точку (0,0).
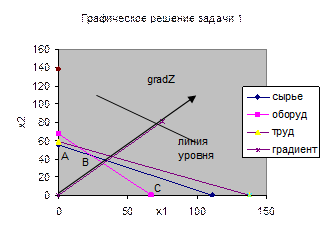
Точки множества допустимых решений должны удовлетворять всем
ограничениям. Следовательно, множество допустимых решений является пересечением
всех допустимых полуплоскостей и представляет собой многоугольник АВСО. Любая
точка, расположенная внутри этого многоугольника или на любом отрезке его
границы, является допустимым решением, т.е.
удовлетворяет всем ограничениям модели.
Для нахождения оптимального решения задачи необходимо определить
направление возрастания целевой функции.
Вектор, компоненты которого являются коэффициентами целевой функции
при переменных х1 и х2, называют вектором – градиентом
целевой функции и обозначают grad Z.
Целевая функция может возрастать до тех пор, пока линии уровня
соответствующие возрастающим значениям этой функции, пересекают область
допустимых решений. Точка пересечения области допустимых решений и линии
уровня, соответствующей максимально возможному значению целевой функции, и будет
точкой максимума.
На рисунке видно, что оптимальное решение соответствует точке В,
лежащей на пересечении прямых (1) и (2). Поэтому ее координаты находим как
решение системы линейных уравнений, задающих эти прямые:
|
х1
+2х2= 111
|
|
4х1
+ 4х2= 268
|
Решая эту систему находим х1* = 23, х2*= 44 .
При этом значение целевой функции Z = 375х1* + 406х2*= 26489.
Полученное решение означает, что предприятию необходимо ежемесячно
производить 23 единицы продукции А и 44
единицы продукции Б, что позволит ему получать максимальную месячную выручку в
размере 26489 рублей.
1.3. Построение
двойственной задачи.
Найти неизвестные значения переменных u1, u2, u3 , удовлетворяющих
ограничениям:
|
u1
+ 4u2 + 3u3 ³ 375
|
|
2u1 + 4u2 + 7u3 ³ 406
|
|
u1 ³0, u2 ³0,
u3 ³ 0
|
и доставляющих минимальное значение целевой функции
W
= 111u1 + 268u2 + 414u3 ® min.
1.4. Нахождение
оптимального решения двойственной задачи.
Для рассматриваемой нами задачи условия «дополнительной нежесткости»
имеют вид:
u1 (111 - x1-
2x2 )= 0 x1(u1
+ 4u2 + 3u3 - 375)= 0
u2(268 - 4x1
– 4x2)= 0 x2(2u1
+ 4u2 + 7u3 - 406) = 0
u3(414 - 3x1
– 7x2)= 0 u1 ³0, u2 ³0,
u3 ³ 0,
Подставляя в них найденные значения х1* = 23, х2*=
44, получим:
так как х1* = 23,
то u1 + 4u2 + 3u3 - 375= 0
так как х2* = 44,
то 2u1 + 4u2 + 7u3 - 406= 0
так как 414 - 3x1
– 7x2¹0,
то u3*
= 0.
Получаем систему уравнений: u1 + 4u2 + 3u3 - 375= 0
2u1
+ 4u2 + 7u3 - 406= 0
u3=0
Решая эту систему, находим оптимальные значения переменных двойственной
задачи:
u1* = 31, u2* = 86, u3* = 0
Вычислим оптимальное значение целевой функции двойственной задачи:
W = 111
× 31 + 268 × 86 + 414 × 0 = 26489, т.е. Z* = W*, что соответствует первой теореме двойственности.
1.5. Экономическая
интерпретация переменных и оптимального решения двойственной задачи.
Для
исследуемой задачи оптимизации производственной программы получим
u1
– стоимостная оценка сырья, ее размерность [руб./1 кг сырья];
u2
– стоимостная оценка времени работы оборудования, ее размерность [руб./1
ст.час];
u3
– стоимостная оценка трудовых ресурсов, [руб./1 чел.-час];
u1*
= 31 означает, что при изменении количества сырья с 31 кг до 31 + Δs, изменение максимальной
суммарной выручки составит u1*
Δs (руб.) = 31Δs (руб).
u2*
= 86 означает, при изменении месячного количества оборудования с 86 стан.-час
до 86 + Δm,
изменение максимальной суммарной выручки составит u2* Δm (руб.) = 86Δm (руб).
u3*
= 0 означает, что ни увеличение, ни
уменьшение месячного размера трудоресурсов не приведет к изменению оптимального
значения суммарной выручки .
1.6. Графический
анализ устойчивости сырья
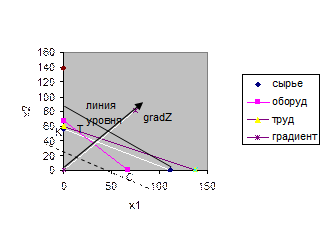
Количество используемого сырья S=х1 + 22 .
Если SÎ[0; S(С)], то точкой максимума является точка
E(0; x1) пересечения оси Ох1 и
прямой ограничения по сырью (1).
Если SÎ[S(С); S(Т)], то точкой максимума является
точка R(x1; x2) отрезка CТ пересечения прямой
ограничения по сырью и прямой (2)
Если SÎ[S(Т); ¥], то точкой максимума
является точка Р(0; x2) пересечения прямой (3) и оси Ох2.
Координаты точки Е находятся из системы уравнений
х1 + 2х2
= S
х2 = 0
Решаем ее:
х1 = S , х2 = 0.
Z*(S) = 375х1* + 406х2*
=345S; u1 = 345; u2= 0; u3
= 0
Координаты точки R
находим из системы уравнений
х1 + 2х2 = S
4х1 + 4х2 =268
Решаем ее:
х1 = (268 - 2S)/2, х2 = (4S-268)/4.
Z*(S) = 375х1* + 406х2* = 375 ´ (268 - 2S)/2 + 406´ (4S-268)/4 = 31S+ 23048;
u1 = 31; u2=
0; u3 = 0.
Координаты точки Т находим из системы
уравнений
|
4х1
+ 4х2= 268
|
|
3х1
+ 7х2= 414
|
Решаем ее:
х1 = 13,75, х2 = 53,25.
Z*(S) = 375х1*
+ 406х2* =
375 ´ 13,75+ 406´ 53,25=26775,75;
u1
= 0; u2= 0; u3 = 0.
S(C)= х1 + 2х2
=67+2´0=67
S(Т)= х1
+ 2х2 =13,75+2´53,25=120,25
|
S
|
0£S<67
|
67£S<120,25
|
S³120,25
|
|
u1*(S)
|
345
|
31
|
0
|
|
Z*(S)
|
345S
|
31S+ 23048
|
26775,75
|
Интервал устойчивости [67;120,25)
Задача 2.
Малое предприятие намерено организовать в следующем квартале выпуск продукции А и Б,
пользующейся высоким спросом на рынке. Предприятие располагает необходимым
сырьем и оборудованием и может привлечь квалифицированных рабочих на условиях почасовой оплаты, но не имеет
средств на оплату труда рабочих. Для этого оно может получить в банке кредит
сроком на три месяца под 40% годовых с погашением кредита и процентов по нему в
конце квартала.
Информация о нормах затрат сырья, оборудования и трудовых ресурсов,
объемах сырья и парка оборудования, имеющихся в распоряжении предприятия,
размер выручки от реализации продукции А и Б приведены в таблице:
|
Наименование ресурсов
|
Норма затрат на
|
Объем
ресурса
|
|
Продукт А
|
Продукт В
|
|
Сырье (кг)
|
12
|
3
|
6480
|
|
Оборудование (ст.час.)
|
6
|
3
|
4320
|
|
Трудоресурсы(чел.час.)
|
13
|
3
|
?
|
|
Цена реализации (руб.)
|
6295
|
1560
|
|
Целью организации выпуска новой продукции является получение
максимальной суммарной прибыли, которая определяется как разность между
суммарной выручкой, полученной от реализации произведенной за квартал продукции
А и Б, и затратами, связанными с обеспечением кредита (возврат суммы кредита
и начисленных процентов).
Требуется:
1. Построить математическую модель оптимизации выпуска продукции с
использованием кредита для выплаты зарплаты рабочими с произвольной почасовой
ставкой t (руб./чел.-час) оплаты труда.
2. Определить оптимальную программу выпуска продукции, максимальную
прибыль, необходимый размер кредита, сумму уплаченных процентов и потребность в
трудовых ресурсах, если почасовая ставка t оплаты труда равна 10 руб./чел.-час.
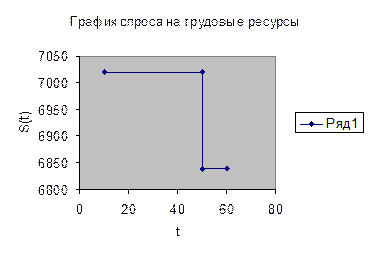
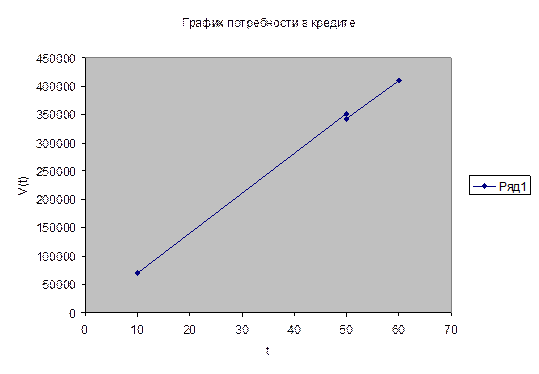
3. Найти функцию спроса на трудовые ресурсы, как функцию почасовой
ставки оплаты труда t, построить график этой функции.
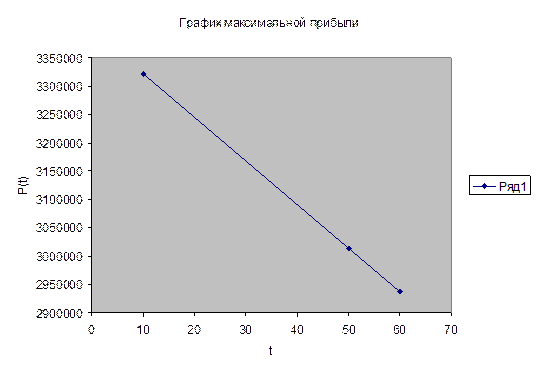
Исследовать зависимость размеров максимальной прибыли и кредита, обеспечивающего ее получение, от
почасовой ставки t
оплаты труда в диапазоне от 10 до 60 рублей за чел.-час. Найти функции, выражающие эти зависимости, и
построить их графики.
Решение.
2.1 Построение математической
модели оптимизации выпуска продукции.
Для построения модели введем следующие обозначения:
х1 – объем выпуска продукции А,
х2 – объем выпуска продукции Б,
S –
потребность в трудовых ресурсах,
t – почасовая
ставка оплаты труда,
V – размер
кредита,
Z – выручка от
реализации произведенной продукции,
P – прибыль
предприятия.
Выразим в математической форме основные условия и ограничения
рассматриваемой задачи.
Ограничения по использованию сырья: 12x1 + 3x2 £6480;
Ограничения по использованию оборудования: 6x1 + 3x2 £ 4320;
Потребность в трудовых ресурсах S определяется необходимыми затратами труда для выпуска продукции
в объемах х1 и х2:
S = 13x1 + 3x2 .
Размер необходимого кредита определяется, исходя из потребности в
трудовых ресурсах S и
почасовой ставки оплаты труда t,
т.е.
V=tS = t(13x1 + 3x2).
Выручка от реализации произведенной продукции:
Z = 6295x1 + 1560x2
Сумма расходов по обслуживанию кредита определяется размером
возвращаемого кредита и процентов по нему, т.е. равна
40%
3
V + (¾¾ ´ ¾¾¾)V = V + 0.1V = 1.1V.
12
100%
Прибыль предприятия определяется как разность
между выручкой и расходами по обслуживанию кредита, т.е.
Р = Z – 1.1V.
Подставляя в эту формулу выражения для Z и V, получим
Р = (6295x1 + 1560x2)– 1,1 t(13x1 + 3x2)
= (6295 – 14,3t)х1 + (1560 – 3,3 t)х2
Следовательно, математическая
модель оптимизации выпуска продукции с привлечением кредитных ресурсов для
оплаты труда рабочих принимает следующий
вид:
Найти неизвестные значения объемов выпуска х1, х2,
удовлетворяющих ограничениям
12x1
+ 3x2 £6480
6x1
+ 3x2 £ 4320 (1)
х1³0, х2³0,
и доставляющих максимальное значение целевой функции:
Р = (6295
– 14,3t)х1 +
(1560 – 3,3 t)х2 → max.
При этом необходимый размер кредита V определяется по формуле:
V = tS = 13tx1* + 3tx2*,
где х1*, х2* - оптимальное решение задачи (1).
Модель (1) представляет собой задачу
параметрического линейного программирования, так как в ее условиях содержится
параметр t, от значения
которого зависит оптимальное решение.
2.2 Определение
оптимальной программы выпуска продукции.
При фиксированной ставке оплаты труда t = 10 руб./чел.-час. математическая
модель (1) примет вид:
12x1
+ 3x2 £6480
6x1 + 3x2 £ 4320
х1³0,
х2³0, Р = 6152 х1 + 1527х2
→ max.
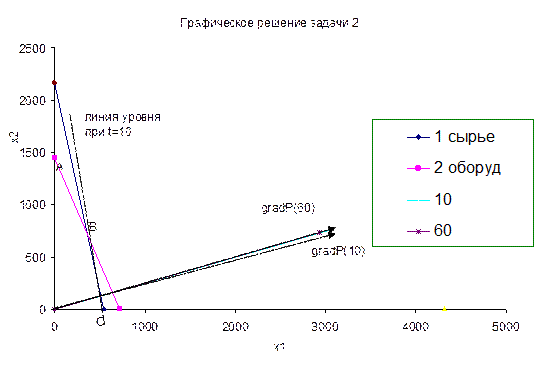
Графическое решение задачи изображено на рис. Точкой максимума
является точка В с координатами х1*
= 360, х2*= 720.
Максимальный размер прибыли:
Р* = 6152´360
+ 1527 ´720= 3314160 (руб.),
Размер необходимого кредита:
V* = 13tx1* +
3tx2* = 13´10´360 + 3´10´720 =68400 руб.,
Сумма уплаченных процентов: 0,1V* = 0,1´ 68400= 6840руб.
Потребность в
трудовых ресурсах: S* =
13x1* +3
x2*
= 6840(чел.-час.).
2.3 Нахождение
функции спроса на трудовые ресурсы
Потребность в трудовых ресурсах
S для обеспечения оптимального выпуска в объемах х1*,
х2* определяются соотношением:
S* = 13x1* + 3x2*,
Но оптимальный план выпуска Х* = (x1* , x2*), зависит от почасовой ставки t оплаты труда.
Следовательно, величина S также зависит от t, т.е. потребность в трудовых ресурсов S есть некоторая функция от параметра t.
Найдем эту функцию. Для этого рассмотрим модель (1) и определим оптимальные
планы выпуска Х* = (x1*
, x2*)
при различных значениях t,
используя графический метод решения задачи линейного программирования.
Пусть t
достаточно мало (близко к нулю). Рассмотрим уравнение линии уровня целевой
функции
Р = (6295
– 14,3t)х1 +
(1560 – 3,3 t)х2 = h.
При малых значениях t
прямая с таким уравнением будет почти параллельна прямой с уравнением Р = 6295 х1 + 1560 х2 = h.
Если «закрепить» линию уровня в т.С и начать увеличивать значение параметра t, то точка Е пересечения
линии уровня с осью Ох2 начнет перемещаться вниз по оси Ох2.
Найдем значение t,
при котором линия уровня параллельна ВС. Из равенства угловых коэффициентов
получаем:
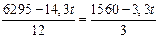 , t =50
, t =50
Следовательно, точка C(540;0) остается точкой
максимума пока tÎ[0;50).
Найдем максимальный размер прибыли для tÎ[0;50):
Р* = (6295
– 14,3t) ´540
+ (1560 – 3,3 t)´0
= 3399300- 7722t (руб.),
Размер необходимого кредита:
V* = 13tx1*
+ 3x2* = 13´t´540 +3´t´0=7020t руб.,
Сумма уплаченных процентов: 0,1V* = 702tруб.
Потребность в трудовых ресурсах: S* = 13x1*
+ 3x2*
= 13´540 +3´0
= 7020(чел.-час.).
Если t=50, то
оптимальное решение будет достигаться на отрезке ВС, концы которого имеют
координаты В(360;720) и C(540;0).
Если «закрепить» линию уровня в т.С и начать увеличивать значение параметра t, то линия уровня будет
приближаться к оси 0х1.
Найдем значение t,
при котором линия уровня параллельна АВ. Из равенства угловых коэффициентов
получаем:
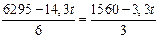 ; t =
412,3 > 60.
; t =
412,3 > 60.
Если tÎ[50;
60] точкой максимума станет точка В с координатами х1* = 360, х2*= 720.
Найдем максимальный размер прибыли для tÎ[0;50):
Р* = (6295
– 14,3t) ´360
+ (1560 – 3,3 t)´720
= 3389400- 7524t
(руб.),
Размер необходимого кредита:
V* = 13tx1* +
3tx2* = 13´10´360 + 3´10´720 =68400 руб.,
Сумма уплаченных процентов: 0,1V* = 0,1´ 68400= 6840руб.
Потребность в
трудовых ресурсах: S* =
13x1* +3
x2*
= 6840(чел.-час.).
Итоги решения задачи представим
в таблице:
|
Почасовая
оплата труда t (руб.)
|
Оптималь-ный
план выпуска Х*(t)= (x1*,x2*)
|
Величина
спроса на трудовые ресурсы S*(t)
(чел.-час.)
|
Размер
необходимого кредита V*(t), (руб.)
|
Величина
максимальной прибыли Р*(t)
(руб.)
|
|
t = 10
|
(360;720)
|
7020
|
70200
|
3322080
|
|
tÎ(10;50)
|
(360;720)
|
7020
|
7020t
|
3399300-
7722t
|
|
t = 50
|
Отрезок ВС
|
[6840; 7020]
|
[342000;351000]
|
3013200
|
|
tÎ(50;60]
|
(540;0)
|
6840
|
6840t
|
3389400-
7524t
|
Задача 3.
Фирма при производстве продукции использует два вида ресурсов: рабочую
силу (L, тыс. чел.-час.) и оборудование (K, тыс. ст.-час.). Производственная
функция (ПФ) фирмы, построенная путем обработки статистических данных, имеет
вид:
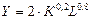 ,
,
где Y — объем выпуска продукции (ед.).
Требуется:
1. Построить графики ПФ при фиксированном значении одной
из переменных: а) K = 90; б) L = 45.
2. Найти уравнения изоквант ПФ и построить их графики
для Y1=69, Y2 = 103, Y3=138.
3. Известны
объем выпуска продукции Y= 103 и наличные трудовые ресурсы L=45 в
базовом периоде. Определить потребность в оборудовании в плановом периоде при
увеличении объема выпуска продукции на 10%, если возможность увеличения
трудовых ресурсов составляет не более 5%.
4. Рабочая
сила нанимается по контракту с почасовой оплатой труда 800 (ден.ед./тыс. чел.-час),
оборудование берется в аренду с суммарными затратами 100 (ден.ед./тыс.
ст.-час). Объем капитала, который фирма может затратить на рабочую силу и
оборудование, составляет 50000 (ден. ед.). Построить математическую модель
задачи оптимизации выпуска продукции, считая, что ПФ задана на всем множестве K ≥ 0, L ≥ 0; найти графическим методом ее решение. Определить
предельную норму технологического замещения оборудования рабочей силой и
предельную эффективность финансовых ресурсов в точке оптимума.
Решаем задачу для следующих значений
параметров:
|
А
|
α
|
β
|
К
|
L
|
Y1
|
Y2
|
Y3
|
Lбаз
|
Yбаз
|
pK
|
pL
|
С
|
|
2
|
0,2
|
0,8
|
90
|
45
|
69
|
103
|
138
|
45
|
103
|
100
|
800
|
50000
|
1) Производственная
функция (ПФ) — функция,
описывающая зависимость максимального объема производимого продукта от затрат
ресурсов (факторов), используемых в производственном процессе. В данной задаче
в качестве ресурсов выступают рабочая сила (L, тыс.
чел.-час.) и оборудование (K, тыс. ст.-час.).
Производственная функция фирмы, построенная путем обработки статистических
данных, имеет вид:
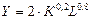
где Y — объем выпуска продукции (ед.).
Построим графики производственной функции при
фиксированном значении одной из переменных.
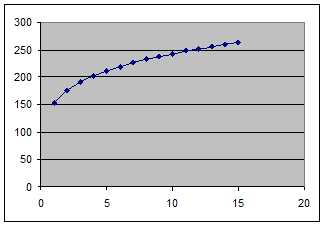
а) По условию K =90. Тогда ПФ — степенная функция следующего вида:
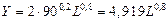
График функции представлен на рис.
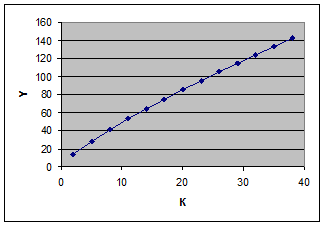
б) По условию L = 45. Тогда ПФ — степенная функция следующего вида:
Y =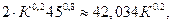
График функции представлен на рис.
2) Изокванта
— совокупность всех комбинаций факторов производства (K, L), обеспечивающих одинаковый
объем выпускаемой продукции. Изокванты дают графическое представление
двухфакторной производственной функции Y(K, L) в виде ее линий уровня.
По условию Y1 =69;Y2 =103; Y3
=138.
Выпишем соответствующие этим
значениям уравнения изоквант:
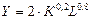 =69;
=69;
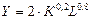 =103;
=103;
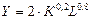 =138.
=138.
Для
построения на декартовой плоскости OKL изоквант из их уравнений в явном виде выразим переменную
L как
функцию от переменной K:
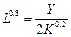 или
или 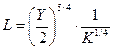 .
.
Итак,
уравнения трех изоквант запишем в следующем виде:
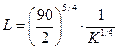 , отсюда
, отсюда 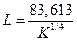 ;
;
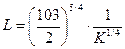 , отсюда
, отсюда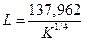 ;
;
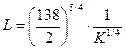 , отсюда.
, отсюда. 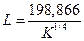
Графики
изоквант, выпуклые к началу координат кривые, изображены на рис. Различные
комбинации (K1, L1) и (K2, L2) используемых ресурсов, принадлежащие одной и той же
изокванте, дают один и тот же объем выпуска Y. Изокванта Y3,
расположенная выше изоквант Y2 и Y1, соответствует большему объему выпуска
продукции (Y3 > Y2 > Y1).
3) Известны объем выпуска продукции Yбаз =
103 (ед.) и наличные трудовые ресурсы Lбаз =45 (тыс. чел.-час.) в базовом периоде. Определим
потребность в оборудовании в плановом периоде при увеличении объема выпуска
продукции на 10%, если возможность увеличения трудовых ресурсов составляет не
более 5%.
При
заданном увеличении объем выпуска продукции составит
Y = 1.1×Yбаз = 1.1×103
= 113,3 (ед.).
Существует
множество комбинаций факторов производства (K, L), обеспечивающих выпуск
продукции в объеме 113,3 ед. Потребность
в оборудовании в плановом периоде можно выразить как функцию от объема трудовых
ресурсов. Используя уравнение изокванты
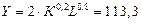 ,
,
имеем:
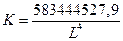 .
.
Таким образом, если объем трудовых ресурсов,
используемых в производстве, не изменится и останется на уровне Lбаз =45
(тыс.чел.-час.), то потребность в оборудовании в плановом периоде составит
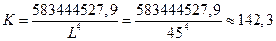 (тыс. ст.-час.).
(тыс. ст.-час.).
В базовом периоде потребность в оборудовании
составляла
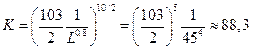 (тыс. ст.-час.).
(тыс. ст.-час.).
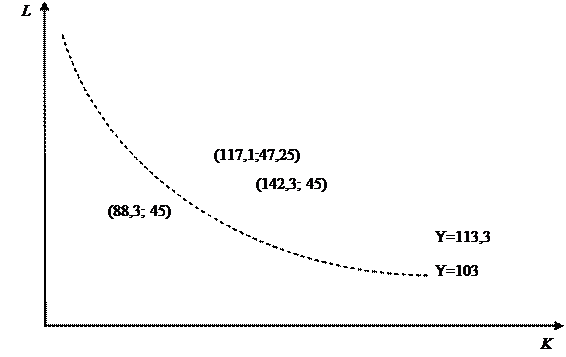
 Потребность
в ресурсах в плановом
Потребность
в ресурсах в плановом



периоде:
Если же объем трудовых ресурсов увеличится на 5% по
отношению к базовому и составит
L = 1.05×Lбаз= 1.05×45
= 47,25 (тыс. чел.-час.),
то потребность в оборудовании в плановом периоде составит
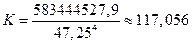 (тыс. ст.-час.).
(тыс. ст.-час.).
Итак, при
объеме трудовых ресурсов 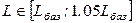 потребность в
оборудовании в плановом периоде составит некоторую величину
потребность в
оборудовании в плановом периоде составит некоторую величину 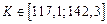 , определяемую соотношением
, определяемую соотношением
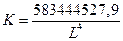 .
.
4) Согласно условию фирма может приобрести на рынке
используемые в производстве ресурсы по ценам pK = 100 (ден. ед.
/ тыс. ст.-час.) и pL
= 800 (ден. ед. / тыс.
чел.-час.). Величина ее затрат C на покупку L единиц рабочей силы и К единиц оборудования
составит
С = pKК + pLL = 100К + 800L.
Задача фирмы состоит в нахождении максимального объема выпуска
продукции при условии, что уровень затрат на покупку ресурсов не превосходит 50000
ден. ед. Математическая модель этой
задачи может быть записана так:
найти объемы ресурсов К и L, удовлетворяющие ограничениям
100К
+ 800L ≤
50000, (1)
К
≥ 0, L ≥ 0 (2)
и доставляющие максимальное значение целевой функции
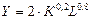 → max. (3)
→ max. (3)
Так как Y —
нелинейная функция, то эта модель представляет собой задачу нелинейного
программирования. Ограничение (1) называется бюджетным ограничением.
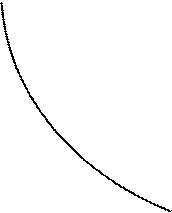
Графическое решение задачи производителя
Ее решение можно найти графическим методом. Для этого
построим область допустимых решений, задаваемую условиями (1) и (2). Она
представляет собой заштрихованный треугольник ОАВ. Граничная прямая АВ
бюджетного ограничения задается уравнением
100K + 800L = 50000
Для определения оптимального решения проведем
несколько линий уровня (изоквант) целевой функции, имеющих общие точки с
областью допустимых решений. Как было показано в п. 2, чем выше находится
изокванта, тем большему уровню целевой функции она соответствует (Y2 > Y1).
Поэтому изокванта, соответствующая максимально возможному объему выпуска,
должна касаться граничной прямой бюджетного ограничения (1), а точка ее касания
D будет оптимальным решением задачи.
Для
нахождения значений координат точки D
используем тот факт, что градиент целевой функции grad Y = 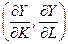 , вычисленный в точке касания, перпендикулярен прямой АВ. Это
означает, что вектор grad Y и вектор нормали ОС = (pK, pL) этой прямой пропорциональны, т.е. справедливо
равенство
, вычисленный в точке касания, перпендикулярен прямой АВ. Это
означает, что вектор grad Y и вектор нормали ОС = (pK, pL) этой прямой пропорциональны, т.е. справедливо
равенство
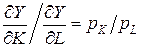 . (4)
. (4)
Поскольку 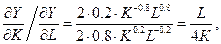 отсюда имеем, что
отсюда имеем, что
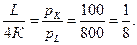
Следовательно, K = 2L.
Подставляя полученное выражение K
через L в уравнение граничной прямой
АВ, получаем:
800L + 100*2L = 50000.
Отсюда
имеем, что оптимальная величина трудовых ресурсов равна
L* = 50.
Оптимальный
объем оборудования равен
K* = 2*L = 2*50 = 100,
а
соответствующий объем выпуска Y* = 2∙1000.2∙500.8
≈ 114,7.
Предельная норма технологического замещения оборудования рабочей
силой в точке рыночного равновесия равна отношению цен этих ресурсов,
т.е.
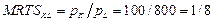 .
.
Предельная эффективность финансовых ресурсов
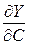 =
= 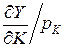 = (0.2∙2∙100-0.8∙500.8)/100
≈ 0.002,
= (0.2∙2∙100-0.8∙500.8)/100
≈ 0.002,
что означает следующее: при увеличении затрат на 1 ден. ед. объем
выпускаемой продукции возрастет на 0.002 ед.
Итак,
получены следующие результаты.
1.
Фирма должна
взять в аренду K* = 100 тыс. ст.-час. оборудования и нанять
по контракту L* = 50 тыс. чел.-час. рабочей силы. В этом случае
при имеющемся бюджетном ограничении будет выпущено максимальное количество
продукции Y* = 114,7 ед.
2.
Предельная норма
технологического замещения оборудования рабочей силой MRTSKL = 1/8.
3.
Предельная
эффективность финансовых ресурсов равна 0.002.
Задача 4
Фирма может влиять дополнительным финансированием на
скорость строительства своего торгового павильона. Очередность выполнения
работ, их нормальная и ускоренная продолжительность выполнения, а также
стоимость строительно-монтажных работ при нормальном и ускоренном режиме
выполнения приведены в следующей таблице:
|
Имя работы
|
А
|
В
|
С
|
D
|
E
|
F
|
G
|
H
|
Q
|
V
|
|
Опирается на работу
|
E,H
|
G,Q
|
V
|
C,A
|
|
E,H
|
|
G,Q
|
V
|
|
|
Нормальный срок
|
4
|
12
|
12
|
4
|
12
|
8
|
11
|
4
|
9
|
4
|
|
Ускоренный срок
|
3
|
9
|
9
|
3
|
9
|
6
|
6
|
3
|
3
|
3
|
|
Норм.стоим.(млн.руб.)
|
6,3
|
50,4
|
26,1
|
6,6
|
22,5
|
40,8
|
42,6
|
22,2
|
23,1
|
24
|
|
Плата за ускор.(млн.руб.)
|
2,3
|
16,8
|
8,7
|
2,2
|
7,5
|
13,6
|
35,5
|
7,4
|
46,2
|
8
|
Требуется:
1.
С учетом технологической последовательности работ
построить сетевой график выполнения этих работ.
2.
Рассчитать временные характеристики сетевого графика
при нормальном режиме выполнения работ. Найти критический путь и его
продолжительность, указать все возможные критические пути, определить стоимость
всего комплекса работ.
3.
Указать стратегию минимального удорожания комплекса
работ при сокращении сроков строительства на 2 дн. С какую итоговую сумму
обойдется фирме ускоренная стройка павильона.
Решение.
Упорядоченный
сетевой график строительства торговой павильона изображен на рис., где
рядом с буквой, обозначающей работу, в скобках проставлено число, равное
нормальному сроку ее выполнения.
Обозначим
Ткр – критическое время, т.е.
наименьшее время выполнения всего комплекса работ.
Трi
– раннее время наступления i-й
события, т.е. момент времени, раньше которого событие i не может наступить.
Рассчитаем Трi
для всех событий сетевого графика, т.е. для i= 1,2,…,6. Время наступления 1-го события сетевого графика будем
считать равным нулю, т.е. Тр1 = 0. Далее последовательно
находим Тр2,…, Тр6
Тр2 = 4 дн
Тр3
=max{Tp2 +t23;t13} = 13дн;
Тр4
=max{Tp3 +tн34; t14} =17 дн;
Тр5
=max{Tp2 +tн25; Тр4+tв45} =
21 дн;
Тр6
=max{ Tp3 +tн36; Tp4 +tн46; Тр5+tв56} =
25дн.
Стоимость S = 6,9+50,4+26,1+6,6+22,5+40,8+42,6+22,2+23,1+24=
264,6
Критический
срок Ткр = 25 дн
Критические
пути (V,Q,H,F), (V,Q,H,А,D), (V,Q,B)
Сокращение сроков строительства торгового
павильона
|
Работы
|
А
|
В
|
С
|
D
|
E
|
F
|
G
|
H
|
Q
|
V
|
|
Норм.прод.
|
4
|
12
|
12
|
4
|
12
|
8
|
11
|
4
|
9
|
4
|
|
Ускор.
|
3
|
9
|
9
|
3
|
9
|
6
|
6
|
3
|
3
|
3
|
|
Норм.цена
|
6,3
|
50,4
|
26,1
|
6,6
|
22,5
|
40,8
|
42,6
|
22,2
|
23,1
|
24
|
|
Плата за ускор.
|
2,3
|
16,8
|
8,7
|
2,2
|
7,5
|
13,6
|
35,5
|
7,4
|
46,2
|
8
|
|
Максим.сокращение времени
выпонения (дн.)
|
1
|
3
|
3
|
1
|
3
|
2
|
5
|
1
|
6
|
1
|
|
Удельн.цена
|
2,3
|
5,6
|
2,9
|
2,2
|
2,5
|
6,8
|
7,1
|
7,4
|
7,7
|
8
|




Просматривая
все полные некритические пути, убеждаемся, что при сокращении срока строительства на 2 дня, т.е. до 23 дней,
критическими могут стать пути Р2, Р3, Р4, Р5,
Р6 и Р7. Необходимо
сократить пути Р2, Р3, Р4 на 2 дня. Все пути
содержат общие работы V
и Q. Cокращаем работу Q
на 2 дня. При этом дополнительные затраты составят:
2(дня) ´ 7,7(млн.руб./день) = 15,4(млн.руб.)
критическое
время станет равным Ткр = 25 –2 =23
(дня)
Новая стоимость
работ будет равной S = 264,6 + 15,4 = 280(млн.руб.)
Задача 5
Имеются данные по 15 субъектам Российской Федерации за январь-март
2001 года о денежных доходах и потребительских расходах на душу населения в
среднем за месяц, которые приведены в
таблице:
|
Номер
субъекта РФ
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Денежные
доходы, тыс.руб.
|
1,57
|
1,58
|
1,75
|
1,46
|
1,91
|
1,79
|
1,33
|
1,58
|
|
Потребительские
расходы, тыс.руб
|
1,11
|
0,87
|
1,3
|
1,36
|
1,51
|
1,19
|
1,08
|
1,28
|
|
Номер
субъекта РФ
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
Денежные
доходы, тыс.руб.
|
2,24
|
1,99
|
2,29
|
2,07
|
2,01
|
3,51
|
1,91
|
|
|
Потребительские
расходы, тыс.руб
|
1,65
|
1,28
|
1,7
|
1,5
|
1,38
|
2,22
|
1,76
|
|
На основе имеющихся данных требуется:
1. Построить поле рассеяния наблюдаемых значений показателей и на
основе его визуального наблюдения выдвинуть гипотезу о виде статистической
зависимости потребительских расходов у от денежных доходов х; записать эту
гипотезу в виде математической модели.
2. Используя метод наименьших квадратов найти точечные оценки
неизвестных параметров модели, записать найденное уравнение регрессии и
построить график функции регрессии.
3. Найти коэффициент парной корреляции между денежными доходами и
потребительскими расходами; проверить его значимость.
4. Найти точечный и интервальный прогноз среднемесячных
потребительских расходов в 10-ом субъекте РФ увеличится на 30%.
5. Привести содержательную интерпретацию полученных результатов.
Решение.
5.1. Построение
математической модели. Оценка неизвестных параметров методом наименьших
квадратов.
Полем рассеяния называется множество точек на плоскости, координаты
которых соответствуют наблюдаемым значениям исследуемых показателей. В нашем
примере хi –
среднедушевые денежные доходы, yi
– среднедушевые потребительские расходы в i-м субъекте РФ, i
= 1,…,15. Таким образом, поле рассеяния состоит из 15-ти точек с координатами (xi,yi), которые
показаны на рис.
Визуальный анализ поля рассеяния позволяет выдвинуть гипотезу о
линейной зависимости потребительских
расходов у от денежных доходов х и записать эту зависимость в виде линейной
модели
у = α + βх + u,
где α, β - неизвестные постоянные коэффициенты, а u – случайная величина,
характеризующая отклонения реальных
значений потребительских расходов от их теоретических значений α +
βх. Случайная величина u
называется случайным отклонением или
случайным возмущением модели. Ее включение в модель призвано отразить:
а) влияние не учтенных в модели факторов, влияющих на размер
потребительских расходов;
б) элемент случайности и непредсказуемости человеческих реакций;
в) ошибки наблюдений и измерений.

5.2 После формулировки
математической модели основная задача состоит в получении оценок неизвестных
параметров α и β по
результатам наблюдений над переменными х и у, т.е. задача состоит в получении
так называемого уравнения регрессии у = a + bх,
являющегося некоторой реализацией модели, в котором коэффициенты а и b есть оценки неизвестных
параметров α и β соответственно. Оценки а и b можно искать по следующим формулам:
nΣxiyi – ΣxiΣyi
b = ———————
, а = уср - bхср.
nΣxi2
– (Σxi)2
Для удобства вычисления оценок искомых коэффициентов модели
составляется табл.1, в которой столбцы
«у», «у - у», «(у - у)2» заполняются после нахождения
уравнения регрессии.
Табл.1
|
Номер субъекта РФ
|
х
|
у
|
х2
|
ху
|
у2
|
ŷ
|
ŷ-у
|
(ŷ-у)2
|
|
1
|
1,57
|
1,11
|
2,465
|
1,743
|
1,232
|
1,213
|
0,103
|
0,011
|
|
2
|
1,58
|
0,87
|
2,496
|
1,375
|
0,757
|
1,219
|
0,349
|
0,122
|
|
3
|
1,75
|
1,30
|
3,063
|
2,275
|
1,690
|
1,312
|
0,012
|
0,000
|
|
4
|
1,46
|
1,36
|
2,132
|
1,986
|
1,850
|
1,153
|
-0,207
|
0,043
|
|
5
|
1,91
|
1,51
|
3,648
|
2,884
|
2,280
|
1,400
|
-0,110
|
0,012
|
|
6
|
1,79
|
1,19
|
3,204
|
2,130
|
1,416
|
1,334
|
0,144
|
0,021
|
|
7
|
1,33
|
1,08
|
1,769
|
1,436
|
1,166
|
1,081
|
0,001
|
0,000
|
|
8
|
1,58
|
1,28
|
2,496
|
2,022
|
1,638
|
1,219
|
-0,061
|
0,004
|
|
9
|
2,24
|
1,65
|
5,018
|
3,696
|
2,723
|
1,582
|
-0,068
|
0,005
|
|
10
|
1,99
|
1,28
|
3,960
|
2,547
|
1,638
|
1,444
|
0,164
|
0,027
|
|
11
|
2,29
|
1,70
|
5,244
|
3,893
|
2,890
|
1,609
|
-0,091
|
0,008
|
|
12
|
2,07
|
1,50
|
4,285
|
3,105
|
2,250
|
1,488
|
-0,012
|
0,000
|
|
13
|
2,01
|
1,38
|
4,040
|
2,774
|
1,904
|
1,455
|
0,075
|
0,006
|
|
14
|
3,51
|
2,22
|
12,320
|
7,792
|
4,928
|
2,280
|
0,060
|
0,004
|
|
15
|
1,91
|
1,76
|
3,648
|
3,362
|
3,098
|
1,400
|
-0,360
|
0,129
|
|
cymm
|
28,99
|
21,19
|
59,788
|
43,020
|
31,461
|
21,190
|
0,000
|
0,391
|
Находим оценки а и b.
Получаем:
хср = Σхi/15 =28,99/15
= 1,933 (тыс.руб.) – среднее значение среднедушевых доходов;
уср = Σуi/15 = 21,19/15 = 1,413 (тыс.руб.) – среднее значение
среднедушевых потребительских расходов.
Следовательно, b = 0,55
а = уср – bxcp = 0,35
Таким образом, искомое уравнение регрессии примет вид
ŷ = 0,55x + 0,35
Найденное уравнение регрессии есть уравнение прямой, которая
изображена на рис.
5.3. Нахождение
коэффициента корреляции.
Мерой зависимости между переменными х и у может служить выборочный
коэффициент парной корреляции, который обозначается через rxy и определяется по формуле:
nΣxiyi
– ΣxiΣyi
rxy
= ——————¾¾¾¾——¾— ,
√nΣxi2
– (Σxi)2 √ nΣуi2 – (Σуi)2
Подставляя соответствующие значения из
последней строки табл.1, получаем
rxy
= 0,863, rxy
> 0 и близко к 1, следовательно, связъ сильная положительная, т.е. при
увеличении доходов, расходы растут.
Для того, чтобы с большей уверенностью делать
вывод о наличии или отсутствии линейной взаимосвязи между переменными х и у,
разработан критерий проверки того, существенно ли отличие коэффициента
корреляции от нуля или, другими словами, значимо ли значение коэффициента
корреляции. Если в результате проверки выясняется, что коэффициент корреляции
существенно отличается от нуля, то, несмотря даже на не очень близкое значение
коэффициента к единице, делается вывод о наличии линейной взаимосвязи между
переменными х и у. Если же подтверждается несущественное отличие rxy от
нуля, то, не смотря на возможно достаточно большое значение коэффициента,
делается вывод об отсутствии линейной взаимосвязи между переменными.
Проверка существенности отличия коэффициента
корреляции от нуля проводится по схеме: .
│ rxy √ n-2
│
если │ ¾¾¾¾ │ > t1-α/2,n-2 ,
√1 – rxy2
то гипотеза о существенном отличии коэффициента корреляции от нуля
принимается, в противном случае отвергается.
Здесь t1-α/2,n-2 – квантиль
распределения Стьюдента, α -
уровень значимости или уровень доверия, n – число наблюдений, (n-2) – число степеней свободы. Значение
α задается исследователем зависимости между х и у. Примем α = 0,05,
тогда t1-α/2,n-2 = t0,975,13 = 2,1604
.
rxy √ n-2 0,863´√15-2
¾¾¾¾ = ¾¾¾¾¾ = 6,147
> t0,975,13
√1 – rxy2 √1- 0,8632
Следовательно, коэффициент корреляции существенно отличается от нуля и
существует сильная линейная связь между х и у. Т.е. если мы будем проводить многократное
повторение эксперимента по исследованию зависимости между доходами и расходами,
всякий раз выбирая различные группы из 15 субъектов РФ, то в 95% этих
экспериментов будет обнаружена тесная линейная зависимость между х и у, т.е.
в 95% случаев коэффициент корреляции rxy будет
существенно отличатся от нуля.
5.4 Нахождение точечных и интервальных прогнозов.
Точечным прогнозом значения зависимой переменной у,
соответствующего некоторому значению независимой переменной х = х0,
называется значение ŷ0, получаемое путем подстановки в
уравнение регрессии х = х0, т.е.
ŷ0 = ŷ(х0)= a + bx0 – точечный прогноз.
Найдем точечный прогноз среднемесячных
потребительских расходов в 10-ом субъекте РФ в будущем периоде, что
среденемесячные денежные доходы в этом субъекте
увеличатся на 30%, т.е.
х0 = х10 + 0,3´х10 = 1,3´х10 = 1,3´1,99
= 2,587
ŷ0 = 0,35 + 0,55´2,587
= 1.772 (тыс.руб.).
Таким образом, если среднемесячные денежные доходы в
10-м субъекте РФ увеличатся на 30%, то
потребительские расходы в этом субъекте составят 1.772 тыс.руб.
Интервальным прогнозом зависимой переменной у,
соответствующим некоторому значению независимой переменной х = х0,
называется доверительный интервал, границы которого находятся по формуле:
ŷв.н. = ŷ(х0) ± t1-α/2,n-2Sŷ,
где ув, ун – соответственно
верхняя и нижняя границы доверительного интервала;
ŷ(х0) – точечный прогноз;
t1-α/2,n-2 –квантиль
распределения Стьюдента;
(1-α/2) – доверительная вероятность;
(n-2)
– число степеней свободы;
/
1 (x0 – xcp) S(ŷi - yi)2
Sŷ = S √
¾
+ ¾¾¾¾¾ ,
S = √S2 , S2 = ¾¾¾¾,
n S(xi – xcp)2 n-2
Доверительный интервал – это такой интервал, в
котором с заданной вероятностью будет находиться прогнозируемое значение
зависимой переменной у.
Найдем интервальный прогноз среднемесячных
потребительских расходов в 10-м субъекте РФ в будущем периоде предполагая, что
среднемесячные денежные доходы в этом субъекте
РФ увеличатся на 30%.
Ранее вычислено ожидаемое значение денежных доходов
х0 = 2,587 тыс.руб.
Пусть α = 0,05, тогда 1-α = 0,95; t1-α/2,n-2 = t0,975,13
= 2,1604;
S(ŷi - yi)2 0,391 .
S2
= ¾¾¾¾ = ¾¾¾ = 0,03; S = √ 0.03 = 0.173
n – 2 13
(х0 - хср)2 =
(2,587 – 1,933)2 = 0,428
S(xi - xcp)2 =
Sхi2 – n(xcp)2 = 59,788- 15´1,9332
= 3,76.
_______________ ____________
/ 1
(x0 – xcp)2 / 1 0,428
Sŷ = S √
¾
+ ¾¾¾¾¾
= 0.173 √ ¾
+ ¾¾¾¾
= 0,074
n S(xi – xcp)2 15 3,76
Следовательно, ŷн =1.772 – 0,074 =
1,698 (тыс.руб.)
ŷв
= 1.772 + 0,074 = 1,846(тыс.руб.)
Это означает , что при увеличении среднедушевых
среднемесячных денежных доходов на 30%, т.е. с 1,99 тыс.руб. до 2,587 тыс.руб.,
размер среднедушевых среднемесячных потребительских расходов с вероятностью 0,95 будет колебаться в
пределах от 1,698 тыс.руб. до1,846 тыс.руб.
5.5
Содержательная интерпретация полученных результатов.
Рассмотрим найденное уравнение регрессии ŷ =0,55x
+ 0,35. Коэффициент а = 0,35 не имеет экономического смысла, поскольку
формально соответствует размеру потребительских расходов при нулевом уровне
денежных доходов. Коэффициент b
= 0,55 определяет прирост
потребительских расходов, обусловленный приростом денежных доходов.
Содержательная интерпретация всех остальных понятий
и формул, использованных в данной задаче была приведена по ходу решения.
В заключение впишем итоговые результаты.
1.
у = α + βх + u – математическая модель зависимости
потребительских расходов от денежных доходов.
2.
ŷ =0,55x + 0,35– уравнение регрессии,
количественно выражающее зависимость расходов от доходов.
3.
rxy
=0,863– коэффициент корреляции между х и у, его значение свидетельствует о
достаточно тесной линейной зависимости расходов и доходов.
4. ŷ0 (х0)
= 1.772 (тыс.руб.) – точечный прогноз;
ŷн = 1,698 (тыс.руб.)
ŷв = 1,846
(тыс.руб.) - интервальный прогноз с 95% доверительной вероятностью.