СОДЕРЖАНИЕ
Введение. 3
1. Типы и виды статистических наблюдений. 5
2. Понятие о выборочном методе. 7
2.1. Основы выборочного метода. 7
2.2. Логика выборочного наблюдения. 8
3. Ошибки выборки. 9
3. Порядок планирования расходов на
образовательные учреждения. 15
4. Способы отбора единиц из генеральной
совокупности. 15
Заключение. 19
Практическая часть. 20
Задание 1. 20
Задание 2. 24
Задание 3. 25
Задание 4. 30
Задание 5. 31
Список литературы.. 34
Введение
Статистика имеет многовековую
историю. Её возникновение и развитие обусловлены общественными потребностями:
подсчет населения, скота, учета земельных угодий, имущества и т.д. Наиболее
ранние сведения о таких работах в Китае относятся к 13 в. до нашей эры. В
Древнем Риме проводились учеты свободных граждан и их имущества.
Считается, что основы
статистической науки заложены английским экономистом У. Петти (1623-1687)г. Он
рассматривал статистику как науку об управлении. В 1746г. немецкий профессор
философии и права Ахенваль впервые в Марбургском университете начал читать
новую дисциплину, названную им статистикой.
В развитии статистики
видное место принадлежит представителям отечественной науки и практики. В эпоху
Петра I статистика трактовалась преимущественно как описательная наука. Но уже
со второй половины XIX в. выдвигается познавательное значение статистики.
Профессор петербургского университета Ю.Э. Янсон (1835-93) назвал статистику
общественной наукой. Видный экономист А.И. Чупров (1842-1908) отмечал
необходимость массового статистического исследования при помощи метода
количественного наблюдения большого числа факторов для того, чтобы описать
общественные явления, подметить законы и определить причины, их вызвавшие.
Развитие статистики в России тесным образом связано с созданной после отмены
крепостного права земской статистикой, которая пользовалась заслуженным
авторитетом за объективность и профессионализм.
История развития
статистики показывает, что статистическая наука сложилась в результате
теоретического обобщения накопленного человечеством передового опыта
учетно-статистических работ, обусловленных, прежде всего, потребностями
управления жизни общества.
Целью данной работы
является подробное изучение одного из основных понятий статистики – выборочного
наблюдения, а именно видов выборки, ошибок выборки, оптимальной численности
выборки, способов распространения характеристик выборки на генеральную
совокупность, способы отбора единиц их генеральной совокупности.
Так же автор работы
преследовал цель закрепить полученные теоретические знания при решении 5
практических заданий.
1. Типы и виды статистических наблюдений
Статистическое
наблюдение — это
начальная стадия экономико-статистического наблюдения. Она представляет собой
научно организационную работу по собиранию массовых первичных данных о явлениях
и процессах общественной жизни [2, c. 20-23].
Любое статистическое
наблюдение осуществляется с помощью оценки и регистрации признаков единиц
совокупности в соответствующих учетных документах. Таким образом, полученные
данные представляют собой факты, которые так или иначе характеризуют явления
общественной жизни.
Статистическое наблюдение
должно отвечать следующим требованиям.
1. Наблюдаемые явления
должны иметь научную и практическую ценность, выражать определенные
социально-экономические типы явлений.
2. Непосредственный сбор
массовых данных должен обеспечить полноту фактов, относящихся к
рассматриваемому вопросу, так как явления находятся в постоянном изменении,
развитии. В том случае, если отсутствуют полные данные, анализ и выводы могут
быть ошибочными.
3. Для обеспечения
достоверности статистических данных необходима тщательная всесторонняя проверка
(контроль) качества собираемых фактов.
4. Для того, чтобы
создать наилучшие условия для получения объективных материалов, необходима
научная организация статистического наблюдения.
Статистическое наблюдение
осуществляется в двух формах: путём предоставления отчётности и проведения
специально организованных статистических наблюдений.
Отчётностью называют такую организованную форму
статистического наблюдения, при которой сведения поступают в виде обязательных
отчётов в определённые сроки и по утверждённым формам.
При этом источником
сведений, как правило, являются первичные учётные записи в документах
бухгалтерского и оперативного учёта.
Специально организованное
статистическое наблюдение представляет собой сбор сведений посредством
переписей, единовременных учётов и обследований. Примером специально
организованного статистического наблюдения могут быть: перепись населения,
всякого рода социологические обследования, переписи промышленного оборудования,
остатки материалов и другие переписи в промышленности, в сельском хозяйстве,
строительстве, на транспорте, в торговле и т.д.
Виды статистического
наблюдения различаются по времени регистрации данных и по степени охвата единиц
исследуемой совокупности.
По характеру регистрации
данных во времени различают наблюдение непрерывное, или текущее, и прерывное
(периодическое). Последнее, в свою очередь подразделяется на наблюдение
периодическое и наблюдение единовременное.
Текущим (непрерывным) является такое
наблюдение, которое ведётся систематически. При этом регистрация фактов
производится по мере их свершения, например, регистрация актов гражданского
состояния, учёт произведённой продукции, отпуска материалов со склада, выручки
магазинов. При текущем наблюдении нельзя допускать значительного разрыва между
моментом возникновения факта и моментом его регистрации.
Прерывным (периодическим) является такое
наблюдение, которое повторяется через определённые промежутки времени.
Например, ежегодные переписи скота, проводимые по состоянию на 1 января.
Единовременное (разовое) наблюдение проводится по
мере надобности, время от времени, без соблюдения строгой периодичности или
вообще проводится единожды. Примером могут служить социально-экономические
выборочные обследования, проводимые Научно-исследовательским институтом по
изучению спроса на товары народного потребления и конъюнктуры торговли.
По степени охвата единиц
изучаемой совокупности различают сплошные и несплошные статистические
наблюдения.
Сплошным называют такое наблюдение, при
котором обследованию подвергаются все без исключения единицы изучаемой
совокупности. Примером сплошного наблюдения может служить Всесоюзная перепись
населения. Путем сплошного наблюдения осуществляется получение отчетности от
предприятий и учреждений.
Несплошным называют такое наблюдение, при
котором обследованию подвергаются не все единицы изучаемой совокупности, а
только заранее установленная их часть, например, изучение торговых оборотов и
цен на городских рынках. Основным видом несплошного наблюдения является
выборочное. Выборочным наблюдением
называется наблюдение, при котором характеристика всей совокупности фактов
дается по некоторой их части, отобранной в случайном порядке. В промышленности
его используют для контроля качества продукции, в сельском хозяйстве — при
выявлении продуктивности скота, в контрольных проверках — при переписи скота и
других работах. В торговле с его помощью изучают эффективность новых, передовых
форм торговли, спрос населения и степень его удовлетворения. Постоянно
проводятся выборочные обследования бюджетов семей рабочих, служащих и
колхозников и т.д.
2. Понятие о выборочном методе
2.1. Основы выборочного метода
Выборочное наблюдение –
одно из наиболее современных видов статистического наблюдения. Выборочное
наблюдение – это такое наблюдение, при котором обследованию подвергается часть
единиц изучаемой совокупности, отобранных на основе научно разработанных
принципов, обеспечивающих получение достаточного количества достоверных данных,
для того чтобы охарактеризовать всю совокупность в целом [1, c. 11-15].
Средние и относительные
показатели, полученные на основе выборочных данных, должны достаточно полно
воспроизводить или репрезентатировать соответствующие показатели совокупности в
целом.
2.2. Логика выборочного наблюдения
(1)
определение
объекта и целей выборочного наблюдения;
(2)
выбор
схема отбора единиц для наблюдения;
(3)
расчет
объема выборки;
(4)
проведение
случайного отбора установленного числа единиц из генеральной совокупности;
(5)
наблюдение
отобранных единиц по установленной программе;
(6)
расчет
выборочных характеристик в соответствии с программой выборочного наблюдения;
(7)
определение
ошибки, ее размера;
(8)
распространение
выборочных данных на генеральную совокупность;
(9)
анализ
полученных данных.
Основные преимущества
(1)
Выборочное
наблюдение можно осуществить по более широкой программе.
(2)
Выборочное
наблюдение более дешевое с точки зрения затрат на его проведение.
(3)
Выборочное
наблюдение можно организовать тогда и в тех случаях, когда отчетностью мы
воспользоваться не можем.
Основные недостатки
(1)
Полученные
данные всегда содержат в себе ошибку, о результатах наблюдения можно судить
лишь с определенной степенью достоверности. Но по сравнению с другими видами
наблюдения это достоинство выборочного метода.
(2)
Для
его проведения требуются квалифицированные кадры.
Вся совокупность единиц,
из которых производится отбор, называется генеральной. Совокупность единиц
отобранных называется выборочной.
3. Ошибки выборки
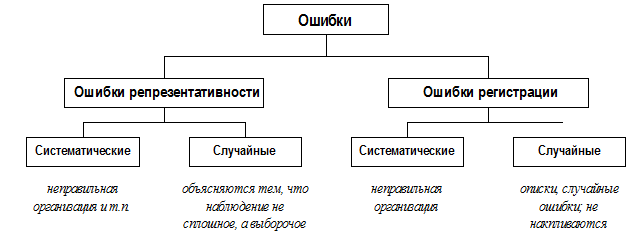 Чтобы оценить степень точности
выборочного наблюдения, необходимо оценить величину ошибок, которые могут
возникнуть в процессе проведения выборочного наблюдения [1, c. 17-21].
Чтобы оценить степень точности
выборочного наблюдения, необходимо оценить величину ошибок, которые могут
возникнуть в процессе проведения выборочного наблюдения [1, c. 17-21].
Основное внимание уделяется случайным
ошибкам репрезентативности.
Выборочное наблюдение.
Статистическое
исследование может осуществляться по данным несплошного наблюдения, основная
цель которого состоит в получении характеристик изучаемой совокупности по
обследованной ее части. Одним из наиболее распространенных в статистике методов,
применяющих несплошное наблюдение, является выборочный метод.
Под выборочным понимается
метод статистического исследования, при котором обобщающие показатели изучаемой
совокупности устанавливаются по некоторой ее части на основе положений случайного
отбора. При выборочном методе обследованию подвергается сравнительно небольшая
часть всей изучаемой совокупности (обычно до 5 — 10%, реже до 15 — 25%). При
этом подлежащая изучению статистическая совокупность, из которой производится
отбор части единиц, называется генеральной совокупностью. Отобранная из
генеральной совокупности некоторая часть единиц, подвергающаяся обследованию,
называется выборочной совокупностью или просто выборкой.
Значение выборочного
метода состоит в том, что при
минимальной численности обследуемых единиц проведение исследования
осуществляется в более короткие сроки и с минимальными затратами труда и
средств. Это повышает оперативность статистической информации, уменьшает ошибки
регистрации.
В проведении ряда
исследований выборочный метод является единственно возможным, например, при
контроле качества продукции (товара), если проверка сопровождается уничтожением
или разложением на составные части обследуемых образцов (определение сахаристости
фруктов, клейковины печеного хлеба, установление носкости обуви, прочности
тканей на разрыв и т.д.).
Проведение исследования
социально — экономических явлений выборочным методом складывается из ряда
последовательных этапов:
1) обоснование (в
соответствии с задачами исследования) целесообразности применения выборочного метода;
2) составление программы
проведения статистического исследования выборочным методом;
3) решение
организационных вопросов сбора и обработки исходной информации;
4) установление доли
выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;
5) обоснование способов
формирования выборочной совокупности;
6) осуществление отбора
единиц из генеральной совокупности для их обследования;
7) фиксация в отобранных
единицах (пробах) изучаемых признаков;
8) статистическая
обработка полученной в выборке информации с определением обобщающих характеристик
изучаемых признаков;
9) определение
количественной оценки ошибки выборки;
10) распространение
обобщающих выборочных характеристик на генеральную совокупность.
В генеральной
совокупности доля единиц, обладающих изучаемым признаком, называется генеральной
долей (обозначается р), а средняя величина изучаемого варьирующего признака
— генеральной средней (обозначается 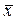 ).
).
В выборочной совокупности
долю изучаемого признака называют выборочной долей, или частостью (обозначается
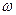 ), а среднюю величину
в выборке — выборочной средней (обозначается
), а среднюю величину
в выборке — выборочной средней (обозначается 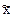 ).
).
Пример [4, c.22].
При контрольной проверке
качества хлебобулочных изделий проведено 5%-ное выборочное обследование партии
нарезных батонов из муки высшего сорта. При этом из 100 отобранных в выборку
батонов 90 шт. соответствовали требованиям стандарта. Средний вес одного батона
в выборке составлял 500,5 г при среднем квадратическом отклонении 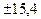 г.
г.
На основе полученных в
выборке данных нужно установить возможные значения доли стандартных изделий и
среднего веса одного изделия во всей партии.
Прежде всего
устанавливаются характеристики выборочной совокупности. Выборочная доля, или
частость, 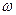 определяется из
отношения единиц, обладающих изучаемым признаком m, к общей численности единиц
выборочной совокупности n:
определяется из
отношения единиц, обладающих изучаемым признаком m, к общей численности единиц
выборочной совокупности n:
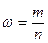
Поскольку из 100 изделий,
попавших в выборку n, 90 ед. оказались стандартными m, то показатель частости
равен: 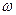 = 90:100=0,9.
= 90:100=0,9.
Средний вес изделия в
выборке х = 500,5 г определен взвешиванием. Но полученные показатели частости
(0,9) и средней величины (500,5 г) характеризуют долю стандартной продукции и
средний вес одного изделия лишь в выборке. Для определения соответствующих
показателей для всей партии товара надо установить возможные при этом значения
ошибки выборки.
Ошибка выборки — это объективно возникающее
расхождение между характеристиками выборки и генеральной совокупности. Она
зависит от ряда факторов: степени вариации изучаемого признака, численности
выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности
результата исследования.
Определение ошибки
выборочной средней.
При случайном повторном
отборе средняя ошибка выборочной средней рассчитывается по формуле:
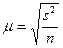 ,
,
 где
где
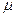 — средняя ошибка
выборочной средней;
— средняя ошибка
выборочной средней;
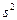 — дисперсия выборочной совокупности;
— дисперсия выборочной совокупности;
n — численность выборки.
При бесповторном отборе
она рассчитывается по формуле:
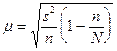 ,
,
где N — численность
генеральной совокупности.
Определение ошибки
выборочной доли.
При повторном отборе
средняя ошибка выборочной доли рассчитывается по формуле:


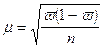 ,
,
где 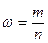 — выборочная доля единиц, обладающих изучаемым признаком;
— выборочная доля единиц, обладающих изучаемым признаком;
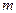 — число единиц,
обладающих изучаемым признаком;
— число единиц,
обладающих изучаемым признаком;
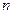 — численность выборки.
— численность выборки.
При бесповторном способе
отбора средняя ошибка выборочной доли определяется по формулам:
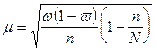
Предельная ошибка
выборки 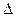 связана со средней ошибкой выборки
связана со средней ошибкой выборки 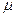 отношением:
отношением:
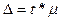 .
.
При этом t как
коэффициент кратности средней ошибки выборки зависит от значения вероятности Р,
с которой гарантируется величина предельной ошибки выборки.
Предельная ошибка выборки
при бесповторном отборе определяется по следующим формулам:
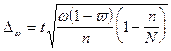 ,
,
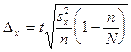 .
.
Предельная ошибка выборки
при повторном отборе определяется по формуле:
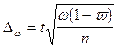 ,
,
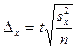 .
.
Малая выборка.
При контроле качества
товаров в экономических исследованиях эксперимент может проводиться на основе
малой выборки.
Под малой выборкой
понимается несплошное статистическое обследование, при котором выборочная
совокупность образуется из сравнительно небольшого числа единиц генеральной
совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить
до 4 — 5 единиц.
Средняя ошибка малой
выборки 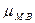 вычисляется по
формуле:
вычисляется по
формуле:
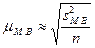 ,
,
где 
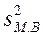 — дисперсия малой
выборки.
— дисперсия малой
выборки.
При определении дисперсии
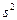 число степеней свободы
равно n-1:
число степеней свободы
равно n-1:
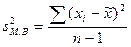 .
.
Предельная ошибка малой
выборки 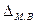 определяется по
формуле
определяется по
формуле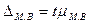
При этом значение
коэффициента доверия t зависит не только от заданной доверительной вероятности,
но и от численности единиц выборки n. Для отдельных значений t и n доверительная
вероятность малой выборки определяется по специальным таблицам Стьюдента (Табл.
9.1.), в которых даны распределения стандартизированных отклонений:
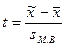 .
.
Поскольку при проведении
малой выборки в качестве доверительной вероятности практически принимается
значение 0,59 или 0,99, то для определения предельной ошибки малой выборки 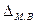 используются следующие
показания распределения Стьюдента:
используются следующие
показания распределения Стьюдента:
|
n
|
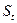
|
|
|
0,95
|
0,99
|
|
4
|
3,183
|
5,841
|
|
5
|
2,777
|
4,604
|
|
6
|
2,571
|
4,032
|
|
7
|
2,447
|
3,707
|
|
8
|
2,364
|
3,500
|
|
9
|
2,307
|
3,356
|
|
10
|
2,263
|
3,250
|
|
15
|
2,119
|
2,921
|
|
20
|
2,078
|
2,832
|
3. Порядок планирования расходов на образовательные
учреждения
Способы
распространения характеристик выборки на генеральную совокупность [2, c.54].
Выборочный метод чаще
всего применяется для получения характеристик генеральной совокупности по
соответствующим показателям выборки. В зависимости от целей исследований это
осуществляется или прямым пересчётом показателей выборки для генеральной
совокупности, или посредством расчёта поправочных коэффициентов.
Способ прямого
пересчёта. Он
состоит в том, что показатели выборочной доли 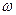 или средней
или средней 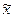 распространяется на
генеральную совокупность с учётом ошибки выборки.
распространяется на
генеральную совокупность с учётом ошибки выборки.
Так, в торговле
определяется количество поступивших в партии товара нестандартных изделий. Для
этого (с учётом принятой степени вероятности) показатели доли нестандартных
изделий в выборке умножаются на численность изделий во всей партии товара.
Способ поправочных
коэффициентов.
Применяется в случаях, когда целью выборочного метода является уточнение
результатов сплошного учета.
В статистической практике
этот способ используется при уточнении данных ежегодных переписей скота,
находящегося у населения. Для этого после обобщения данных сплошного учета
практикуется 10%-ное выборочное обследование с определением так называемого
“процента недоучета”.
4. Способы отбора единиц из генеральной
совокупности
В статистике применяются
различные способы формирования выборочных совокупностей, что обусловливается
задачами исследования и зависит от специфики объекта изучения [5, c. 122].
Основным условием
проведения выборочного обследования является предупреждение возникновения систематических
ошибок, возникающих вследствие нарушения принципа равных возможностей попадания
в выборку каждой единицы генеральной совокупности. Предупреждение
систематических ошибок достигается в результате применения научно обоснованных
способов формирования выборочной совокупности.
Существуют следующие
способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор —
в выборку отбираются отдельные единицы;
2) групповой отбор — в
выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор
— это комбинация индивидуального и группового отбора.
Способы отбора
определяются правилами формирования выборочной совокупности.
Выборка может быть:
— собственно-случайная;
— механическая;
— типическая;
— серийная;
— комбинированная.
Собственно-случайная
выборка состоит в
том, что выборочная совокупность образуется в результате случайного
(непреднамеренного) отбора отдельных единиц из генеральной совокупности. При
этом количество отобранных в выборочную совокупность единиц обычно определяется
исходя из принятой доли выборки.
Доля выборки есть
отношение числа единиц выборочной совокупности n к численности единиц генеральной
совокупности N, т.е.
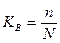 .
.
Так, при 5%-ной выборке
из партии товара в 2 000 ед. численность выборки n составляет 100 ед.
(5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д.
Механическая выборка состоит в том, что отбор единиц в
выборочную совокупность производится из генеральной совокупности, разбитой на
равные интервалы (группы). При этом размер интервала в генеральной совокупности
равен обратной величине доли выборки.
Так, при 2%-ной выборке
отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я
единица (1:0,05) и т.д.
Таким образом, в
соответствии с принятой долей отбора, генеральная совокупность как бы
механически разбивается на равновеликие группы. Из каждой группы в выборку
отбирается лишь одна единица.
Важной особенностью
механической выборки является то, что формирование выборочной совокупности
можно осуществить, не прибегая к составлению списков. На практике часто
используют тот порядок, в котором фактически размещаются единицы генеральной
совокупности. Например, последовательность выхода готовых изделий с конвейера
или поточной линии, порядок размещения единиц партии товара при хранении,
транспортировке, реализации и т.д.
Типическая выборка. При типической выборке генеральная
совокупность вначале расчленяется на однородные типические группы. Затем из
каждой типической группы собственно-случайной или механической выборкой
производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно
применяется при изучении сложных статистических совокупностей. Например, при
выборочном обследовании производительности труда работников торговли, состоящих
из отдельных групп по квалификации.
Важной особенностью
типической выборки является то, что она дает более точные результаты по сравнению
с другими способами отбора единиц в выборочную совокупность.
Для определения средней
ошибки типической выборки используются формулы:
повторный
отбор
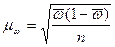 ,
, 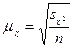
бесповторный
отбор
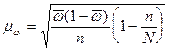 ,
, 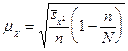
Дисперсия определяется по
следующим формулам:
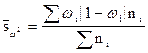 ,
, 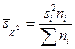
При одноступенчатой
выборке каждая отобранная единица сразу же подвергается изучению по заданному
признаку. Так обстоит дело при собственно-случайной и серийной выборке.
При многоступенчатой
выборке производят подбор из генеральной совокупности отдельных групп, а из
групп выбираются отдельные единицы. Так производится типическая выборка с
механическим способом отбора единиц в выборочную совокупность.
Комбинированная выборка может быть двухступенчатой.
При этом генеральная совокупность сначала разбивается на группы. Затем
производят отбор групп, а внутри последних осуществляется отбор отдельных
единиц.
Заключение
В статистической практике
применяются различные виды несплошного
наблюдения: выборочное, способ основного массива, анкетное и
монографическое. Качество несплошного наблюдения уступает результатам
сплошного, однако вполне очевидны и некоторые преимущества первого: выигрыш во
времени для принятия оперативного решения, а также соблюдение режима экономии
ресурсов. В ряде случаев статистическое наблюдение вообще оказывается возможным
только как несплошное. Оно используется для получения представительной характеристики
всей совокупности по некоторой части ее единиц применяют выборочное наблюдение.
В промышленности выборочное наблюдение применяется при статистическом контроле
качества продукции, изучении использования производственного оборудования,
рабочего места станочников и т.д.
В теоретической части мы
рассмотрели основные понятия выборочного наблюдения, полученные знания
необходимо закрепить на практике, путем решения практических задач.
Практическая
часть
Задание 1
Для выявления зависимости
между экономическими показателями деятельности фирм провести группировку
показателей 50 аудиторских фирм (Таблица 1). Группировку провести с равными
интервалами, выделив 4-5 групп.
Результативным признаком
является балансовая прибыль.
Группировочный признак – оплата труда.
Таблица 1
|
№
п/п
|
Выручка
от реализации, руб.
|
Балансовая
прибыль, руб.
|
Численность
работников, чел.
|
Основные
средства, руб.
|
Нематериальные
активы, руб.
|
Оплата
труда, руб.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
8
|
13256
|
71
|
1
|
2592
|
0
|
0
|
|
9
|
10083
|
40
|
3
|
0
|
31
|
2284
|
|
10
|
90902
|
37416
|
8
|
0
|
7438
|
42230
|
|
11
|
140000
|
4100
|
7
|
3075
|
0
|
16000
|
|
12
|
12847
|
1116
|
1
|
14322
|
6375
|
98
|
|
13
|
0
|
0
|
1
|
0
|
1067
|
0
|
|
14
|
56500
|
4957
|
5
|
0
|
0
|
2376
|
|
15
|
30841
|
9838
|
5
|
4820
|
10631
|
14595
|
|
16
|
35274
|
632
|
6
|
0
|
406
|
10777
|
|
17
|
45520
|
14453
|
2
|
20442
|
3100
|
2742
|
|
18
|
93578
|
50890
|
15
|
5166
|
2419
|
18336
|
|
19
|
53234
|
32117
|
11
|
7164
|
5746
|
8679
|
|
20
|
83278
|
24541
|
43
|
9580
|
7428
|
22485
|
|
21
|
56119
|
3244
|
12
|
7166
|
5846
|
14679
|
|
22
|
47360
|
2870
|
9
|
0
|
19665
|
4140
|
|
23
|
45914
|
11309
|
2
|
0
|
7752
|
3729
|
|
24
|
122502
|
38654
|
38
|
21600
|
15755
|
72650
|
|
25
|
142683
|
48400
|
45
|
27992
|
20431
|
70698
|
|
26
|
68849
|
19120
|
14
|
8493
|
10356
|
32600
|
|
27
|
67580
|
15545
|
16
|
11400
|
9300
|
30110
|
|
28
|
15980
|
7400
|
4
|
2600
|
4735
|
6536
|
|
29
|
11307
|
6372
|
2
|
3500
|
3800
|
4995
|
|
30
|
12238
|
8100
|
3
|
4800
|
5136
|
6300
|
|
31
|
83761
|
20950
|
15
|
23480
|
17210
|
43930
|
|
32
|
81235
|
37133
|
13
|
25590
|
19700
|
44000
|
|
33
|
85320
|
31500
|
17
|
18650
|
20600
|
36500
|
|
34
|
94638
|
36100
|
35
|
24380
|
17840
|
57180
|
|
35
|
59187
|
1200
|
21
|
15200
|
11457
|
34170
|
|
36
|
61328
|
500
|
23
|
12950
|
13400
|
29420
|
|
37
|
40155
|
19148
|
10
|
8460
|
8100
|
19725
|
|
38
|
44333
|
13200
|
11
|
13596
|
7939
|
18880
|
Таблица 1 (Продолжение)
|
№
п/п
|
Выручка
от реализации, руб.
|
Балансовая
прибыль, руб.
|
Численность
работников, чел.
|
Основные
средства, руб.
|
Нематериальные
активы, руб.
|
Оплата
труда, руб.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
40
|
39490
|
12500
|
8
|
7920
|
6532
|
20400
|
|
41
|
60125
|
18451
|
9
|
10432
|
11470
|
25808
|
|
42
|
63100
|
5600
|
13
|
9830
|
24586
|
36486
|
|
43
|
72354
|
12735
|
24
|
16900
|
21258
|
48132
|
|
44
|
77995
|
10540
|
27
|
15782
|
18726
|
57489
|
|
45
|
87486
|
30900
|
28
|
14890
|
23775
|
29560
|
|
46
|
98640
|
40000
|
30
|
12800
|
17160
|
48700
|
|
47
|
25811
|
6541
|
7
|
5420
|
4170
|
14109
|
|
48
|
27415
|
8900
|
8
|
4656
|
3560
|
15788
|
|
49
|
32645
|
2156
|
6
|
7000
|
6500
|
25690
|
|
50
|
120800
|
45820
|
36
|
26100
|
25120
|
60120
|
|
51
|
19654
|
550
|
3
|
2810
|
1500
|
10200
|
|
52
|
21700
|
3450
|
4
|
4580
|
3750
|
12700
|
|
53
|
14932
|
6114
|
3
|
3296
|
3600
|
7815
|
|
54
|
13399
|
2777
|
1
|
4010
|
5020
|
5920
|
|
55
|
12957
|
130
|
2
|
2600
|
186
|
6250
|
|
56
|
17639
|
1445
|
3
|
4521
|
4807
|
10600
|
|
57
|
21500
|
3512
|
6
|
5012
|
5498
|
11000
|
Необходимо так же
рассчитать коэффициенты вариации по группировочному признаку на основании
исходных данных и по аналитической группировке, согласно своему варианту.
Объяснить расхождения в значениях полученных коэффициентов.
Решение
1)
Рассчитаем
коэффициент вариации по группировочному признаку на основании исходных данных:
Коэффициент вариации равен
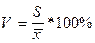 ,
,
где S - среднее квадратическое отклонение,
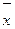 - средняя арифметическая взвешенная
- средняя арифметическая взвешенная
В свою очередь среднее квадратическое
отклонение определяется:
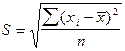 ,
,
где 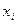 - значения вариант
выборки,
- значения вариант
выборки,
n – размер выборки.
Средняя арифметическая
рассчитывается:
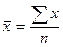
Рассчитаем среднюю арифметическую по
группировочному признаку (оплата труда, см. таблицу 1):
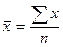 =
= 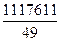 =22808.39
(руб.)
=22808.39
(руб.)
Среднее квадратическое отклонение:
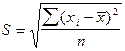 =19323,29
=19323,29
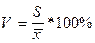 =
= 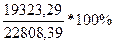 = 84,7%
= 84,7%
Коэффициент вариации по группировочному признаку V=84,7%
2)
Рассчитаем
коэффициент вариации по аналитической группировке. Для этого необходимо сначала
сгруппировать выборку по признаку «оплата труда».
Шаг группировочого признака равен
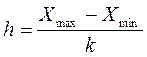 , где k- количество групп,
, где k- количество групп, 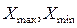 - максимальное и минимальное значение
группировочного признака
- максимальное и минимальное значение
группировочного признака
h = 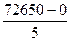 = 14530
(руб.)
= 14530
(руб.)
Результат группировки представлен в
таблице 2.
Таблица 2
|
|
Балансовая
прибыль, руб.
|
|
№группы
|
1
|
2
|
3
|
4
|
5
|
|
Оплата труда, руб
|
0 - 14530
|
14531 - 29060
|
29061 - 43591
|
43592 - 58122
|
58123 - 72650
|
|
1
|
71
|
4100
|
37416
|
20950
|
38654
|
|
2
|
40
|
9838
|
19120
|
37133
|
48400
|
|
3
|
1116
|
50890
|
15545
|
36100
|
45820
|
|
4
|
0
|
24541
|
31500
|
12735
|
|
|
5
|
4957
|
3244
|
1200
|
10540
|
|
|
6
|
632
|
19148
|
500
|
40000
|
|
|
7
|
14453
|
13200
|
5600
|
|
|
|
8
|
32117
|
12500
|
30900
|
|
|
|
9
|
2870
|
18451
|
|
|
|
|
10
|
11309
|
8900
|
|
|
|
|
11
|
7400
|
2156
|
|
|
|
|
12
|
6372
|
|
|
|
|
|
13
|
8100
|
|
|
|
|
|
14
|
6541
|
|
|
|
|
|
15
|
550
|
|
|
|
|
|
16
|
3450
|
|
|
|
|
|
17
|
6114
|
|
|
|
|
|
18
|
2777
|
|
|
|
|
|
19
|
130
|
|
|
|
|
|
20
|
1445
|
|
|
|
|
|
21
|
3512
|
|
|
|
|
Рассчитаем коэффициенты вариации по
каждой из групп:
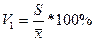 =
=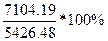 =130.9%
=130.9%
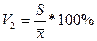 =
=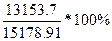 =86.7%
=86.7%
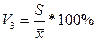 =
=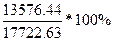 =76.6 %
=76.6 %
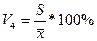 =
=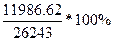 =45.7%
=45.7%
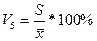 =
=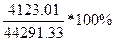 =9.3%
=9.3%
Мы получили 5 коэффициентов вариации
(по каждой из групп). Их расхождения между собой, а так же между ними и
коэффициентом вариации по группировочному признаку можно объяснить связью между
группировочным и результативным признаками (то есть оплата труда влияет на
балансовую прибыль).
Задание 2
Провести 30% механическую
выборку из генеральной совокупности, представленной в таблице 1, по показателю
«балансовая прибыль». С вероятностью 0,95 рассчитать границы изменения средней
величины в генеральной совокупности и сравнить с результатом, полученным на
основании расчета по выборочной совокупности.
Решение
Проведем 30% выборку из
генеральной совокупности, то есть выберем каждую 3-ю единицу. Результат
приведен в таблице 3.
Таблица 3
|
№ п/п
|
Выручка от реализации, руб.
|
Балансовая прибыль, руб.
|
Численность работников, чел.
|
Основные средства, руб.
|
Нематериальные активы, руб.
|
Оплата труда, руб.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
10
|
90902
|
37416
|
8
|
0
|
7438
|
42230
|
|
13
|
0
|
0
|
1
|
0
|
1067
|
0
|
|
16
|
35274
|
632
|
6
|
0
|
406
|
10777
|
|
19
|
53234
|
32117
|
11
|
7164
|
5746
|
8679
|
|
22
|
47360
|
2870
|
9
|
0
|
19665
|
4140
|
|
25
|
142683
|
48400
|
45
|
27992
|
20431
|
70698
|
|
28
|
15980
|
7400
|
4
|
2600
|
4735
|
6536
|
|
31
|
83761
|
20950
|
15
|
23480
|
17210
|
43930
|
|
34
|
94638
|
36100
|
35
|
24380
|
17840
|
57180
|
|
37
|
40155
|
19148
|
10
|
8460
|
8100
|
19725
|
|
41
|
60125
|
18451
|
9
|
10432
|
11470
|
25808
|
|
44
|
77995
|
10540
|
27
|
15782
|
18726
|
57489
|
|
47
|
25811
|
6541
|
7
|
5420
|
4170
|
14109
|
|
50
|
120800
|
45820
|
36
|
26100
|
25120
|
60120
|
|
53
|
14932
|
6114
|
3
|
3296
|
3600
|
7815
|
|
56
|
17639
|
1445
|
3
|
4521
|
4807
|
10600
|
|
59
|
87453
|
20957
|
11
|
20400
|
14680
|
51330
|
Границы изменения средней
величины, то есть предельная ошибка выборки 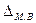 определяется по
формуле
определяется по
формуле
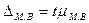 ,
,
Средняя ошибка малой выборки 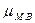 вычисляется по
формуле:
вычисляется по
формуле:
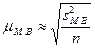 ,
,
где 
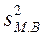 — дисперсия малой
выборки.
— дисперсия малой
выборки.
В нашем случае значение
коэффициента доверия t=0,95.
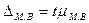 =0,95*3922.75=3726.61
=0,95*3922.75=3726.61
Границы изменения средней
величины балансовой прибыли 14796.98 – 22250.2 (руб)
Задание 3
По данным Таблицы 4 рассчитать:
1)
среднегодовой
ввод жилых домов;
2)
базисные,
цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов
прироста ввода жилых домов;
3)
изобразить
динамику ввода жилых домов на графике.
Таблица 4
|
Год
|
Введено жилых домов, тыс м2
общей площади
|
|
1988
|
37
|
|
1989
|
42
|
|
1990
|
46
|
|
1991
|
48
|
|
1992
|
48
|
|
1993
|
50
|
|
1994
|
50
|
|
1995
|
51
|
|
1996
|
52
|
|
1997
|
52
|
Решение
1) Среднегодовой ввод жилых домов 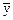 равен
равен
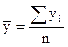 =
=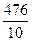 =47,6 (тыс м2)
=47,6 (тыс м2)
2) Рассчитаем базисные, цепные и
среднегодовые темпы роста ввода жилых домов.
2.1 Цепной темп роста - каждый уровень ряда сопоставляется
с предшествующим ему уровнем: 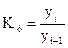 ,
,
Базисный - все уровни ряда
сопоставляются с одним и тем же уровнем 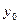 , выбранным за базу сравнения:
, выбранным за базу сравнения: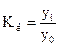 .
.
Результаты расчета представлены в
таблице 5 и на рисунках 1 и 2.
Таблица 5
|
Год
|
Введено жилых домов, тыс м2
общей площади
|
Темп роста цепн
|
Темп роста баз
|
|
1988
|
37
|
|
|
|
1989
|
42
|
1.14
|
1.14
|
|
1990
|
46
|
1.10
|
1.24
|
|
1991
|
48
|
1.04
|
1.30
|
|
1992
|
48
|
1
|
1.30
|
|
1993
|
50
|
1.04
|
1.35
|
|
1994
|
50
|
1
|
1.35
|
|
1995
|
51
|
1.02
|
1.38
|
|
1996
|
52
|
1.02
|
1.41
|
|
1997
|
52
|
1
|
1.41
|
Среднегодовой цепной показатель темпа
роста – 0,94
Среднегодовой базисный показатель
темпа роста – 1,19
Рисунок 1
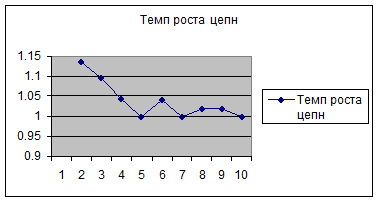
Рисунок 2
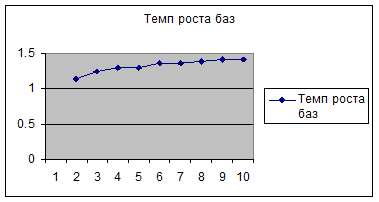
2.2. Показатель абсолютного прироста
Цепной абсолютный прирост - 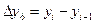 ;
;
Базисный абсолютный прирост - 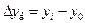 .
.
Результаты расчета приведены в таблице 6 и на рисунках
3,4.
Таблица 6
|
Год
|
Введено жилых домов, тыс м2
общей площади
|
Абсолютный прирост, цепн
|
Абсолютный прирост, баз
|
|
1988
|
37
|
|
|
|
1989
|
42
|
5
|
5
|
|
1990
|
46
|
4
|
9
|
|
1991
|
48
|
2
|
11
|
|
1992
|
48
|
0
|
11
|
|
1993
|
50
|
2
|
13
|
|
1994
|
50
|
0
|
13
|
|
1995
|
51
|
1
|
14
|
|
1996
|
52
|
1
|
15
|
|
1997
|
52
|
0
|
15
|
Среднегодовой цепной
показатель абсолютного прироста – 1,5
Среднегодовой
базисный показатель абсолютного прироста – 10,6
Рисунок 3

Рисунок 4
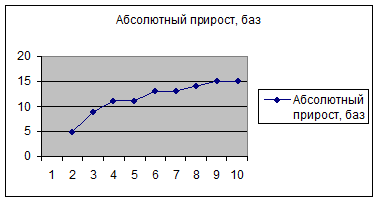
2.3. Показатель темпов прироста
Базисные темпы прироста: 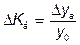
 .
.
Цепные темпы прироста: 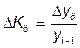 .
.
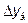 и
и 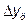 - абсолютный базисный или цепной прирост;
- абсолютный базисный или цепной прирост;
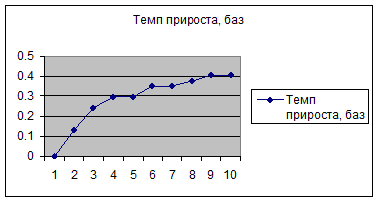
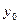 - уровень ряда динамики,
выбранный за базу для определения базисных абсолютных приростов;
- уровень ряда динамики,
выбранный за базу для определения базисных абсолютных приростов;
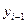 - уровень ряда
динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
- уровень ряда
динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
Результаты расчета приведены в
таблице 7 и на рисунках 5 и 6.
Таблица 7
|
Год
|
Введено жилых домов, тыс м2
общей площади
|
Темп прироста, цепн
|
Темп прироста, баз
|
|
1988
|
37
|
0
|
0
|
|
1989
|
42
|
0.12
|
0.14
|
|
1990
|
46
|
0.09
|
0.24
|
|
1991
|
48
|
0.04
|
0.30
|
|
1992
|
48
|
0
|
0.30
|
|
1993
|
50
|
0.04
|
0.35
|
|
1994
|
50
|
0
|
0.35
|
|
1995
|
51
|
0.02
|
0.38
|
|
1996
|
52
|
0.02
|
0.41
|
|
1997
|
52
|
0
|
0.41
|
Среднегодовой цепной
показатель темпов прироста – 0,03
Среднегодовой
базисный показатель темпов прироста – 0,29
Рисунок 5
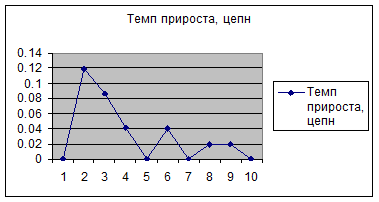
Рисунок 6
Задание 4
По данным таблицы 8
определить:
1)
Общие
индексы:
А) цен;
Б) физического объема
проданных товаров;
В) товарооборота.
Какую роль в изменении
товарооборота сыграли изменения цен и количества проданных товаров?
2)
Абсолютную
величину изменения расходов населения, происшедшего в связи с изменением цен.
Таблица 8
|
Вид товара
|
Предыдущий период
|
Отчетный период
|
|
Кол-во, шт
|
Цена за ед., руб
|
Кол-во, шт
|
Цена за ед., руб
|
|
Тазы
|
80
|
55
|
60
|
90
|
|
Раковины
|
20
|
240
|
25
|
250
|
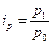 Решение
Решение
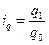 1) Общий индекс цен рассчитывается
1) Общий индекс цен рассчитывается
Общий индекс объема
проданных товаров
Первый период принимается
за базисный, в котором цена единицы товара принимается 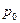 , а количество —
, а количество —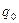 .
.
Второй период принимается
за текущий (или отчетный), в котором цена единицы товара обозначается 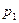 , а количество —
, а количество — 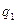 .
.
Общий индекс товарооборота 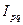 =
=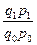
Результаты расчетов приведены в
таблице 9
Таблица 9
|
Вид товара
|
Предыдущий период
|
Отчетный период
|
Общие индексы
|
|
Кол-во, шт
|
Цена за ед., руб
|
Кол-во, шт
|
Цена за ед., руб
|
цен
|
физического объема
|
Товаро-
оборота
|
|
Тазы
|
80
|
55
|
60
|
90
|
1.64
|
0.75
|
1.23
|
|
Раковины
|
20
|
240
|
25
|
250
|
1.04
|
1.25
|
1.30
|
Вывод
Из результатов расчета
можно сделать вывод, что цена на тазы в отчетном периоде по сравнению с
базисным возросла на 64%, цена на раковины – всего на 4%, тогда как спрос на
тазы снизился на 25%, а на раковины возрос на 25%, в целом величина
товарооборота тазов возросла на 23%, раковин – на 30%.
3) Для того, чтобы определить абсолютную
величину расходов населения, происшедшую в связи с изменением цен, необходимо
рассчитать агрегатный индекс изменения расходов населения:
Агрегатная формула такого общего индекса цен имеет
следующий вид:
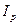 =
=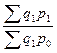
числитель индексного отношения
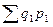 =60*90+ 25 * 250 = 11650 руб.
=60*90+ 25 * 250 = 11650 руб.
знаменатель индексного отношения
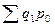 = 60*55+25*240= 9300 руб.
= 60*55+25*240= 9300 руб.
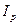 =
=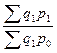 =
=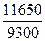 =1,25
=1,25
Абсолютная величина
изменения расходов населения в связи с изменением цен равна +2350 руб.
Задание
5
Для выявления зависимости между
показателями необходимо рассчитать линейный коэффициент корреляции по исходным
данным (Таблица 1).
Решение
Наиболее
удобной формулой для расчета коэффициента корреляции является:
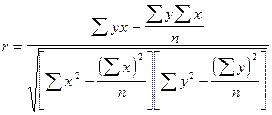
Коэффициент
корреляции можно рассчитать и по другой формуле:
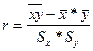 , где
, где
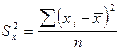 и
и 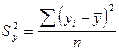
Таблица 10
|
№ п/п
|
Балансовая прибыль, руб. (x)
|
Оплата труда, руб. (y)
|
x2
|
y2
|
xy
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
8
|
71
|
0
|
5041
|
0
|
0
|
|
9
|
40
|
2284
|
1600
|
5216656
|
91360
|
|
10
|
37416
|
42230
|
1399957056
|
1783372900
|
1580077680
|
|
11
|
4100
|
16000
|
16810000
|
256000000
|
65600000
|
|
12
|
1116
|
98
|
1245456
|
9604
|
109368
|
|
13
|
0
|
0
|
0
|
0
|
0
|
|
14
|
4957
|
2376
|
24571849
|
5645376
|
11777832
|
|
15
|
9838
|
14595
|
96786244
|
213014025
|
143585610
|
|
16
|
632
|
10777
|
399424
|
116143729
|
6811064
|
|
17
|
14453
|
2742
|
208889209
|
7518564
|
39630126
|
|
18
|
50890
|
18336
|
2589792100
|
336208896
|
933119040
|
|
19
|
32117
|
8679
|
1031501689
|
75325041
|
278743443
|
|
20
|
24541
|
22485
|
602260681
|
505575225
|
551804385
|
|
21
|
3244
|
14679
|
10523536
|
215473041
|
47618676
|
|
22
|
2870
|
4140
|
8236900
|
17139600
|
11881800
|
|
23
|
11309
|
3729
|
127893481
|
13905441
|
42171261
|
|
24
|
38654
|
72650
|
1494131716
|
5278022500
|
2808213100
|
|
25
|
48400
|
70698
|
2342560000
|
4998207204
|
3421783200
|
|
26
|
19120
|
32600
|
365574400
|
1062760000
|
623312000
|
|
27
|
15545
|
30110
|
241647025
|
906612100
|
468059950
|
|
28
|
7400
|
6536
|
54760000
|
42719296
|
48366400
|
|
29
|
6372
|
4995
|
40602384
|
24950025
|
31828140
|
|
30
|
8100
|
6300
|
65610000
|
39690000
|
51030000
|
|
31
|
20950
|
43930
|
438902500
|
1929844900
|
920333500
|
|
32
|
37133
|
44000
|
1378859689
|
1936000000
|
1633852000
|
|
33
|
31500
|
36500
|
992250000
|
1332250000
|
1149750000
|
|
34
|
36100
|
57180
|
1303210000
|
3269552400
|
2064198000
|
|
35
|
1200
|
34170
|
1440000
|
1167588900
|
41004000
|
|
36
|
500
|
29420
|
250000
|
865536400
|
14710000
|
|
37
|
19148
|
19725
|
366645904
|
389075625
|
377694300
|
|
38
|
13200
|
18880
|
174240000
|
356454400
|
249216000
|
|
40
|
12500
|
20400
|
156250000
|
416160000
|
255000000
|
|
41
|
18451
|
25808
|
340439401
|
666052864
|
476183408
|
|
42
|
5600
|
36486
|
31360000
|
1331228196
|
204321600
|
|
43
|
12735
|
48132
|
162180225
|
2316689424
|
612961020
|
|
44
|
10540
|
57489
|
111091600
|
3304985121
|
605934060
|
|
45
|
30900
|
29560
|
954810000
|
873793600
|
913404000
|
|
46
|
40000
|
48700
|
1600000000
|
2371690000
|
1948000000
|
|
47
|
6541
|
14109
|
42784681
|
199063881
|
92286969
|
|
48
|
8900
|
15788
|
79210000
|
249260944
|
140513200
|
|
49
|
2156
|
25690
|
4648336
|
659976100
|
55387640
|
|
50
|
45820
|
60120
|
2099472400
|
3614414400
|
2754698400
|
|
51
|
550
|
10200
|
302500
|
104040000
|
5610000
|
|
52
|
3450
|
12700
|
11902500
|
161290000
|
43815000
|
|
53
|
6114
|
7815
|
37380996
|
61074225
|
47780910
|
|
54
|
2777
|
5920
|
7711729
|
35046400
|
16439840
|
|
55
|
130
|
6250
|
16900
|
39062500
|
812500
|
|
56
|
1445
|
10600
|
2088025
|
112360000
|
15317000
|
|
57
|
3512
|
11000
|
12334144
|
121000000
|
38632000
|
|
ИТОГО
|
713037
|
1117611
|
2.1034E+10
|
4.3787E+10
|
2.5843E+10
|
Все
необходимые данные для определения коэффициента корреляции есть в таблице, их
лишь остается подставить в необходимую формулу.
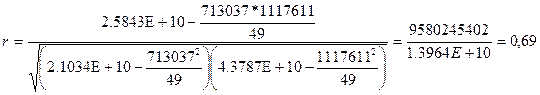
Вывод
Коэффициент корреляции r=0,69, он положительный и по модулю
больше нуля, следовательно, между показателями балансовая прибыль и оплата
труда существует прямая связь.
Список
литературы
1. Общая теория статистики./Под ред.
И.И. Елисеевой. – М.: Финансы и статистика, 2001г.
2. Статистика: Курс лекций./Никитина
Н.Ш. – Новосибирск: НГТУ, 2002г.
3. Айвазян С.А., Енюков И.С., Мешалкин
Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных.
Справочное изд. – М.: Финансы и статистика, 1983.
4. Сборник задач по общей теории
статистики. Учебное пособие. – М.: Финансы и статистика, 1986 г.
5. Общая теория статистики:
Статистическая методология в изучении коммерческой деятельности./ под. ред. А.А.
Спирина, О.Э. Башиной. – М.: Финансы и статистика, 1997 г.