Задание №2 (Вариант 6)
Разработать таблицы
расчета определенного интеграла при разбиении отрезка интегрирования на 10,20,
30 и 40 частей, а также построить диаграмму подынтегральной функции y=f(x).
Исходные данные:
- определить площадь
полосы отвода между км 500 и км 510, которая описывается интегралом:
510
∫ x4/500*(7*x+15* x2+112*
x3) dx
500
- метод определения площади криволинейной трапеции –
метод трапеций.
Расчет площади интеграла при разбиении отрезка на 10
частей:
|
x
|
y
|
|
500
|
0,008926178
|
|
501
|
0,008944035
|
|
502
|
0,008961893
|
|
503
|
0,00897975
|
|
504
|
0,008997607
|
|
505
|
0,009015464
|
|
506
|
0,009033321
|
|
507
|
0,009051178
|
|
508
|
0,009069035
|
|
509
|
0,009086893
|
|
510
|
0,00910475
|
|
S=
|
0,09015464
|
Расчет площади интеграла при разбиении отрезка на 20
частей:
|
x
|
y
|
|
500
|
0,008926178
|
|
500,5
|
0,008935107
|
|
501
|
0,008944035
|
|
501,5
|
0,008952964
|
|
502
|
0,008961893
|
|
502,5
|
0,008970821
|
|
503
|
0,00897975
|
|
503,5
|
0,008988678
|
|
504
|
0,008997607
|
|
504,5
|
0,009006535
|
|
505
|
0,009015464
|
|
505,5
|
0,009024393
|
|
506
|
0,009033321
|
|
506,5
|
0,00904225
|
|
507
|
0,009051178
|
|
507,5
|
0,009060107
|
|
508
|
0,009069035
|
|
508,5
|
0,009077964
|
|
509
|
0,009086893
|
|
509,5
|
0,009095821
|
|
510
|
0,00910475
|
|
S=
|
0,09015464
|
Расчет площади интеграла при разбиении отрезка на 30
частей:
|
x
|
y
|
|
500
|
0,008926178
|
|
500,3333333
|
0,008932131
|
|
500,6666667
|
0,008938083
|
|
501
|
0,008944035
|
|
501,3333333
|
0,008949988
|
|
501,6666667
|
0,00895594
|
|
502
|
0,008961893
|
|
502,3333333
|
0,008967845
|
|
502,6666667
|
0,008973797
|
|
503
|
0,00897975
|
|
503,3333333
|
0,008985702
|
|
503,6666667
|
0,008991654
|
|
504
|
0,008997607
|
|
504,3333333
|
0,009003559
|
|
504,6666667
|
0,009009512
|
|
505
|
0,009015464
|
|
505,3333333
|
0,009021416
|
|
505,6666667
|
0,009027369
|
|
506
|
0,009033321
|
|
506,3333333
|
0,009039274
|
|
506,6666667
|
0,009045226
|
|
507
|
0,009051178
|
|
507,3333333
|
0,009057131
|
|
507,6666667
|
0,009063083
|
|
508
|
0,009069035
|
|
508,3333333
|
0,009074988
|
|
508,6666667
|
0,00908094
|
|
509
|
0,009086893
|
|
509,3333333
|
0,009092845
|
|
509,6666667
|
0,009098797
|
|
510
|
0,00910475
|
|
S=
|
0,09015464
|
Расчет площади интеграла при разбиении отрезка на 40
частей:
|
x
|
y
|
|
500
|
0,008926178
|
|
500,25
|
0,008930643
|
|
500,5
|
0,008935107
|
|
500,75
|
0,008939571
|
|
501
|
0,008944035
|
|
501,25
|
0,0089485
|
|
501,5
|
0,008952964
|
|
501,75
|
0,008957428
|
|
502
|
0,008961893
|
|
502,25
|
0,008966357
|
|
502,5
|
0,008970821
|
|
502,75
|
0,008975285
|
|
503
|
0,00897975
|
|
503,25
|
0,008984214
|
|
503,5
|
0,008988678
|
|
503,75
|
0,008993143
|
|
504
|
0,008997607
|
|
504,25
|
0,009002071
|
|
504,5
|
0,009006535
|
|
504,75
|
0,009011
|
|
505
|
0,009015464
|
|
505,25
|
0,009019928
|
|
505,5
|
0,009024393
|
|
505,75
|
0,009028857
|
|
506
|
0,009033321
|
|
506,25
|
0,009037785
|
|
506,5
|
0,00904225
|
|
506,75
|
0,009046714
|
|
507
|
0,009051178
|
|
507,25
|
0,009055643
|
|
507,5
|
0,009060107
|
|
507,75
|
0,009064571
|
|
508
|
0,009069035
|
|
508,25
|
0,0090735
|
|
508,5
|
0,009077964
|
|
508,75
|
0,009082428
|
|
509
|
0,009086893
|
|
509,25
|
0,009091357
|
|
509,5
|
0,009095821
|
|
509,75
|
0,009100285
|
|
510
|
0,00910475
|
|
S=
|
0,09015464
|
Формулы расчета площади при разбиении
отрезка на 20 частей:
|
x
|
y
|
|
500
|
=СТЕПЕНЬ(D2;4)/(500*(7*D2+15*СТЕПЕНЬ(D2;2)+112*СТЕПЕНЬ(D2;3)))
|
|
=D2+0,5
|
=СТЕПЕНЬ(D3;4)/(500*(7*D3+15*СТЕПЕНЬ(D3;2)+112*СТЕПЕНЬ(D3;3)))
|
|
=D3+0,5
|
=СТЕПЕНЬ(D4;4)/(500*(7*D4+15*СТЕПЕНЬ(D4;2)+112*СТЕПЕНЬ(D4;3)))
|
|
=D4+0,5
|
=СТЕПЕНЬ(D5;4)/(500*(7*D5+15*СТЕПЕНЬ(D5;2)+112*СТЕПЕНЬ(D5;3)))
|
|
=D5+0,5
|
=СТЕПЕНЬ(D6;4)/(500*(7*D6+15*СТЕПЕНЬ(D6;2)+112*СТЕПЕНЬ(D6;3)))
|
|
=D6+0,5
|
=СТЕПЕНЬ(D7;4)/(500*(7*D7+15*СТЕПЕНЬ(D7;2)+112*СТЕПЕНЬ(D7;3)))
|
|
=D7+0,5
|
=СТЕПЕНЬ(D8;4)/(500*(7*D8+15*СТЕПЕНЬ(D8;2)+112*СТЕПЕНЬ(D8;3)))
|
|
=D8+0,5
|
=СТЕПЕНЬ(D9;4)/(500*(7*D9+15*СТЕПЕНЬ(D9;2)+112*СТЕПЕНЬ(D9;3)))
|
|
=D9+0,5
|
=СТЕПЕНЬ(D10;4)/(500*(7*D10+15*СТЕПЕНЬ(D10;2)+112*СТЕПЕНЬ(D10;3)))
|
|
=D10+0,5
|
=СТЕПЕНЬ(D11;4)/(500*(7*D11+15*СТЕПЕНЬ(D11;2)+112*СТЕПЕНЬ(D11;3)))
|
|
=D11+0,5
|
=СТЕПЕНЬ(D12;4)/(500*(7*D12+15*СТЕПЕНЬ(D12;2)+112*СТЕПЕНЬ(D12;3)))
|
|
=D12+0,5
|
=СТЕПЕНЬ(D13;4)/(500*(7*D13+15*СТЕПЕНЬ(D13;2)+112*СТЕПЕНЬ(D13;3)))
|
|
=D13+0,5
|
=СТЕПЕНЬ(D14;4)/(500*(7*D14+15*СТЕПЕНЬ(D14;2)+112*СТЕПЕНЬ(D14;3)))
|
|
=D14+0,5
|
=СТЕПЕНЬ(D15;4)/(500*(7*D15+15*СТЕПЕНЬ(D15;2)+112*СТЕПЕНЬ(D15;3)))
|
|
=D15+0,5
|
=СТЕПЕНЬ(D16;4)/(500*(7*D16+15*СТЕПЕНЬ(D16;2)+112*СТЕПЕНЬ(D16;3)))
|
|
=D16+0,5
|
=СТЕПЕНЬ(D17;4)/(500*(7*D17+15*СТЕПЕНЬ(D17;2)+112*СТЕПЕНЬ(D17;3)))
|
|
=D17+0,5
|
=СТЕПЕНЬ(D18;4)/(500*(7*D18+15*СТЕПЕНЬ(D18;2)+112*СТЕПЕНЬ(D18;3)))
|
|
=D18+0,5
|
=СТЕПЕНЬ(D19;4)/(500*(7*D19+15*СТЕПЕНЬ(D19;2)+112*СТЕПЕНЬ(D19;3)))
|
|
=D19+0,5
|
=СТЕПЕНЬ(D20;4)/(500*(7*D20+15*СТЕПЕНЬ(D20;2)+112*СТЕПЕНЬ(D20;3)))
|
|
=D20+0,5
|
=СТЕПЕНЬ(D21;4)/(500*(7*D21+15*СТЕПЕНЬ(D21;2)+112*СТЕПЕНЬ(D21;3)))
|
|
=D21+0,5
|
=СТЕПЕНЬ(D22;4)/(500*(7*D22+15*СТЕПЕНЬ(D22;2)+112*СТЕПЕНЬ(D22;3)))
|
|
S=
|
=0,5*((E2+E22)/2+СУММ(E3:E21))
|
График
криволинейной границы полосы отвода:
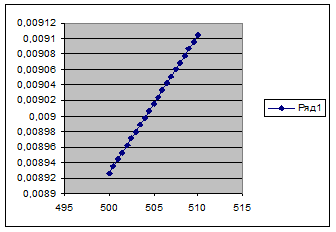
Расчет
точности определения значения интеграла:
∆20= S20-S10= 0,09015464 - 0,09015464 =
7,71605E-15
∆30= S30-S20= 0,09015464 - 0,09015464 =
1,38778E-15
∆40= S40-S30= 0,09015464 - 0,09015464 =
5,41234E-16
Вывод: Метод трапеций имеет высокую
степень точности.