Содержание
3. Что называется вязкостью
жидкости? В чем сущность закона вязкого трения Ньютона?. 3
14. Указать физический смысл величин, входящих в
дифференциальное уравнение Эйлера гидродинамики. 3
23. Особенности течения жидкости в плоских и
цилиндрических зазорах. 4
33. Основные расчетные соотношения при
последовательном и параллельном
соединении труб. 6
Задача 1. 9
Задача 8. 9
Задача 17. 10
Задача 22. 11
Задача 30. 12
Задача 40. 14
Список литературы.. 15
3. Что
называется вязкостью жидкости? В чем сущность закона вязкого трения Ньютона?
Всем реальным жидкостям
присущи вязкость или внутреннее трение, что приводит к появлению у них
принципиально новых свойств. В частности, возникшее в жидкости движение после
прекращения действия причин, его вызвавших, постепенно замедляется.
Следовательно, жидкость при своем движении в трубе испытывает сопротивление.
Такого рода сопротивление называют вязким, подчеркивая тем самым отличие от
сопротивления в твердых телах.
В
соответствии с третьим законом Ньютона силы внутреннего трения равны по
величине и противоположны по направлению, поэтому верхний слой замедляет
движение нижнего, а нижний - ускоряет движение верхнего. Величина силы
внутреннего трения задается формулой Ньютона:
Fтр = η·|Δv/Δz|·S,
где η - коэффициент вязкости;
|Δv/Δz| - модуль градиента скорости, показывающий, как быстро меняется
величина вектора скорости в направлении, перпендикулярном течению
жидкости;
S - площадь поверхности соприкасающихся слоев жидкости.
14.
Указать физический смысл величин, входящих в дифференциальное уравнение Эйлера
гидродинамики
Обязательным условием
покоя жидкости являлось равновесие всех сил. Таким образом равновесие
математически было сформулировано:
Fдавления + Fмассовые = 0
В результате
преобразования этого уравнения для трех направления получили:
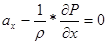 ;
; 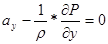 ;
; 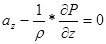
Отличие движущейся
жидкости – возможность ее ускоренного движения. А это значит, что сумма
поверхностных и массовых сил в движущейся жидкости может не быть равно «0».
Fдавления + Fмассовые = r*(du/dt)
Где: u –
скорость движения жидкости;
t - время;
r*(du/dt) – сила инерции.
Учет сил инерции
позволяет получить уравнений движения (уравнений динамического равновесия),
получивших название Уравнения ЭЙЛЕРА
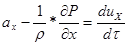 ;
; 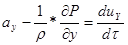 ;
; 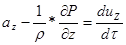
23. Особенности течения жидкости в плоских и
цилиндрических зазорах
В жидкости,
заполняющей скважину, упругая волна может распространяться в пределах
измерительного зонда в кольцевом зазоре между стенкой скважины и скважинным
прибором. Если рассматривать саму скважину и этот кольцевой зазор как столб
жидкости или газа с жёсткими стенками, диаметр которого меньше длины волны, то
в нём должна была бы формироваться плоская волна (гидроволна), такая же, как в
неограниченном пространстве (рис. 1, б). Реально же при увеличении отношения
длины волны l к толщине зазора (l/Dd>l) гидроволна вырождается. Как будет
показано ниже, её интенсивность существенно меньше, чем это обычно
представляется. Временной интервал, в котором ожидается появление гидроволны,
заполнен преимущественно колебаниями интенсивной волны Стоунли.
В обсаженной
скважине интервалы свободной незацементированной колонны представляют собой
упругий волновод со свободными границами, в котором распростаняются нормальные
волны - продольные (волны Лэмба в классическом их понимании) и поперечная. При
малой толщине колонны, когда wh/vs<<l, что всегда выполняется
в скважине на частотах АК, в колонне возможно распространение только нормальных
волн нулевого порядка: двух волн Лэмба и одной поперечной волны. Симметричная
продольная волна Лэмба соответствует Р волне в неограниченном пространстве. В
ней преобладает продольная компонента смещения, и только потому, что
поверхности колонны свободные, появляется небольшое поперечное смещение,
которое в vs/wh раз меньше продольного. Фазовая скорость этой волны
несколько меньше скорости Р волны в неограниченном пространстве и равна
примерно 5350-5400 м/с (рис. 1, рис. 2). Собственно это волна, которая в
акустической цементометрии носит наименование "волны по колонне".
РИС. 1. СХЕМАТИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПАКЕТОВ ВОЛН,
РАСПРОСТРАНЯЮЩИХСЯ В СКВАЖИНЕ:
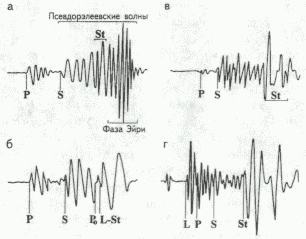
а - при невозможности
идентификации волн, вступающих после первого периода S волны; б - при допущении
распространения волн Лэмба в столбе скважинной жидкости; в - в открытой
скважине; г - в обсаженной скважине при условии частичного цементирования/
РИС. 2. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ИНТЕРВАЛЬНЫХ ВРЕМЕН (DT) И
ВРЕМЕННЫХ ИНТЕРВАЛОВ СУЩЕСТВОВАНИЯ ВОЛН ЛЭМБА, ПРОДОЛЬНОЙ, ПОПЕРЕЧНОЙ, СТОУНЛИ;
ИДЕНТИФИКАЦИЯ ТИПОВ ВОЛН, ЗАРЕГИСТРИРОВАННЫХ В ОБСАЖЕННОЙ СКВАЖИНЕ:
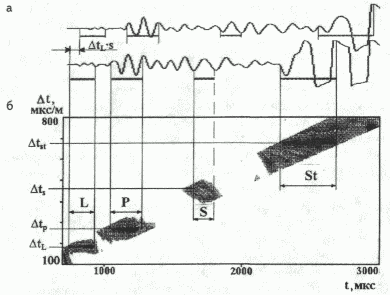
а - анализируемый пакет
упругих волн; б - временное поле локальных максимумов коэффициентов корреляции
33. Основные
расчетные соотношения при последовательном и параллельном соединении труб
Простые
трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным
или параллельным.
Последовательное
соединение. Возьмем несколько труб различной длины, разного диаметра и
содержащих разные местные сопротивления, и соединим их последовательно (рис.1,
а).
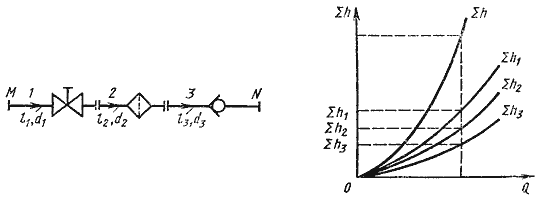
Рис. 1.
Последовательное соединение трубопроводов
При подаче
жидкости по такому составному трубопроводу от точки М к точке N
расход жидкости Q во всех последовательно соединенных трубах 1, 2
и 3 будет одинаков, а полная потеря напора между точками М и N
равна сумме потерь напора во всех последовательно соединенных трубах. Таким
образом, для последовательного соединения имеем следующие основные уравнения:
Q1
= Q2 = Q3 = Q
ΣhM-N
= Σh1 + Σh2
+ Σh3
Эти уравнения
определяют правила построения характеристик последовательного соединения труб
(рис. 1, б). Если известны характеристики каждого трубопровода, то по ним можно
построить характеристику всего последовательного соединения M-N. Для
этого нужно сложить ординаты всех трех кривых.
Параллельное
соединение. Такое соединение показано на рис. 2, а. Трубопроводы 1, 2
и 3 расположены горизонтально.
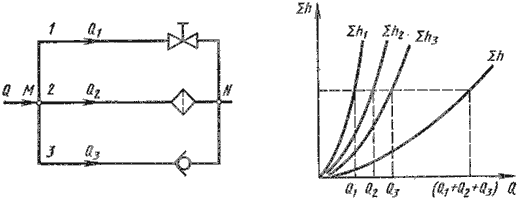
Рис. 2.
Параллельное соединение трубопроводов
Обозначим
полные напоры в точках М и N соответственно HM
и HN , расход в основной магистрали (т.е. до разветвления и
после слияния) - через Q, а в параллельных трубопроводах через Q1,
Q2 и Q3; суммарные потери в этих
трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что
расход жидкости в основной магистрали
Q = Q1
= Q2 = Q3
Выразим
потери напора в каждом из трубопроводов через полные напоры в точках М и
N :
Σh1
= HM - HN; Σh2
= HM - HN; Σh3
= HM - HN
Отсюда делаем
вывод, что
Σh1
= Σh2 = Σh3
т.е. потери
напора в параллельных трубопроводах равны между собой. Их можно выразить в
общем виде через соответствующие расходы следующим образом
Σh1
= K1Q1m;
Σh2 = K2Q2m;
Σh3 = K3Q3m
где K
и m - определяются в зависимости от режима течения.
Из двух
последних уравнений вытекает следующее правило: для построения характеристики
параллельного соединения нескольких трубопроводов следует сложить абсциссы
(расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h).
Пример такого построения дан на рис. 1, б.
Задача 1
Определить величину и
направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня
находится воздух, слева от поршня и в резервуаре, куда опущен открытый конец
трубы – масло турбинное. Показание пружинного манометра – 100000 Па. Дано: Н=5м,
D= 160 мм, d=80 мм; r = 940
кг/м3.
Решение:

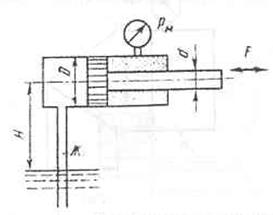
Для удержания поршня на
месте необходимо приложить силу, направленную от поршня, как показано на
рисунке жирной стрелкой.
По величине эта сила
должна уравновесить силу давления разряженного воздуха в полости цилиндра, а
также поднятую на высоту Н = 5 м. и ообладающей плотностью r = 940
кг/м3.
Учитывая условие
уравновешивания силы давления со стороны воздуха Р1 (с учетом того,
что манометр показывает абсолютное давление) и со стороны жидкости Р2,
по модулю эта сила равна
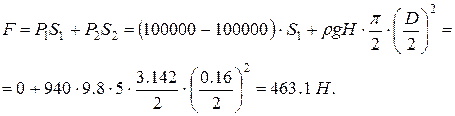
В этой сумме первое
слагаемое нулевое, т.к. показание пружинного манометра 100000 Па, а так как это
давление абсолютное, то для его учета нужно отнять величину атмосферного
давления, т.е. 100000 Па; при этом не имеет смысла рассчитывать величину S1, т.к. все равно будет умножение на 0.
Ответ: 463,1 Н;
направлена вправо от поршня.
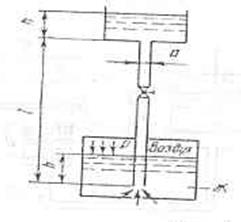
Задача 8
Жидкость (вода) попадает
в открытый верхний бак по вертикальной
трубе длиной 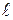 = 10 м, и диаметром d = 80 мм за счет давления воздуха в
нижнем замкнутом резервуаре. Определить давление р воздуха, при котором расход
будет равен Q = 8 л/с. Принять при этом
= 10 м, и диаметром d = 80 мм за счет давления воздуха в
нижнем замкнутом резервуаре. Определить давление р воздуха, при котором расход
будет равен Q = 8 л/с. Принять при этом 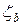 = 8, Sкл = 0,5,
= 8, Sкл = 0,5, 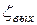 = 1, Rе = 0,2 мм.
= 1, Rе = 0,2 мм.
Решение:
Эквивалентная
шероховатость выражается через велчину потерь от трения 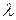 т и диаметр трубы следующим образом: Rе = (
т и диаметр трубы следующим образом: Rе = (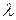 т / 0,11)4 d.
т / 0,11)4 d.
Выразим отсюда потреи от
трения 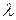 т с переводом миллиметров в метры:
т с переводом миллиметров в метры:
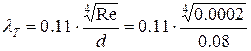 т = 0,0254.
т = 0,0254.
Уравнение Бернулли:
r·u2/2 + Р + r·g·h = соnst.
Уравнение Бернулли для этой
системы:
Р + r·g·(l – Shпот) = r·g·h + Ратм.
Перенося соответствующие
слагаемые в разные части уравнения. Получим, что перепад давлений вычисляется
по формуле
Р – Ратм = (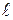 +
+ 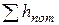 )
) 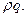
Суммарные потери напора
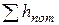 = (
= (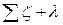 т *
т * 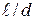 ) *
) * 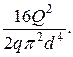
В результате получаем
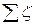 +
+ 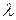 т *
т * 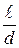 = 12,4
= 12,4
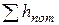 = 2,7
= 2,7
Р – Ратм = 24
кПа.
Поскольку атмосферное
давление равно 100 кПа, то Р = 124 кПа.
Ответ: Р = 1,24 атм.
Задача 17
Из бака А, в котором
поддерживается постоянный уровень, вода протекает по цилиндрическому насадку
диаметром d=30 мм в бак В, из которого сливается
в атмосферу по короткой трубе диаметром D=38 мм, снабженной краном. Определить
наибольшее значение коэффициента сопротивления крана 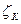 , при котором истечение из насадка будет осуществляться в
атмосферу. Потери на трение в трубе не учитывать.
, при котором истечение из насадка будет осуществляться в
атмосферу. Потери на трение в трубе не учитывать.
Дано: h = 50 см; Н = 140 см.
Решение:
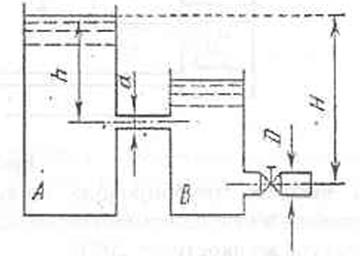
Максимальное
сопротивление крана будем находить из условия равенства расхода воды через
трубу диаметром d=30 мм и через трубу диаметром D=37 мм, причем сопротивление при
истечении воды через трубу d=30 мм не учитываем.
Расход воды через
короткую трубу без насадка:
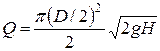 .
.
При наличии насадка
необходимо в формулу для рассчета расхода воды ввести поправочный множитель (коэффициент
сопротивления крана) и учесть разницу диаметров:
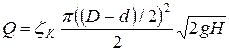 .
.
Расход воды в атмосыеру
будет осуществляться при соблюдении условия:
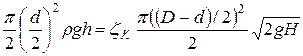 .
.
После элементарных
преобразований:
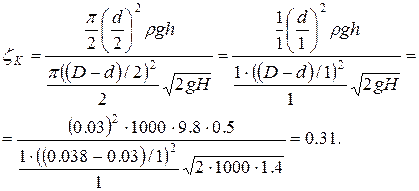 .
.
Ответ: 0,31.
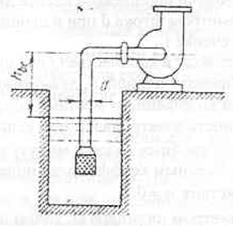
Задача 22
Центробежный насос
производительностью Q=22 л/с работает при частоте вращения
п=2890 об/мин. Определить
допустимую высоту всасывания, если диаметр всасывающей трубы d=125 мм, а ее длина l=3 м. Коэффициент кавитации в формуле
Руднева принять равным С=900.
Температура воды t=20°С. Коэффициент сопротивления колена 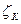 =0,2. Коэффициент сопротивления входа в трубу
=0,2. Коэффициент сопротивления входа в трубу 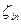 =1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.
=1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.
Решение:
Расход воды
рассчитывается по формуле:
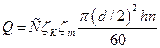 .
.
Выразим из этой формулы
искомую величину (высоту) и подставим исходные данные задачи, учитывая, что 22
л/с равен 0,022 м3/с:
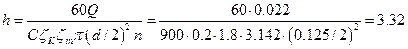 м.
м.
Ответ: 3,32 м.
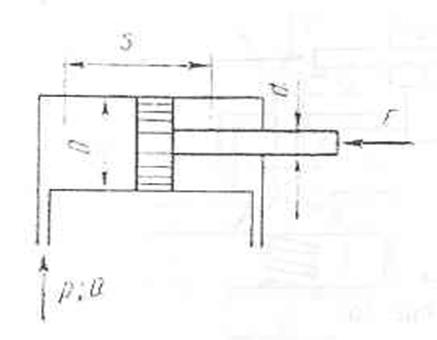
Задача 30
Поршневой насос простого
действия с диаметром цилиндра D=70 мм, ходом поршня S=240 мм, числом двойных ходов в
минуту п=70 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
систему гидропровода. При какой частоте вращения должен работать включенный
параллельно шестеренный насос с начальным диаметром шестерен d=56 мм, шириной шестерен b=5 мм, числом зубьев z=30 и объемным КПД hоб=0,86, чтобы количество подаваемой
жидкости удвоилось?
Решение:
Поршневой насос простого
действия с диаметром цилиндра D=70 мм, ходом поршня S=240 мм, числом двойных ходов в
минуту п=70 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
количестве
Поршневой насос
обеспечивает подачу жидкости
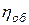 *
* 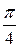 D2 S n, шестеренный насос -
D2 S n, шестеренный насос - 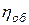 * 2
* 2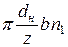
Значит, n1 = 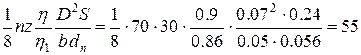 об/мин.
об/мин.
Ответ: n1 = 55 об/мин.
Задача 40
Пользуясь характеристикой
гидромуфты, определить расчетный и максимальный моменты, передаваемые ею, а
также передаточное отношение, коэффициент полезного действия и скольжение при
этих режимах, если активный диаметр гидромуфты D=430 см, частота вращения ведущего
вала n=1800 об/мин, рабочая жидкость – трансформаторное масло. Как
изменяется передаваемые крутящий момент
и мощность, если частоту вращения ведущего вала увеличить в полтора раза?
Характеристики
гидромуфты:
|

|
0
|
0,2
|
0,4
|
0,6
|
0,8
|
0,9
|
1
|
|
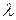 ,
мин2/м. ,
мин2/м.
|
0,000006
|
0,00000565
|
0,00000511
|
0,00000431
|
0,00000321
|
0,00000241
|
0
|
Решение:
В гидромуфте
(гидропередача без внешней опоры) момент на турбине всегда равен моменту на
насосе, но передача энергии в ней происходит с определенными потерями,
характеризуемыми в рабочем режиме значением К.П.Д. Поскольку
моменты колес раны, то К.П.Д. численно равен отношению частоты вращения
турбины n2 к частоте вращения насоса n1, т.е.
передаточному отношению i ( i= n2/n1).
Момент гидромуфты Мг подчиняется зависимости
М = λi·ρ·(n
/ 60)2·Da,
где:
λi -
коэффициент момента, являющийся параметром гидромуфты данного типа при заданном
значении i, ρ-плотность РЖ, Da- активный диаметр, равный
наибольшему диаметру рабочей полости гидромуфты.
Отсюда искомый активный диаметр:
Da = М / (λi·ρ·(n
/ 60)2) = 350 / (60∙10-7 ∙ 8600 ∙ (1100
/ 60)2) = 0,202 м.
Построим внешнюю
(моментальную) характеристику гидравлической муфты. В эту характеристику
входят:
1) момент муфты: М = 350 Н∙м;
2) коэффициент момента λi =
60∙10-7 мин2/м;
3) активный диаметр: Da
= 0,202 м;
4) частота вращения п =
1800 об/мин.
Для полноты приведем
графическую иллюстрацию зависимости коэффициента момента от передаточного
числа:
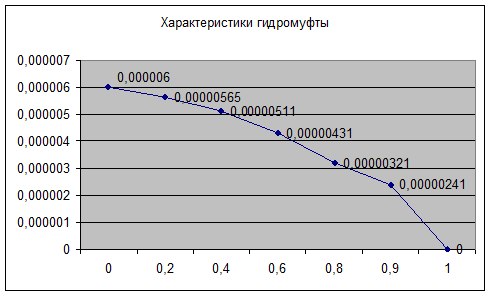
Ответ: момент гидромуфты 350
Н∙м.
Список
литературы
1.
Башта
Т.М., Руднев С.С. Гидравлика, гидромашины и гидропривод. – М.: Машиностроение,
1982.
2.
Дергачев
Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
3.
Задачник
по гидравлике, гидромашинам и гидроприводу / под ред. Б.Б. Некрасова. – М.:
Высшая школа, 1989.
4.
Осипов
П.Е. Гидравлика, гидромашины и гидропривод. – М.: Лесная промышленность, 1981.
5.
Юфин
А.П. Гидравлика, гидромашины и гидропривод. – М.: