Введение

В большинстве задач программирования используются алгоритмы. При этом циклические алгоритмы являются наиболее распространенным видом алгоритмов. Одним из важнейших этапов разработки алгоритма является его отладка. В настоящей работе рассматриваются циклические алгоритмы, в том числе особенности их отладки.

Понятие алгоритма

Термин алгоритм применяют весьма широко и не только в области вычислительной техники и программирования. Он происходит от имени средневекового математика Абу Джафара ибн Муссы аль-Хорезми. Редакция последней части имени ученого в европейских языках привела к образованию термина «алгорифм» или «алгоритм». Европейцы, начавшие осваивать современную десятичную систему счисления в XII в., знакомились с трудами арабских ученых, и труд упомянутого выше жителя Хорезма, посвященный правилам счета в десятичной системе счисления, был широко известен. Поэтому и наполнение термина «алгоритм» было следующим: операции над числами.

Современное содержание понятия алгоритма можно определить следующим образом.

Алгоритм – точное предписание, которое задает алгоритмический процесс, начинающийся с произвольного исходного данного (из некоторой совокупности возможных для данного алгоритма исходных данных) и направленный на получение полностью определенного этим исходным данным результата.[1]

Алгоритмический процесс – процесс последовательного преобразование конструктивных объектов (слов, чисел, пар слов, пар чисел, предложений и т.п.), происходящий дискретными «шагами». Каждый шаг состоит в смене одного конструктивного объекта другим.

Как правило, для заданного алгоритма можно выделить семь характеризующих его независимых параметров:

· совокупность возможных исходных данных;

· совокупность возможных промежуточных результатов;

· совокупность результатов;

· правило начала;

· правило непосредственной переработки;

· правило окончания;

· правило извлечения результата.

В теории алгоритмов изучаются алгоритмы, заданные в строгом, формализованном виде.

На практике в программировании очень часто используется задание алгоритмов в виде блок-схем.

Блок-схема – это ориентированный граф, вершины которого могут быть одного из трех типов.

Функциональная вершина используется для представления функции f: X→Y.

Предикатная вершина используется для представления функции (или предиката) p: X→(T,F), т.е. логического выражения, передающего управление по одной из двух возможных ветвей.

Объединяющая вершина представляет передачу управления от одной из двух входящих ветвей к одной выходящей ветви[2].

Определение и типовая схема циклического алгоритма

Циклические алгоритмы являются наиболее распространенным видом алгоритмов, в них предусматривается повторное выполнение определенного набора действий при выполнении некоторого условия.

Циклическим называют алгоритм, в котором получение результата обеспечивается многократным выполнением одних и тех же операций.

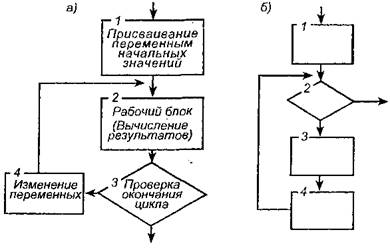
Структуру любого циклического алгоритма можно изобразить схемами, представленными на рисунке ниже (а,б).

Возможны еще два варианта подобных схем. Они содержат те же четыре блока, что и схемы на рисунке, но расположенные в ином порядке.

Назначение блоков циклического алгоритма

Вернемся к определению циклического алгоритма. Из него следует, что основой такого алгоритма являются операции, многократное выполнение которых дает искомый результат. Такие операции называют рабочими. Совокупность этих операций образует тело цикла.

Выполнение циклического алгоритма распадается на этапы – их называют циклами, на каждом из которых выполняются операции блоков 2, 3, 4, т.е. на каждом цикле вычисляются новые значения аргументов (в блоке 4) и соответствующие им новые значения результатов рабочих операций (в блоке 2), результатов промежуточных или окончательных.

Блоки 1 и 3 обычно задают диапазон изменения аргументов. Блок 1 присваивает всем аргументам начальные значения, обеспечивая тем самым выполнение рабочих операций на первом цикле.

В блоке 3 проверяется условие окончания (повторения) цикла, чаще всего предполагающее сравнение текущего значения некоторой переменной с ее предельным значением.

В общем случае условие окончания (повторения) цикла может быть явно не связано ни с аргументами, ни с их конечными значениями.

Вывод: любой циклический алгоритм определяется тремя наборами формул (содержащихся в блоках 1, 2, 4) и одним условием (отношением, логическим выражением)[3].

Виды циклических алгоритмов

Циклические алгоритмы бывают двух основных видов:

1) циклические алгоритмы по количеству повторений (циклы со счетчиком), когда к моменту выполнения цикла заранее известно, сколько раз его нужно выполнить;

2) циклические алгоритмы по условию, когда циклические действия продолжаются до тех пор, пока не будет выполнено какое-либо условие.

Циклические алгоритмы с условием, в свою очередь, делятся на циклические алгоритмы с предусловием (каждый раз проверяется истинность или ложность условия перед выполнением тела цикла) и циклические алгоритмы с постусловием (истинность или ложность условия проверяется после выполнения тела цикла).

Циклические алгоритмы с предусловием используют в случае, когда циклическими действиями управляет логическое условие и к моменту выполнения цикла не ясно, сколько раз нужно повторить циклические действия. Последовательность действий данного оператора цикла заключается в следующем: сначала вычисляется логическое выражение. Если оно истинно, то выполняется тело цикла до тех пор, пока условие не примет значение ложь.

Циклические алгоритмы с предусловием, как правило, используют в задачах, где требуется организовать итерационный алгоритм.

Циклические алгоритмы с постусловием используют в случае, когда циклическими действиями управляет логическое условие и к моменту выполнения цикла не ясно, сколько раз нужно выполнить циклические действия. Последовательность действий данного оператора цикла заключается в следующем: выполняется тело цикла до тех пор, пока условие не примет значение истина.

Циклические алгоритмы по количеству повторений используют в случае, когда к моменту выполнения циклических действий известно, сколько раз требуется выполнить цикл. Значение параметра цикла последовательно наращивается до заданной верхней или последовательно уменьшается до известной нижней границы[4].

Отладка алгоритмов

Алгоритм можно использовать только в том случае, если он верен. Однако на практике в любом достаточно сложном алгоритме (если не принять специальных мер) обязательно содержатся ошибки. Поэтому любой вновь составленный алгоритм нужно «отладить».

Отладкой алгоритма называется процесс выявления и исправления ошибок в нем. Суть отладки алгоритма в том, что выбирается некоторый набор исходных данных, называемый тестовым набором (тестом), и задача с этим набором решается дважды (либо выбирают такой набор данных, при котором результаты решения заранее известны): один раз – исполнением алгоритма, второй раз – каким-либо иным способом, исходя из условия задачи, так сказать, «вручную». При совпадении результатов алгоритм считается верным. В качестве тестового набора можно выбрать любые данные, которые позволяют:

1)    обеспечить проверку выполнения всех операций алгоритма;

2)    свести количество вычислений к минимуму[5].

В случае отладки циклических алгоритмов тест может содержать один набор данных и выбирается таким образом, чтобы обеспечить проверку выполнения всех блоков и ветвей алгоритма при небольшом числе повторения цикла (три, четыре)[6].

Заключение

В настоящей работе было рассмотрено понятие алгоритма, в том числе циклического алгоритма, описана типовая структура циклического алгоритма и его виды.

Кроме того, отмечена значимость отладки алгоритмов, описан процесс отладки алгоритмов и особенности отладки циклических алгоритмов.

Задание 1.18

Составить алгоритм линейной структуры:

Даны длины сторон прямоугольного параллепипеда. Найти его объем и площадь боковой поверхности.

Решение

Где S – площадь боковой поверхности, V – объем, a, b, c – длины сторон параллепипеда.

Задание 2.8

Составить алгоритм разветвленной структуры:

Дана масса двух тел из разных материалов. Материал, какого из тел имеет большую плотность?

Решение

Где m1, m2 – массы тел, V1, V2 – объемы тел, ρ1, ρ2 – плотности тел.

Задание 3.8

Составить алгоритм циклической структуры:

Найти сумму квадратов всех целых чисел от a до b (значения a и b вводятся с клавиатуры, b≥a).

Решение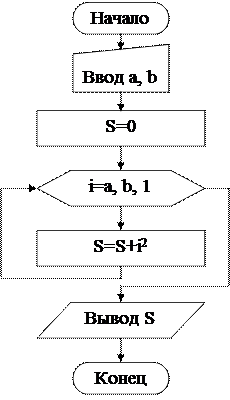

Где a, b – границы интервала, S – сумма квадратов всех целых чисел, i – временная переменная.

Задание 4.8

Составить алгоритм вложенной циклической структуры (массивы):

У фирмы имеется 3 магазина. Известен доход каждого магазина за каждый из десяти дней.

Организовать ввод информации по таблице:

Магазин

Дата

1

2

3

4

5

6

7

8

9

10

1

2

3

и определить:

·        какой из магазинов получил максимальный общий доход за 10 дней;

·        какого числа фирма получила максимальный общий доход;

·        какой магазин, и какого числа получил максимальный доход за день;

·        для каждого магазина определить, какого числа в этом магазине был получен максимальный доход;

·        для каждого дня определить средний доход по всем магазинам.

Решение

Где M[3][10] – массив, содержащий данные о том, какой доход каждый из магазинов получил в каждый из десяти дней, Dm[3] – массив, содержащий данные о том, какой максимальный общий доход получил каждый из магазинов за десять дней, Df – наибольший доход фирмы за день, d – день, в который фирма получила максимальный доход, Sd – суммарный доход фирмы за день, Mm[3][2] – массив, содержащий данные о том, какой максимальный доход за день получил каждый из магазинов и в какой день, Sr[10] – среднее значение дохода фирмы за каждый из десяти дней, i, j – временные переменные.

Список литературы

1)    Коуров Л.В. Информационные технологи. – Минск: Амалфея, 2000

2)    Компьютерные технологии обработки информации/ Под ред. С.В. Назарова. _ М.: Финансы и статистика, 2001.

3)    Введение в информационный бизнес; Учеб. пособ. / Под ред. В.П. Тихомирова, А.В. Хорошилова. – М.: Финансы и статистика, 2002

4)    Муртазин Э.В. Интернет: Учебник. – М.: ДМК, 2004

5)    Основы современных компьютерных технологий: Учеб. пособ./ Под ред. А.Д. Хомоненко. – Спб.: Корона принт, 2002

6)    Дюк В. Обработка данных на ПК в примерах. – Спб.: Питер, 2002

7)    Острейковский В.А. «Информатика: Учеб. для вузов». – 2-е изд., стер. – М.: Высш. шк., 2004. – 511 с.: ил.

8)    Ляхович В.Ф., Крамаров С.О. «Основы информатики». Изд. 2-е, доп. и перер. – Ростов н/Д: изд-во «Феникс», 2003. – 704 с.

9)    «Задачник по программированию для математиков», учебное пособие под ред. Старченко А.В. – Томск: изд-во ТГУ, 2001. В эл. виде.

[1] Компьютерные технологии обработки информации/ Под ред. С.В. Назарова. _ М.: Финансы и статистика, 2001. – с. 158.

[2] Острейковский В.А. «Информатика: Учеб. для вузов». Стр. 187-190.

[3] Компьютерные технологии обработки информации/ Под ред. С.В. Назарова. _ М.: Финансы и статистика, 2001. – с. 421-423.

[4] «Задачник по программированию для математиков», учебное пособие под ред. Старченко А.В.

[5] Ляхович В.Ф., Крамаров С.О. «Основы информатики». Стр. 385-387.

[6] Ляхович В.Ф., Крамаров С.О. «Основы информатики». Стр. 444.