ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-КОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ:
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И
ПРИКЛАДНЫЕ МОДЕЛИ
ВАРИАНТ 7
Оглавление
Задание
1. 2
Задача
2. 6
Задача
3. 10
Задание 1
Завод-производитель высокоточных элементов для автомобилей
выпускает два различных типа деталей – Х и У. Завод располагает фондом рабочего
времени в 4000 чел.-ч. В неделю. Для производства
одной детали типа Х требуется 1 чел.-час, а для
производства одной детали типа У – 2 чел.-час.
Производственные мощности завода позволяют выпускать максимум 2250 деталей типа
Х и 1750 деталей типа У в неделю. Каждая деталь типа Х требует 2 кг металлических стержней и 5 кг листового металла.
Уровень запасов каждого вида металла составляет 10000 кг в неделю. Кроме
того, еженедельно завод поставляет 600 деталей типа Х своему постоянному
заказчику. Существует также профессиональное соглашение, в соответствии с
которым общее число производимых в течение одной недели деталей должно
составлять не менее 1500 штук.
Сколько деталей следует производить, чтобы максимизировать
общий доход за неделю, если доход от производства одной детали типа Х
составляет 30 ден.ед., а от производства одной детали
типа У – 40 ден.ед.
Построить экономико-математическую модель задачи, дать
необходимые комментарии к ее элементам и получить решение графическим методом.
Что произойдет, если решить задачу на минимум и почему?
Решение
Пусть:
х1 – количество производимых деталей Х
х2 – количество производимых деталей У
|
Целевая функция:
|
|
|
max z = 30
∙ x + 40 ∙ у
|
Необходимо максимизировать общий
доход завода
|
|
Ограничения:
|
|
|
х +
2∙ у ≤ 4000
|
Фонд рабочего времени в неделю
ограничен 4000 часами
|
|
х
≤ 2250
у ≤ 1750
|
Ограничение по производственной
мощности завода (может производить максимум 2250 ед. деталей Х и 1750 деталей
У в неделю)
|
|
2 ∙ х
+ 5 ∙ у ≤ 10 000
|
Уровень запасов стержней ограничен
10 000 ед.
|
|
5 ∙ х
+ с ∙ у ≤ 10 000
|
Уровень запасов листов ограничен10
000 ед.
|
|
х
≥ 600
|
Ограничение по количеству деталей
Х (необходимо минимум 600 ед. в неделю)
|
|
x + y ≥ 1500
|
Ограничение по количеству деталей,
производимых на заводе (необходимо минимум 1500 ед. в неделю)
|
|
x; у ≥ 0
|
Количество потребляемых кормов не
может быть отрицательным
|
Решим задачу графически.
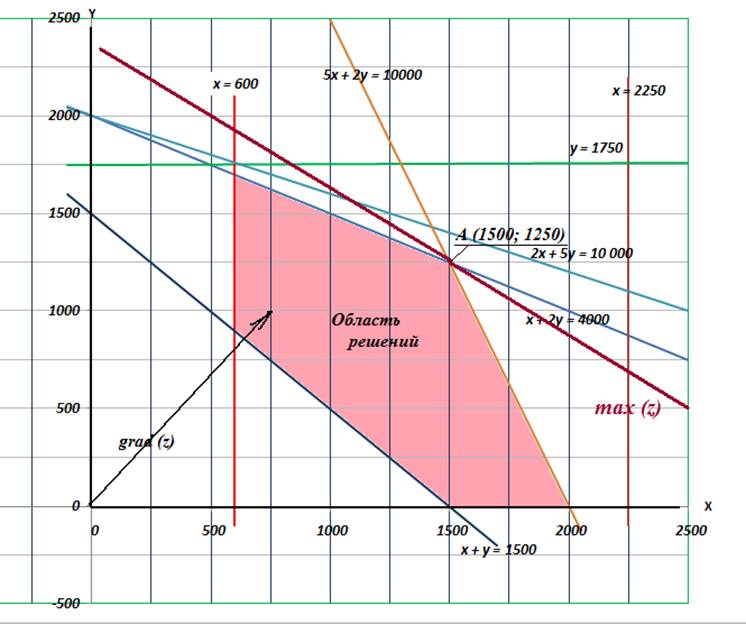
Рисунок 1.
Графическое решение задачи
Область решения задачи ограничена кривыми ограничений
целевой функции и представлена на графике штриховкой.
Направление роста целевой функции показывает градиент этой
функции.
Исходя из графика, максимальное значение функции z будет при пересечении
графиков х + 2у = 4000 и 5х + 2у = 10000. Решив
систему уравнений получим х = 1500 у = 1250
Таким образом, максимально возможная прибыль составляет
z = 30
∙ 1500 + 40 ∙ 1250 = 95000 ден.ед.
Минимальная выручка будет в точке х
= 1500 у = 0 и составит
zmin = 30 ∙ 1500 = 45000 ден.ед.
Задача 2
Предприятие выпускает четыре вида
продукции и использует три вида оборудования: токарное, фрезерное,
шлифовальное. Общий фонд рабочего времени оборудования каждого вида, нормы
расхода и цены реализации единицы каждого вида продукции приведены в таблице.
|
Тип оборудования
|
Нормы расхода ресурса на одно изделия
|
Фонд рабочего времени, ч.
|
|
А
|
Б
|
В
|
Г
|
|
Токарное
|
2
|
1
|
1
|
3
|
300
|
|
Фрезерное
|
1
|
|
2
|
1
|
70
|
|
Шлифовальное
|
1
|
2
|
1
|
0
|
340
|
|
Цена изделия
|
8
|
3
|
2
|
1
|
|
Требуется
1. Сформулировать
прямую оптимизационную задачу на максимум выручки от реализации готовой
продукции, получить оптимальный план выпуска продукции.
2. Сформулировать
двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3. Пояснить
нулевые значения переменных в оптимальном плане.
4. На
основе свойств двойственных оценок и теорем двойственности:
·
проанализировать использование ресурсов в
оптимальном плане исходной задачи;
·
определить, как изменятся выручка и план выпуска
продукции, если фонд рабочего времени шлифовального оборудования увеличить на
24 часа;
·
оценить целесообразность включения в план
изделия Д ценой 11 единиц, если нормы затрат оборудования 8, 2 и 2 единицы
соответственно.
Решение
Пусть x1
– количество производимой продукции А;
x2
– количество производимой продукции Б;
x3
– количество производимой продукции В;
x4
– количество производимой продукции Г.
Max f(x) = 8 ∙ x1 + 3 ∙ x2 + 2 ∙ x3 + 1 ∙ x4
2 ∙ x1
+ x2 + x3 + 3 ∙ x4 ≤ 300
x1
+ 2 ∙ x3
+ x4 ≤ 70
x1
+ 2 ∙ x2
+ x3 ≤ 340
xi
≥0
Решим задачу, используя пакет анализа «Поиск решения»

Таким образом, функция достигает максимального значения при
x1
=70
x2
= 135
x3
= 0
x4
= 0
max f(x) = 965
Двойственная задача имеет вид:
Min f(y) = 30 ∙ y1 + 70 ∙ y2 + 340 ∙ y3
2 ∙ y1
+ y2 + y3 ≥ 8
y1
+ 2 ∙ y3
≥ 3
y1
+ 2 ∙ y2
+ y3 ≥
2
3 ∙ y1
+ y2 ≥
1
yi ≥0 , i = {1, .. 3}
Найдем значения двойственных переменных, используя теоремы
двойственности.
Проверим, как удовлетворяется система функциональных
ограничений оптимальным планом:
|
у1 :
|
2 ∙ 70 + 135
+ 0 + 3 ∙ 0 = 275 ≤ 300
|
|
у2 :
|
70 + 2 ∙ 0 + 0
= 70
|
|
у3 :
|
70 + 2 ∙ 135 + 0 = 340
|
Так как первое ограничение выполняется как строгое
неравенство, то
у1 = 0.
Учитывая, что x1 ≥ 0 ; x2 ≥ 0, то значения остальных двойственных
переменных найдем из 1 и 2-го уравнений системы неравенств. То есть
2 ∙ y1
+ y2 + y3 = 8 (1)
y1
+ 2 ∙ y3
= 3 (2)
Решая систему из уравнений (1) и (2) получим:
у1 = 0;
у3 = 1,5;
у2 = 8 – 0 – 1,5 = 6,5.
Рассчитаем значение целевой функции двойственной задачи
Min f(y) = 30 ∙ 0 + 70
∙ 6,5 + 340 ∙ 1,5
Если стоимость ресурсов, затраченных на производство одного
изделия, больше его цены, то это изделие не войдет в оптимальный план из-за
своей убыточности. В нашей задаче это изделие В и Г. Подтвердим этот факт,
подставим в ограничения двойственной задачи оптимальные значения вектора Y.
2 ∙ 0 + 6,5 + 1,5 = 8
0 + 2 ∙ 1,5 = 3
0 + 2 ∙ 6,5 + 1,5 = 14,5 ≥ 2
3 ∙ 0 + 6,5= 6,5 ≥ 1
На основе двойственных оценок и теорем двойственности:
а)
Поясним использование ресурсов в оптимальном
плане исходной задачи.
В оптимальном плане не полностью используется сырье 1, т.к.
у1 = 0
Сырье 2 и 3 – дефицитное, т.к. их двойственные оценки
отличны от нуля.
б)
При увеличении фонда рабочего времени
шлифовального оборудования на 24 часа будет возможность получить дополнительную
выручку в размере 24 ∙ у3
= 24 ∙ 1,5 = 36 ден. ед.
в) оценим целесообразность включения в план изделия Д ценой
11 единиц, если нормы затрат оборудования 8, 2, 2 единицы.
8 ∙ y1
+ 2 ∙ y2
+ 2 ∙ y3
– ц < 0 – неравенство целесообразности включения в план нового изделия
8 ∙ 0 + 2 ∙ 6,5 + 2 ∙ 1,5 – 11 = 5 > 0 à нецелесообразно.
Задача 3
В течение девяти последовательных недель фиксировался спрос Y(t) (млн.руб.) на кредитные ресурсы
финансовой компании.
Линейная модель имеет вид: Yr(t) = a0 + a1
∙ t.
Параметры модели оценим с помощью МНК:
a1 = ∑ (xi
– xcr) ∙ (yi
– ycr) / ∑ (xi – xcr)2
a0 = ycr
– a1
∙ xcr
Составим разработочную таблицу:
|
|
х
|
у
|
(yi – ycr)
|
(xi – xcr)
|
(xi
– xcr)2
|
(xi – xcr) ∙ (yi – ycr)
|
|
|
1
|
20
|
-22,333
|
-4
|
16
|
89,333
|
|
|
2
|
27
|
-15,333
|
-3
|
9
|
46,000
|
|
|
3
|
30
|
-12,333
|
-2
|
4
|
24,667
|
|
|
4
|
41
|
-1,333
|
-1
|
1
|
1,333
|
|
|
5
|
45
|
2,667
|
0
|
0
|
0,000
|
|
|
6
|
51
|
8,667
|
1
|
1
|
8,667
|
|
|
7
|
51
|
8,667
|
2
|
4
|
17,333
|
|
|
8
|
55
|
12,667
|
3
|
9
|
38,000
|
|
|
9
|
61
|
18,667
|
4
|
16
|
74,667
|
|
Сумма
|
45
|
381
|
0,000
|
0
|
60
|
300,000
|
|
Среднее
|
5
|
42,333333
|
0,000
|
0
|
6,667
|
33,333
|
Отсюда
a1
= 300 / 60 = 5
a0
= 42,33 – 5 ∙ 5 = 17,33
Таким образом, линейная модель имеет вид:
Yr(t) = 17,33 + 5 ∙ t
Построим адаптивную модель Брауна 1
По первым пяти точкам ряда оцениваем значения а1
и а0 параметров модели с помощью МНК
|
|
х
|
у
|
уi - ycr
|
xi - xcr
|
(xi
- xcr)2
|
(xi-xcr)∙(yi-ycr)
|
|
|
1
|
20
|
-12,600
|
-2
|
4
|
25,200
|
|
|
2
|
27
|
-5,600
|
-1
|
1
|
5,600
|
|
|
3
|
30
|
-2,600
|
0
|
0
|
0,000
|
|
|
4
|
41
|
8,400
|
1
|
1
|
8,400
|
|
|
5
|
45
|
12,400
|
2
|
4
|
24,800
|
|
Сумма
|
15
|
163
|
0
|
0
|
10
|
64
|
|
Среднее
|
3
|
32,6
|
0
|
0
|
2
|
12,8
|
Получаем
a1
= 64 / 10 = 6,4
a0
= 32,6 – 6,4 ∙ 3 = 13,4
которые соответствуют моменту времени t=0
Прогноз на первый шаг у1расч = а0(0) +
а1(0) = 6,4 + 13,4 = 19,8
Величина отклонения: е = 20 – 19,8 = 0,2
Корректируем параметры (α = 0,4; β = 0,6)
a0(t)
= a0(t-1) + a1(t-1) + (1 – β2) ε (t) = 13,4 + 6,4 + (1 – 0,62)
∙ 0,2) = 19.928
a1(t) = a1(t-1) + (1 – β) 2 ε (t) = 6.4 + (1 – 0,6) 2 ∙ 0,2 = 6.432
Далее расчеты производятся аналогично.
|
t
|
y
|
a0
|
a1
|
yr
|
ε
|
|
0
|
|
13,400
|
6,400
|
|
|
|
1
|
20
|
19,928
|
6,432
|
19,800
|
0,200
|
|
2
|
27
|
26,770
|
6,534
|
26,360
|
0,640
|
|
3
|
30
|
31,189
|
6,006
|
33,304
|
-3,304
|
|
4
|
41
|
39,630
|
6,615
|
37,195
|
3,805
|
|
5
|
45
|
45,448
|
6,415
|
46,245
|
-1,245
|
|
6
|
51
|
51,311
|
6,277
|
51,863
|
-0,863
|
|
7
|
51
|
53,372
|
5,223
|
57,588
|
-6,588
|
|
8
|
55
|
56,294
|
4,648
|
58,595
|
-3,595
|
|
9
|
61
|
60,979
|
4,657
|
60,942
|
0,058
|
Построим адаптивную модель Брауна 2
Производятся аналогичные расчеты для α = 0,7; β =
0,3
|
t
|
y
|
a0
|
a1
|
yr
|
ε
|
|
0
|
|
13,400
|
6,400
|
|
|
|
1
|
20
|
19,982
|
6,498
|
19,800
|
0,200
|
|
2
|
27
|
26,953
|
6,753
|
26,480
|
0,520
|
|
3
|
30
|
30,334
|
4,937
|
33,706
|
-3,706
|
|
4
|
41
|
40,484
|
7,744
|
35,270
|
5,730
|
|
5
|
45
|
45,291
|
6,162
|
48,229
|
-3,229
|
|
6
|
51
|
51,041
|
5,940
|
51,453
|
-0,453
|
|
7
|
51
|
51,538
|
3,010
|
56,981
|
-5,981
|
|
8
|
55
|
54,959
|
3,231
|
54,548
|
0,452
|
|
9
|
61
|
60,747
|
4,608
|
58,190
|
2,810
|
Графики построенных моделей представлены на рисунке:
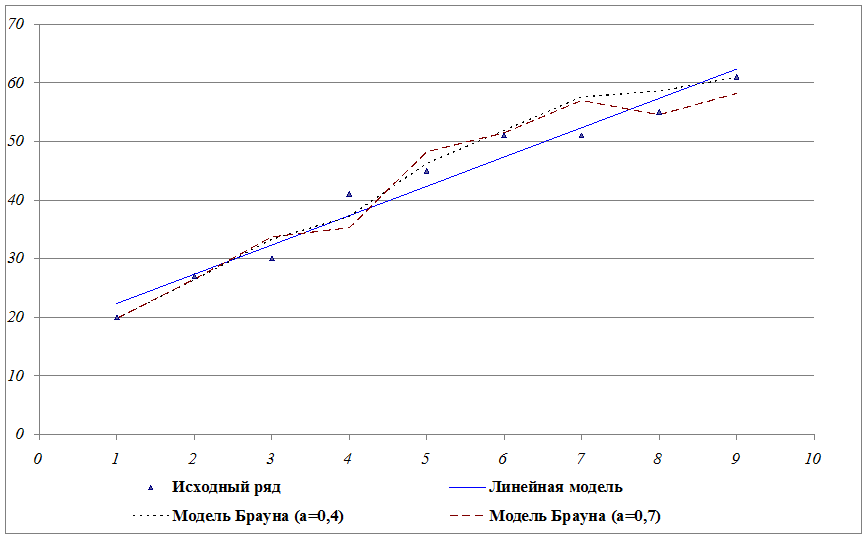
Рисунок 2
Временной ряд и построенные модели
Проведем качества каждой из моделей.
Линейная модель
|
х
|
у
|
yr
|
ε
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
Точки поворота
|
|
1
|
20
|
22,333
|
-2,333
|
5,444
|
-22,333
|
498,778
|
11,667
|
|
|
2
|
27
|
27,333
|
-0,333
|
0,111
|
-15,333
|
235,111
|
1,235
|
+
|
|
3
|
30
|
32,333
|
-2,333
|
5,444
|
-12,333
|
152,111
|
7,778
|
+
|
|
4
|
41
|
37,333
|
3,667
|
13,444
|
-1,333
|
1,778
|
8,943
|
+
|
|
5
|
45
|
42,333
|
2,667
|
7,111
|
2,667
|
7,111
|
5,926
|
+
|
|
6
|
51
|
47,333
|
3,667
|
13,444
|
8,667
|
75,111
|
7,190
|
+
|
|
7
|
51
|
52,333
|
-1,333
|
1,778
|
8,667
|
75,111
|
2,614
|
|
|
8
|
55
|
57,333
|
-2,333
|
5,444
|
12,667
|
160,444
|
4,242
|
+
|
|
9
|
61
|
62,333
|
-1,333
|
1,778
|
18,667
|
348,444
|
2,186
|
|
|
Итого
|
381
|
|
|
54,000
|
|
1554,000
|
51,780
|
|
|
Среднее
|
42,333
|
|
|
|
|
|
|
2,565
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р >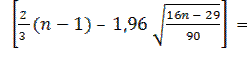 3,118
3,118
Учитывая, что неравенство выполняется, то есть 6 > 3,1 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:

Значение коэффициента F–критерия Фишера:
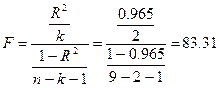
Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб,
уравнение регрессии следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.
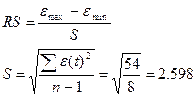
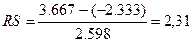
Учитывая, что полученное значение RS критерия попадает в интервал от 2,7
до 3,7, то уровни ряда остатков подчиняются нормальному закону распределения.
Средняя относительная ошибка аппроксимации:
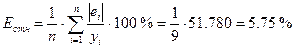
Еотн
= 5,75 < 7, что свидетельствует о хорошем качестве модели.
Модель Брауна 1:
|
х
|
у
|
yr
|
ε
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
Точки поворота
|
|
1
|
43
|
19,928
|
0,072
|
0,005
|
-22,333
|
498,778
|
0,360
|
|
|
2
|
47
|
26,770
|
0,230
|
0,053
|
-15,333
|
235,111
|
0,853
|
+
|
|
3
|
50
|
31,189
|
-1,189
|
1,415
|
-12,333
|
152,111
|
3,965
|
+
|
|
4
|
48
|
39,630
|
1,370
|
1,876
|
-1,333
|
1,778
|
3,341
|
+
|
|
5
|
54
|
45,448
|
-0,448
|
0,201
|
2,667
|
7,111
|
0,996
|
+
|
|
6
|
57
|
51,311
|
-0,311
|
0,097
|
8,667
|
75,111
|
0,610
|
+
|
|
7
|
61
|
53,372
|
-2,372
|
5,625
|
8,667
|
75,111
|
4,650
|
+
|
|
8
|
59
|
56,294
|
-1,294
|
1,675
|
12,667
|
160,444
|
2,353
|
|
|
9
|
65
|
60,979
|
0,021
|
0,000
|
18,667
|
348,444
|
0,034
|
|
|
Итого
|
381
|
|
|
10,947
|
|
1554,00
|
17,162
|
6
|
|
Среднее
|
42,333
|
|
|
|
|
|
|
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р>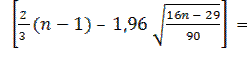 3,118
3,118
Учитывая, что неравенство выполняется, то есть 6 > 3 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:
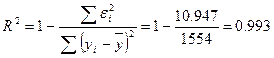
Значение коэффициента F–критерия Фишера:

Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб,
уравнение регрессии следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.


Учитывая, что полученное значение RS критерия не попадает в интервал от
2,7 до 3,7, то уровни ряда остатков не подчиняются нормальному закону
распределения.
Средняя относительная ошибка аппроксимации:
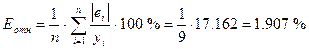
Еотн
= 1,907 < 7, что свидетельствует о хорошем качестве модели.
Модель Брауна 2:
|
х
|
у
|
yr
|
ε
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
Точки поворота
|
|
1
|
43
|
19,800
|
0,200
|
0,040
|
-22,333
|
498,778
|
1,000
|
|
|
2
|
47
|
26,480
|
0,520
|
0,270
|
-15,333
|
235,111
|
1,926
|
+
|
|
3
|
50
|
33,706
|
-3,706
|
13,734
|
-12,333
|
152,111
|
12,353
|
+
|
|
4
|
48
|
35,270
|
5,730
|
32,828
|
-1,333
|
1,778
|
13,975
|
+
|
|
5
|
54
|
48,229
|
-3,229
|
10,425
|
2,667
|
7,111
|
7,175
|
+
|
|
6
|
57
|
51,453
|
-0,453
|
0,205
|
8,667
|
75,111
|
0,888
|
+
|
|
7
|
61
|
56,981
|
-5,981
|
35,774
|
8,667
|
75,111
|
11,728
|
+
|
|
8
|
59
|
54,548
|
0,452
|
0,204
|
12,667
|
160,444
|
0,822
|
|
|
9
|
65
|
58,190
|
2,810
|
7,894
|
18,667
|
348,444
|
4,606
|
|
|
Итого
|
381
|
|
|
101,375
|
|
1554,000
|
54,472
|
6
|
|
Среднее
|
42,333
|
|
|
|
|
|
1,000
|
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р>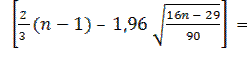 3,118
3,118
Учитывая, что неравенство выполняется, то есть 6 > 3 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:
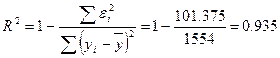
Значение коэффициента F–критерия Фишера:

Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб,
уравнение регрессии следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.
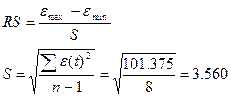
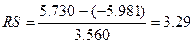
Учитывая, что полученное значение RS критерия не попадает в интервал от
2,7 до 3,7, то уровни ряда остатков не подчиняются нормальному закону
распределения.
Средняя относительная ошибка аппроксимации:
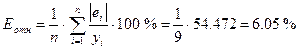
Еотн
= 6,05 < 7, что свидетельствует о хорошем качестве модели.
Таким образом можно сделать вывод
об адекватности Линейной модели и Модели Брауна 1.
Наиболее точна модель Брауна 1.
Построим прогноз спроса на следующие две недели на основе построенных
моделей.
Линейная модель:
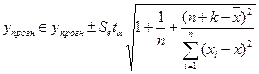
При вероятности 0,7 tα
= 1,119
1) При
t=10
t(10)= 17,33 + 5 ∙ 10 = 67,33
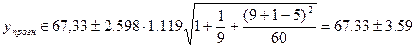
Или от 63,74 до 70,92.
2) При
t=11
t(10)= 17,33 + 5 ∙ 11 = 72,33
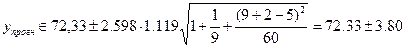
Или от 68,53 до 76,13.
Модель Брауна 1:
1) При
t=10
у (10)= а0(9) + а1(9)
∙ 1 = 60,979 + 4,657 ∙ 1 = 65,636
2) При
t=11
у (11)= а0(9) + а1(9)
∙ 2 = 60,979 + 4,657 ∙ 2 = 70,293
Модель Брауна 2:
3) При
t=10
у (10)= а0(9) + а1(9)
∙ 1 = 60,747 + 4,608 ∙ 1 = 65,355
4) При
t=11
у (10)= а0(9) + а1(9)
∙ 1 = 60,747 + 4,608 ∙ 2 = 69,963
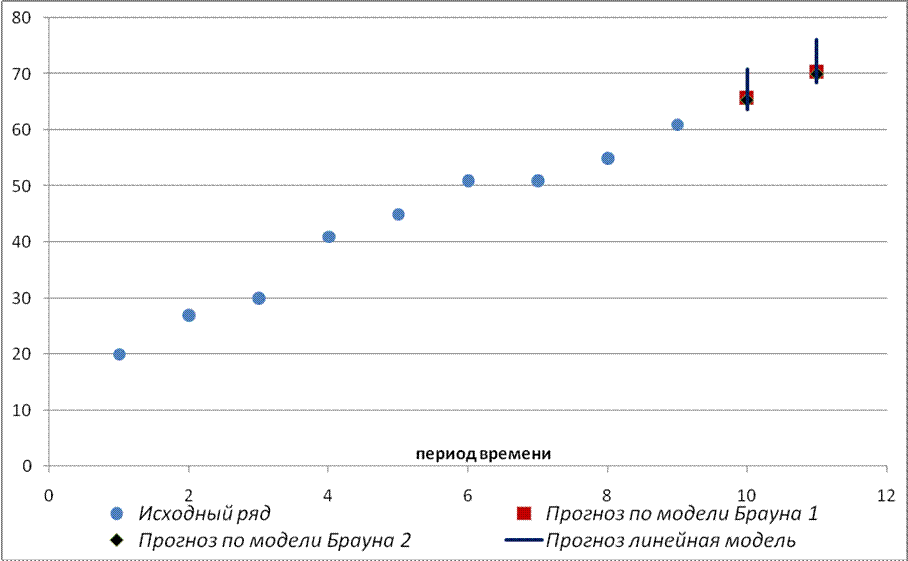
Рисунок 2
Прогноз временного ряда по построенным моделям