Содержание
Задание. 3
Тема 1: Логические основы системы Пролог-Д. 3
Логические основы работы.. 3
1.1.2. Описать на языке логики первого порядка свойства
отношения равенство 3
Тема 2: Построение базы знаний. 4
Факты и правила. 4
2.1.2. Опишите на языке Пролог-Д состав своей семьи. 4
Арифметика и другие второстепенные предикаты в Прологе-Д.. 9
2.2.2. Опишите на языке Пролог-Д вычисление площадей
геометрических фигур: трапеции, треугольника, параллелограмма. 9
2.2.3. Опишите вычисление пощади круга и длины
окружности. Какова точность вычисления этих величин? Можно ли вычислить радиус
круга по длине окружности?. 10
Рекурсия. 13
2.3.2.Написать на языке Пролог-Д базу знаний,
описывающую вычисление сумы чисел натурального ряда. 13
2.3.4. Описать вычисление наименьшего общего кратного. 14
Графические возможности системы Пролог-Д.. 16
2.4.2. Используя рекурсивное определение, напишите базу
знаний, описывающую многоэтажный дом. 16
Обработка списков. 20
2.5.2. Напишите базу знаний, описывающую обращение
списка (первый элемент становиться последним). 20
Заключение. 22
Список литературы.. 23
Задание
Тема 1: Логические основы системы Пролог-Д.
1. Логические основы работы.
1.1.2. Опишите на языке логики
первого порядка свойство отношения равенства
Тема 2: Построение базы знаний
1. Факты и правила
2.1.2. Опишите на языке Пролог-Д состав
своей семьи.
2. Арифметика и другие второстепенные
предикаты в Прологе-Д
2.2.2. Опишите на языке Пролог-Д
вычисление площадей геометрических фигур: трапеции, треугольника,
параллелограмма.
2.2.3. Опишите вычисление пощади
круга и длины окружности. Какова точность вычисления этих величин? Можно ли
вычислить радиус круга по длине окружности?
3. Рекурсия
2.3.2.Написать на языке Пролог-Д базу
знаний, описывающую вычисление сумы чисел натурального ряда.
2.3.4. Описать вычисление наименьшего
общего кратного.
4. Графические возможности системы
Пролог-Д
2.4.2. Используя рекурсивное
определение, напишите базу знаний, описывающую многоэтажный дом.
5. Обработка списков
2.5.2. Напишите базу знаний,
описывающую обращение списка (первый элемент становиться последним).
Тема 1: Логические основы системы
Пролог-Д.
Логические
основы работы
1.1.2. Описать на языке логики первого
порядка свойства отношения равенство
С помощью языка логики
первого порядка можно описать практически все задачи, решаемые на ЭВМ. В основе
системы Пролог-Д лежит этот язык.
Отношение равенство
запишем как РАВНО(X,Y). Это отношение принимает значение ИСТИНА, если X и Y равны между собой, и значение ЛОЖЬ
если X и Y не равны между собой. Отношение равенство обладает тремя свойствами:
рефлексивностью, симметричностью, транзитивностью:
§ переменная равна сама себе
(рефлексивность);
§ если X=Y, то Y=X (симметричность);
§ если X=Z
и Z=Y, то X=Z (транзитивность).
На языке логики первого порядка эти
свойства можно записать в следующем виде:
РАВНО (X,X)
РАВНО(X,Y)<-РАВНО(Y,X)
РАВНО(X,Y)<-РАВНО(X,Z)& РАВНО(Z,Y)
Тема 2: Построение
базы знаний
Факты
и правила
2.1.2. Опишите на
языке Пролог-Д состав своей семьи.
Пролог - язык программирования,
предназначенный в первую очередь для обработки символьной нечисловой
информации. Особенно хорошо он приспособлен для решения задач, в которых
фигурируют объекты и отношения между ними. К такому классу задач относиться и
задача описания родственных отношений. В нашей программе будут описаны
родственные связи, представленные на диаграмме (рис. 1).
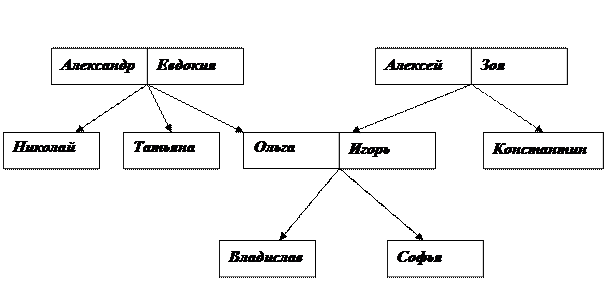
Рис. 1
Факты в программе были записаны с
помощью следующих фактов: мама (X, Y), папа (X, Y), мужчина(X), женщина(X). Факт, записанный с помощью предиката мама (X,Y), имеет место в программе, если X приходиться матерью Y. Факт, записанный с помощью
предиката папа (X,Y), имеет место в программе, если X является отцом Y. Факты мужчина (X) и женщина (X) имеют место, когда X является мужчиной или женщиной
соответственно.
Для построения правил в программе
использовались следующие утверждения:
§ X является родителем Y, если X –
является матерью или отцом Y;
§ X является сыном Y, если X – мужчина, и Y –
является родителем X;
§ X является дочерью Y, если X – женщина, и Y –
является родителем X;
§ X является бабушкой Y, если X – мама родителя Y;
§ X является дедушкой Y, если X – папа родителя Y;
§ X является сестрой Y, если X – женщина, X и
Y имеют одного отца и не являются одним и тем же лицом;
§ X является братом Y, если X – мужчина, X и
Y имеют одного отца и не являются одним и тем же лицом;
§ X является дядей Y, если X – мужчина, отец X и дедушка Y являются одним и тем же человеком
и X не является отцом Y;
§ X является тетей Y, если X – женщина, отец X и дедушка Y являются одним и тем же человеком
и X не является матерью Y;
§ X является племянником Y, если X – мужчина, дедушка X и отец Y являются одним и тем же человеком
и X не является сыном Y;
§ X является племянницей Y, если X – женщина, дедушка X и отец Y являются одним и тем же человеком
и X не является дочерью Y;
Для реализации вышеприведенных
утверждений были использованы стандартные предикаты РАВНО (Арг1,Арг2) и
НЕ(Арг1). Предикат РАВНО имеет два аргумента Арг1 и Арг2. Этот предикат
истинен, если успешна унификация Арг1 и Арг2. Аргументом встроенного предиката
НЕ является предикат, если этот предикат-аргумент ложен, то предикат НЕ
истинный, и наоборот.
Программа описывающая родственные
отношения с помощью системы Пролог-Д
имеет вид:
мама (Евдокия, Николай);
мама (Евдокия, Татьяна);
мама (Евдокия, Ольга);
мама (Зоя, Игорь);
мама (Зоя, Константин);
мама (Ольга, Владислав);
мама (Ольга, Софья);
папа (Александр, Николай);
папа (Александр, Татьяна);
папа (Александр, Ольга);
папа (Алексей, Игорь);
папа (Алексей, Константин);
папа (Игорь, Владислав);
папа (Игорь, Софья);
женщина(Евдокия);
женщина(Татьяна);
женщина(Ольга);
женщина(Зоя);
женщина(Софья);
мужчина(Александр);
мужчина(Николай);
мужчина(Алексей);
мужчина(Игорь);
мужчина(Константин);
мужчина(Владислав);
родитель(X,Y)<-мама(X,Y);
родитель(X,Y)<-папа(X,Y);
сын(X,Y)<-мужчина(X), родитель(Y,X);
дочь(X,Y)<-женщина(X),родитель(Y,X);
бабушка(X,Y)<-мама(X,Z),
родитель(Z,Y);
дедушка(X,Y)<-папа(X,Z),
родитель(Z,Y);
сестра(X,Y)<-женщина(X),папа(Z,X),папа(Z,Y),НЕ(РАВНО(X,Y));
брат(X,Y)<-мужчина(X),папа(Z,X),папа(Z,Y),НЕ(РАВНО(X,Y));
дядя(X,Y)<-мужчина(X),папа(Z,X),дедушка(Z,Y),НЕ(папа(X,Y));
тетя(X,Y)<-женщина(X),папа(Z,X),дедушка(Z,Y),НЕ(мама(X,Y));
племянник(X,Y)<-мужчина(X),дедушка(Z,X),папа(Z,Y),НЕ(сын(X,Y));
племянница(X,Y)<-женщина(X),дедушка(Z,X),папа(Z,Y),НЕ(дочь(X,Y));
Для проверки работы программы
попробуем выяснить следующие вопросы:
§ кто является родителями Владислава;
§ кто является сыном Алексея;
§ кто является дочерью Евдокии;
§ кто является бабушкой Софьи;
§ кто является дедушкой Софьи;
§ кто является сестрой Татьяны;
§ кто является дядей Софьи;
§ кто является тетей Владислава;
§ кто является племянником Константина;
§ кто является племянницей Николая?
Для этого зададим системе Пролог-Д
следующие вопросы:
?родитель(X, Владислав);
?сын(S, Алексей);
?дочь(D, Евдокия);
?бабушка(B, Софья);
?дедушка(Е, Софья);
?брат(W, Ольга);
?сестра(U, Татьяна);
?дядя(L, Софья);
?тетя(T, Владислав);
?племянник(P, Константин);
?племянница(N, Николай);
Ответ системы Пролог-Д:
X=Ольга
X=Игорь
S=Игорь
S=Константин
D=Татьяна
D=Ольга
B=Евдокия
B=Зоя
E=Александр
E=Алексей
W=Николай
U=Ольга
L=Николай
L=Константин
T=Татьяна
P=Владислав
N=Софья
Арифметика
и другие второстепенные предикаты в Прологе-Д
Пролог рассчитан главным образом на
обработку символьной информации, при которой потребность в арифметических
вычислениях относительно мала. Для осуществления основных арифметических
действий в системе Пролог-Д используются стандартные предикаты.
Стандартный предикат СЛОЖЕНИЕ (Арг1,
Арг2, Арг3), имеет три аргумента, связанных формулой Арг1+Арг2=Арг3.
Стандартный предикат УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеет три аргумента,
связанных формулой Арг1*Арг2=Арг3. С помощью этого предиката был введен еще
один вспомогательный предикат ДЕЛЕНИЕ(Арг1, Арг2, Арг3), его аргументы связаны
формулой Арг1/Арг2=Арг3:
ДЕЛЕНИЕ(x, y, z)<-УМНОЖЕНИЕ(z, y,
x);
2.2.2. Опишите на
языке Пролог-Д вычисление площадей геометрических фигур: трапеции,
треугольника, параллелограмма.
Вычисление площади
треугольника производиться по формуле 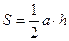 , где a – основание треугольника, а h – высота треугольника, проведенная к
этому основанию. Предикат, который
выполняется, если найдена площадь треугольника будет иметь имя треугольник и
три аргумента: a – основание треугольника, h – высота треугольник, S – вычисленная площадь. При
выполнении программы сначала вычисляется произведение
, где a – основание треугольника, а h – высота треугольника, проведенная к
этому основанию. Предикат, который
выполняется, если найдена площадь треугольника будет иметь имя треугольник и
три аргумента: a – основание треугольника, h – высота треугольник, S – вычисленная площадь. При
выполнении программы сначала вычисляется произведение 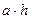 с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3). Далее полученное произведение делится
на 2 с помощью введенного предиката ДЕЛЕНИЕ (Арг1, Арг2, Арг3).
с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3). Далее полученное произведение делится
на 2 с помощью введенного предиката ДЕЛЕНИЕ (Арг1, Арг2, Арг3).
Вычисление площади параллелограмма осуществляется
по формуле 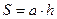 , где a – одна из сторон параллелограмма, а h – высота параллелограмма,
проведенная к стороне a. Предикат, который
выполняется, если найдена площадь параллелограмма будет иметь имя параллелограмм
и иметь три аргумента: a – сторона параллелограмма, h – его высота, S – вычисленная площадь. Площадь
параллелограмма вычисляется с помощью стандартного предиката УМНОЖЕНИЕ (Арг1,
Арг2, Арг3).
, где a – одна из сторон параллелограмма, а h – высота параллелограмма,
проведенная к стороне a. Предикат, который
выполняется, если найдена площадь параллелограмма будет иметь имя параллелограмм
и иметь три аргумента: a – сторона параллелограмма, h – его высота, S – вычисленная площадь. Площадь
параллелограмма вычисляется с помощью стандартного предиката УМНОЖЕНИЕ (Арг1,
Арг2, Арг3).
Площадь трапеции
вычисляется по формуле 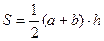 , где a, b – основания трапеции, а h – ее высота.
Предикат, который выполняется, если найдена площадь треугольника будет иметь
имя трапеция и иметь четыре аргумента: a, b – основания трапеции, h – высота трапеции, S – вычисленная площадь. Сначала
вычисляется сумма оснований с помощью стандартного предиката СЛОЖЕНИЕ (Арг1,
Арг2, Арг3), имеющего три аргумента, связанных формулой Арг1+Арг2=Арг3. Полученная
сумма умножается на высоту с помощью стандартного предиката УМНОЖЕНИЕ (Арг1,
Арг2, Арг3). Полученный результат делится на 2 с помощью предиката ДЕЛЕНИЕ
(Арг1, Арг2, Арг3).
, где a, b – основания трапеции, а h – ее высота.
Предикат, который выполняется, если найдена площадь треугольника будет иметь
имя трапеция и иметь четыре аргумента: a, b – основания трапеции, h – высота трапеции, S – вычисленная площадь. Сначала
вычисляется сумма оснований с помощью стандартного предиката СЛОЖЕНИЕ (Арг1,
Арг2, Арг3), имеющего три аргумента, связанных формулой Арг1+Арг2=Арг3. Полученная
сумма умножается на высоту с помощью стандартного предиката УМНОЖЕНИЕ (Арг1,
Арг2, Арг3). Полученный результат делится на 2 с помощью предиката ДЕЛЕНИЕ
(Арг1, Арг2, Арг3).
2.2.3. Опишите
вычисление пощади круга и длины окружности. Какова точность вычисления этих
величин? Можно ли вычислить радиус круга по длине окружности?
Число p было
введено в текст программы с помощь факта:
PI(3.14159);
Площадь круга вычисляется
по формуле 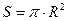 , где R – радиус круга. Предикат, который выполняется, если найдена
площадь окружности будет иметь имя круг и иметь два аргумента: R – радиус круга, S – вычисленная площадь. При выполнении
программы сначала вычисляется квадрат радиуса как произведение
, где R – радиус круга. Предикат, который выполняется, если найдена
площадь окружности будет иметь имя круг и иметь два аргумента: R – радиус круга, S – вычисленная площадь. При выполнении
программы сначала вычисляется квадрат радиуса как произведение 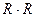 с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3). Для вычисления этого произведения
стандартный предикат вызывается со
следующим набором аргументов
УМНОЖЕНИЕ(R,R,X), где R – радиус круга, X – результат выполнения умножения. Далее полученное
произведение умножается на p=3,14159. Для этого сначала
вызывается предикат PI(Y), а затем — тот же стандартный предикат: УМНОЖЕНИЕ(Y,X,S) (S –вычисленная площадь круга).
с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3). Для вычисления этого произведения
стандартный предикат вызывается со
следующим набором аргументов
УМНОЖЕНИЕ(R,R,X), где R – радиус круга, X – результат выполнения умножения. Далее полученное
произведение умножается на p=3,14159. Для этого сначала
вызывается предикат PI(Y), а затем — тот же стандартный предикат: УМНОЖЕНИЕ(Y,X,S) (S –вычисленная площадь круга).
Длина окружности
вычисляется по формуле 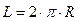 , где R – радиус окружности. Предикат, который выполняется, если
найдена длина окружности будет иметь имя окружность и два аргумента: R – радиус окружности, L – вычисленная длина окружности. При
выполнении программы сначала вычисляется произведение
, где R – радиус окружности. Предикат, который выполняется, если
найдена длина окружности будет иметь имя окружность и два аргумента: R – радиус окружности, L – вычисленная длина окружности. При
выполнении программы сначала вычисляется произведение 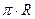 с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных между
собой соотношением Арг1*Арг2=Арг3 (предварительно вызывается предикат PI(X)). Далее полученное произведение удваивается.
с помощью стандартного
предиката УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеющего три аргумента, связанных между
собой соотношением Арг1*Арг2=Арг3 (предварительно вызывается предикат PI(X)). Далее полученное произведение удваивается.
По известной длине
окружности можно найти ее радиус воспользовавшись формулой 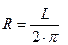 . Однако это невозможно сделать с помощью ранее описанного
предиката окружность, так как в ходе его выполнения будет вызван стандартный
предикат с двумя не конкретизированными переменными в качестве аргументов
УМНОЖЕНИЕ(X,R,Y), что приведет к ошибке в программе. Поэтому для вычисления радиуса
окружности по ее длине предикат окружность модифицируется. Для этого вводиться
дополнительная проверка, какая из переданных переменных (радиус или длина
окружности) конкретизирована некоторым
значением. Для этого используется еще один стандартный предикат ПЕР (Арг1),
который истинен, если Арг1 – не конкретизированная переменная, а иначе ложен.
Таким образом в программе появляется два правила вместо одного.
. Однако это невозможно сделать с помощью ранее описанного
предиката окружность, так как в ходе его выполнения будет вызван стандартный
предикат с двумя не конкретизированными переменными в качестве аргументов
УМНОЖЕНИЕ(X,R,Y), что приведет к ошибке в программе. Поэтому для вычисления радиуса
окружности по ее длине предикат окружность модифицируется. Для этого вводиться
дополнительная проверка, какая из переданных переменных (радиус или длина
окружности) конкретизирована некоторым
значением. Для этого используется еще один стандартный предикат ПЕР (Арг1),
который истинен, если Арг1 – не конкретизированная переменная, а иначе ложен.
Таким образом в программе появляется два правила вместо одного.
Описанная программа,
осуществляющая вычисление площадей параллелограмма, трапеции, треугольника,
круга, а также длины окружности по радиусу и радиуса по длине окружности, будет иметь вид:
PI(3.14159);
ДЕЛЕНИЕ(x,y,z)<-УМНОЖЕНИЕ(z,y,x);
треугольник(a,h,S)<-УМНОЖЕНИЕ(a,h,X),ДЕЛЕНИЕ(X,2.0,S);
параллелограмм(a,h,S)<-
УМНОЖЕНИЕ(a,h,S);
трапеция(a,b,h,S)<-СЛОЖЕНИЕ(a,b,X),УМНОЖЕНИЕ(X,h,Y),
ДЕЛЕНИЕ(Y,2.0,S);
круг
(R,S)<-УМНОЖЕНИЕ(R,R,X),PI(Y),УМНОЖЕНИЕ(Y,X,S);
окружность(R,L)<-ПЕР(L),PI(X),УМНОЖЕНИЕ(X,R,Y),УМНОЖЕНИЕ(2,Y,L);
окружность(R,L)<-ПЕР(R),PI(X),УМНОЖЕНИЕ(2,Y,L),УМНОЖЕНИЕ(X,R,Y);
Использованные
для арифметических вычислений стандартные предикаты СЛОЖЕНИЕ и УМНОЖЕНИЕ в
качестве аргументов могут иметь как целочисленный, так и вещественный тип,
значит, аргументы предикатов вычисления площадей и длины окружности могут быть
и целочисленными и вещественными. Однако для вычисления площади круга, длины
окружности и радиуса используется число p, которое может быть определено
только в некотором приближении. В программе p задано с точностью до четвертого
знака после запятой и равно 3,14159.
Следовательно, полученные результаты площади круга, длины окружности и радиуса
будут иметь такую же точность.
В
качестве примера приведем вычисление следующих параметров:
§ площади треугольника с основанием 10
и высотой 4.7;
§ площади параллелограмма со стороной
2,3 и высотой 6;
§ площади трапеции с основаниями 10, 6
и высотой 3.3;
§ площади круга радиуса 10;
§ длина окружности радиуса 10;
§ радиуса окружности с длиной 62.
Для этого системе Пролог-Д задаются
вопросы:
?треугольник(10,4.7,T);
?параллелограмм(2.3,6,P);
?трапеция(10,6,3.3,S);
?круг(10,K);
?окружность(10,L);
?окружность(R,62);
Ответ системы Пролог-Д:
T=23.5
P=13.8
S=26.4
K=314.159
L=62.8318
R=9.86761
Рекурсия
Рекурсия является мощным методом
программирования. В языке Пролог-Д она приобретает используется особенно
широко, так как в нем отсутствуют циклические конструкции. С помощью рекурсии
можно решать широкий класс задач, в том числе и простейших математических,
таких, как вычисление суммы ряда, наибольшего общего делителя, наименьшего
общего кратного .
2.3.2.Написать на
языке Пролог-Д базу знаний, описывающую вычисление сумы чисел натурального
ряда.
Для
математических вычислений в программе использовались стандартные предикаты СЛОЖЕНИЕ (Арг1, Арг2,
Арг3), УМНОЖЕНИЕ (Арг1, Арг2, Арг3),
также с их помощью были введены вспомогательные предикаты.
Стандартный
предикат СЛОЖЕНИЕ (Арг1, Арг2, Арг3), имеет три аргумента, связанных формулой
Арг1+Арг2=Арг3. Веденный с его помощью предикат ВЫЧИТАНИЕ (Арг1, Арг2, Арг3)
также имеет три аргумента, связанных по формуле Арг1-Арг2=Арг3. Стандартный
предикат УМНОЖЕНИЕ (Арг1, Арг2, Арг3), имеет три аргумента, связанных формулой
Арг1*Арг2=Арг3. С помощью этого предиката был введен еще один вспомогательный
предикат ДЕЛЕНИЕ(Арг1, Арг2, Арг3), его аргументы связаны формулой
Арг1/Арг2=Арг3:
ВЫЧИТАНИЕ(x,y,z)<-СЛОЖЕНИЕ(y,z,x);
ДЕЛЕНИЕ(x,y,z)<-УМНОЖЕНИЕ(z,y,x);
Также
из стандартных предикатов были использованы предикаты БОЛЬШЕ(Арг1, Арг2) и
НЕ(Арг1). Предикат БОЛЬШЕ имеет два аргумента Арг1 и Арг2. Этот предикат
истинен, если Арг1 > Арг2. Аргументом встроенного предиката НЕ является
предикат, если этот предикат-аргумент ложен, то предикат НЕ истинный, и
наоборот.
Предикат, который
выполняется, если найдена сумма чисел натурального ряда будет иметь имя ряд и
два аргумента: длина ряда n и значение суммы S. Для вычисления сумму чисел
натурального ряда используются следующие соображения. Во-первых, сумма ряда, состоящего из 0 элементов равна
0. Во-вторых, для того, чтобы посчитать сумму ряда длиной в n чисел надо к сумме ряда, состоящего
из (n-1) чисел, прибавить n. Второе утверждение реализуется с помощью рекурсивного
вызова. На Прологе-Д это правило выглядит следующим образом:
ряд(n,S)<-ВЫЧИТАНИЕ(n,1,m),ряд(m,X),СЛОЖЕНИЕ(n,X,S);
2.3.4. Описать
вычисление наименьшего общего кратного.
Для вычисления наименьшего общего кратного воспользуемся алгоритмом
Евклида, согласно которому НОК(x,y)=(x*y)/НОД(x,y), где x, y – натуральные числа, НОД(x,y)- наибольший общий делитель этих
чисел, НОК(x,y) – наименьшее общее кратное. А для поиска наибольшего общего делителя выполняются
следующие действия:
§ Вычислим r - остаток от деления числа
a на b, a = bq+r, 0 ≤ r < b.
§ Если r = 0, то b есть искомое число.
§ Если r ¹ 0, то заменим пару чисел (a, b)
парой (b, r)
и перейдем к первому шагу.
Для определения остатка от деления двух
чисел был введен дополнительный предикат с именем остаток и тремя аргументами: делимым,
делителем и остатком от деления. Вычисление остатка от деления также выполнено
с использованием рекурсии. В его основе лежит следующее утверждение: чтобы
получить остаток от деления числа a на число b, нужно последовательно отнимать
значение b от a до тех пор, пока полученный результат не стане меньше b. Он и будет являться остатком от
деления a на b. В прологе этот алгоритм осуществляется в следующих двух правилах:
ОСТАТОК(a,b,r)<-БОЛЬШЕ(b,a),РАВНО(r,a);
ОСТАТОК(a,b,r)<-НЕ(БОЛЬШЕ(b,a)),ВЫЧИТАНИЕ(a,b,X),ОСТАТОК(X,b,r);
В целом программа, вычисляющая сумму
натурального ряда и наименьшее общее кратное, будет иметь вид:
ВЫЧИТАНИЕ(x,y,z)<-СЛОЖЕНИЕ(y,z,x);
ДЕЛЕНИЕ(x,y,z)<-УМНОЖЕНИЕ(z,y,x);
ряд(0,0)<-!;
ряд(n,S)<-ВЫЧИТАНИЕ(n,1,m),ряд(m,X),СЛОЖЕНИЕ(n,X,S);
ОСТАТОК(a,b,r)<-БОЛЬШЕ(b,a),РАВНО(r,a);
ОСТАТОК(a,b,r)<-НЕ(БОЛЬШЕ(b,a)),ВЫЧИТАНИЕ(a,b,X),ОСТАТОК(X,b,r);
НОД(a,0,a)<-!;
НОД(a,b,n)<-БОЛЬШЕ(a,b),ОСТАТОК(a,b,X),НОД(b,X,n);
НОД(a,b,n)<-БОЛЬШЕ(b,a),ОСТАТОК(b,a,X),НОД(a,X,n);
НОК(a,b,n)<-УМНОЖЕНИЕ(a,b,X),НОД(a,b,Y),ДЕЛЕНИЕ(X,Y,n);
Примером работы программы
может служить нахождение суммы ряда: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11; и поиск
наименьшего общего кратного чисел 51 и 18.
Для этого системе
Пролог-Д задаются следующие вопросы:
?ряд(11,S);
?НОК(51,18,N);
Ответ системы Пролог-Д:
S=66
N=306
Графические
возможности системы Пролог-Д
Графические возможности системы Пролог-Д, очевидно, могут
быть использованы в рамках решения различных задач: внутри экспертных систем,
для вывода пользователю полученных результатов, при создании пользовательских
интерфейсов. Все графические построения ведутся с использованием стандартных
предикатов.
2.4.2. Используя
рекурсивное определение, напишите базу знаний, описывающую многоэтажный дом.
В программе использованы стандартные
предикаты СЛОЖЕНИЕ(Арг1,Арг2,Арг3), ЛИНИЯ(Арг1,Арг2,Арг3,Арг4,Арг5),
ЗАКРАСКА(Арг1,Арг2,Арг3,Арг4) и ЗАПИСЬ_В("grp:"). Аргументы
стандартного предиката СЛОЖЕНИЯ связаны сежду собой по формуле Арг1+Арг2=Арг3.
Исходя из этого, сумма c=a+b может быть вычислена вызовом стандартного предиката СЛОЖЕНИЕ в
виде СЛОЖЕНИЕ(a,b,c), а разность c=a-b: СЛОЖЕНИЕ(c,b,a). Предикат ЛИНИЯ позволяет построить отрезок с начальной точкой (Арг1,
Арг2), конечной (Арг3, Арг4) и цветом Арг5. Процедурно предикат
ЗАКРАСКА(Арг1,Арг2,Арг3,Арг4) означает: закрасить цветом Арг3 внутри контура с
цветом Арг4, начиная с точки (Арг1, Арг2).Предикат ЗАПИСЬ_В("grp:")
открывается файл графического вывода.
В программе были использованы
дополнительные предикаты:
§ предикат ТРЕУГОЛЬНИК(x,y,a,h) для
построения равностороннего треугольника по координате левой точки его основания
(x,y),
длине основания a и высоте h;
§ предикат ПРЯМОУГОЛЬНИК(x, y, a, h)
для построения прямоугольника по координате его левого нижнего угла (x,y),
ширине a и высоте h;
§ предикат окно(x,y) рисует контуры
четырех окон на этаже и закрашивает их
синим цветом, (x,y) – координата левого нижнего угла этажа;
§ предикат окно_дверь(x,y) предназначен
для рисования первого этажа. Рисует контуры двух окон, закрашивает их синим
цветом, рисует дверь, закрашивая ее серым цветом ((x,y) – координата левого нижнего угла
этажа);
§ предикат балкон(x,y) рисует контуры
балконов слева и справа от этажа, координата левого нижнего угла которого равна
(x,y);
§ предикат этаж(x,y) рисует контур этажа, окна и балкон,
вызывая последовательно предикаты ПРЯМОУГОЛЬНИК(x,y,200,60), окно (x,y), балкон (x,y);
§ предикат превый_этаж(x,y) рисует первый этаж дома, вызывая
последовательно предикаты ПРЯМОУГОЛЬНИК(x,y,200,60), окно_дверь(x,y);
§ предикат крыша(x,y) рисует крышу с помощью предиката
треугольник по заданной координате левого верхнего угла верхнего этажа;
Для рекурсивного построения
используется предикат дом(x,y,n),(x,y – координаты левого верхнего угла
последнего этажа, n – количество этажей), который сначала рисует верхний этаж, а затем
строит здание с n-1 этажом. Если аргумент n=1, то строиться первый этаж дома. Для конечного построения
дома используется предикат старт(n) (n – количество). Этот предикат сначала открывает файл
графического вывода, далее рисует крышу здания и само здание дома.
Все вышеизложенное реализовано в
следующей программе:
Описанные утверждения реализованы в
нижеприведенной программе:
ТРЕУГОЛЬНИК(x,y,a,h)<-СЛОЖЕНИЕ(x,a,r),УМНОЖЕНИЕ(X,2,a),
СЛОЖЕНИЕ(x,X,s),СЛОЖЕНИЕ(u,h,y),
ЛИНИЯ(x,y,r,y,1),ЛИНИЯ(x,y,s,u,1),
ЛИНИЯ(r,y,s,u,1);
ПРЯМОУГОЛЬНИК(x,y,a,h)<-СЛОЖЕНИЕ(x,a,r),СЛОЖЕНИЕ(u,h,y),
ЛИНИЯ(x,y,r,y,1),ЛИНИЯ(x,y,x,u,1),
ЛИНИЯ(x,u,r,u,1),ЛИНИЯ(r,u,r,y,1);
окно(x,y)<-СЛОЖЕНИЕ(u,15,y),СЛОЖЕНИЕ(x,30,r),СЛОЖЕНИЕ(x,70,s),
СЛОЖЕНИЕ(x,110,t),СЛОЖЕНИЕ(x,150,p),
ПРЯМОУГОЛЬНИК(r,u,20,30),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(90,a,1,1),
ПРЯМОУГОЛЬНИК(s,u,20,30),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(130,a,1,1),
ПРЯМОУГОЛЬНИК(t,u,20,30),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(170,a,1,1),
ПРЯМОУГОЛЬНИК(p,u,20,30),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(210,a,1,1);
балкон(x,y)<-СЛОЖЕНИЕ(r,20,x),СЛОЖЕНИЕ(x,200,s),
ПРЯМОУГОЛЬНИК(r,y,20,20),ПРЯМОУГОЛЬНИК(s,y,20,20);
окно_дверь(x,y)<-СЛОЖЕНИЕ(u,15,y),СЛОЖЕНИЕ(x,30,r),
СЛОЖЕНИЕ(x,150,s),
СЛОЖЕНИЕ(x,86,t),
ПРЯМОУГОЛЬНИК(r,u,20,30),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(90,a,1,1),
ПРЯМОУГОЛЬНИК(s,u,20,30),
ЗАКРАСКА(210,a,1,1),
ПРЯМОУГОЛЬНИК(t,y,28,40),
СЛОЖЕНИЕ(a,25,y),
ЗАКРАСКА(150,a,7,1);
этаж(x,y)<-ПРЯМОУГОЛЬНИК(x,y,200,60),окно(x,y),балкон(x,y);
первый_этаж(x,y)<-ПРЯМОУГОЛЬНИК(x,y,200,60),окно_дверь(x,y);
крыша(x,y)<-СЛОЖЕНИЕ(r,10,x),ТРЕУГОЛЬНИК(r,y,220,40);
дом(x,y,1)<-первый_этаж(x,y);
дом(x,y,n)<-этаж(x,y),СЛОЖЕНИЕ(y,60,u),СЛОЖЕНИЕ(m,1,n),дом(x,u,m);
старт(n)<-ЗАПИСЬ_В("grp:"),крыша(50,60),дом(50,120,n);
В качестве примера приведем результат
выполнения программы для двух случаев: построения одноэтажного и шестиэтажного
дома. Для этого нужно созданной базе знаний задать вопросы: ?старт(1) и
?старт(6) (рис. 2, 3).
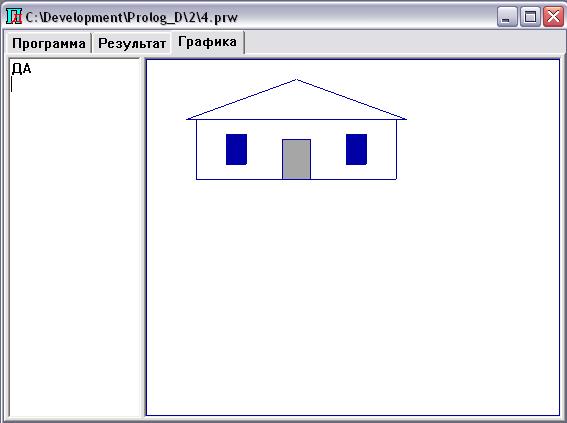
Рис. 2
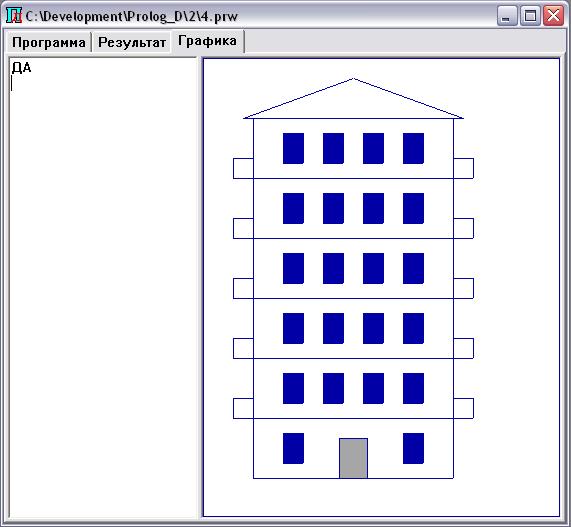
Рис. 3
Обработка
списков
Задачи, связанные с обработкой списков встречаются довольно часто на
практике, когда необходимо составить перечень чего-либо.
2.5.2. Напишите базу знаний,
описывающую обращение списка (первый элемент становиться последним).
Обращение списка можно
представить в виде переписывания его
элементов, начиная с головы списка, в
голову другого списка, который был в начале пустым.
Такую задачу можно
списать с помощью следующих выражений:
- основная ситуация состоит в том, что
если в хвост пустого списка дописать некоторый список, то результат будет равен
второму списку.
- рекурсивна ситуация состоит в том,
что первый список будет в обратном порядке дописан ко второму, если его голова
будет добавлена в голову второго списка,
а его хвост будет в обратном порядке дописан к измененному второму
списку.
Эти выражения реализуются в предикате
ОБРАТИТЬ(Арг1, Арг2, Арг3) с тремя аргументами, где Арг1 – исходный список, Арг2 – список, к
которому дописываются элементы, Арг3 – результирующий список.
В программе также
присутствует еще два предиката. Первый из них предназначен для переписывания
головы первого списка в голову второго. Этот предикат имеет имя ДОБАВИТЬ и тру
аргумента: ДОБАВИТЬ (Арг1, Арг2, Арг3), где Арг1 – первый список, Арг2 –
список, к которому необходимо дописать голову первого списка, Арг3 – измененный
второй список.
Второй предикат предназначен для запуска программы: старт(R,S), где R – исходный список, S – результирующий список. Этот
предикат является стартом рекурсии. Он вызывает предикат ОБРАТИТЬ с
аргументами, инициализированными следующим образом: ОБРАТИТЬ (R,[],S).
Описанные утверждения будут иметь вид следующей
программы:
ДОБАВИТЬ(X,Y,[X|Y]);
ОБРАТИТЬ([],Y,Y);
ОБРАТИТЬ([X|T],Y,S)<-ДОБАВИТЬ(X,Y,Z),
ОБРАТИТЬ(T,Z,S);
старт(R,S)<-ОБРАТИТЬ(R,[],S);
В качестве примера
обратим список [13,7,6,1,14,65,2]. Для этого к созданной базе знаний нужно
задать вопрос ?старт([13,7,6,1,14,65,2],S);
Ответ системы Пролог-Д
будет
S=[2,65,14,1,6,7,13]
Заключение
В ходе выполнении работы
на языке Пролог-Д были созданы базы знаний для отдельных заданий. Базы
знаний реализовывались с использованием
таких понятий, как факты, правила, рекурсия. Для выполнения отдельных подзадач
использовались стандартные предикаты системы Пролог-Д, в том числе стандартные
предикаты арифметических действий и стандартные предикаты работы с графикой. В
качестве отдельных структур данных был рассмотрен список.
По своей сути,
выполненные задания в настоящей работе представляют из себя системы
искусственного интеллекта, т.е. каждое задание – это программная система,
имитирующая на компьютере мышление человека. Каждое задание выдержано в рамках определениюя
Комитета по Экспертным Системам Британского Компьютерного Общества, согласно
которому под экспертной системой
понимается «воплощение в ЭВМ компонента опыта эксперта, основанного на знании,
в такой форме, что машина может дать интеллектуальный
совет или принять интеллектуальное
решение относительно обрабатываемой функции». Для создания такой системы
необходимо изучать процесс мышления человека, решающего определенные задачи или
принимающего решения в конкретной области, выделить основные шаги этого
процесса и разработать программные средства, воспроизводящие их на компьютере.
Система искусственного
интеллекта, созданная для решения задач –экспертная система – имеет источником
знаний мнения экспертов в соответствующей предметной области. Поскольку
экспертные системы основываются исключительно на человеческом опыте, с полной
определенностью никогда нельзя сказать, что их выводы абсолютно верны, поэтому
в экспертных системах широко применяются теория вероятностей и нечеткая логика.
Список литературы
1. Абдикеев Н.М. Проектирование
интеллектуальных систем в экономике. Учебник/М.: Экзамен, 2004, - 526с.
2. Алексеев М.Н., Бешенков С.А., Гейн
А.Г., Григорьев С.Г. Информатика и информационные технологии: практические работы
/ Миасс, 2000 – 42с.
3. Братко И. Программирование на языке
Пролог для искуственого интеллекта: Пер. с англ. / М.: Мир, 1990 – 560 с.
4. Доорс Дж., Рейблейн А., Вадера С.
Пролог – язык программирования будущего / М.: Финансы и статистика, 1990 – 144
с.
5. Гаврилова Т.А., Хорошевский В.Ф. Базы
знаний интеллектуальных систем. Учебник / С-П.:Питер, 2000 – 382 с.
6. Романов В.П. Интеллектуальные
информационные системы в экономике. Учебник / М:. Экзамен, 2003 – 494 с.