Задача 4

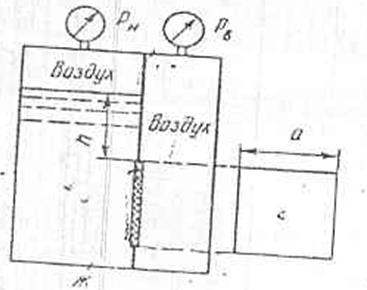
Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а=400 мм, закрытое крышкой. Давление над жидкостью Ж (керосин) в левой части резервуара определяется показателем манометра Р_м = 0,07 МПа (абс); давление воздуха в правой части – показателем мановаккуумметра Р_в = 0,02 МПа (абс). Определить величину и точку приложения результирующей силы давления на крышку. Расстояние от поверхности жидкости до крышки h=1300 мм.

Указание: Эксцентриситет центра давления для результирующей силы:

.

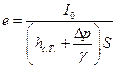Решение:

Геометрический центр крышки находится от поверхности жидкости на расстоянии h + a/2.

Давление керосина на этой глубине.

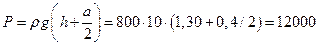Па.

Тогда величина результирующей силы давления:

.

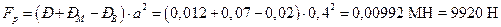Эксцентриситет центра давления для результирующей силы:

м.

Точка приложения результирующей силы к крышке находится на высоте h+a/2+е=1,3+0,2+0,0017=1,5017 м.

Задача 14

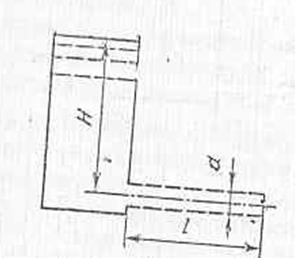
Определить длину трубы  l, при которой расход жидкости из бака будет ровно в два раза меньше, чем через отверстие того же бака диаметра  d = 70 мм. Напор над отверстием равен  Н = 4 м. Коэффициент гидравлического трения .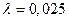

Решение:

По формуле Торричелли, расход жидкости через отверстие площадью  s  равен 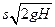. Если делать поправку на сопротивление по длине, то формула Торричелли изменится: .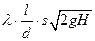

Так как, по условию задачи, расход жидкости из бака будет ровно в два раза меньше, чем через отверстие того же бака, то выразим искомую длину трубы из уравнения:

=.

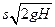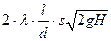Откуда искомая длина 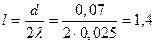 м.

Задача 20

Вода в количестве Q перекачивается по чугунной  трубе диаметром d, длиной l c толщиной стенки d. Свободный конец трубы снабжен затвором. Определить время закрытия затвора при условии, чтобы повышение давления в трубе при закрытии затвора не превышало 10 атмосфер. Как повысится давление при мгновенном закрытии затвора?

Решение:

Скачок давления распространяется по трубе в виде упругой волны со скоростью u, определяемой коэффициентом сжимаемости и плотностью жидкости, модулем упругости материала трубы, ее диаметром и толщиной стенок. Для потоков воды в стальных и чугунных трубах  u ” 1000 – 1350 м/с.

Если жидкость плотности  ?  течет со скоростью  v  в трубопроводе с площадью сечения  S  , а задвижка в конце трубопровода закрывается за время (?t)_з, то возникает увеличение давления  ?p  . В прилегающем к задвижке слое жидкости длиной  ?l= u(?t)_з и массой  m=?S?l, теряется импульс ?(mv)=?S?lv. По второму закону Ньютона изменение импульса определяется величиной действующей силы: ?(mv)/ (?t)_з = F. Учитывая, что  F =?pS , получаем выражение для величины скачка давления:

                                               ?p = ?vu    

Образующееся при гидравлическом ударе повышение давления распространяется против течения жидкости и  через время  L/u  ( L-длина трубопровода) достигает резервуара. Здесь давление падает, и это падение давления передается обратно к задвижке с той же скоростью в виде отраженной волны (волна понижения). Циклы повышений и понижений давления чередуются через промежутки времени  3L/u при условии троекратного скачка давления, пока этот колебательный процесс не затухнет из-за потерь энергии на трение и деформацию стенок. Эта формула   действительна лишь в случае, когда время закрытия запорного устройства сравнительно мало, т.е. при условии (?t)_з < 3L/u. При (?t)_з > 3L/u отраженная волна придет к запорному устройству раньше, чем задвижка закроется, и повышение давления в трубопроводе уменьшится. Из этого условия и найдем время, точнее установим, что время должно быть меньше следующей величины:

(?t)_з < 3L/u.

(?t)_з < 3 ∙ 0,7 ∙ 1,7 м / 1000 (м/с).

(?t)_з <0,00357 с.

Задача 24

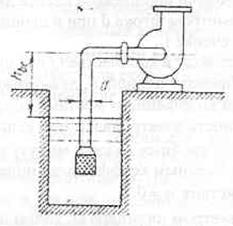
Центробежный насос производительностью Q=22 л/с работает при частоте вращения  п=2890 об/мин. Определить допустимую высоту всасывания, если диаметр всасывающей трубы d=125 мм, а ее длина l=3 м. Коэффициент кавитации в формуле Руднева принять равным  С=900. Температура воды t=20°С. Коэффициент сопротивления колена 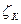=0,2. Коэффициент сопротивления входа в трубу =1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.

Решение:

Расход воды рассчитывается по формуле:

.

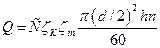Выразим из этой формулы искомую величину (высоту) и подставим исходные данные задачи, учитывая, что 22 л/с равен 0,022 м³/с:

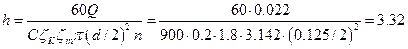 м.

Ответ: 3,32 м.

Задача 29

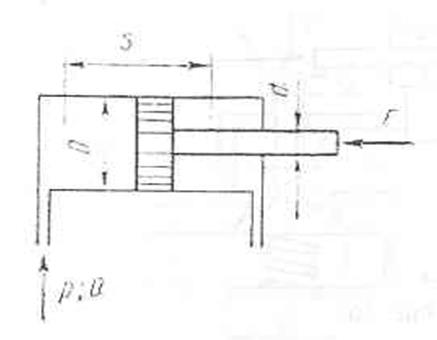
Поршневой насос простого действия с диаметром цилиндра D=70 мм, ходом поршня S=240 мм, числом двойных ходов в минуту п=70 ход/мин и объемным КПД h_об=0,9 подает рабочую жидкость в систему гидропровода. При какой частоте вращения должен работать включенный параллельно шестеренный насос с начальным диаметром шестерен d=56 мм, шириной шестерен b=5 мм, числом зубьев z=30 и объемным КПД  h_об=0,86, чтобы количество подаваемой жидкости удвоилось?

Решение:

Поршневой насос простого действия с диаметром цилиндра D=70 мм, ходом поршня S=240 мм, числом двойных ходов в минуту п=70 ход/мин и объемным КПД h_об=0,9 подает рабочую жидкость в количестве

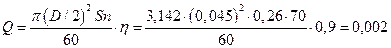 м³/мин.

Для расчета минутной подачи насосов с двумя одинаковыми шестернями можно пользоваться формулой

Q = η₀A(D_г- A)bN ,

где η₀ - объемный КПД насоса, зависящий от конструкции, технологии изготовления и давления насоса и принимаемый равным 0,7-0,95; А - расстояние между центрами шестерен, равное диаметру начальной окружности D; D_г - диаметр окружности головок зубьев; b - ширина шестерен; N - частота вращения ротора, об/мин.

Согласно условию задачи, количество подаваемой жидкости должно удвоиться, тогда искомая частота вращения:

N = η₀A(D_г-A)b / (2∙Q) = 0,9∙30∙(72-30)∙65 / (2∙0,002) = 302 об/мин.

Ответ: 302 об/мин.

Задача 40

Пользуясь характеристикой гидромуфты, определить расчетный и максимальный моменты, передаваемые ею, а также передаточное отношение, коэффициент полезного действия и скольжение при этих режимах, если активный диаметр гидромуфты D=430 см, частота вращения ведущего вала n=1800 об/мин, рабочая жидкость – трансформаторное масло. Как изменяется  передаваемые крутящий момент и мощность, если частоту вращения ведущего вала увеличить в полтора раза?

Решение:

В гидромуфте (гидропередача без внешней опоры) момент на турбине всегда равен моменту на насосе, но передача энергии в ней происходит с определенными потерями, характеризуемыми в рабочем режиме  значением  К.П.Д. Поскольку моменты колес раны, то  К.П.Д. численно равен отношению частоты вращения турбины n₂ к частоте вращения насоса n_1, т.е. передаточному отношению  i ( i= n₂/n₁).

Момент гидромуфты Мг  подчиняется зависимости

М = λi·ρ·(n / 60)²·D_a,       где:

λi - коэффициент момента, являющийся параметром гидромуфты данного типа при заданном значении i, ρ-плотность РЖ, Da- активный диаметр, равный наибольшему диаметру рабочей полости гидромуфты. 

Отсюда искомый активный диаметр:

D_a = М / (λi·ρ·(n / 60)²) = 350 / (60∙10^-7 ∙ 8600 ∙ (1100 / 60)²) = 0,202 м.

Построим внешнюю (моментальную) характеристику гидравлической муфты. В эту характеристику входят:

1)    момент муфты: М = 350 Н∙м;

2)    коэффициент момента λi = 60∙10^-7 мин²/м;

3)    активный диаметр: D_a = 0,202 м;

4)    частота вращения  п = 1800 об/мин.

Ответ: 350 Н∙м.