Задача 1
Определить величину и
направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня
находится воздух, слева от поршня и в резервуаре, куда опущен открытый конец
трубы – масло турбинное. Показание пружинного манометра – 100000 Па. Дано:
Н=5м, D= 160, d=80 мм.
Решение:
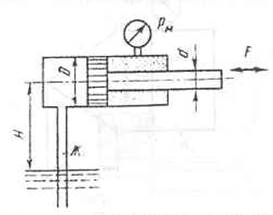
Для удержания поршня на
месте необходимо прижить силу, направленную от поршня, как показано на рисунке
жирной стрелкой. По величине эта сила должна уравновесить силу давления в 1
атм. со стороны жидкости. Сила давления жидкости
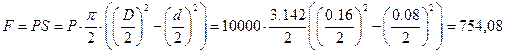Н.
Ответ: 754,08 Н;
направлена вправо от поршня.
Задача 7
При истечении жидкости из резервуара в атмосферу по
горизонтальной трубе диаметром d=40 мм и длиной 2l = 4 м. Уровень в пьезометре, установленном посередине трубы, равен h=3 м. Определить расход Q и коэффициент гидравлического трения l, если статический напор в баке постоянен и равен Н. Построить
пьезометрическую и напорную линии. Сопротивлением жидкости в труб пренебречь.
Решение:
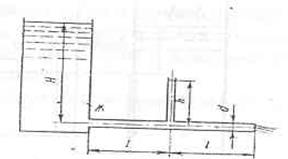
Искомый расход с учетом потерь в соединительных трубах
находится по формуле
.
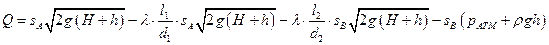Выполним элементарные преобразования с этой формулой:
.
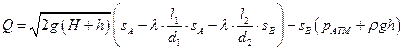Подставим числовые значения:
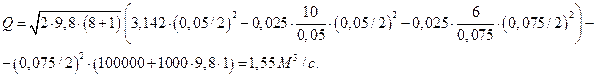
Для построения пьезометрических линий, найдем
пьезометрические высоты соответственно в точках А и В:
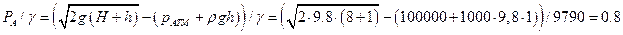м.
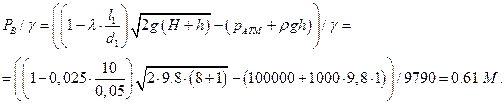
Тогда пьезометрическая линия выглядит следующим образом:
Задача 10
Определить диаметр трубопровода, по которому попадает
жидкость Ж с расходом Q, из условия получения в нем максимально возможной скорости при
сохранении ламинарного режима. Температура жидкости t = 20° C.
Решение:
Выражая скорость течения жидкости из формулы для расхода
воды, принимая во внимание условие перехода от ламинарного к турбулентному
течению, получаем:
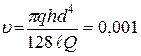м2/с = 10 см2/с.
Ответ: 10 см2/с.
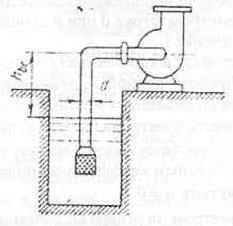
Задача 22
Центробежный насос
производительностью Q=22 л/с работает при частоте вращения
п=2890 об/мин. Определить допустимую высоту всасывания, если диаметр
всасывающей трубы d=125 мм, а ее длина l=3 м. Коэффициент кавитации в формуле Руднева принять
равным С=900. Температура воды t=20°С. Коэффициент сопротивления колена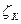 
=0,2. Коэффициент сопротивления входа в трубу 
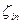=1,8. Эквивалентная шероховатость стенок трубы R=0,15 мм.
Решение:
Расход воды
рассчитывается по формуле:
.
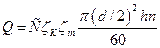Выразим из этой формулы
искомую величину (высоту) и подставим исходные данные задачи, учитывая, что 22
л/с равен 0,022 м3/с:
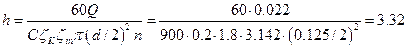м.
Ответ: 3,32 м.
Задача 28
Определить средний
объемный коэффициент полезного действия, максимальную теоретическую подачу и
степень неравномерности подачи поршневого насоса двойного действия и диаметром
цилиндра D = 100 мм, ходом поршня S = 60 мм, диаметром штока d = 25 мм, при n = 60 (об/мин) двойных ходах в
минуту, заполняющего мерный бак W = 0.077 м3 за
t = 100 с.
Решение:
Действительная
производительность насоса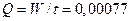 
м3/сек. Максимальная
теоретическая производительность насоса двойного действия будет
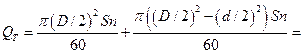
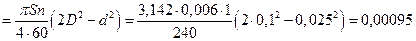м3/сек.
Отношение
действительной подачи Q к
теоретической QT
называется объемным КПД поршневого насоса:
.
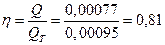Степень неравномерности
подачи насоса можно принять для одноцилиндрового – 3,14, а для двухцилиндрового
– 1,57.
Задача 21
Определить время закрытия
задвижки, установленной на свободном конце стального водопровода диаметром d=150 мм, длиной l = 1700 м, с толщиной стенки d=8 мм,
при условии, чтобы максимальное повышение давления в водопроводе было в три
раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после
мгновенного закрытия задвижки повышение давления распространится до сечения,
находящегося на расстоянии 0,7l от задвижки?
Решение:
Скачок давления
распространяется по трубе в виде упругой волны со скоростью u, определяемой
коэффициентом сжимаемости и плотностью жидкости, модулем упругости материала
трубы, ее диаметром и толщиной стенок. Для потоков воды в стальных и чугунных
трубах u ” 1000 – 1350 м/с.
Если жидкость
плотности ?
течет со скоростью v в трубопроводе с площадью сечения S , а
задвижка в конце трубопровода закрывается за время (?t)з, то возникает
увеличение давления ?p
. В прилегающем к задвижке слое жидкости длиной ?l= u(?t)з и массой m=?S?l, теряется импульс ?(mv)=?S?lv. По второму закону Ньютона
изменение импульса определяется величиной действующей силы: ?(mv)/ (?t)з = F. Учитывая,
что F =?pS , получаем выражение для величины
скачка давления:
?p = ?vu
Образующееся при
гидравлическом ударе повышение давления распространяется против течения
жидкости и через время L/u (
L-длина трубопровода) достигает резервуара. Здесь давление падает, и это
падение давления передается обратно к задвижке с той же скоростью в виде
отраженной волны (волна понижения). Циклы повышений и понижений давления
чередуются через промежутки времени 3L/u
при условии троекратного скачка давления, пока этот колебательный процесс не
затухнет из-за потерь энергии на трение и деформацию стенок. Эта формула действительна лишь в случае, когда время
закрытия запорного устройства сравнительно мало, т.е. при условии (?t)з < 3L/u. При (?t)з > 3L/u отраженная
волна придет к запорному устройству раньше, чем задвижка закроется, и повышение
давления в трубопроводе уменьшится. Из этого условия и найдем время, точнее установим,
что время должно быть меньше следующей величины:
(?t)з < 3L/u.
(?t)з < 3 ∙ 0,7
∙ 1,7 м / 1000 (м/с).
(?t)з <0,00357 с.