Министерство образования РФ
Всероссийский заочный
финансово-экономический институт
Кафедра Экономико-математических методов и
моделей
КОНТРОЛЬНАЯ
РАБОТА
по
дисциплине «Эконометрика»
Вариант
8
Исполнитель:
Специальность:
Группа:
№ зачетной книжки:
Руководитель:
Курск 2008
Задача
По предприятиям легкой промышленности региона получена информация, характеризующая
зависимость объема выпуска продукции (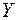 , млн. руб.) от объема капиталовложений (
, млн. руб.) от объема капиталовложений (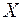 , млн. руб.)
, млн. руб.)
|
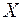
|
17
|
22
|
10
|
7
|
12
|
21
|
14
|
7
|
20
|
3
|
|
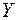
|
26
|
27
|
22
|
19
|
21
|
26
|
20
|
15
|
30
|
13
|
Требуется:
1.
Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
2.
Вычислить остатки; найти остаточную сумму квадратов;
оценить дисперсию остатков  ; построить график остатков.
; построить график остатков.
3.
Проверить выполнение предпосылок МНК.
4.
Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия
Стьюдента 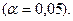
5.
Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью 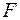 - критерия Фишера
- критерия Фишера 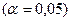 , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6.
Осуществить прогнозирование среднего значения
показателя 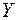 при уровне
значимости
при уровне
значимости 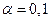 , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
7.
Представить графически: фактические и модельные
значения 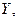 точки прогноза.
точки прогноза.
8.
Составить уравнения нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных уравнений регрессии.
9.
Для указанных моделей найти коэффициенты детерминации,
коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
Решение
Рассмотрим зависимость объема
выпуска продукции (Y,
млн. руб.) от объема капиталовложений (X, млн. руб.) на 10 предприятиях легкой промышленности (n=10).
|
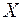
|
17
|
22
|
10
|
7
|
12
|
21
|
14
|
7
|
20
|
3
|
|
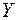
|
26
|
27
|
22
|
19
|
21
|
26
|
20
|
15
|
30
|
13
|
Рассчитаем выборочный коэффициент корреляции по формуле (использована функция КОРРЕЛ Мастера функций
Excel):

Коэффициент корреляции положительный, это
свидетельствует о наличии прямой статистической связи, то есть с увеличением x – y в сущности увеличивается.
Оценим значимость полученного
коэффициента с помощью t-критерия
Стьюдента.
Расчетное значение t-критерия определяем по
формуле:
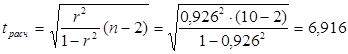
Табличное
значение t-критерия
определяется при заданном уровне значимости α
и числе степеней свободы n-2.
tтабл.(α, n-2)
Используем стандартную функцию СТЬЮДРАСПОБР (0,05;8) Мастера функций Excel:
tтабл. = 2,306
tрасч.=6,916 > tтабл.=2,306
Значит,
коэффициент корреляции значим.
1. Найти параметры уравнения
линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
Для оценки параметров линейного уравнения парной регрессии 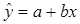 используем метод наименьших квадратов
(МНК).
используем метод наименьших квадратов
(МНК).
Для расчетов используется программа «Регрессия» надстройки «Анализ
данных» пакета Excel.
Таким образом, получим уравнение регрессии вида 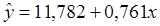 .
.
Параметр b является
коэффициентом регрессии. Он равен 0,761, то есть, с увеличением объема
капиталовложений на 1 млн. руб. объем выпускаемой продукции по предприятиям
легкой промышленности увеличится в среднем на 761 тыс. руб., что
свидетельствует об эффективности работы предприятий.
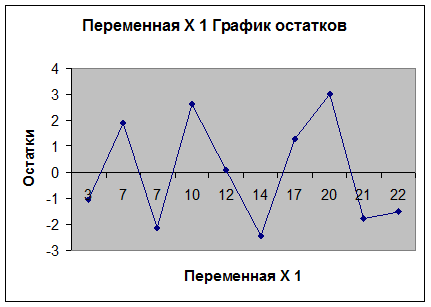
2. Вычислить остатки; найти
остаточную сумму квадратов; оценить дисперсию остатков 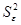 ; построить график остатков.
; построить график остатков.
Проверка адекватности построенной модели регрессии проводится на основе
анализа остатков - ei.
Остатки рассчитываются по формуле:
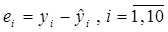
Расчет остатков произведен с помощью прикладной программы Excel в таблице «Вывод
остатка».
Остаточная сумма квадратов рассчитывается по формуле (использована функция СУММКВ Мастера функций
Excel):
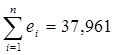
Дисперсия остатков рассчитывается по формуле (использована функция ДИСП Мастера функций
Excel):
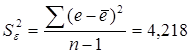
3. Проверить выполнение предпосылок МНК
Проверить
выполнение предпосылок МНК, т.е. оценить адекватность построенной модели, можно
на основе исследования свойств остатков.
1. Нулевое
или близкое к нулю среднее значение остатков.
Это
свойство означает, что ∑(yi - yi) = 0 или может быть
величиной близкой к нулю. В данной задаче просуммированные остатки равны нулю,
то есть первое свойство выполняется.
2. Случайный характер остатков.
Проверить это свойство можно на основе критерия поворотных точек. В
соответствии с этим критерием в случайном ряду остатков должно выполняться
строгое неравенство:


Поскольку P=6 больше 2, то свойство случайности остатков
выполняется.
3. Независимость остатков
(отсутствие автокорреляции).
Проверку этого свойства можно провести с помощью коэффициента автокорреляции,
который рассчитывается по формуле (использована функция КОРРЕЛ Мастера функций Excel):
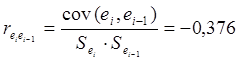
Проверим полученный коэффициент автокорреляции на значимость с помощью t-критерия Стьюдента.
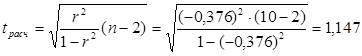
tрасч.=1,147 < tтабл.=2,306, значит коэффициент
корреляции не значим, т.е. остатки неавтокоррелированны. Это означает, что
свойство независимости остатков выполняется.
4. Соответствие ряда остатков нормальному закону распределения.
Данное свойство проверяется с помощью R/S критерия.
С помощью функции СТАНДОТКЛОН
Мастера функций Excel по таблице остатков найдем среднее квадратическое
отклонение.
Sε = 2,054
Расчетное значение этого R/S критерия
определяется по формуле:

Для данной задачи n=10 и α=0,05, значит границы интервала
равны 2,67 и 3,57. Расчетное значение R/S – критерия
попадает в интервал 2,67<2,647< 3,57, следовательно, свойство
нормальности остатков выполняется.
5. Гомоскедастичность (постоянство) дисперсии
остатков.
Для обнаружения
гетероскедастичности (то есть нарушение гомоскедастичности), используем тест
Гольдфельда-Квандта:
а)
Упорядочим выборку из n-наблюдений по мере
возрастания факторного признака x.
б) Совокупность наблюдений
разделим на 2 группы, соответственно с малыми и большими значениями факторного
признака х.
Определим по
каждой из групп уравнения регрессии:
- для первой
группы с помощью программы Регрессия
надстройки Анализ данных пакета
Excel получим
уравнение регрессии: 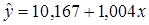
- для второй группы, так же, с помощью программы Регрессия пакета Анализ
данных в среде Excel получим уравнение регрессии: 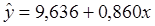
в) Вычислим остаточную сумму
квадратов:
- для первой регрессии, она
определяется по формуле (использована функция СУММКВ Мастера функций Excel):
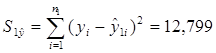
- для второй регрессии, она
определяется по формуле (использована функция СУММКВ Мастера функций Excel):
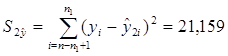
Далее используем F-критерий
Фишера. Расчетное значение этого Критерия определяется по формуле:
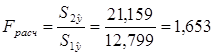
Табличное значение F-критерия
Фишера находим при помощи функции FРАСПОБР Мастера функций Excel.
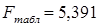
Поскольку Fрасч=1,653<Fтабл=5,391, то свойство гетероскедастичности не имеет места, т.е.
остатки обладают свойством гомоскедастичности.
Таким образом, выполняются все условия проверки (предпосылки
МНК), это значит, что построенная регрессионная модель является адекватной
реальному процессу, а, следовательно, её можно использовать для построения
прогнозных оценок.
4.
Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия
Стьюдента 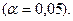
Для оценки статистической значимости,
существенности параметров модели парной регрессии 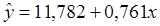 , используется t-критерий Стьюдента. Расчетные
значения t-статистики получаются путем
сопоставления значения параметров a и
b с величинами случайных ошибок этих параметров Sa и Sb:
, используется t-критерий Стьюдента. Расчетные
значения t-статистики получаются путем
сопоставления значения параметров a и
b с величинами случайных ошибок этих параметров Sa и Sb:
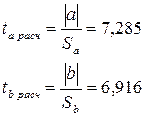
Случайные ошибки
определяются по формулам:
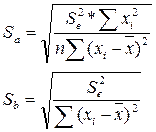
Воспользуемся результатами, полученными
программой Регрессия надстройки Анализ данных пакета Excel.
Далее, полученные расчетные
значения: 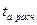 = 7,285 ;
= 7,285 ; 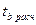 =6,916 сравниваем с табличным значением tтабл . Табличное значение t-критерия определяется при (n-2) – в нашем случае n-2=10-2=8 степеней свободы и
соответственно уровнем значимости α=0,05; рассчитаем tтабл = 2,306.
=6,916 сравниваем с табличным значением tтабл . Табличное значение t-критерия определяется при (n-2) – в нашем случае n-2=10-2=8 степеней свободы и
соответственно уровнем значимости α=0,05; рассчитаем tтабл = 2,306.
Таким образом, значение 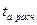 > tтабл, следовательно, параметр а значим, и
> tтабл, следовательно, параметр а значим, и 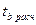 > tтабл - параметр b также значим.
> tтабл - параметр b также значим.
5. Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью 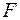 - критерия Фишера
- критерия Фишера 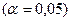 , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент
детерминации рассчитывается по формуле:
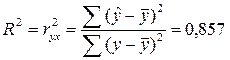
Используя программу
Регрессия надстройки Анализ данных пакета Excel, получим R-квадрат=0,857.
Таким образом,
все изменения объема выпуска продукции в среднем обусловлены на 85,7%
изменениями объема капиталовложений и на 14,3%
- изменениями факторов, неучтенных в модели.
Для проверки
значимости модели регрессии используют F-критерий Фишера. С этой целью выполняется сравнение расчетного Fрасч значения и табличного значения Fтабл критерия
Фишера.
Fрасч рассчитывают по
формуле:
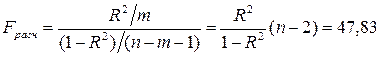
Fтабл=(α, m, n-m-1) рассчитывают с помощью
функции FРАСПОБР Мастера функций Excel:
Fтабл =5,32.
Так как, Fрасч > Fтабл , то уравнение регрессии в
целом значимо.
Оценку качества
построенной модели (её точности) даёт также средняя относительная ошибка
аппроксимации (средняя относительная ошибка модели), которая рассчитывается по
формуле:
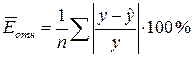
Произведем
расчеты с помощью программы Excel. Чтобы найти 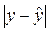 воспользуемся функцией ABS Мастера
функций Excel.
воспользуемся функцией ABS Мастера
функций Excel.
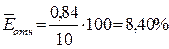 .
.
Это означает,
что в среднем расчетные значения 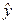 отличаются от
фактических значений на 8,40%.
отличаются от
фактических значений на 8,40%.
Так как 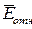 =8,40% < 10%, то ошибка считается приемлемой, что
говорит о хорошей точности модели.
=8,40% < 10%, то ошибка считается приемлемой, что
говорит о хорошей точности модели.
6.
Осуществить прогнозирование среднего значения показателя 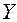 при уровне
значимости
при уровне
значимости 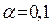 , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
Осуществим
прогнозирование при 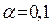 . Прогнозное значение признака y
получается при подстановке в уравнение регрессии соответствующего прогнозного
значения факторного признака x:
. Прогнозное значение признака y
получается при подстановке в уравнение регрессии соответствующего прогнозного
значения факторного признака x:
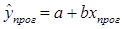
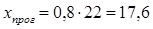
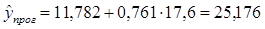
Такой прогноз называется точечным. Значение факторного признака xпрог не должно значительно отличаться от входящих в исследуемую выборку (по
которой определено уравнение регрессии). Точечный прогноз обычно сопровождают
интервальным, поскольку трудно ожидать совпадения в будущем фактического
значения y с  прог. Интервальный прогноз задается с помощью
доверительного интервала:
прог. Интервальный прогноз задается с помощью
доверительного интервала: 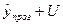 , где U –
величина отклонения от линии регрессии.
, где U –
величина отклонения от линии регрессии.
Доверительный интервал – это интервал, в котором с заданной вероятностью
можно ожидать появление фактического значения прогнозируемого показателя.
Величина U оценивается по формуле:
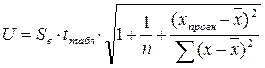
Стандартная ошибка - Se =2,178; 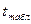 рассчитаем с помощью
программы Excel
- Мастера функций – СТЬЮДРАСПОБР (0,1;8);
его значение составит
рассчитаем с помощью
программы Excel
- Мастера функций – СТЬЮДРАСПОБР (0,1;8);
его значение составит 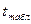 =1,86.
=1,86.
Находим
недостающие данные для расчета интервального прогноза.
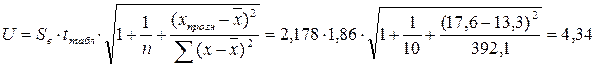
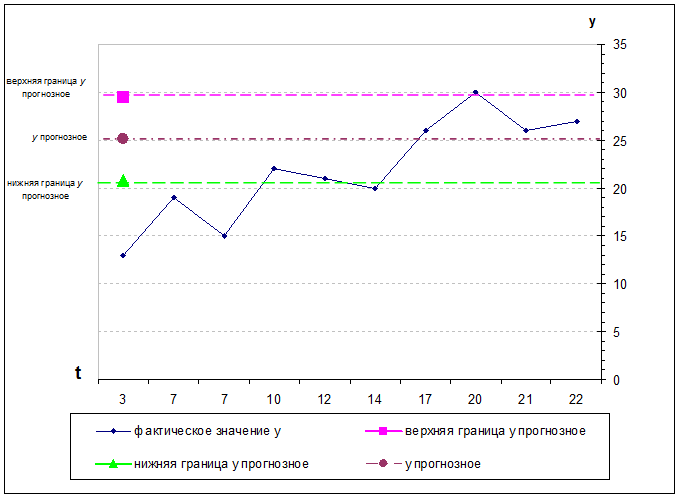
В результате имеем точечный
прогноз (25,176 ; 17,6)
Нижняя граница = 25,176-4,34=20,84
Верхняя граница =25,176+4,34=29,51
Таким образом, с вероятностью 80%
объем выпуска продукции (Y, млн.руб.) при ожидаемых
объемах капиталовложений (X, млн.руб.), будет
находиться в пределах от 20,84 млн.руб. до 29,51 млн.руб.
7. Представить графически: фактические и модельные значения  точки прогноза.
точки прогноза.
С помощью Мастер диаграмм пакета Excel
графически отразим фактические и модельные значения Y, точки прогноза.
Для этого преобразуем сформированный программой
Регрессия График подбора:
- Выберем тип диаграммы «точечная», на которой значения соединены
отрезками;
- Далее на графике изобразим результаты
прогнозирования. Для этого «кликнем» правой кнопкой мышки по точкам на графике,
и в появившемся меню выберем Исходные данные. Затем на закладке «Ряд»
нажмем кнопку «Добавить» и укажем диапазон размещения данных. Фактические
значения Y
отмечены на графике синим цветом, модельные – лиловым.
- Затем таким же образом добавляем
прогнозные значения Y.
Фактические, модельные значения Y и прогноз
8. Составить
уравнения нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных уравнений
регрессии.
а) Гиперболическая функция.
Уравнение гиперболической
функции имеет вид:
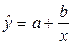
Это уравнение приводится к
линейному виду с помощью замены Z=1/x
В результате получается
линейное уравнение 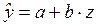
Используя
программу Регрессия надстройки Анализ данных пакета Excel, найдем
параметры этого уравнения:
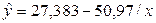
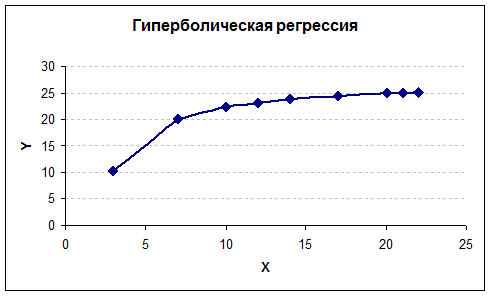
В полученное
уравнение регрессии подставим имеющиеся значения х, таким образом найдем теоретические значения у. Затем по этим данным построим график гиперболической модели регрессии
б) Степенная функция.
Уравнение степенной модели
имеет вид: 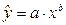
Приведем это
уравнение к линейному виду. Для этого произведем логарифмирование обеих частей
уравнения (использована функция LOG10 Мастера функций пакета Excel):
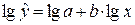
Обозначим 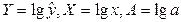 . Тогда уравнение примет вид Y=A+bX –
линейное уравнение регрессии.
. Тогда уравнение примет вид Y=A+bX –
линейное уравнение регрессии.
Используя
программу Регрессия надстройки Анализ данных пакета Excel, найдем
параметры линейного уравнения регрессии степенной функции:

Перейдем к
исходным переменным х и у, выполнив потенцирование данного
уравнения:
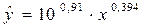
Использовав
функцию СТЕПЕНЬ Мастера функций Excel, получим уравнение
степенной модели регрессии:
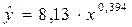
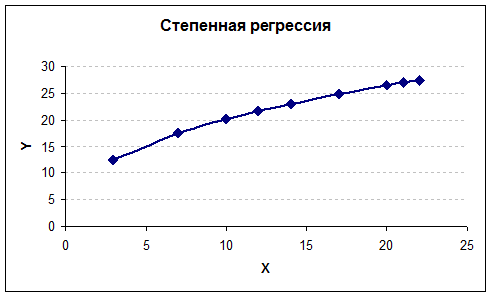
Найдем теоретические
значения y, подставив имеющиеся
значения х в полученное уравнение
регрессии. По этим данным построим график степенной модели регрессии.
в) Показательная функция.
Уравнение показательной
кривой: 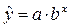
Приведем это
уравнение к линейному виду. Для этого также произведем логарифмирование обеих
частей уравнения (использована функция LOG10 Мастера функций пакета Excel):
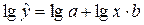 .
.
Введем
обозначения 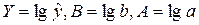 .
.
С учетом этих
обозначений получим линейное уравнение регрессии: Y=A+Bx.
Используя программу Регрессия надстройки Анализ данных пакета Excel, найдем
параметры линейного уравнения регрессии показательной функции:
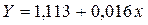 .
.
Перейдем к
исходным переменным x и y, выполнив потенцирование
данного уравнения:
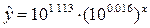
Использовав
функцию СТЕПЕНЬ Мастера функций Excel, получим уравнение
степенной модели регрессии:
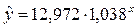
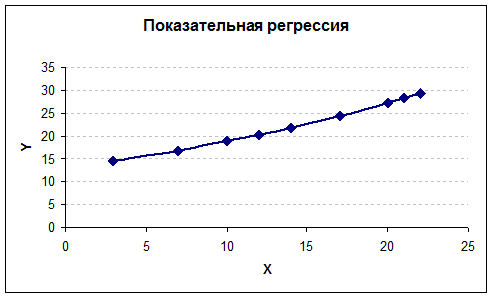
Чтобы найти теоретические значения у, подставим в полученное уравнение имеющиеся
значения х. Построим график
показательной модели регрессии.
9. Для
указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и
средние относительные ошибки аппроксимации.
Сравнить модели по этим характеристикам и сделать вывод.
а) Линейная
модель
Коэффициент
детерминации рассчитывается по формуле (также его можно найти с помощью программы
Регрессия надстройки Анализ данных пакета Excel):
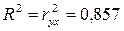
Это означает,
что все изменения в объеме выпуска продукции обусловлены в среднем на 85,7% изменениями объема капиталовложений и на 14,3%
- вариациями неучтенных в модели факторов.
Коэффициент
эластичности для линейной функции рассчитывается по формуле:
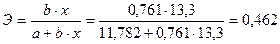
Значит, если
увеличить объем капиталовложений на 1%, то объем выпуска продукции увеличится в
среднем на 462 тыс. руб.
Средняя
относительная ошибка аппроксимации для линейной модели была найдена выше (см.
пункт 5)
б)
Гиперболическая функция
Коэффициент
детерминации рассчитывается по формуле (также его можно найти с помощью программы
Регрессия надстройки Анализ данных пакета Excel):

Это
означает, что все изменения в объеме выпуска продукции обусловлены в среднем на
67,2% изменениями объема
капиталовложений и на 32,8% - вариациями неучтенных в модели факторов.
Коэффициент
эластичности для гиперболы рассчитывается по формуле:
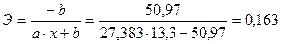
Значит, если
увеличить объем капиталовложений на 1%, то объем выпуска продукции увеличится в
среднем на 163 тыс. руб.
Средняя
относительная ошибка аппроксимации определяется по формуле:

Произведем
расчеты с помощью программы Excel. Чтобы найти 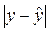 воспользуемся функцией ABS Мастера
функций Excel. Тогда:
воспользуемся функцией ABS Мастера
функций Excel. Тогда:
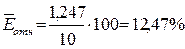
Это означает,
что в среднем расчетные значения 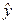 для гиперболической
модели отличаются от фактических значений на 12,47%.
для гиперболической
модели отличаются от фактических значений на 12,47%.
Так как 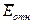 =12,47%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
=12,47%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
в) Степенная
функция
Коэффициент
детерминации рассчитывается по формуле (также его можно найти с помощью программы
Регрессия надстройки Анализ данных пакета Excel):
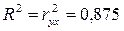
Это означает, что все изменения в объеме выпуска
продукции обусловлены в среднем на 87,5%
изменениями объема капиталовложений и на 12,5% - вариациями
неучтенных в модели факторов.
Коэффициент
эластичности для степенной функции рассчитывается по формуле:
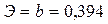
Значит, если
увеличить объем капиталовложений на 1%, то объем выпуска продукции увеличится в
среднем на 394 тыс. руб.
Средняя
относительная ошибка аппроксимации определяется по формуле:

Произведем
расчеты с помощью программы Excel. Чтобы найти 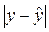 воспользуемся функцией ABS Мастера
функций Excel. Тогда:
воспользуемся функцией ABS Мастера
функций Excel. Тогда:
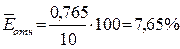 .
.
Это означает,
что в среднем расчетные значения 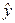 для гиперболической
модели отличаются от фактических значений на 7,65%.
для гиперболической
модели отличаются от фактических значений на 7,65%.
Так как 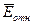 =7,65%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
=7,65%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
г) Показательная функция
Коэффициент
детерминации рассчитывается по формуле (также его можно найти с помощью программы
Регрессия надстройки Анализ данных пакета Excel):
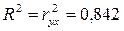
Это
означает, что все изменения в объеме выпуска продукции обусловлены в среднем на
84,2% изменениями объема
капиталовложений и на 15,8% - вариациями неучтенных в модели факторов.
Коэффициент
эластичности для показательной функции рассчитывается по формуле:
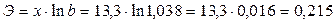
Значит, если
увеличить объем капиталовложений на 1%, то объем выпуска продукции увеличится в
среднем на 215 тыс. руб.
Средняя
относительная ошибка аппроксимации определяется по формуле:
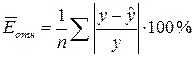
Произведем
расчеты с помощью программы Excel. Чтобы найти 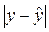 воспользуемся функцией ABS Мастера
функций Excel. Тогда:
воспользуемся функцией ABS Мастера
функций Excel. Тогда:
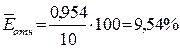 .
.
Это означает,
что в среднем расчетные значения 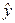 для гиперболической
модели отличаются от фактических значений на 9,54%.
для гиперболической
модели отличаются от фактических значений на 9,54%.
Так как 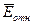 =9,54%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
=9,54%, то
ошибка считается приемлемой, что говорит о хорошем уровне точности модели.
Для сравнения
моделей построим сводную таблицу результатов.
|
Параметры
Модель
|
Коэффициент детерминации R2
|
Коэффициент эластичности Э
|
Средняя относительная ошибка 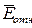 , % , %
|
|
Линейная
|
0,857
|
0,462
|
8,4
|
|
Гиперболическая
|
0,672
|
0,163
|
12,47
|
|
Степенная
|
0,875
|
0,394
|
7,65
|
|
Показательная
|
0,842
|
0,215
|
9,54
|
Сравнивая эти
четыре модели можно сделать вывод, что степенная наилучшим образом подходит для
построения прогноза, т.к. она имеет наилучшие значения коэффициента
детерминации и средней относительной ошибки аппроксимации (т.е. 2-х параметров
из 3-х).