4

4. Докажите, что композиция гомотетий и параллельного переноса является гомотетией с тем же коэффициентом. Является ли гомотетией композиция параллельного переноса и гомотетии.

Решение:

Для решения задачи воспользуемся теоремой о трех центрах подобия:

Теорема о трех центрах подобия. Композицией двух гомотетий является гомотетия или параллельный перенос:

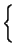
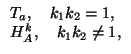
H_A2^k₂oH_A1^k₁ = $\displaystyle \left\{\vphantom{ \begin{array}l T_a,\quad k_1k_2=1,\\ H_A^k,\quad k_1k_2\ne 1, \end{array} }\right.$ $\displaystyle \begin{array}l T_a,\quad k_1k_2=1,\\ H_A^k,\quad k_1k_2\ne 1, \end{array}$

причем в первом случае вектор a параллелен прямой A₁A₂, а во втором случае центр результирующей гомотетии A лежит на прямой A₁A₂ и k = k₁^.k₂. Здесь H_A^k обозначает гомотетию с центром в A с коэффициентом k.

Применим эту теорему к нашей задаче:

Композиция гомотетий

H_A1^k₁ :     w = k₁(z - A₁) + A₁;        H_A2^k₂ :     w = k₂(z - A₂) + A₂

имеет вид

w = k₁^.k₂^.z + k₂(1 - k₁)A₁ + (1 - k₂)A₂.

Если k₁^.k₂ = 1, то получаем параллельный перенос. Если же k₁^.k₂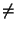 $\ne$ 1, то это гомотетия с коэффициентом k₁^.k₂, центр A которой находится из уравнения

k₁^.k₂^.z + k₂(1 - k₁)A₁ + (1 - k₂)A₂ = k₁^.k₂(z - A) + A.

Если же имеем гомотетии с одинаковыми коэффициентами подобия, то принципиально ничего не меняется, так что композиция гомотетий и параллельного переноса является гомотетией с тем же коэффициентом. При этом является гомотетией композиция параллельного переноса и гомотетии.

5. а) Доказать линейность оператора.

    б) Найти его матрицу в указанном базисе.

    в) Найти образ, ядро и дефект линейного оператора.

№53 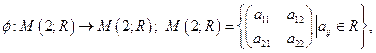 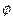  – умножение матриц слева на матрицу 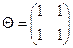. Базис: , , , .

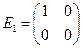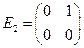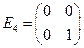Решение:

а) Для доказательства линейности оператора 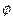необходимо доказать два его свойства, а именно: 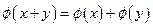и , где .

По свойствам операций с матрицами:

;

.

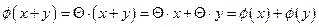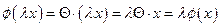Таким образом, доказали линейность оператора.

б) Найдем матрицу оператора в указанном базисе:

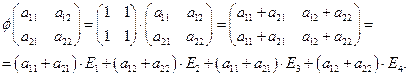
Значит, матрица оператора в указанном базисе .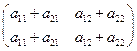

3) Найдем образ, ядро и дефект линейного оператора.

Поскольку 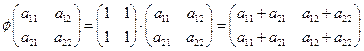, то образом линейного оператора являются матрицы .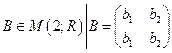

Ядром линейного оператора называется множество элементов из его области определения , образом которых является нулевой элемент. Ядро оператора обозначают

: .

Исходя из этого определения найдем ядро оператора 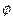из следующего матричного уравнения:

.

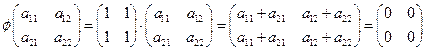Отсюда 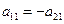; . Значит,

.

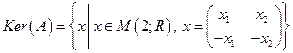Размерность ядра линейного оператора называется дефектом оператора. Поскольку 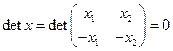, то дефект оператора 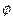равен 1.

6. Матрица оператора 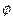в базисе 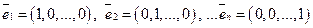равна А. Найти его матрицу в базисе , , …, .

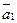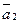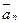№63         .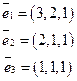

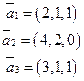
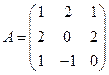Решение:

Найдем матрицу перехода между двумя базисами:

.

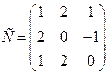Найдем матрицу, обратную C:

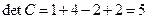. Найдя алгебраические дополнения к каждому элементу матрица А, найдем обратную матрицу:

.

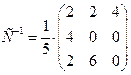Тогда искомая матрица:

.

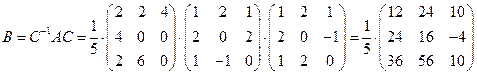7. Можно ли привести матрицу линейного оператора к диагональному виду путем перехода к новому базису? Найти базис и соответствующую ему диагональную матрицу.

№73 .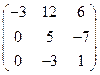

Решение:

Такое возможно. Для приведенной в условии задачи матрицы таким базисом может быть следующая система матриц:

, , .

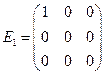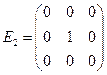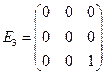Соответствующая диагональная матрица:

.
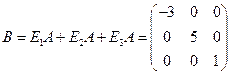