Содержание
1.
Теоретическая часть: Представление информации в ЭВМ... 3
1.1.
Арифметические основы работы на ЭВМ.. 3
1.2.
Системы счисления. 5
1.3.
Перевод чисел из одной категории в другую.. 9
1.4.
Понятие файла (имя, расширение) 11
1.5.
Понятие каталога (папки) 11
2.
Практическая часть. 12
4.
Список литературы.. 17
1. Теоретическая часть: Представление информации в
ЭВМ
1.1. Арифметические основы работы на ЭВМ
Все
современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и
сотни машинных операций. Однако выполнение любой операции основано на
использовании простейших микроопераций типа сложения и сдвиг. Это позволяет
иметь единое арифметико-логическое устройство для выполнения любых операций,
связанных с обработкой информации. Правила сложения двоичных цифр двух чисел А
и В представлены в табл.1.[1]
Здесь
показаны правила сложения двоичных цифр ai, bi одноименных разрядов с учетом
возможных переносов из предыдущего разряда pi-1.
Подобные
таблицы можно было бы построить для любой другой арифметической и логической
операции (вычитание, умножение и т.д.), но именно данные этой таблицы положены
в основу выполнения любой операции ЭВМ. Под знак чисел отводится специальный
знаковый разряд. Знак ⌠+ кодируется двоичным нулем, а знак ⌠- -
единицей. Действия над прямыми кодами двоичных чисел при выполнении операций
создают большие трудности, связанные с необходимостью учета значений знаковых
разрядов:
Таблица 1
Правила сложения двоичных цифр
|
Значения
двоичных
чисел А и В
|
Разряд
Суммы
Si
|
Перенос в
следующий разряд
Рi
|
|
аi
|
bi
|
Pi-1
|
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
1
0
1
0
0
1
|
0
0
0
1
0
1
1
1
|
-
во-первых, следует отдельно обрабатывать
значащие разряды чисел и разряды знака;
-
во-вторых, значение разряда знака влияет на
алгоритм выполнения операции (сложение может заменяться вычитанием и наоборот).
Во всех ЭВМ
без исключения все операции выполняются над числами, представленными
специальными машинными кодами. Их использование позволяет обрабатывать знаковые
разряды чисел так же, как и значащие разряды, а также заменять операцию
вычитания операцией сложения.
Различают
прямой код (П), обратный код (ОК) и дополнительный код (ДК) двоичных чисел.
Прямой код
двоичного числа образуется из абсолютного значения этого числа и кода знака
(нуль или единица) перед его старшим числовым разрядом.
Пример 1.
A10=+10
A2=+1010 [A2]П=0:1010;
B10=-15 B2=-1111 [B2]П=1:1111.
Точечной
вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд
от значащих.
Обратный код
двоичного числа образуется по следующему правилу. Обратный код положительных
чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит
единицу в знаковом разряде числа, а значащие разряды числа заменяются на
инверсные, т.е. нули заменяются единицами, а единицы - нулями.[2]
Пример 2.
A10=+5
A2=+101 [A2]П=[A2]OK=0:101;
B10=-13 B2=-1010 [B2]OK=1:0010.
Свое название
обратный код чисел получил потому, что коды цифр отрицательного числа заменены
на инверсные. Укажем наиболее важные свойства обратного кода чисел:
∙
сложение положительного числа С с его отрицательным значением в обратном коде
дает так называемую машинную единицу МЕок= 1: 111... 11, состоящую из единиц в
знаковом и значащих разрядах числа;
∙ нуль
в обратном коде имеет двоякое значение. Он может быть положительным - 0: 00...0
и отрицательным числом - 1; 11... 11. Значение отрицательного нуля совпадает с
МЕок. Двойственное представление нуля явилось причиной того, что в современных
ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код положительных чисел совпадает с их прямым кодом.
Дополнительный код отрицательного числа представляет собой результат
суммирования обратного кода числа с единицей младшего разряда (2° - для
целых чисел, 2-k - для дробных).
Укажем
основные свойства дополнительного кода: сложение дополнительных кодов
положительного числа С с его отрицательным значением дает так называемую машинную
единицу дополнительного кода:
МЕДК=МЕОК+20=10:
00┘00,
т.е. число 10
(два) в знаковых разрядах числа;
дополнительный
код получил такое свое название потому, что представление отрицательных чисел
является дополнением прямого кода чисел до машинной единицы МЕдк.
Модифицированные
обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных
и дополнительных кодов удвоением значений знаковых разрядов. Знак ⌠+ в
этих кодах кодируется двумя нулевыми знаковыми разрядами, а ⌠- - двумя
единичными разрядами.
Целью
введения модифицированных кодов являются фиксация и обнаружение случаев получения
неправильного результата, когда значение результата превышает максимально
возможный результат в отведенной разрядной сетке машины. В этом случае перенос
из значащего разряда может исказить значение младшего знакового разряда. Значение
знаковых разрядов ⌠01 свидетельствует о положительном переполнении
разрядной сетки, а ⌠10 - об отрицательном переполнении. В настоящее время
практически во всех моделях ЭВМ роль удвоенных разрядов для фиксации
переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового
разряда.
1.2. Системы счисления
Система
счисления - это совокупность правил и приемов записи чисел с помощью набора
цифровых знаков. Количество цифр, необходимых для записи числа в системе,
называют основанием системы счисления. Основание системы записывается в справа
числа в нижнем индексе:
; 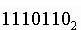 ;
; 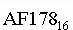
и т. д.
Различают два
типа систем счисления:
-
позиционные, когда значение каждой цифры числа
определяется ее позицией в записи числа;
-
непозиционные, когда значение цифры в числе не
зависит от ее места в записи числа.
Примером
непозиционной системы счисления является римская: числа IX, IV, XV и т.д.
Примером позиционной системы счисления является десятичная система, используемая
повседневно.
Любое целое
число в позиционной системе можно записать в форме многочлена:
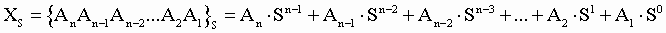
где S -
основание системы счисления;
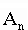 - цифры
числа, записанного в данной системе счисления;
- цифры
числа, записанного в данной системе счисления;
n -
количество разрядов числа.
Пример. Число
629310 запишется в форме многочлена следующим образом:
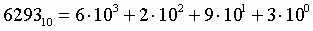
Римская
система счисления является непозиционной системой. В ней для записи чисел
используются буквы латинского алфавита. При этом буква I всегда означает единицу,
буква - V пять, X - десять, L - пятьдесят, C - сто, D - пятьсот, M - тысячу и
т.д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской
системе счисления значением числа является алгебраическая сумма цифр, в него
входящих. При этом цифры в записи числа следуют, как правило, в порядке
убывания их значений, и не разрешается записывать рядом более трех одинаковых
цифр. В том случае, когда за цифрой с большим значением следует цифра с
меньшим, ее вклад в значение числа в целом является отрицательным. Типичные
примеры, иллюстрирующие общие правила записи чисел в римской система счисления,
приведены в таблице.
Таблица 2
Запись чисел в римской системе счисления
|
1
|
2
|
3
|
4
|
5
|
|
I
|
II
|
III
|
IV
|
V
|
|
6
|
7
|
8
|
9
|
10
|
|
VI
|
VII
|
VIII
|
IX
|
X
|
|
11
|
13
|
18
|
19
|
22
|
|
XI
|
XIII
|
XVIII
|
XIX
|
XXII
|
|
34
|
39
|
40
|
60
|
99
|
|
XXXIV
|
XXXIX
|
XL
|
LX
|
XCIX
|
|
200
|
438
|
649
|
999
|
1207
|
|
CC
|
CDXXXVIII
|
DCXLIX
|
CMXCIX
|
MCCVII
|
|
2045
|
3555
|
3678
|
3900
|
3999
|
|
MMXLV
|
MMMDLV
|
MMMDCLXXVIII
|
MMMCM
|
MMMCMXCIX
|
Недостатком римской системы является отсутствие формальных правил записи чисел
и, соответственно, арифметических действий с многозначными числами. По причине
неудобства и большой сложности в настоящее время римская система счисления
используется там, где это действительно удобно: в литературе (нумерация глав),
в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных
целях на циферблате часов и в ряде других случаев.
Десятичня
система счисления – в настоящее время наиболее известная и используемая.
Изобретение десятичной системы счисления относится к главным достижениям человеческой
мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная
техника. Причина, по которой десятичная система счисления стала общепринятой,
вовсе не математическая. Люди привыкли считать в десятичной системе счисления,
потому что у них по 10 пальцев на руках.
Древнее изображение
десятичных цифр (рис) не случайно: каждая цифра обозначает число по количеству
углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д.
Написание десятичных цифр претерпело существенные изменения. Форма, которой мы
пользуемся, установилась в XVI веке.

Десятичная
система впервые появилась в Индии примерно в VI веке новой эры. Индийская
нумерация использовала девять числовых символов и нуль для обозначения пустой
позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в
обратном порядке - наиболее значимая цифра ставилась справа. Но вскоре стало
правилом располагать такую цифру с левой стороны. Особое значение придавалось
нулевому символу, который вводился для позиционной системы обозначений.
Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе
индусские приёмы десятичной арифметики получили распространение в начале ХIII
в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи).
Европейцы заимствовали индийскую систему счисления у арабов, назвав ее
арабской. Это исторически неправильное название удерживается и поныне.
Десятичная
система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы
“+” и “–” для обозначения знака числа и запятую или точку для разделения целой
и дробной частей числа.
В
вычислительных машинах используется двоичная система счисления, её основание -
число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1.
Вопреки распространенному заблуждению, двоичная система счисления была
придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго
до появления компьютеров, еще в ХVII - ХIХ веках. Первое опубликованное
обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану
Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла
статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703
г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления.
Лейбниц не рекомендовал использовать эту систему для практических вычислений,
но подчёркивал её важность для теоретических исследований. Со временем двоичная
система счисления становится хорошо известной и получает развитие.
Выбор
двоичной системы для применения в вычислительной технике объясняется тем, что
электронные элементы - триггеры, из которых состоят микросхемы ЭВМ, могут
находиться только в двух рабочих состояниях.
С помощью
двоичной системы кодирования можно зафиксировать любые данные и знания. Это
легко понять, если вспомнить принцип кодирования и передачи информации с
помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки -
точки и тире, может передать практически любой текст.
Двоичная
система удобна для компьютера, но неудобна для человека: числа получаются
длинными и их трудно записывать и запоминать. Конечно, можно перевести число в
десятичную систему и записывать в таком виде, а потом, когда понадобится
перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы
счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи
чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной
первые 10 цифр общие, а дальше используют заглавные латинские буквы.
Шестнадцатеричная цифра A соответствует десятеричному числу 10,
шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем
объясняется тем, что переход к записи числа в любой из этих систем от его
двоичной записи очень прост. Ниже приведена таблица соответствия чисел,
записанных в разных системах.
Таблица 3
Соответствие чисел, записанных в различных системах счисления
|
Десятичная
|
Двоичная
|
Восьмеричная
|
Шестнадцатеричная
|
|
1
|
001
|
1
|
1
|
|
2
|
010
|
2
|
2
|
|
3
|
011
|
3
|
3
|
|
4
|
100
|
4
|
4
|
|
5
|
101
|
5
|
5
|
|
6
|
110
|
6
|
6
|
|
7
|
111
|
7
|
7
|
|
8
|
1000
|
10
|
8
|
|
9
|
1001
|
11
|
9
|
|
10
|
1010
|
12
|
A
|
|
11
|
1011
|
13
|
B
|
|
12
|
1100
|
14
|
C
|
|
13
|
1101
|
15
|
D
|
|
14
|
1110
|
16
|
E
|
|
15
|
1111
|
17
|
F
|
|
16
|
10000
|
20
|
10
|
1.3. Перевод чисел из одной категории в другую
Перевод чисел
из одной системы счисления в другую составляет важную часть машинной
арифметики. Рассмотрим основные правила перевода.[3]
1. Для
перевода двоичного числа в десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр числа и соответствующей степени
числа 2, и вычислить по правилам десятичной арифметики:
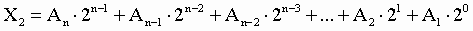
При переводе
удобно пользоваться таблицей степеней двойки:
Таблица 4
Степени числа 2
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
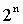
|
1
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
256
|
512
|
1024
|
2. Для
перевода восьмеричного числа в десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр числа и соответствующей степени
числа 8, и вычислить по правилам десятичной арифметики:
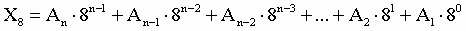
При переводе
удобно пользоваться таблицей степеней восьмерки:
Таблица 5
Степени числа 8
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
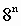
|
1
|
8
|
64
|
512
|
4096
|
32768
|
262144
|
3. Для
перевода шестнадцатеричного числа в десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр числа и соответствующей степени
числа 16, и вычислить по правилам десятичной арифметики:
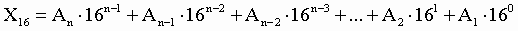
При переводе
удобно пользоваться таблицей степеней числа 16:
Таблица 6
Степени числа 16
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
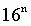
|
1
|
16
|
256
|
4096
|
65536
|
1048576
|
16777216
|
4. Для
перевода десятичного числа в двоичную систему его необходимо последовательно делить
на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в
двоичной системе записывается как последовательность последнего результата
деления и остатков от деления в обратном порядке.
5. Для
перевода десятичного числа в восьмеричную систему его необходимо
последовательно делить на 8 до тех пор, пока не останется остаток, меньший или
равный 7. Число в восьмеричной системе записывается как последовательность цифр
последнего результата деления и остатков от деления в обратном порядке.
6. Для
перевода десятичного числа в шестнадцатеричную систему его необходимо
последовательно делить на 16 до тех пор, пока не останется остаток, меньший или
равный 15. Число в шестнадцатеричной системе записывается как
последовательность цифр последнего результата деления и остатков от деления в
обратном порядке.
7. Чтобы
перевести число из двоичной системы в восьмеричную, его нужно разбить на триады
(тройки цифр), начиная с младшего разряда, в случае необходимости дополнив
старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной
цифрой (табл. 3).
8. Чтобы
перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на
тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости
дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей
восьмеричной цифрой (табл. 3).
9. Для
перевода восьмеричного числа в двоичное необходимо каждую цифру заменить
эквивалентной ей двоичной триадой.
10. Для
перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить
эквивалентной ей двоичной тетрадой.
11. При
переходе из восьмеричной системы счисления в шестнадцатеричную и обратно,
необходим промежуточный перевод чисел в двоичную систему.
1.4. Понятие файла
(имя, расширение)
Файл -
организованный набор данных с определенным именем, хранится на диске или другом
магнитном носителе.[4]
Имя файла -
состоит из двух частей: имя. расширение.
Стандартные
расширения характеризуют тип файла (например, программные - exe, текстовые -
txt, рисунки - bmp, gif, wmf, jpg, jpeg).
1.5. Понятие каталога
(папки)
|
Папка - это
специальный объект для упорядоченного хранения файлов. Папки позволяют организовать
удобное размещение файлов
В среде
Windows папки и файлы представлены особыми значками с подписями. Используя
основные приемы работы с мышкой, можно довольно успешно выполнять основные
операции с файлами и папками. Но в некоторых случаях удобнее пользоваться
специальными приложениями или командами контекстного меню.[5]
|
Для
создания файла или папки достаточно:
-
раскрыть диск и при необходимости папку, в
которой будет создан новый объект;
-
в меню Файл выбрать команду Создать;
-
в появившемся списке выбрать нужный объект;
-
в строке рядом со значком объекта набрать его
имя.
Для
удаления файлов или папок выполняются следующие действия:
-
o выбрать нужные объекты;
-
o нажать клавишу Delete.
Для
перемещения или копирования объектов выполняются очень похожие действия:
-
o выбрать нужные объекты;
-
o для перемещения выбрать в меню Правка
команду Вырезать,
-
для копирования выбрать в меню Правка команду
Копировать;
-
o открыть диск и/или папку для перемещаемого
или копируемого объекта (объектов);
-
o выбрать в меню Правка команду Вставить.
-
|
2. Практическая часть
Дана следующая таблица.
|
ФИО
|
Разряд
|
Часовая тарифная
ставка
|
Отработано,
ч.
|
Начислено
|
Сумма всех
начислений, руб.
|
|
Всего
|
В том
числе сверхсуточно
|
Повременно
|
Сверхсуточно
|
|
FIO
|
R
|
TS
|
OV
|
OS
|
NP
|
NS
|
SUM
|
|
Ким Л.Н.
|
5
|
27,3
|
188
|
36
|
|
|
|
|
Аппалонова
А.В.
|
6
|
25,4
|
170
|
13
|
|
|
|
|
Кравченко
М.В.
|
4
|
30,1
|
188
|
15
|
|
|
|
|
Соколов
В.Н.
|
6
|
34,0
|
156
|
25
|
|
|
|
|
Коновалов
С.В.
|
7
|
40,8
|
176
|
26
|
|
|
|
|
Рогачев
Н.А.
|
2
|
32,7
|
156
|
5
|
|
|
|
|
Теханова
В.С.
|
8
|
34,8
|
163
|
7
|
|
|
|
|
Хлебникова
З.А.
|
4
|
29,4
|
168
|
19
|
|
|
|
|
Белин Ю.С.
|
6
|
31,8
|
163
|
2
|
|
|
|
|
Федосов
А.К.
|
7
|
30,0
|
187
|
28
|
|
|
|
|
Итого
|
|
|
|
|
|
|
|
Необходимо создать ведомость о начислении
заработной платы рабочим предприятия, которая должна содержать для каждого
рабочего строку, включающую следующие данные: FIO, R, TS, OV, OS, NP, NS, SUM. Доплата за час, отработанный сверхурочно составляет 50% от
часовой тарифной ставки.
Выходной документ должен содержать:
1. расчет данных в графах 6, 7, 8 в каждой
строке таблицы по формулам:
NP = TS*OV;
NS = 0.5*TS*OS
SUM = NP + NS
2. Итоговые данные по предприятию в графах
6, 7, 8.
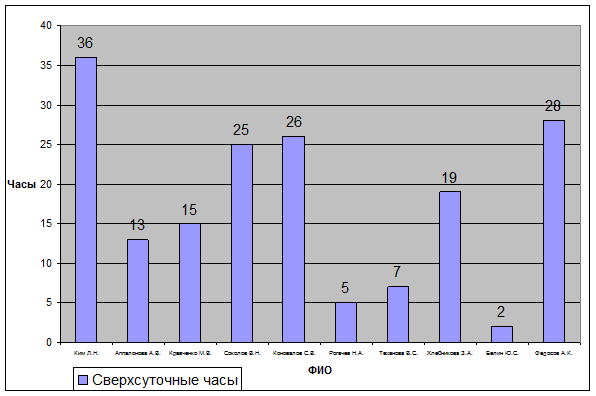
Построить гистограмму часов, отработанных
сверхурочно каждым рабочим предприятия.
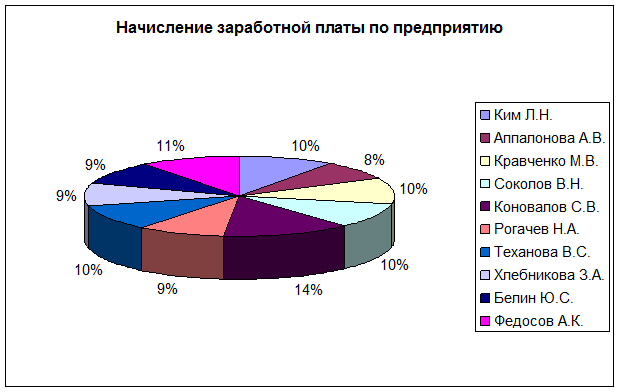
Построить круговую диаграмму начисления
заработной платы по всему предприятию.
Ответить на вопросы:
1. У кого из рабочих самая высокая и самая
низкая заработная плата;
2. Какова средняя сумма всех начислений по
предприятию;
3. С помощью фильтра получить информацию о
рабочих, чья сумма начисления является ниже средней по предприятию;
4. С помощью фильтра получить информацию о
рабочих кто отработал сверхурочно от 25 до 35 часов.
Решение:
Рассчитаем недостающие показатели
в таблице
|
ФИО
|
Разряд
|
Часовая
тарифная ставка
|
Отработано,
ч.
|
Начислено
|
Сумма всех
начислений, руб.
|
|
Всего
|
В том числе
сверхсуточно
|
Повременно
|
Сверхсуточно
|
|
FIO
|
R
|
TS
|
OV
|
OS
|
NP
|
NS
|
SUM
|
|
Ким Л.Н.
|
5
|
27,3
|
188
|
36
|
5132,4
|
491,4
|
5623,8
|
|
Аппалонова
А.В.
|
6
|
25,4
|
170
|
13
|
4318,0
|
165,1
|
4483,1
|
|
Кравченко
М.В.
|
4
|
30,1
|
188
|
15
|
5658,8
|
225,75
|
5884,6
|
|
Соколов
В.Н.
|
6
|
34,0
|
156
|
25
|
5304,0
|
425
|
5729,0
|
|
Коновалов
С.В.
|
7
|
40,8
|
176
|
26
|
7180,8
|
530,4
|
7711,2
|
|
Рогачев
Н.А.
|
2
|
32,7
|
156
|
5
|
5101,2
|
81,75
|
5183,0
|
|
Теханова
В.С.
|
8
|
34,8
|
163
|
7
|
5672,4
|
121,8
|
5794,2
|
|
Хлебникова
З.А.
|
4
|
29,4
|
168
|
19
|
4939,2
|
279,3
|
5218,5
|
|
Белин Ю.С.
|
6
|
31,8
|
163
|
2
|
5183,4
|
31,8
|
5215,2
|
|
Федосов
А.К.
|
7
|
30,0
|
187
|
28
|
5610,0
|
420
|
6030,0
|
|
Итого
|
|
|
|
|
54100,2
|
2772,3
|
56872,5
|
В формульном виде она будет выглядеть следующим образом:
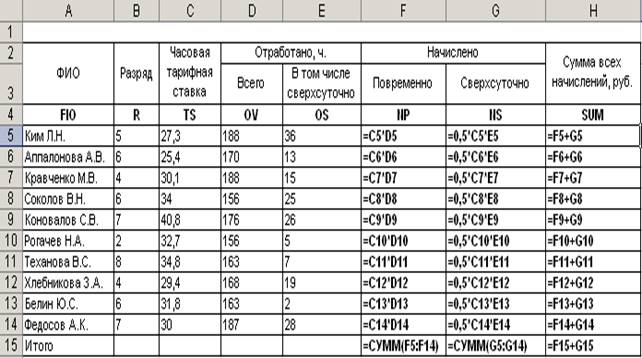
Построим
гистограмму часов, отработанных сверхурочно каждым рабочим предприятия.
Построим
круговую диаграмму начисления заработной платы по всему предприятию.
Ответы на
вопросы:
1. У кого из
рабочих самая высокая и самая низкая часовая тарифная ставка.
Воспользовавшись
функцией МАКС получим 40,8 самая высокая тарифная ставка у Коновалова
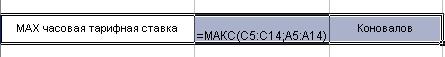
Воспользовавшись
функцией МИН получим 25,4 самая низкая тарифная ставка у Аппалоновой А.В.

2. Какова
средняя сумма всех начислений по предприятию
Воспользовавшись
функцией СРЗНАЧ получили 5687,3 руб.

3. С помощью
фильтра получить информацию о рабочих, чья сумма начисления является ниже
средней по предприятию.
Воспользуемся
автофильтром
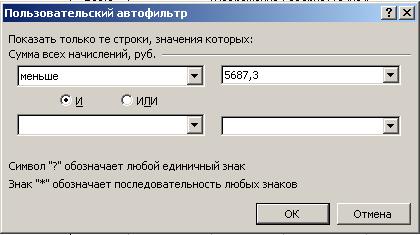
После нажатия ОК получим:

Таким
образом, у Кима, Аппалоновой, Рогачева, Хлебниковой и Белина сумма начисления
является ниже средней по предприятию.
4. С помощью
фильтра получить информацию о рабочих кто отработал сверхурочно от 25 до 35 часов.
Воспользуемся
автофильтром
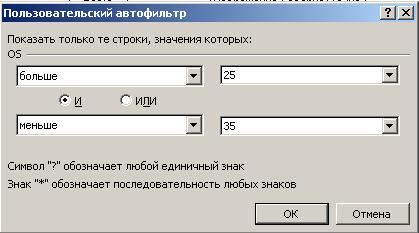
После нажатия ОК получим:

Таким
образом, Коновалов и Федосов отработали сверхурочно от 25 до 35 часов.
4. Список литературы
1.
Багриновский К.А., Хрусталев Е.Ю. Новые информационные
технологии. - М.: “ЭКО”. 2004.
2.
Белинов С.В., Зайцев А.А. Современные информационные
технологии. – М.: Инфра-М, 2003.
3.
Иванченко Н.М. Компьютерные методы обработки
информации: УМК. – СПб.: Питер, 2004.
4.
Каpатыгин С.Н.
Информационные технологии в коммерческой деятельности. - М.: ABF, 2004.
5.
Майоров С.И. Информационные технологии. - М.: Информатика, 2003.
6.
Макарова Н. В., Матвеева Л. А., Бройдо В. Л. Информатика:
Учебник. - М.: Финансы и статистика,
2004.
7.
Шафрин Ю. А. Основы компьютерной технологии. - М.:
АБФ, 2005.
[1] Белинов
С.В., Зайцев А.А. Современные информационные технологии. – М.: Инфра-М, 2003. –
с. 59.
[2] Багриновский
К.А., Хрусталев Е.Ю. Новые информационные технологии. - М.: “ЭКО”. 2004. – с.
69.
[3] Иванченко
Н.М. Компьютерные методы обработки информации: УМК. – СПб.: Питер, 2004. – с.
137.
[4] Макарова
Н. В., Матвеева Л. А., Бройдо В. Л. Информатика: Учебник. - М.: Финансы и статистика, 2004. – с. 175.
[5] Майоров
С.И. Информационные технологии. - М.:
Информатика, 2003. – с. 189.