Вопрос
2.
СВОЙСТВА
ВЕРОЯТНОСТЕЙ, ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
(ВОПРОСЫ)
1. (2)
Вероятности
событий A и B равны соответственно 0,5 и 0,6. Каким из следующих
свойств обладают эти события?
2. Совместны
2. (3)
Какими из
перечисленных свойств не могут обладать события A и B, если их вероятности равны соответственно
0,6 и 0,3.
Ответы: 1. Образуют полную группу событий
3. Противоположны
3. (2)
Вероятность суммы двух совместных
событий A и B равна:
2. 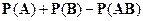
4. (2)
Вероятность произведения двух зависимых
событий A и B равна:
2. 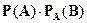
5. (2)
Вероятность
произведения двух несовместных событий A и B равна:
2. 0
6. (2)
Пусть A – случайное событие, найти 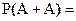
Ответы: 1. 
7. (2)
Пусть A – случайное событие, найти 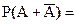
4. 1
8. (2)
Пусть A – случайное событие, найти 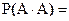
Ответы: 1. 
9. (2)
Пусть A – случайное событие, найти 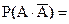
3. 0
4. 1
10. (2)
Если наступление
события B влечет за собой
наступление события A, то
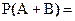
2. 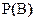
11. (2)
Если наступление
события B влечет за собой
наступление события A, то
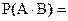
Ответы: 1. 
12. (2)
Если наступление
события B влечет за собой
наступление события A, то
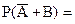
4. 1
13. (2)
Если наступление
события B влечет за собой
наступление события A, то
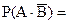
3. 0
14. (4)
Вероятности
событий A и B равны
соответственно 0,3 и 0,4. Чему равна вероятность их суммы, если вероятность их
произведения 0,2?
Правильный
ответ: 0,5.
15. (4)
Вероятности
событий A и B равны
соответственно 0,3 и 0,4. Чему равна вероятность их суммы, если вероятность их
произведения 0,1?
Правильный
ответ: 0,6.
16. (4)
Вероятности
событий A и B равны
соответственно 0,3 и 0,4. Чему равна вероятность их произведения, если
вероятность их суммы 0,5?
Правильный
ответ: 0,2.
17. (4)
Вероятности событий A и B равны
соответственно 0,3 и 0,2. Чему равна вероятность их произведения, если
вероятность их суммы 0,5?
Правильный
ответ: 0.
18. (4)
Вероятности событий A и B равны соответственно
0,3 и 0,4. Чему равна вероятность их произведения, если вероятность их суммы
0,4?
Правильный
ответ: 0,3.
19. (4)
Студент Иванов
посещает лекции по математике с вероятностью 0,8, студент Петров с вероятностью
0,7, а вместе они встречаются на шести лекциях из десяти. Какова вероятность
того, что хотя бы один из них присутствует на лекции?
Правильный
ответ: 0,9.
20. (4)
Студент Иванов
посещает лекции по математике с вероятностью 0,8, студент Петров с вероятностью
0,7, хотя бы один из них присутствует на каждой лекции. Какова вероятность
того, что они встретились на лекции?
Правильный
ответ: 0,5.
21. (4)
В группе учатся двое юношей. Каждый из
них пропускает в среднем две лекции из десяти, при этом на каждой лекции
присутствует хотя бы один из них. Какова вероятность того, что на лекции
присутствуют оба юноши?
Правильный
ответ: 0,6.
22. (4)
В группе учатся двое юношей. Каждый из
них пропускает в среднем две лекции из десяти. Какова вероятность того, что на
лекции присутствует хотя бы один юноша, если они встречаются на лекциях с
вероятностью 0,7?
Правильный
ответ: 0,9.