Планируется деятельность двух отраслей производства I и II сроком на 3 года (N=3). Заданы функции дохода 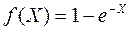, 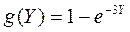и траты , 

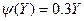
требуется распределить имеющиеся средства в размере K0=2 между отраслями исходя из условия максимума дохода.

В нашем случае система - две отрасли с вложенными в них средствами. Она характеризуется двумя параметрами X и Y, выражающими количество средств в I и II отраслях соответственно. Шаг процесса равен 1 году. В процессе управления величины X и Y меняются в зависимости от двух причин: - перераспределение средств между отраслями в начале каждого года; - уменьшение средств к концу каждого года.

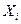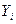Управление на i-ом шаге - количество средств и, вложенных в отрасли I и II на этом шаге. Нужно найти такое оптимальное управление, при котором суммарный доход 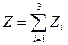будет максимальным.

Состояние системы перед i-ым шагом характеризуется количеством средств Q, сохранившихся после предыдущих i-1 шагов. Управление на i-ом шаге будет состоять в выделении в отрасль I средств в объеме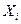,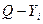. Выигрыш на i-ом шаге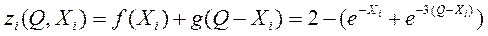. Новое состояние системы перед i+1 шагом .

Основное функциональное уравнение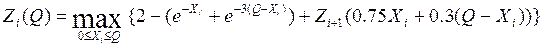

Условным оптимальным управлением будет то, при котором достигается указанный максимум.

Условный оптимальный выигрыш на последнем 3-ем шаге равен

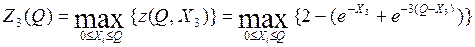
Выражение в скобках равно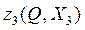 - выигрыш на третьем шаге. Вид этой функции показан на рис.1 при 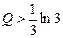и на рис.2 при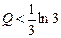. Найдем ее максимум при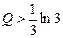

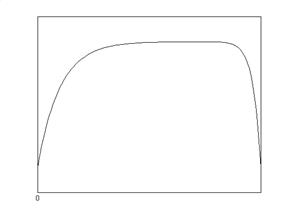
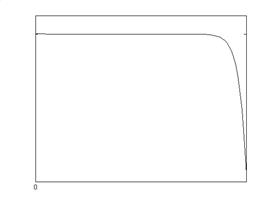
                        Рис. 1                                                  Рис. 2 (x5=0)

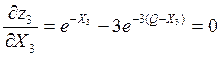 В этом случае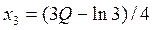

В общем случае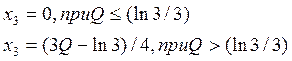

Это означает, что если мы подошли к последнему этапу с запасом средств не превышающим (ln3)/3, то их все нужно вложить во II отрасль. В противном случае в I отрасль нужно вложить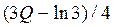, а во II отрасль -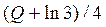. Условный оптимальный выигрыш на последнем шаге будет равен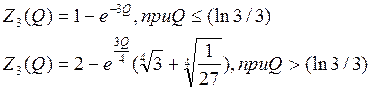

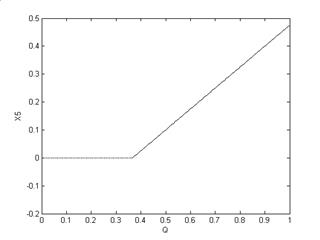
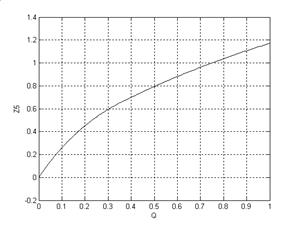
Рис 3. зависимость X5 от Q                                                 Рис 4 зависимость Z5 от Q

Задачу условной оптимизации будем решать численно: 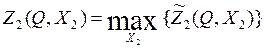, где условный полуоптимальный выигрыш равен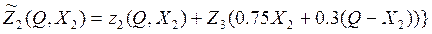

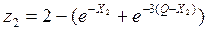- выигрыш на 2-ом шаге. Выясним в каких пределах может находиться Q, т.е. Qmin и Qmax. Значение Qmax можно найти, считая, что на первом шаге все средства будут вложены в первую отрасль, в которой затраты максимальны. Тогда после одного года Qmax=0,75. Величину Qmin можно найти, если на первом шаге все средства вкладывать во вторую отрасль, Qmin=0,3. Возьмем опорные значения Q=0.3, 0.4, …, 0.7 и для каждого из них найдем условное оптимальное управление x2(Q) и условный максимальный доход на двух последних шагах Z2(Q).

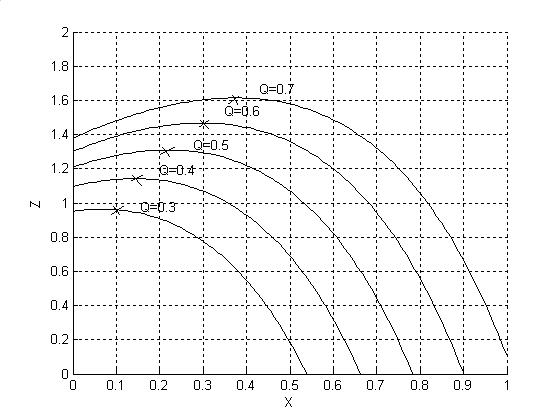
Рис 5.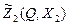

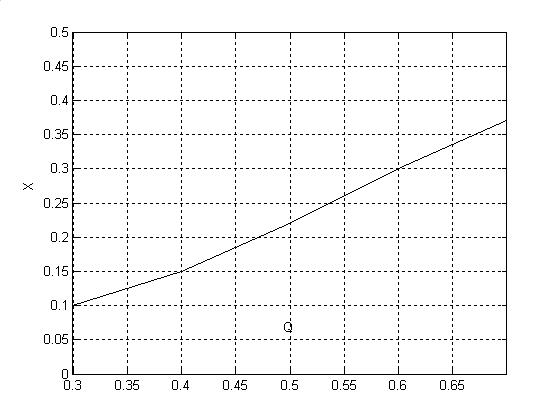
Рис. 6 X2(Q)

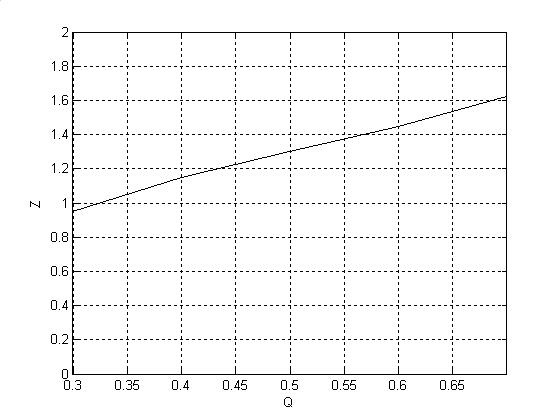
Рис. 7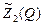

Теперь остается оптимизировать первый шаг. Начальное состояние системы K0=2 и нужно построить зависимость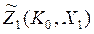 

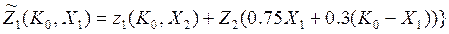
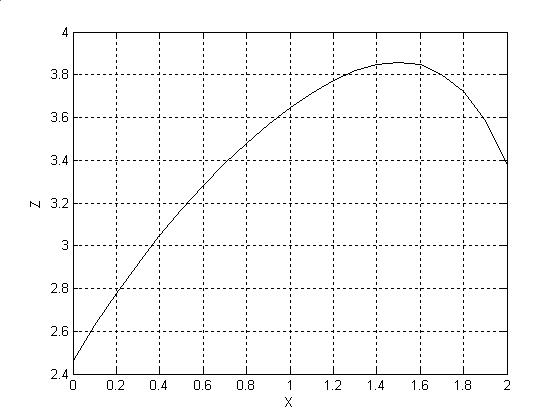
Рис 8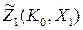

Оптимальное управление на первом шаге x1=1.5 (максимум на графике).

Найдем безусловные оптимальные управления по схеме

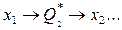
Q2=1.2750;

x2=0.82;

Q3= 0.7515;

x3=0.22;

Окончательные результаты сведены в таблице

Отрасли

1

2

3

I

1,5

0,82

0,22

II

0,5

0,455

0,5315