Введение

Предложена новая запись центрального взаимодействия элементарных частиц, более отвечающая принципу близкодействия зарядов. Показано, что введение раздельных параметров, характеризующих тело как источник электрического поля и объект воздействия внешних полей позволяет рассматривать гравитационное взаимодействие как компоненту электростатического поля, существующую вследствие несовпадения состояний электрической нейтральности тела относительно электронов и протонов. Кроме электростатического и гравитационного полей новая запись предсказывает существование третьей компоненты центрального взаимодействия (смешанной), которая проявляется между заряженным и электрически нейтральным телами.

Во всем диапазоне пространственных масштабов, от размеров атомного ядра до метагалактики, ведущая роль принадлежит центральным взаимодействиям, т. е. электростатическому и гравитационному полям, поэтому от понимания их природы и взаимосвязи зависит успех решения многих теоретических и практических задач. Этим объясняется, почему на протяжении многих десятилетий объединение фундаментальных взаимодействий является одной из важнейших и наиболее обсуждаемых задач теоретической физики.

В тридцатые годы были установлены сложная структура атома и наличие в нем элементарных частиц трех типов: электронов, протонов и нейтронов. C тех пор оставалось незамеченным, как это представляется теперь, что построенная модель атома открывала путь для нового решения проблемы объединения двух центральных полей. Всеобщее увлечение и покоренность идеей отождествления феномена гравитации с кривизной пространства были настолько сильны, что высказывавшиеся в различные годы все новые аргументы против, даже имевшие весьма надежные основания, не могли остановить развития направления. Основания против такого отождествления, создавшего видимость принципиального различия гравитационного и электростатического полей, остаются до настоящего времени. Одно из них состоит в следующем.

Согласно принципу суперпозиции гравитация любого тела складывается из гравитации составляющих его атомов, точнее из входящих в эти атомы элементарных частиц, в основном протонов и нейтронов. Если в первом приближении рассматривать нейтрон как суперпозицию протона и электрона, то в конечном итоге гравитацию следует связывать в основном с протонами. Таким образом, протон оказывается источником двух качественно равноправных и структурно идентичных центральных полей - электростатического и гравитационного, причем само существование гравитационного поля между двумя протонами или двумя электронами весьма условно: практически эффект притяжения обнаруживается только между протоном и электроном или между сложными системами, содержащими и протоны, и электроны, каковыми являются макротела и атомы. Количественно электростатическое взаимодействие двух протонов сильнее расчетного гравитационного взаимодействия атомов водорода в 1036 раз. Ввиду такого количественного соотношения эффектов двух полей современные поиски связи кривизны пространства с пренебрежимо слабым полем гравитации не представляются оправданными и единственно возможными.

В то же время, с момента сформирования основных положений современной модели атома, были созданы необходимые условия для решения задачи объединения гравитационного взаимодействия с электростатическим, вариант такого объединения описан ниже.

Цель работы – раскрыть сущность вопроса связанного с гравитационными и электромагнитными полями и их свойствами.

1. Гравитационное поле и его свойства

Гравитационное поле  - (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел (смотри Всемирного тяготения закон).[1]

Гравитационные поля, согласно альтернативной эфирной физики, выражаются в виде полей с переменным эфирным давлением; их способность создавать тяготение-гравитацию характеризуется градиентом давления. В космическом эфирном пространстве гравитационные поля возникают вокруг планет и звёзд, и вызывается это распадом и аннигиляцией атомов и электронов внутри них.

Основой основ эфирной физики является закон неравномерных деформаций, согласно которому любые движения элементарных эфирных частиц (эфирных шариков) приводят к уменьшению их плотности. Другими словами, находящиеся во взаимном движении эфирные шарики занимают всегда больший объем (за счёт увеличения пустот между ними), чем то же количество в спокойном состоянии. Таким образом, объём абсолютной пустоты может рассматриваться как эквивалент энергии.

Тяготение, гравитация, гравитационное взаимодействие, универсальное взаимодействие между любыми видами материи. Если это взаимодействие относительно слабое и тела движутся медленно (по сравнению со скоростью света), то справедлив закон всемирного тяготения Ньютона. В общем случае тяготение описывается созданной А. Эйнштейном общей теорией относительности. Эта теория описывает тяготение как воздействие материи на свойства пространства и времени; в свою очередь, эти свойства пространства-времени влияют на движение тел и др. физические процессы. Таким образом, современная теория тяготение резко отличается от теории других видов взаимодействия - электромагнитного, сильного и слабого.

Теория тяготения Ньютона

Первые высказывания о тяготении как всеобщем свойстве тел относятся к античности. Так, Плутарх писал: "Луна упала бы на Землю как камень, чуть только уничтожилась бы сила её полёта".

В 16 и 17 вв. в Европе возродились попытки доказательства существования взаимного тяготения тел. Основатель теоретической астрономии И. Кеплер говорил, что "тяжесть есть взаимное стремление всех тел". Итальянский физик Дж. Борелли пытался при помощи тяготения объяснить движение спутников Юпитера вокруг планеты. Однако научное доказательство существования всемирного тяготения и математическая формулировка описывающего его закона стали возможны только на основе открытых И. Ньютоном законов механики. Окончательная формулировка закона всемирного тяготения была сделана Ньютоном в вышедшем в 1687 главном его труде "Математические начала натуральной философии". Ньютона закон тяготения гласит, что две любые материальные частицы с массами mА и mВ притягиваются по направлению друг к другу с силой F, прямо пропорциональной произведению масс и обратно пропорциональной квадрату расстояния r между ними.

Ньютоновская теория тяготения и ньютоновская механика явились величайшим достижением естествознания. Они позволяют описать с большой точностью обширный круг явлений, в том числе движение естественных и искусственных тел в Солнечной системе, движения в др. системах небесных тел: в двойных звёздах, в звёздных скоплениях, в галактиках. На основе теории тяготения Ньютона было предсказано существование неизвестной ранее планеты Нептун и спутника Сириуса и сделаны многие др. предсказания, впоследствии блестяще подтвердившиеся. В современной астрономии закон тяготения Ньютона является фундаментом, на основе которого вычисляются движения и строение небесных тел, их эволюция, определяются массы небесных тел. Точное определение гравитационного поля Земли позволяет установить распределение масс под её поверхностью (гравиметрическая разведка) и, следовательно, непосредственно решать важные прикладные задачи. Однако в некоторых случаях, когда поля тяготения становятся достаточно сильными, а скорости движения тел в этих полях не малы по сравнению со скоростью света, тяготения уже не может быть описано законом Ньютона.

Необходимость обобщения закона тяготения Ньютона Теория Ньютона предполагает мгновенное распространение тяготения и уже поэтому не может быть согласована со специальной теорией относительности (см. Относительности теория), утверждающей, что никакое взаимодействие не может распространяться со скоростью, превышающей скорость света в вакууме. Нетрудно найти условия, ограничивающие применимость ньютоновской теории тяготения. Так как эта теория не согласуется со специальной теорией относительности, то её нельзя применять в тех случаях, когда гравитационные поля настолько сильны, что разгоняют движущиеся в них тела до скорости порядка скорости света с. Скорость, до которой разгоняется тело, свободно падающее из бесконечности (предполагается, что там оно имело пренебрежимо малую скорость) до некоторой точки, равна по порядку величины корню квадратному из модуля гравитационного потенциала j в этой точке (на бесконечности j считается равным нулю). Таком образом, теорию Ньютона можно применять только в том случае, если

|j| << c2.

В полях тяготения обычных небесных тел это условие выполняется: так, на поверхности Солнца |j|/c2 " 4×10-6, а на поверхности белых карликов - порядка 10-3.

Обобщение теории тяготения на основе специальной теории относительности было сделано А. Эйнштейном в 1915-16 гг. Новая теория была названа её творцом общей теорией относительности.

Принцип эквивалентности. Самой важной особенностью поля тяготения, известной в ньютоновской теории и положенной Эйнштейном в основу его новой теории, является то, что тяготения совершенно одинаково действует на разные тела, сообщая им одинаковые ускорения независимо от их массы, химического состава и др. свойств. Так, на поверхности Земли все тела падают под влиянием её поля тяготения с одинаковым ускорением - ускорением свободного падения. Этот факт был установлен опытным путём ещё Г. Галилеем и может быть сформулирован как принцип строгой пропорциональности гравитационной, или тяжёлой, массы mT, определяющей взаимодействие тела с полем тяготения, и инертной массы mИ, определяющей сопротивление тела действующей на него силе и входящей во второй закон механики Ньютона. Действительно, уравнение движения тела в поле тяготения записывается в виде:

mИа = F = mTg,

где а - ускорение, приобретаемое телом под действием напряжённости гравитационного поля g. Если mИ пропорциональна mТ и коэффициент пропорциональности одинаков для любых тел, то можно выбрать единицы измерения так, что этот коэффициент станет равен единице, mИ = mТ; тогда они сокращаются в уравнении (6), и ускорение а не зависит от массы и равно напряжённости g поля тяготения, а = g, в согласии с законом Галилея.

Таким образом, тела разной массы и природы движутся в заданном поле тяготения совершенно одинаково, если их начальные скорости были одинаковыми. Этот факт показывает глубокую аналогию между движением тел в поле тяготения и движением тел в отсутствие тяготения, но относительно ускоренной системы отсчёта. Так, в отсутствие тяготения тела разной массы движутся по инерции прямолинейно и равномерно. Если наблюдать эти тела, например, из кабины космического корабля, который движется вне полей тяготения с постоянным ускорением за счёт работы двигателя, то, естественно, по отношению к кабине все тела будут двигаться с постоянным ускорением, равным по величине и противоположным по направлению ускорению корабля. Движение тел будет таким же, как падение с одинаковым ускорением в постоянном однородном поле тяготения. Силы инерции, действующие в космическом корабле, летящем с ускорением, равным ускорению свободного падения на поверхности Земли, неотличимы от сил гравитации, действующих в истинном поле тяготения в корабле, стоящем на поверхности Земли. Следовательно, силы инерции в ускоренной системе отсчёта (связанной с космическим кораблём) эквивалентны гравитационному полю. Этот факт выражается принципом эквивалентности Эйнштейна. Согласно этому принципу, можно осуществить и процедуру обратную описанной выше имитации поля тяготения ускоренной системой отсчёта, а именно, можно "уничтожить" в данной точке истинное гравитационное поле введением системы отсчёта, движущейся с ускорением свободного падения. Действительно, хорошо известно, что в кабине космического корабля, свободно (с выключенными двигателями) движущегося вокруг Земли в её поле тяготения, наступает состояние невесомости - не проявляются силы тяготения. Эйнштейн предположил, что не только механическое движение, но и вообще все физические процессы в истинном поле тяготения, с одной стороны, и в ускоренной системе в отсутствие тяготения, с другой стороны, протекают по одинаковым законам. Этот принцип получил название "сильного принципа эквивалентности" в отличие от "слабого принципа эквивалентности", относящегося только к законам механики.

Основная идея теории тяготения Эйнштейна

Рассмотренная выше система отсчёта (космический корабль с работающим двигателем), движущаяся с постоянным ускорением в отсутствие поля тяготения, имитирует только однородное гравитационное поле, одинаковое по величине и направлению во всём пространстве. Но поля тяготения, создаваемые отдельными телами, не таковы. Для того чтобы имитировать, например, сферическое поле тяготения Земли, нужны ускоренные системы с различным направлением ускорения в различных точках. Наблюдатели в разных системах, установив между собой связь, обнаружат, что они движутся ускоренно друг относительно друга, и тем самым установят отсутствие истинного поля тяготения. Таким образом, истинное поле тяготения не сводится просто к введению ускоренной системы отсчёта в обычном пространстве, или, говоря точнее, в пространстве-времени специальной теории относительности. Однако Эйнштейн показал, что если, исходя из принципа эквивалентности, потребовать, чтобы истинное гравитационное поле было эквивалентно локальным соответствующим образом, ускоренным в каждой точке системам отсчёта, то в любой конечной области пространство-время окажется искривленным - неевклидовым. Это означает, что в трёхмерном пространстве геометрия, вообще говоря, будет неевклидовой (сумма углов треугольника не равна p, отношение длины окружности к радиусу не равно 2p и т.д.), а время в разных точках будет течь по-разному. Таким образом, согласно теории тяготения Эйнштейна, истинное гравитационное поле является не чем иным, как проявлением искривления (отличия геометрии от евклидовой) четырёхмерного пространства-времени.

Следует подчеркнуть, что создание теории тяготения Эйнштейна стало возможным только после открытия неевклидовой геометрии русским математиком Н. И. Лобачевским, венгерским математиком Я. Больяй, немецкими математиками К. Гауссом и Б. Риманом.

В отсутствие тяготения движение тела по инерции в пространстве-времени специальной теории относительности изображается прямой линией, или, на математическом языке, экстремальной (геодезической) линией. Идея Эйнштейна, основанная на принципе эквивалентности и составляющая основу теории тяготения, заключается в том, что и в поле тяготения все тела движутся по геодезическим линиям в пространстве-времени, которое, однако, искривлено, и, следовательно, геодезические линии уже не прямые.

Массы, создающие поле тяготения, искривляют пространство-время. Тела, которые движутся в искривленном пространстве-времени, и в этом случае движутся по одним и тем же геодезическим линиям независимо от массы или состава тела. Наблюдатель воспринимает это движение как движение по искривленным траекториям в трёхмерном пространстве с переменной скоростью. Но с самого начала в теории Эйнштейна заложено, что искривление траектории, закон изменения скорости - это свойства пространства-времени, свойства геодезических линий в этом пространстве-времени, а, следовательно, ускорение любых различных тел должно быть одинаково, и, значит, отношение тяжёлой массы к инертной одинаково для всех тел, и эти массы неотличимы. Таким образом, поле тяготения, по Эйнштейну, есть отклонение свойств пространства-времени от свойств плоского (не искривлённого) многообразия специальной теории относительности.

Вторая важная идея, лежащая в основе теории Эйнштейна, - утверждение, что тяготение, то есть искривление пространства-времени, определяется не только массой вещества, слагающего тело, но и всеми видами энергии, присутствующими в системе. Эта идея явилась обобщением на случай теории тяготения принципа эквивалентности массы (m) и энергии (Е) специальной теории относительности, выражающейся формулой Е = mс2. Согласно этой идее, тяготения зависит не только от распределения масс в пространстве, но и от их движения, от давления и натяжений, имеющихся в телах, от электромагнитного поля и всех др. физических полей.

Наконец, в теории тяготения Эйнштейна обобщается вывод специальной теории относительности о конечной скорости распространения всех видов взаимодействия. Согласно Эйнштейну, изменения гравитационного поля распространяются в вакууме со скоростью с.

Уравнения тяготения Эйнштейна

В специальной теории относительности в инерциальной системе отсчёта квадрат четырёхмерного "расстояния" в пространстве-времени (интервала ds) между двумя бесконечно близкими событиями записывается в виде:

ds2= (cdt)2 - dx2- dy2 - dz2

где t - время, х, у, z - прямоугольные декартовы (пространственные) координаты. Эта система координат называется галилеевой. Выражение имеет вид, аналогичный выражению для квадрата расстояния в евклидовом трёхмерном пространстве в декартовых координатах (с точностью до числа измерений и знаков перед квадратами дифференциалов в правой части). Такое пространство-время называют плоским, евклидовым, или, точнее, псевдоевклидовым, подчёркивая особый характер времени: в выражении перед (cdt)2 стоит знак "+", в отличие от знаков "-" перед квадратами дифференциалов пространственных координат. Таким образом, специальная теория относительности является теорией физических процессов в плоском пространстве-времени (пространстве-времени Минковского).

В пространстве-времени Минковского не обязательно пользоваться декартовыми координатами, в которых интервал записывается в виде. Можно ввести любые криволинейные координаты. Тогда квадрат интервала ds2 будет выражаться через эти новые координаты общей квадратичной формой:

ds2 = gikdx idx k

(i, k = 0, 1, 2, 3), где x 1, x 2, x 3- произвольные пространств, координаты, x0 = ct - временная координата (здесь и далее по дважды встречающимся индексам производится суммирование). С физической точки зрения переход к произвольным координатам означает и переход от инерциальной системы отсчёта к системе, вообще говоря, движущейся с ускорением (причём в общем случае разным в разных точках), деформирующейся и вращающейся, и использование в этой системе не декартовых пространственных координат. Несмотря на кажущуюся сложность использования таких систем, практически они иногда оказываются удобными. Но в специальной теории относительности всегда можно пользоваться и галилеевой системой, в которой интервал записывается особенно просто.

В общей теории относительности пространство-время не плоское, а искривленное. В искривленном пространстве-времени (в конечных, не малых, областях) уже нельзя ввести, декартовы координаты, и использование криволинейных координат становится неизбежным.

При наличии поля тяготения величина g₀₀ в разных точках разная, следовательно, темп течения времени зависит от поля тяготения. Оказывается, что чем сильнее поле, тем медленнее течёт время по сравнению с течением времени для наблюдателя вне поля.

Математическим аппаратом, изучающим неевклидову геометрию (см. Риманова геометрия) в произвольных координатах, является тензорное исчисление. Общая теория относительности использует аппарат тензорного исчисления, её законы записываются в произвольных криволинейных координатах (это означает, в частности, запись в произвольных системах отсчёта), как говорят, в ковариантном виде.

Основная задача теории тяготения - определение гравитационного поля, что соответствует в теории Эйнштейна нахождению геометрии пространства-времени. Эта последняя задача сводится к нахождению метрического тензора gik.

Вскоре после создания общей теории относительности Эйнштейн показал (1917), что существует возможность изменения уравнений с сохранением основных принципов новой теории. Это изменение состоит в добавлении к правой части уравнений так называемого "космологического члена": Lgik. Постоянная L, называется "космологической постоянной", имеет размерность см-2. Целью этого усложнения теории была попытка Эйнштейна построить модель Вселенной, которая не изменяется со временем. Космологический член можно рассматривать как величину, описывающую плотность энергии и давление (или натяжение) вакуума. Однако вскоре (в 20-х гг.) советский математик А. А. Фридман показал, что уравнения Эйнштейна без L-члена приводят к эволюционирующей модели Вселенной, а американский астроном Э. Хаббл открыл (1929) закон так называемого красного смещения для галактик, которое было истолковано как подтверждение эволюционной модели Вселенной. Идея Эйнштейна о статической Вселенной оказалась неверной, и хотя уравнения с L-членом тоже допускают нестационарные решения для модели Вселенной, необходимость в L-члене отпала. После этого Эйнштейн пришёл к выводу, что введение L-члена в уравнения тяготения не нужно (то есть что L = 0). Не все физики согласны с этим заключением Эйнштейна. Но следует подчеркнуть, что пока нет никаких серьёзных наблюдательных, экспериментальных или теоретических оснований считать L отличным от нуля. Во всяком случае, если L ¹ 0, то, согласно астрофизическим наблюдениям, его абсолютная величина чрезвычайно мала: |L|< 10-55 см-2. Он может играть роль только в космологии и практически совершенно не сказывается во всех др. задачах теории тяготения. Везде в дальнейшем будет положено L = 0.

Экспериментальная проверка теории Эйнштейна

В основе теории тяготения Эйнштейна лежит принцип эквивалентности. Его проверка с возможно большей точностью является важнейшей экспериментальной задачей. Согласно принципу эквивалентности, все тела независимо от их состава и массы, все виды материи должны падать в поле тяготения с одним и тем же ускорением. Справедливость этого утверждения, как уже говорилось, была впервые установлена Галилеем. Венгерский физик Л. Этвеш с помощью крутильных весов доказал справедливость принципа эквивалентности с точностью до 10-8; американский физик Р. Дикке с сотрудниками довёл точность до 10-10, а советский физик В. Б. Брагинский с сотрудниками - до 10-12.

Другой проверкой принципа эквивалентности является вывод об изменении частоты n света при его распространении в гравитационном поле. Теория предсказывает  изменение частоты Dn при распространении между точками с разностью гравитационных потенциалов j1 - j2.

Эксперименты в лаборатории подтвердили эту версию с точностью по крайней мере до 1%.

Кроме этих экспериментов по проверке основ теории, существует ряд опытных проверок её выводов. Теория предсказывает искривление луча света при прохождении вблизи тяжёлой массы. Аналогичное отклонение следует и из ньютоновской теории тяготения, однако теория Эйнштейна предсказывает вдвое больший эффект. Многочисленные наблюдения этого эффекта при прохождении света от звёзд вблизи Солнца (во время полных солнечных затмений) подтвердили предсказание теории Эйнштейна (отклонение на 1,75?? у края солнечного диска) с точностью около 20%. Гораздо большая точность была достигнута с помощью современной техники наблюдения внеземных точечных радиоисточников. Этим методом предсказание теории подтверждено с точностью (на 1974) не меньшей 6%.

Др. эффектом, тесно связанным с предыдущим, является большая длительность времени распространения света в поле тяготения, чем это дают формулы без учёта эффектов теории Эйнштейна. Для луча, проходящего вблизи Солнца, эта дополнительная задержка составляет около 2×10-4 сек. Эксперименты проводились с помощью радиолокации планет Меркурий и Венера во время их прохождения за диском Солнца, а также с помощью ретрансляции радиолокационных сигналов космическими кораблями. Предсказания теории подтверждены (на 1974) с точностью 2%.

Наконец, ещё одним эффектом является предсказываемый теорией Эйнштейна медленный дополнительный (не объясняемый гравитационными возмущениями со стороны др. планет Солнечной системы) поворот эллиптических орбит планет, движущихся вокруг Солнца. Наибольшую величину этот эффект имеет для орбиты Меркурия - 43?? в столетие. Это предсказание подтверждено экспериментально, согласно современным данным, с точностью до 1%.

Таким образом, все имеющиеся экспериментальные данные подтверждают правильность как положений, лежащих в основе теории тяготения Эйнштейна, так и её наблюдательных предсказаний.

Следует подчеркнуть, что эксперименты свидетельствуют против попыток построить другие теории тяготения, отличные от теории Эйнштейна.

В заключение отметим, что косвенным подтверждением теории тяготения Эйнштейна является наблюдаемое расширение Вселенной, теоретически предсказанное на основе общей теории относительности советским математиком А. А. Фридманом в середине 20-х гг. нашего столетия.[2]

2. Электростатическое поле и его свойства

Электрическое поле создается электрическими зарядами или заряженными телами, а также действует на эти объекты независимо от того, движутся они или неподвижны. Если электрически заряженные частицы или тела неподвижны в данной системе отсчета, то их взаимодействие осуществляется посредством электростатического поля.

Электростатическое поле – вид матери, осуществляющий взаимодействие между электрически заряженными частицами.[3]

Силовой   (векторной)   характеристикой   электрического   поля является напряженность поля   :  , где   - сила, действующая на положительный заряд q, помещенный в данную точку поля.

Напряженность электростатического поля в некоторой его точке численно равна силе, действующей на неподвижный положительный пробный заряд, который не искажает того поля, которое с его помощью изучается. При этом его собственным электрическим полем пренебрегают.

Единица напряженности - вольт на метр, [Е] = 1В/м, Сила, действующая на заряд q, помещенный в любое электрическое поле с напряженностью , .

Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.

Электрическое поле называется однородным, если вектор его напряженности   одинаков во всех точках поля, в противном случае неоднородным. Примерами однородных полей   являются электростатические поля равномерно заряженной конечной плоскости и плоского конденсатора вдали от краев его обкладок.

Электрическое поле, напряженность которого не изменяется с течением времени, называется стационарным (постоянным). Например, стационарными являются электростатические поля — поля, создаваемые неподвижными зарядами.

Поле, работа которого при перемещении заряда по любой замкнутой траектории равна нулю, называют потенциальным. Пример потенциального поля - электростатическое поле.

Экспериментальная проверка закона Кулона

Закон установлен Кулоном в 1785 г. посредством прямых измерений сил взаимодействия между заряженными телами, размеры которых много меньше расстояния между ними. При этом точность опытов была небольшая. Лишь из общих соображений, основанных на аналогии с силами тяготения, существовала уверенность в абсолютной правильности этого закона. Но закон Кулона входит в число основных экспериментальных фактов, на которых построено учение об электричестве. Проверка его справедливости и установление границ применимости являются важнейшими задачами, на решение которых значительные усилия экспериментаторов направлялись вплоть до сегодняшних дней.

Ограничимся рассмотрением самого простого, доступного метода проверки закона Кулона – метода Кавендиша, оставляя новые методы, базирующиеся на новых физических теориях, в стороне.

Итак, метод Кавендиша. Интересно, что Кавендиш открыл «закон Кулона» за 15 лет до Кулона значительно более оригинальным методом, но свои результаты не опубликовал. Идея Кавендиша состояла в том, чтобы проверить, остается ли электрическое поле внутри заряженной проводящей сферы. Со времен Ньютона было известно, что если силы взаимодействия обратно пропорциональны квадрату расстояния, то внутри сферического слоя поле должно равняться нулю. Поэтому отсутствие поля внутри заряженной сферы означало бы, что электростатические силы, как и гравитационные, обратно пропорциональны квадрату расстояния.

Опыт ставился следующим образом. На заряженный проводящий шар накладывались две проводящие полусферы, плотно пригнанные друг к другу. Затем полусферы убирались и с помощью обычного электроскопа измерялся остаточный потенциал шара, который оказался равным нулю в пределах точки эксперимента.

Для лучшего понимания метода Кавендиша решим такую вспомогательную задачу. Считая, что электрическое поле точечного заряда q, находящегося в начале координат, задается выражением

E→(r→) = qf(r)r→ r ,

где r→ – радиус-вектор точки наблюдения, выяснить, при какой функции f(r) электрическое поле внутри однородно заряженной сферы равно нулю.

Пусть R0 – радиус сферы, σ – поверхностная плотность зарядов. Через точку наблюдения P внутри сферы и центр сферы проведем ось z (рис. 26). Выделим на сфере кольцо, определяемое сферическим углом ν с шириной R0dν. Заряд этого кольца

dq = 2πR02 sinνdν ⋅ σ.

Нетрудно увидеть, что в точке P кольцо создает электрическое поле, имеющее только z — компоненту.

dEz = −dq ⋅ f(r)cosθ,

где r = r(ν) – расстояние от точек кольца до точки наблюдения P, θ – угол, показанный на рисунке.

Поле от всей сферы находится интегрированием по всем кольцам

Ez = −2πR02σ ∫ 0πf(r)sinνcosθdν.

В интеграле перейдем к новой переменной интегрирования r, воспользовавшись геометрическими соотношениями

r2 = R 02 + r 02 − 2R 0r0 cosν,(а)

r0 + rcosθ = R0 cosν.(б)

Из (а) имеем

sinνdν = rdr R0r0,(в)

и

R0 cosν = R02 + r02 − r2 2r0 ,

и из (б) получаем

cosθ = R0 cosν − r0 r ,

что с учетом предыдущего выражения дает

cosθ = R02 − r02 − r2 2r0r .(г)

С использованием соотношений (в), (г) выражение для Ez приобретает вид

Ez = −πR0 r02 σ ∫ R0−r0R0+r0 (R02 − r 02 − r2)f(r)dr.

Теперь вспомним – задача заключается в определении функции f(r), обеспечивающей выполнение условия Ez = 0. Следовательно, имеем интегральное уравнение

∫ R0−r0R0+r0 (R02 − r 02 − r2)f(r)dr = 0.

Пусть f(r) = Φ′(r). Тогда

∫ R0−r0R0+r0 = ∫ R0−r0R0+r0 (R02 − r 02 − r2)f(r)Φ′(r)dr

и интегрируя по частям, получим

∫ R0−r0R0+r0 = (R02−r 02−r2)Φ(r)∣ R0−r0R0+r0 +2∫ R0−r0R0+r0 Φ(r)rdr = [R02−r 02−(R 0+r0)2]Φ(R 0+r0)−[R02−r 02−(R 0−r0)2]Φ(R 0−r0)+2∫ R0−r0R0+r0 Φ(r)rdr =  −2r0(R0+r0)Φ(R0+r0)−2r0(R0−r0)Φ(R0−r0)+2∫ R0−r0R0+r0 Φ(r)rdr = 0.

Интегральное уравнение перепишем, вводя обозначения R1 = R0 − r0, R2 = R0 + r0, откуда r0 = R2−R1 2 ; получим

∫ R1R2 Φ(r) ⋅ rdr = (R2 − R1) ⋅R1Φ(R1) + R2Φ(R2) 2 .(д)

Интеграл в левой части (д) можно заменить выражением [Φ(r) ⋅ r]ср ⋅ (R2 − R1), где нижний индекс означает взятие среднего значения функции на интервале [R1,R2]. В результате имеем

[Φ(r) ⋅ r]ср ⋅ (R2 − R1) = (R2 − R1) ⋅R1Φ(R1) + R2Φ(R2) 2 ,т.е.

[Φ(r) ⋅ r]ср = R1Φ(R1) + R2Φ(R2) 2 .

При любых R1,R2 среднее значение функции на интервале [R1,R2] равно полусумме крайних значений на интервале только в том случае, если эта функция линейная, т.е.

Φ(r) ⋅ r = κ0 + κ1r,Φ(r) = κ0 r + κ1.

Отсюда искомая функция

f(r) = Φ′(r) = −κ0 r2 ,κ0 = const.

Только при f(r) ∼ 1 r2 поле внутри равномерно заряженной сферы тождественно равно нулю.

Итак, если в опыте Кавендиша после снятия двух полусфер заряд шара точно равняется нулю, то из этого следует, что закон Кулона абсолютно точен. К сожалению, экспериментатор никогда не сможет сказать, что заряд точно равен нулю. Он может указать только, что заряд меньше некоторой малой величины и отсюда делают вывод о величине малой добавки ɛ в показателе, если закон Кулона представить в виде

E = q r2+ɛ.[4]

3. Модель объединения полей

Рассмотрим в качестве первого шага статический случай, т. е. взаимодействие покоящихся тел. Принято считать, что при электростатическом взаимодействии тел выполняется принцип близкодействия, согласно которому одно заряженное тело испытывает воздействие другого через электростатическое поле, которое выступает как реальная самостоятельная сущность. Это означает, что при взаимодействии участвуют два различных объекта: поле и заряд. В соответствии с этим в аналитической записи закона электростатического взаимодействия (ЗЭВ) должны присутствовать два различных параметра, один из которых характеризует способность тела создавать собственное электростатическое поле, а второй – его способность реагировать на внешние поля. Между тем в записи силы, действующей между двумя точечными объектами: телами или частицами с зарядами Q1 и Q2 , предложенной Кулоном

 (1)

кроме характеристик пространства: расстояния между зарядами r и диэлектрической проницаемости среды e, а также константы e0, зависящей от выбранной системы единиц, для каждого из тел имеется только одна характеристика — заряд Q, который одновременно описывает оба свойства тела. Несоответствие имеет исторические корни. Экспериментируя с заряженными телами, Кулон устанавливал зависимость электрических сил от различных параметров: от расстояния, а также величин и знаков зарядов без рассмотрения механизма взаимодействия заряженных тел в целом. Понятия поля в то время еще не существовало. В течение более двухсот лет закон безупречно работал на практике, и форма записи ЗЭВ постепенно стала представляться верной во всех отношениях.

Чтобы привести форму записи ЗЭВ, предложенную Кулоном, в соответствие с современным представлением о взаимодействии заряженных тел через их поля и не входить в противоречие с реальностью необходимо:

-     заменить в выражении (1) произведение равных в размерностях и по смыслу параметров Q на произведение двух различных, один из которых будет характеризовать создаваемое телом поле, а другой — способность тела реагировать на внешние поля;

-     учесть в аналитической записи требование симметрии ЗЭВ по отношению к телам.

Для решения данной задачи удобно принять следующие обозначения:

f — характеристика тела как источника поля с размерностью силы;

s — характеристика тела как объекта, на который действует поле, с размерностью площади.

С помощью новых параметров электростатическое взаимодействие двух точечных тел может быть записано в виде

 (2)

где f1, s1 и f2, s2 — параметры тела 1 и 2, соответственно. Как видно, размерность произведения fs совпадает с размерностью квадрата заряда, деленного на диэлектрическую постоянную.

Уравнение (2) можно интерпретировать следующим образом: тело 1 своим полем f1 воздействует на поверхность s2 тела 2, в то же время тело 2 своим полем f2 воздействует на поверхность s1 тела 1. Каждое тело вырезает из поля другого тела телесный угол s/r2, поэтому сила взаимодействия имеет обратную квадратичную зависимость от расстояния между телами.

Примем, что значения f, s макроскопического тела равны суммам значений тех же параметров составляющих его атомов и свободных электронов, а значения параметров атомов складываются из значений соответствующих параметров образующих его элементарных частиц. Для упрощения будем рассматривать макротело как ансамбль протонов и электронов, на которые разложим и нейтроны атомов. Для упрощения записи диэлектрическую проницаемость среды e положим равной единице.

Обозначим параметры протона через fр, sp, а параметры электрона — через fe, se. Используем скалярную запись ЗЭВ, в которой отрицательное значение силы будет соответствовать притяжению тел. Для согласования знаков сил примем, что fp, sp > 0, a fe, se < 0 . Для количественного соответствия традиционного выражения и (2) при записях протон-протонного, протон-электронного и электрон-электронного взаимодействий необходимо положить, что

 (3)

где е — элементарный заряд.

Представим теперь некоторое макроскопическое тело, состоящее из Np протонов и Ne электронов. Электрическое состояние тела — заряженность или нейтральность — будет характеризоваться параметром

DN = Np – Ne.

Если количество электронов в теле меньше числа протонов, то DN положительно, что соответствует положительной заряженности тела, и наоборот. Условие DN = 0 соответствует классическому понятию электрической нейтральности тела.

Рассмотрим силовое взаимодействие произвольно заряженного точечного тела с протоном, электроном и атомом водорода. Ввиду равенства в атоме водорода числа протонов и электронов он будет представлять нейтральное тело. В уравнении (2) эти взаимодействия будут иметь вид:

взаимодействие тела с протоном

 (4)

взаимодействие тела с электроном

 (5)

Складывая левые и правые части уравнений (4) и (5), получим выражение взаимодействия тела с атомом водорода

 (6)

Обозначая fр = – fе (1 + kf), sр = – sе (1 + ks),

где kf, ks — константы, и учитывая (3), соотношение (7) можно записать в виде

 (7)

Из выражения (7) следует, что в состоянии классического понятия нейтральности DN = 0, когда число электронов в теле в точности равно числу протонов, его электростатическое силовое взаимодействие c атомом водорода в общем случае не равно нулю:

 (8)

При kf ks < 0 сила взаимодействия отрицательна, что соответствует притяжению тел. Величина силы, как видно, пропорциональна числу протон-электронных пар, т. е. массе тела. Таким образом, полученное электростатическое взаимодействие электрически нейтральных, с классической точки зрения, тел может быть отождествлено с гравитационным.

 (9)

где G — гравитационная постоянная, а Mт, mн — массы тела и атома водорода, соответственно.

Для количественного согласования (9) с (8) достаточно положить

 (10)

Таким образом, константа гравитационного взаимодействия может быть выражена через известные и новые параметры

Выражение для гравитационного взаимодействия двух тел с массами М1 и М2 приобретает вид

 (11)

Помимо электростатического взаимодействия нейтральных тел новая запись центрального взаимодействия позволяет выявить неизвестное в настоящее время центральное взаимодействие двух тел, одно из которых заряжено, а другое — нейтрально. Это взаимодействие может быть названо смешанным. Действительно, согласно выражению (7), при kf + ks  0 между атомом водорода и телом действует сила, пропорциональная заряду тела eDN

 (12)

В случае двух макротел, одно из которых заряжено зарядом Q1, а другое c массой М2 — нейтрально, выражение (12) приобретает вид (положение между электростатическим и гравитационным).

 (13)

Таким образом, общее центральное взаимодействие двух тел может преимущественно проявляться различно в зависимости от степени их заряженности и величин масс, а именно как:

-   взаимодействие двух заряженных тел (электростатическое) (1);

-   взаимодействие заряженного тела с незаряженным (смешанное) (13);

-   взаимодействие незаряженных тел (гравитационное) (11) (рис. 1).

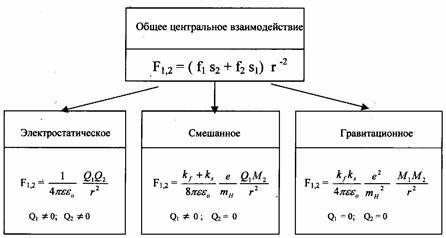
Рис. 1. Проявление общего центрального взаимодействия в зависимости от электрического состояния взаимодействующих тел

В понятиях заряда и массы в общем случае произвольно заряженных точечных тел взаимодействие может быть представлено в виде

Все три компоненты, как видно, оказываются одной природы, причем массы тел формально могут быть заменены некоторыми величинами зарядов.

Поясним графически причину появления эффекта притяжения электрически нейтральных тел. На рис. 2, а по оси X отложены значения DN тела, а по оси Y — величины силового взаимодействия тела с другими объектами. Сила взаимодействия тела с протоном обозначена наклонной прямой Fтр, проходящей через первый и третий квадранты и пересекающей ось Х в некоторой точке 1. Эта точка в общем может не совпадать с точкой пересечения осей. Силовое взаимодействие тела с электроном Fте представляется наклонной прямой, проходящей через второй и четвертый квадранты. Эта прямая пересекает ось Х в некоторой точке 2, которая также может не совпадать с пересечением осей. Наконец силовое взаимодействие тела с атомом водорода, которое является суммой взаимодействий тела с протоном и электроном, представляет собой прямую, параллельную оси Х. Можно убедиться, что когда точки 1 и 2 на оси Х не совпадают между собой, линия взаимодействия атома водорода с телом не совпадает с осью Х. Последнее означает, что электростатическое взаимодействие тела с атомом водорода не равно нулю при любых значениях заряда тела, в том числе при нейтральности тела относительно протонов. В этой точке нулевое взаимодействие с протоном компенсируется силой взаимодействия тела с электроном атома. Можно видеть также, что если взаимное пересечение прямых Fтр и Fте происходит ниже оси Х, то линия Fтн также проходит ниже нее, что соответствует эффекту притяжения телом атома водорода. Таким образом, обобщая результат, можно сделать вывод, что гравитация является компонентой электростатического взаимодействия, которая существует вследствие несовпадения состояний электрической нейтральности тела относительно протонов и электронов.

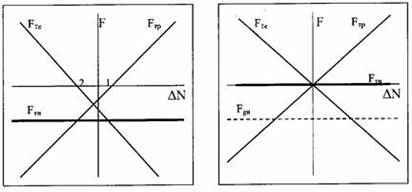
а         б

Рис. 2. Силовое взаимодействие произвольно заряженного тела с протоном Fтр, электроном Fте и атомом водорода Fтн в зависимости от величины и знака заряда:

а - в логике новой записи центрального взаимодействия; б - при классическом представлении. Fgн - гравитационное взаимодействие тела с атомом водорода

Несовпадение состояний нейтральности относительно двух частиц характеризуется величинами параметров kf, ks (10). Различие между этими состояниями мало и представляет преимущественно теоретический интерес.

Для сравнения на рис. 2, б приведены зависимости силового взаимодействия тела с протоном, электроном и атомом водорода, вытекающие из закона Кулона. Симметрично наклонные относительно оси Х прямые, обозначающие силовое взаимодействие протона и электрона, пересекаются между собой в точке пересечения осей. При таком представлении зависимостей электростатическое взаимодействие тела с атомом водорода оказывается тождественно равным нулю независимо от заряда тела. Это отображается прямой Fтн, совпадающей с осью Х. Классическое представление об электростатических взаимодействиях в варианте б привели к необходимости введения дополнительного поля — гравитационного, которое выглядело принципиально отличающимся от электростатического. На рис. 2, б гравитационное поле атома водорода представлено пунктирной линией Fgн.

Смешанная компонента, как можно заключить по характеру силового взаимодействия тела с атомом водорода, существует лишь при условии различия углов наклона относительно оси Х прямых, обозначающих взаимодействие протона и электрона с телом.[5]

Заключение

Использование ЗЭВ в уравнении (2) предполагает переход от понятий заряда и тяготеющей массы к параметрам f, s. Имеющиеся экспериментальные данные, накладывая на значения этих параметров некоторые ограничения, не позволяют в настоящее время определить их однозначно.

 При взаимодействиях они всегда выступают в виде произведений, ввиду чего предстоит отыскать способы раздельного определения их значений. Необходимо будет также установить, как они взаимоотносятся с известными константами.

Практически важным представляется вопрос о том, реализуется ли в природе смешанное взаимодействие. Существование его возможно при отличии от нуля суммы коэффициентов kf и ks, значения которых предстоит измерить. Однако информация о компоненте может быть получена экспериментально и без раздельного знания значения каждого коэффициента. Смешанная компонента может вносить заметные коррективы в практические расчеты, поэтому исследования в этом направлении представляются весьма актуальными.

Изложенный вариант объединения электростатического поля с гравитационным не противоречит экспериментальным данным о связи гравитации с неоднородностью (кривизной) пространства.

Из построений следует лишь, что в дальнейшем эффекты неоднородности пространства необходимо связывать с электростатическим полем. В частности, можно ожидать, что неоднородность пространства вблизи протона в его поле может быть сильнее неоднородности, проявляющейся в гравитационном поле атома водорода, в пропорции отношения сил смешанного взаимодействия протона с атомом водорода и гравитационных сил между двумя атомами водорода.

Новая форма записи ЗЭВ влечет за собой коррекцию представлений о физической сущности электромагнитного поля, что должно учитываться при дальнейшем развитии модели, т. е. при построении нестатической теории гравиэлектромагнитного взаимодействия.

Список литературы

1.                     Дягилев Ф.М. Концепции современного естествознания. - М.: ИМПЭ, 2004.

2.                     Концепции современного естествознания./Под ред. С.А. Самыгина. – Ростов-на-Дону: Феникс, 2003.

3.                     Логунов А. А. Теория классического гравитационного поля. – М.6 Дело, 2002.

4.                     Похмельных Л. А. Электростатика и гравитация как различные проявления общего центрального взаимодействия стабильных элементарных частиц//Прикладная физика, 2002, № 1. -  С. 24-32

5.                     Юхимец А.К. Физическая сущность специальной теории относительности. - Киев: КГУ, 2004.

[1] Дягилев Ф.М. Концепции современного естествознания. - М.: ИМПЭ, 2004. – С. 218

[2] Логунов А. А. Теория классического гравитационного поля. – М.: Дело, 2002. – С. 41

[3] Концепции современного естествознания./Под ред. С.А. Самыгина. – Ростов-на-Дону: Феникс, 2003. – С. 279

[4] Юхимец А.К. Физическая сущность специальной теории относительности. - Киев: КГУ, 2004. – С. 184

[5] Похмельных Л. А. Электростатика и гравитация как различные проявления общего центрального взаимодействия стабильных элементарных частиц//Прикладная физика, 2002, № 1. -  С. 24-32