Содержание
4. Какова связь между
динамическим и кинематическим коэффициентами вязкости? Какова их размерность в
единицах СИ и в единицах других систем измерения?. 3
15. Каков геометрический и физический смысл
пьезометрического и гидравлического уклонов? Могут ли они быть отрицательными?. 3
24. От каких факторов зависят гидравлические
сопротивления при ламинарном и турбулентном режимах движения? Как это связано
со структурой потока?. 4
34. Что представляют собой прямой и непрямой
гидравлические удары? Определение ударного повышения давления. 4
Задача 6. 6
Задача 7. 7
Задача 16. 8
Задача 27. 10
Задача 30. 11
Задача 36. 12
Список литературы.. 14
4. Какова связь между
динамическим и кинематическим коэффициентами вязкости? Какова их размерность в
единицах СИ и в единицах других систем измерения?
Вязкость жидкости –
физическая характеристика жидкости, определяющая свойства ее текучести.
Различают два вида вязкости:
·
Динамическая вязкость – коэффициент пропорциональности касательного напряжения
сдвига между слоями топлива перепаду скоростей движения этих слоев,
рассчитанному на единицу расстояния между ними (измеряется в сантипуазах: 1 сП
= 10-3 Па×с = 10-3 кг/м×с);
·
Кинематическая вязкость – отношение динамической вязкости к плотности топлива
(измеряется в сантистоксах: 1 сСт = 10-2 Ст = 10-6 м2/с). Чаще используют
именно эту характеристику, которую просто именуют вязкостью (по умолчанию –
измеренную при 20 °C окружающего воздуха).
Эти величины в системе СИ
имеют размерность кг/м×с. В других системах
вместо кг могут использоваться граммы, вместо метров – сантиметры или
миллиметры, вместо секунд – другие единицы времени.
15. Каков геометрический и
физический смысл пьезометрического и гидравлического уклонов? Могут ли они быть
отрицательными?
Геометрический уклон – угол наклона русла потока относительно горизонта.
При равномерном движении жидкости в открытом русле гидравлический iг и пьезометрический iп уклоны, а также уклон дна русла iп равны между собой:
iг = iп = iд
Пьезометрический и
гидравлический уклоны не могут быть отрицательными – это бы означало течение
жидкости в другую сторону.
24. От каких факторов
зависят гидравлические сопротивления при ламинарном и турбулентном режимах
движения? Как это связано со структурой потока?
В современной науке общепризнанны два режима движения
жидкости – ламинарный и турбулентный. Характерно различие между ламинарным
(параллельно струйным) и турбулентным (извилистым) режимами течения жидкостей.
Причиной образования любой извилистости является разность между тем, что может
делать предмет, и тем, что заставляют его делать.
ГИДРАВЛИЧЕСКОЕ (ГИДРОДИНАМИЧЕСКОЕ) СОПРОТИВЛЕНИЕ - сила,
возникающая при движении тела в жидкости или несжимаемом газе, а также при течении
жидкости или газа в канале.
Гидравлическое сопротивление зависит от структуры потока: при
ламинарном потоке слои жидкости перемещаются параллельно друг другу, при турбулентном
течении наблюдается смешение слоев, что увеличивает гидравлическое
сопротивление.
34. Что
представляют собой прямой и непрямой гидравлические удары? Определение ударного
повышения давления
Под понятием
"гидравлический удар" понимают резкое повышение давления , возникающее в упругом трубопроводе с
малосжимаемой жидкостью при внезапном изменении скорости ее течения.
Прямой гидравлический удар - физическое явление, вызывающее концентрированное повышение
давления на отдельном участке трубопровода. Непрямой гидравлический удар
возникает в результате отражения волны от прямого гидравлического удара от
некоторой поверхности (преграды), что ведет к уменьшению ударного давления.
Причиной гидравлического удара
является быстрое закрытие крана.
В качестве меры уменьшения негативных
последствий гидравлического удара используют замену прямого гидравлического
удара на непрямой. Для этого достаточно запорную арматуру на напорных
трубопроводах сделать медленно закрывающейся, что позволит уменьшить силу
удара.
Резкое увеличение давления,
сопровождающее гидравлический удар, называется ударным повышением давления.
Задача 6
Определить силу давления
на коническую крышку горизонтального цилиндрического сосуда диаметром D1=2000 мм, заполненного керосином. Показания манометра
в точке его присоединения – рм=0,4 МПА (абс). Показать на чертеже
вертикальную и горизонтальную составляющие, а также полную силу давления. а=1000
мм.
Решение:
Пусть
жидкость заполняет резервуар, правая стенка которого представляет собой
цилиндрическую криволинейную поверхность АВС (рис.1), простирающуюся в
направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО
к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится
в равновесии. Это значит, что силы, действующие на поверхности выделенного
объема V, и силы веса взаимно уравновешиваются.
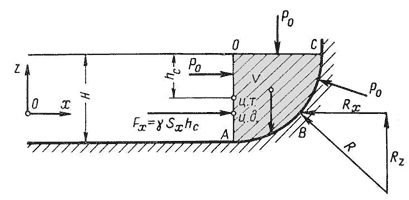
Рис. 1. Схема
гидростатического давления на цилиндрическую поверхность
На рисунке показаны
составляющие силы реакции стенки, которые равны по модулю, но противоположны по
направлению соответствующим компонентам силы давления
Cила
гидростатического давления на площадь Sx по направлению оси
Ох равна Fx = γ Sx hc , где
hc – высота центра давления, который находится по формуле
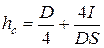 .
.
Площадь боковой
поверхности конуса 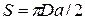 .
.
Плотность керосина γ
= 8000 Н/м3.
Тогда
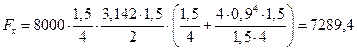 Н.
Н.
Аналогично находятся
остальные две составляющие этой силы – по осям Oy и Oz.
Тогда полная сила
давления:
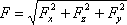 =
=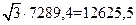 Н.
Н.
Ответ: полная сила
давления 12625,5 Н.
Задача 7
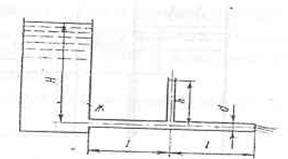
При истечении жидкости из
резервуара в атмосферу по горизонтальной трубе диаметром d=40 мм и длиной 2l = 4 м. Уровень в пьезометре, установленном посередине
трубы, равен h=3 м. Определить расход Q и коэффициент гидравлического трения l, если
статический напор в баке постоянен и равен Н. Построить пьезометрическую и
напорную линии. Сопротивлением жидкости в труб пренебречь.
Решение:
Искомый расход с учетом потерь в
соединительных трубах находится по формуле
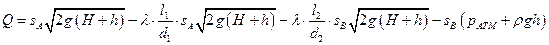 .
.
Выполним элементарные преобразования с этой формулой:
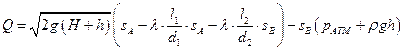 .
.
Подставим числовые значения:
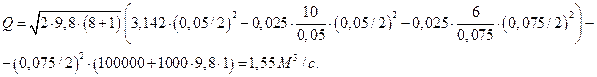
Для построения пьезометрических
линий, найдем пьезометрические высоты соответственно в точках А и В:
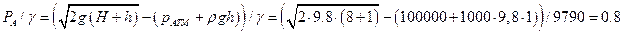 м.
м.
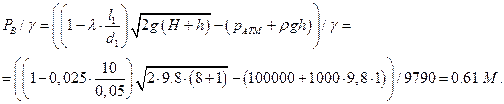
Тогда
пьезометрическая линия выглядит следующим образом:
Задача 16
Определить длину
трубы l, при которой расход жидкости из бака
будет ровно в два раза меньше, чем через отверстие того же бака диаметра d = 70 мм. Напор над отверстием
равен Н = 4 м. Коэффициент
гидравлического трения 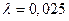 .
.
Решение:
Считаем, что отверстие в
стенке сосуда малое, т.к. 4м >> 70 мм, поэтому применима формула Торричелли,
согласно которой расход жидкости через отверстие площадью s
равен 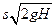 .
.
Если делать поправку на
сопротивление через насадок, каковым в задаче является труба, то формула
Торричелли изменится: 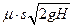 , где
, где 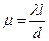 – коэффициент
сопротивления насадка
– коэффициент
сопротивления насадка
Так как, по условию
задачи, расход жидкости из бака будет ровно в два раза меньше, чем через
отверстие того же бака, то выразим искомую длину трубы из уравнения:
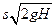 =
=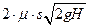 .
.
Выполняя элементарные
преобразования, получиv, что
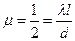
Искомая длина 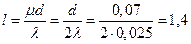 м.
м.
Схематично действие
искомых сил можно изобразить следующим образом:
На этой схеме F1 –
сила давления воды, F2 – сила трения, вызванная прохождение
воды внутри трубы.
Задача 27
Определить
производительность и напор насоса (рабочую точку) при подаче воды в открытый резервуар
из колодца на геодезическую высоту Нг = 6 м по трубопроводу
диаметром d = 250 мм, длиной l = 40 м, с коэффициентом
гидравлического трения 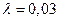 и эквивалентной длиной
местных сопротивлений lэкв = 8 м. Как изменится подача и напор
насоса, если частота вращения рабочего колеса уменьшится на 10%?
и эквивалентной длиной
местных сопротивлений lэкв = 8 м. Как изменится подача и напор
насоса, если частота вращения рабочего колеса уменьшится на 10%?
Решение:
Для развития максимальной
производительности насоса на уровне 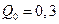 м3/с при необходимости подачи воды в открытый
резервуар из колодца на геодезическую высоту Нг = 6 м по
трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом
гидравлического трения
м3/с при необходимости подачи воды в открытый
резервуар из колодца на геодезическую высоту Нг = 6 м по
трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом
гидравлического трения 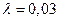 и эквивалентной длиной
местных сопротивлений lэкв = 8 м максимальный напор насоса
найдется из соотношения:
и эквивалентной длиной
местных сопротивлений lэкв = 8 м максимальный напор насоса
найдется из соотношения:
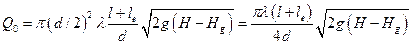 .
.
Выразим из этого
соотношения максимальный напор и подставим численные значения:
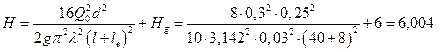 м.
м.
При расчете подачи и
напора насоса при изменении частоты вращения рабочего колеса на 10% следует
иметь в виду, что в таблице с исходными данными показана производительность
насоса с шагом 20%. Для ответа на поставленный вопрос составим таблицу с шагом
10%, исходя их предположения о линейной связи
Q – H на каждом 20%-ом отрезке; тогда
соответствующие коэффициенты в точках 0,1, 0,3, 0,5, 0,7, 0,9 найдутся как
средние арифметические соседних коэффициентов при Н:
|
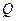
|
0
|
0.1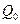
|
0.2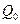
|
0.3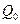
|
0,4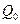
|
0,5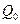
|
0,6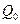
|
0,7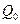
|
0,8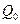
|
0,9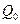
|
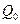
|
|
H
|
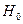
|
1,025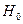
|
1,05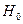
|
1,025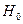
|
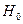
|
1,44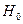
|
1,88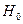
|
1,265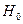
|
0,65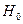
|
0,5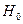
|
0,35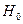
|
Так, при снижении
производительности с максимальной до 90% напор увеличится и составит:
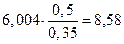 м.
м.
Для построения
характеристики "насос – сеть" задаемся рядом значений расхода,
вычисляем полные напоры, соответствующие этим расходам. При заданных значениях Q вычисляются
значения Н. После чего, на одном графике, в одном масштабе выполняются
построения характеристики Q-Н насоса и характеристик трубопроводов, далее
графически определяется (пересечением кривых) рабочий режим насоса.
|
Q
|
0,03
|
0,06
|
0,09
|
0,12
|
0,15
|
0,18
|
0,21
|
0,24
|
0,27
|
0,3
|
|
H
|
6,1541
|
6,3042
|
6,1541
|
6,004
|
8,64576
|
11,28752
|
7,59506
|
3,9026
|
3,002
|
2,1014
|


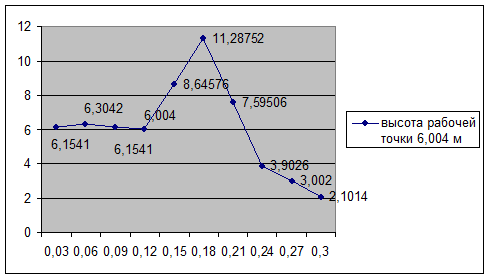
По горизонтальной оси
откладываются значения расхода воды. Пересечение графика Q-Н с горизонтальной линией,
показывающей рабочую точку насоса, показывает рабочий режим насоса –
приблизительно Q = 0,22 м3/с.
Задача 30
Поршневой насос простого
действия с диаметром цилиндра D=90 мм, ходом поршня S=260 мм, числом двойных ходов в
минуту п=75 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
систему гидропровода. При какой частоте вращения должен работать включенный
параллельно шестеренный насос с начальным диаметром шестерен d=72 мм, шириной шестерен b=65 мм, числом зубьев z=30 и объемным КПД hоб=0,86, чтобы количество подаваемой
жидкости удвоилось?
Решение:
Поршневой насос простого действия с
диаметром цилиндра D=90 мм, ходом поршня S=260 мм, числом двойных ходов в минуту п=75 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
количестве
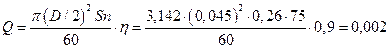 м3/мин.
м3/мин.
Для расчета минутной подачи насосов с
двумя одинаковыми шестернями можно пользоваться формулой
Q = η0A(Dг-
A)bN ,
где η0 - объемный КПД
насоса, зависящий от конструкции, технологии изготовления и давления насоса и
принимаемый равным 0,7-0,95; А - расстояние между центрами шестерен, равное
диаметру начальной окружности D; Dг - диаметр окружности головок
зубьев; b - ширина шестерен; N - частота вращения ротора, об/мин.
Согласно условию задачи,
количество подаваемой жидкости должно удвоиться, тогда искомая частота
вращения:
N = η0A(Dг-A)b /
(2∙Q) = = 50 об/мин.
Ответ: 50 об/мин.
Задача 36
Определить полезную
мощность насоса объемного действия гидропривода, если внешняя нагрузка на
поршень силового гидроцилиндра F = 70000 H, скорость рабочего хода
v = 12,5 см/с, диаметр поршня D1 = 130 мм, диаметр штока D2 = 44 мм. Механический коэффициент полезного действия
гидроцилиндра 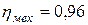 , объемный коэффициент полезного действия гидроцилиндра
, объемный коэффициент полезного действия гидроцилиндра 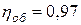 . Общая длина трубопровода системы l = 12 м, диаметр трубопроводов d = 25 мм. Рабочая жидкость в системе
– спиртоглицериновая смесь (Y = 12100 Н/м3, v = 1,2 см2/с).
. Общая длина трубопровода системы l = 12 м, диаметр трубопроводов d = 25 мм. Рабочая жидкость в системе
– спиртоглицериновая смесь (Y = 12100 Н/м3, v = 1,2 см2/с).
Указание: Напор насоса затрачивается на перемещение поршня, нагруженного силой F, и на преодоление гидравлических
потерь в трубопроводах системы.
Решение:
Полезную мощность насоса
можно найти по двум эквивалентным формулам:
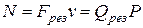 ,
,
где результирующая сила Fрез
посчитана с учетом механических и гидравлических потерь в трубопроводах системы; также эти потери
учитываются при расчете Qрез.
Поршень диаметром D1 = 130 мм, нагруженный силой 70000 H с учетом механических потерь,
создает давление
Р = 0,13 ×
70000 × 0,96 = 8736 Па.
Значит, это давление
двигает жидкость по трубопроводу системы, развивая мощность
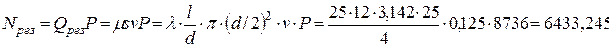 Вт.
Вт.
Наконец, учитывая
объемный коэффициент полезного действия, окончательно получим:
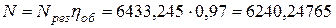 Вт.
Вт.
Ответ: 6240,25 Вт.
Список литературы
1.
Башта
Т.М., Руднев С.С. Гидравлика, гидромашины и гидропривод. – М.: Машиностроение,
1982.
2.
Дергачев
Ф.М. Основы гидравлики и гидропривод. – М.: Стройиздат, 1981.
3.
Задачник
по гидравлике, гидромашинам и гидроприводу / под ред. Б.Б. Некрасова. – М.:
Высшая школа, 1989.
4.
Осипов
П.Е. Гидравлика, гидромашины и гидропривод. – М.: Лесная промышленность, 1981.
5.
Юфин
А.П. Гидравлика, гидромашины и гидропривод. – М.: