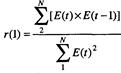ВАРИАНТ 1
Задача 1.
По
предприятиям легкой промышленности региона получена информация, характеризующая
зависимость объема выпуска продукции (![]() , млн. руб.) от объема капиталовложений (
, млн. руб.) от объема капиталовложений (![]() , млн. руб.)
, млн. руб.)
Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов;
оценить дисперсию остатков ![]() ; построить график остатков.
; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента ![]()
5. Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью ![]() - критерия Фишера
- критерия Фишера ![]() , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего значения
показателя ![]() при уровне
значимости
при уровне
значимости ![]() , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
7. Представить графически: фактические и модельные
значения ![]() точки прогноза.
точки прогноза.
8. Составить уравнения нелинейной регрессии:
· гиперболической;
· степенной;
· показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
|
|
66 |
58 |
73 |
82 |
81 |
84 |
55 |
67 |
81 |
59 |
|
|
133 |
107 |
145 |
162 |
163 |
170 |
104 |
132 |
159 |
116 |
1. Найдем параметры уравнения линейной регрессии, дадим экономическую интерпретацию коэффициента регрессии.
Уравнение линейной регрессии имеет вид: ![]()
Значения параметров а и b линейной модели определим, используя данные таблицы 1.1.
![]()
![]()
Уравнение линейной регрессии имеет вид: ![]() =-15,78+2,19*x.
=-15,78+2,19*x.
С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличиться в среднем на 2,19 млн. руб. Это свидетельствует об эффективности работы предприятия.
2. Вычислим остатки; найдем остаточную сумму квадратов;
оценим дисперсию остатков ![]() ; построим график остатков.
; построим график остатков.
Остатки см табл 1.1 столбец ![]()
Остаточная сумма квадратов ![]() =59,51
=59,51
Дисперсия остатков 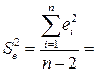 59.51/8=7.44
59.51/8=7.44
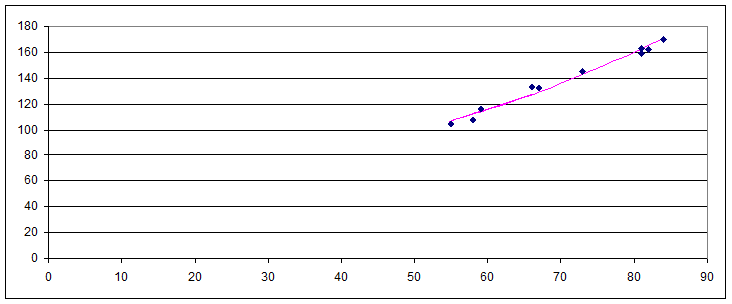
График остатков
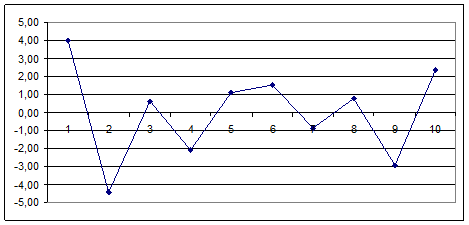
3. Проверим выполнение предпосылок МНК.
Проверка выполнения предпосылок МНК выполняется на основе анализа остаточной компоненты.
- случайный характер остатков
- нулевая средняя величина остатков, не зависящая от от xi
- гомоскедастичность – дисперсия каждого отклонения ei одинакова для всех значений x
- отсутствие автокорреляции остатков
- остатки подчиняются нормальному распределению
случайный характер остатков
с этой целью строится график зависимости остатков ei от теоретических значений результативного признака
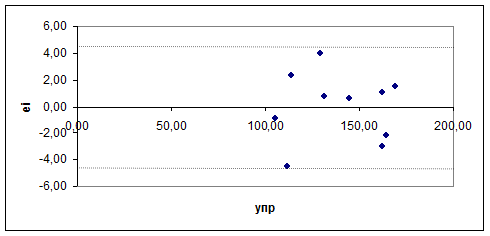
На графике получена горизонтальная полоса, значит остатки ei представляют собой случайные величины и МНК оправдан
нулевая средняя величина остатков, не зависящая от xi
с этой целью строится график зависимости остатков ei от факторов, включенных в регрессию xi.
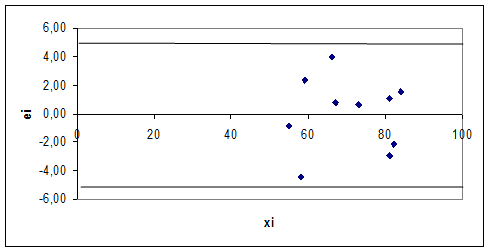
Остатки на графике расположены в виде горизонтальной полосы, значит они не зависимы от xi.
Проверка равенства
математического ожидания уровней ряда остатков нулю осуществляется в ходе
проверки соответствующей нулевой гипотезы H0: ![]() . С этой целью строится t-статистика
. С этой целью строится t-статистика 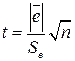 , где
, где 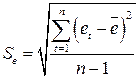 .
.
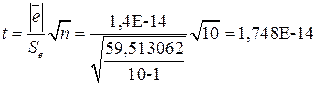
![]() гипотеза принимается.
гипотеза принимается.
|
t-статистика |
1,748E-14 |
||
|
t крит 0,05 |
2,228 |
||
|
t |
ei=yi-yi^ |
(ei-ei cp)^2 |
|
|
1 |
3,991292 |
15,93041 |
|
|
2 |
-4,45864 |
19,879432 |
|
|
3 |
0,634978 |
0,4031974 |
|
|
4 |
-2,10885 |
4,4472627 |
|
|
5 |
1,084906 |
1,1770203 |
|
|
6 |
1,503628 |
2,2608985 |
|
|
7 |
-0,87736 |
0,7697579 |
|
|
8 |
0,797533 |
0,6360583 |
|
|
9 |
-2,91509 |
8,497775 |
|
|
10 |
2,347605 |
5,5112503 |
|
|
Сумма |
-1,4E-13 |
59,513062 |
|
|
Среднее |
-1,4E-14 |
гомоскедастичность – дисперсия каждого отклонения ei одинакова для всех значений x
Коэфф. Спирмена 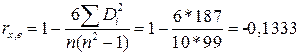 где
где ![]()
t-статистика 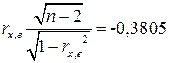 это меньше t
Крит, следовательно гипотеза об отсутствии гетероскедастичности при
пятипроцентном уровне значимости принимается
это меньше t
Крит, следовательно гипотеза об отсутствии гетероскедастичности при
пятипроцентном уровне значимости принимается
|
К проверке предпосылки МНК №3 по тесту Спирмена |
|||
|
r(x) |
r(e) |
r(x)-r(e) |
(r(x)-r(e))^2 |
|
4 |
9 |
-5 |
25 |
|
2 |
10 |
-8 |
64 |
|
6 |
1 |
5 |
25 |
|
9 |
6 |
3 |
9 |
|
7 |
4 |
3 |
9 |
|
10 |
5 |
5 |
25 |
|
1 |
3 |
-2 |
4 |
|
5 |
2 |
3 |
9 |
|
7 |
8 |
-1 |
1 |
|
3 |
7 |
-4 |
16 |
|
Сумма |
187 |
||
|
Коэфф. Спирмена |
-0,1333 |
||
|
t-статистика |
-0,3805 |
||
|
t крит 0,05 |
2,306 |
Гомоскедастичность присутствует
Независимость остатков проверяется с помощью критерия Дарбина – Уотсона.
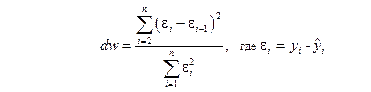
dw=165,20/59,51=2,77 dw’=4-2.77=1.23
Верхние (d2=1.32) и нижние (d1=0.88) критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции, зависят от количества уровней динамического ряда и числа независимых переменных модели.
Если 0<d<d1, то уровни автокоррелированы, то есть зависимы, модель неадекватна.
Если d1<d<d2, то критерий Дарбина-Уотсона не дает ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней по первому коэффициенту автокорреляции).
Если d2<d<2 , то уровни ряда остатков являются независимыми.
В нашем случае d1 < dw <d2 – критерий Дарбина-Уотсона не дает ответа на вопрос о независимости уровней ряда остатков. Проверим независимость уровней по первому коэффициенту автокорреляции
|
|
=-33,81/59,51= -0,568 |
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения |r(1)|<rтаб, то уровни ряда остатков независимы. Для нашей задачи критический уровень rтаб = 0,36. Имеем: |r(1)| =0.56> rтаб = 0,36 - значит уровни зависимы.
нормальности распределения остаточной компоненты по R/S-критерию с критическими уровнями 2.67-3.685;
Рассчитаем значение RS: RS = (Emax - Emin)/ S,
где Emin - максимальное значение уровней ряда остатков E(t);
Emax - минимальное значение уровней ряда остатков E(t)
S - среднее квадратическое отклонение.
![]()
|
Emax= |
3,99 |
|
Emin= |
-4,46 |
|
Emax-Emin= |
8,45 |
|
S= |
2,57149 |
|
RS= |
3,286004 |
Так как 2,67<3,28<3.685, полученное значение RS попало в заданный интервал. Значит, уровни ряда остатков подчиняются нормальному распределению.
Таким образом предпосылки МНК не выполняются.
4. Осуществим проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента ![]()
Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t–статистики) для соответствующих коэффициентов регрессии:
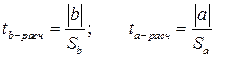
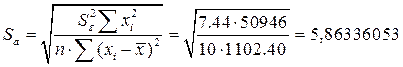
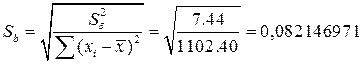
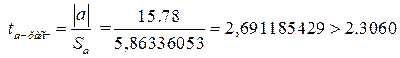
![]()
Затем расчетные значения ![]() сравниваются с табличными tтабл=2,3060. Табличное значение критерия определяется при
(n-2) степенях свободы (n - число наблюдений) и соответствующем
уровне значимости a (0,05)
сравниваются с табличными tтабл=2,3060. Табличное значение критерия определяется при
(n-2) степенях свободы (n - число наблюдений) и соответствующем
уровне значимости a (0,05)
Если расчетное значение t-критерия с (n - 2) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым.
В нашем случае коэффициенты регрессии значимы.
5. Вычислим коэффициент детерминации, проверить
значимость уравнения регрессии с помощью ![]() - критерия Фишера
- критерия Фишера ![]() , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Определим линейный коэффициент парной корреляции по формуле
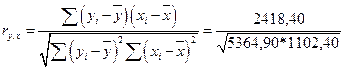 =0,994
=0,994
Рассчитаем коэффициент детерминации:
![]() 0.9942 =0,989
0.9942 =0,989
Вариация результата Y (объема выпуска продукции) на 98,9 % объясняется вариацией фактора X (объемом капиталовложений).
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:
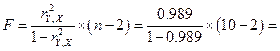 713,173
713,173
F>Fтабл.=5.32 для α=0,05; k1=m=1; k2=n-m-1=8
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F > Fтабл.
Определим среднюю относительную ошибку:
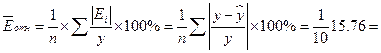 1,57%
1,57%
В среднем расчетные значения у для линейной модели отличаются от фактических значений на 1,57%
6. Осуществим прогнозирование среднего значения
показателя ![]() при уровне
значимости
при уровне
значимости ![]() , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
Прогнозное значение показателя, если прогнозное значение фактора
составит 80% от его максимального значения ![]() 0,8*84=67,20 составит
0,8*84=67,20 составит
![]() =-15,78+2,19*67,20=131,64
=-15,78+2,19*67,20=131,64
Интервальный прогноз:
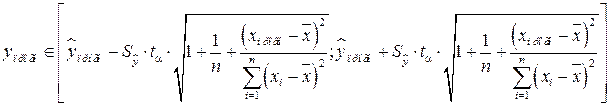
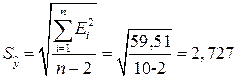
![]() для
для ![]() степеней свободы и
уровня значимости 0,1 равно 1,8595.
степеней свободы и
уровня значимости 0,1 равно 1,8595.
Тогда
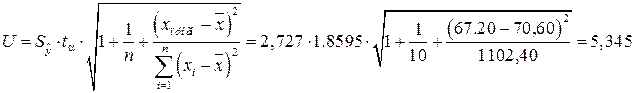
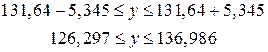
![]()
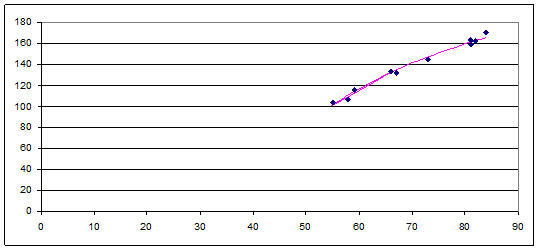
7. Представим графически: фактические и модельные
значения ![]() точки прогноза.
точки прогноза.
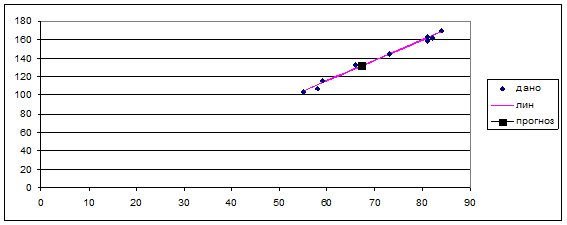
Таблица 1.1.
|
n |
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
133 |
66 |
8778 |
4356 |
-6,10 |
37,21 |
-4,60 |
21,16 |
129,01 |
3,99 |
15,93 |
- |
- |
3,00 |
28,06 |
|
2 |
107 |
58 |
6206 |
3364 |
-32,10 |
1030,41 |
-12,60 |
158,76 |
111,46 |
-4,46 |
19,88 |
71,40 |
-17,80 |
4,17 |
404,46 |
|
3 |
145 |
73 |
10585 |
5329 |
5,90 |
34,81 |
2,40 |
5,76 |
144,37 |
0,63 |
0,40 |
25,94 |
-2,83 |
0,44 |
14,16 |
|
4 |
162 |
82 |
13284 |
6724 |
22,90 |
524,41 |
11,40 |
129,96 |
164,11 |
-2,11 |
4,45 |
7,53 |
-1,34 |
1,30 |
261,06 |
|
5 |
163 |
81 |
13203 |
6561 |
23,90 |
571,21 |
10,40 |
108,16 |
161,92 |
1,08 |
1,18 |
10,20 |
-2,29 |
0,67 |
248,56 |
|
6 |
170 |
84 |
14280 |
7056 |
30,90 |
954,81 |
13,40 |
179,56 |
168,50 |
1,50 |
2,26 |
0,18 |
1,63 |
0,88 |
414,06 |
|
7 |
104 |
55 |
5720 |
3025 |
-35,10 |
1232,01 |
-15,60 |
243,36 |
104,88 |
-0,88 |
0,77 |
5,67 |
-1,32 |
0,84 |
547,56 |
|
8 |
132 |
67 |
8844 |
4489 |
-7,10 |
50,41 |
-3,60 |
12,96 |
131,20 |
0,80 |
0,64 |
2,81 |
-0,70 |
0,60 |
25,56 |
|
9 |
159 |
81 |
12879 |
6561 |
19,90 |
396,01 |
10,40 |
108,16 |
161,92 |
-2,92 |
8,50 |
13,78 |
-2,32 |
1,83 |
206,96 |
|
10 |
116 |
59 |
6844 |
3481 |
-23,10 |
533,61 |
-11,60 |
134,56 |
113,65 |
2,35 |
5,51 |
27,70 |
-6,84 |
2,02 |
267,96 |
|
итого |
1391,00 |
706,00 |
100623,00 |
50946,00 |
0,00000 |
5364,90 |
0,00 |
1102,40 |
|
0,00 |
59,51 |
165,20 |
-33,81 |
15,76 |
2418,40 |
|
ср. знач |
139,10 |
70,60 |
10062,30 |
5094,60 |
|
|
|
|
|
|
|
|
1,58 |
|
|
|
диспер |
624,24 |
120,49 |
|
|
|
|
|
|
|
6,61 |
|
|
|
|
8. Составим уравнения нелинейной регрессии:
· гиперболической;
· степенной;
· показательной.
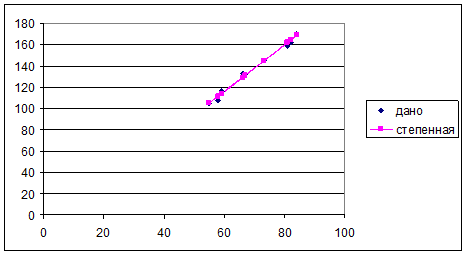
Приведем графики построенных уравнений регрессии.
9. Для указанных моделей найдем коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравним модели по этим характеристикам и сделаем вывод.
Построение степенной модели парной регрессии
Уравнение степенной модели имеет вид:![]() .
.
Для построения этой модели необходимо произвести линеаризацию
переменных. Для этого произведем логарифмирование обеих частей уравнения: lg ![]() = lg a + b lg x.
= lg a + b lg x.
|
|
Факт Y(t) |
lg(Y) |
Переменная X(t) |
lg(X) |
|
1 |
133 |
2,124 |
66 |
1,820 |
|
2 |
107 |
2,029 |
58 |
1,763 |
|
3 |
145 |
2,161 |
73 |
1,863 |
|
4 |
162 |
2,210 |
82 |
1,914 |
|
5 |
163 |
2,212 |
81 |
1,908 |
|
6 |
170 |
2,230 |
84 |
1,924 |
|
7 |
104 |
2,017 |
55 |
1,740 |
|
8 |
132 |
2,121 |
67 |
1,826 |
|
9 |
159 |
2,201 |
81 |
1,908 |
|
10 |
116 |
2,064 |
59 |
1,771 |
|
итого |
1391,00 |
21,370 |
706,00 |
18,439 |
|
сред знач |
139,10 |
2,137 |
70,60 |
1,844 |
Обозначим ![]() . Тогда уравнение примет вид: Y=А + b X — линейное уравнение регрессии.
. Тогда уравнение примет вид: Y=А + b X — линейное уравнение регрессии.
Рассчитаем его параметры, используя данные таблицы 1.2.
|
|
1,1276 |
|
|
0,0579 |
Уравнение регрессии будет иметь вид : Y=0,0579+1,1276X.
Перейдем к исходным переменным ли у, выполнив потенцирование данного уравнения.
![]()
Получим уравнение степенной модели регрессии:
![]() .
.
Определим индекс
корреляции: 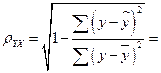 0,994
0,994
Связь между показателем у и фактором х достаточно сильная.
Коэффициент детерминации равен ![]() 0,988
0,988
Вариация результата Y (объема выпуска продукции) на 98,8% объясняется вариацией фактора X (объемом капиталовложений).
Рассчитаем F-критерий
Фишера: ![]() 671,55
671,55
F>F табл =5.32 Уравнение регрессии с вероятностью 0,95 в целом статистически значимое .
Средняя относительная ошибка 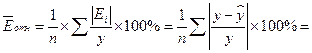 1.62%
1.62%
В среднем расчетные значения ![]() для степенной модели
отличаются от фактических значений на 1.62%.
для степенной модели
отличаются от фактических значений на 1.62%.
Таблица 1.2.
|
|
y |
Y |
x |
X |
YX |
X^2 |
y |
Ei |
E1/y*x*100% |
Ei2 |
|
1 |
133 |
2,1239 |
66 |
1,8195 |
3,86 |
3,31 |
128,7057 |
4,294 |
3,229 |
18,441 |
|
2 |
107 |
2,0294 |
58 |
1,7634 |
3,58 |
3,11 |
111,2556 |
-4,256 |
3,977 |
18,110 |
|
3 |
145 |
2,1614 |
73 |
1,8633 |
4,03 |
3,47 |
144,1991 |
0,801 |
0,552 |
0,641 |
|
4 |
162 |
2,2095 |
82 |
1,9138 |
4,23 |
3,66 |
164,3977 |
-2,398 |
1,480 |
5,749 |
|
5 |
163 |
2,2122 |
81 |
1,9085 |
4,22 |
3,64 |
162,1388 |
0,861 |
0,528 |
0,742 |
|
6 |
170 |
2,2304 |
84 |
1,9243 |
4,29 |
3,70 |
168,9260 |
1,074 |
0,632 |
1,154 |
|
7 |
104 |
2,0170 |
55 |
1,7404 |
3,51 |
3,03 |
104,7885 |
-0,789 |
0,758 |
0,622 |
|
8 |
132 |
2,1206 |
67 |
1,8261 |
3,87 |
3,33 |
130,9067 |
1,093 |
0,828 |
1,195 |
|
9 |
159 |
2,2014 |
81 |
1,9085 |
4,20 |
3,64 |
162,1388 |
-3,139 |
1,974 |
9,852 |
|
10 |
116 |
2,0645 |
59 |
1,7709 |
3,66 |
3,14 |
113,4209 |
2,579 |
2,223 |
6,652 |
|
Итого |
1391,00 |
21,3702 |
706,00 |
18,4386 |
39,45285 |
34,04188 |
|
0,12212 |
16,18241 |
63,15749 |
|
Сред знач |
139,1000 |
2,1370 |
70,6000 |
1,8439 |
3,9453 |
3,4042 |
|
|
1,6182 |
|
Построение показательной функции
Уравнение показательной кривой: у =abx . Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
lg ![]() = lg a + х lg b. Обозначим: Y = lg
= lg a + х lg b. Обозначим: Y = lg ![]() , В = lg b, A = lg a. Получим линейное уравнение
регрессии:
, В = lg b, A = lg a. Получим линейное уравнение
регрессии:
Y = А + В х. Рассчитаем его параметры, используя данные таблицы 1.3
![]()
![]()
Уравнение будет иметь вид: Y=1.639+0.007X Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения:
![]()
![]()
Определим индекс корреляции:
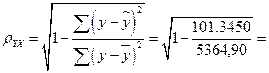 0.99
0.99
Связь между показателем у и фактором x: сильная.
Коэффициент детерминации: R2 =0.992 =0.981.
Вариация результата Y (объема выпуска продукции) на 98,1% объясняется вариацией фактора X(объемом капиталовложений).
Рассчитаем F-критерий Фишера:
![]() 415,49
415,49
F >F табл Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, .
Средняя относительная ошибка
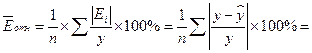 2,15
2,15
В среднем расчетные значения ![]() для показательной
модели отличаются от фактических значений на
для показательной
модели отличаются от фактических значений на
2,15%.
таблица 1.3
|
t |
y |
Y |
x |
Yx |
x^2 |
Y-Y |
(Y-Y)2 |
x-x |
(x-x)2 |
y |
(y-y)2 |
Ei |
E1/y*x*100% |
|
1 |
133 |
2,1239 |
66 |
140,17 |
4356,00 |
-0,0132 |
0,0002 |
-4,6000 |
21,1600 |
127,2237 |
33,3656 |
5,776 |
4,343 |
|
2 |
107 |
2,0294 |
58 |
117,70 |
3364,00 |
-0,1076 |
0,0116 |
-12,6000 |
158,7600 |
111,7189 |
22,2684 |
-4,719 |
4,410 |
|
3 |
145 |
2,1614 |
73 |
157,78 |
5329,00 |
0,0243 |
0,0006 |
2,4000 |
5,7600 |
142,5457 |
6,0236 |
2,454 |
1,693 |
|
4 |
162 |
2,2095 |
82 |
181,18 |
6724,00 |
0,0725 |
0,0053 |
11,4000 |
129,9600 |
164,9873 |
8,9238 |
-2,987 |
1,844 |
|
5 |
163 |
2,2122 |
81 |
179,19 |
6561,00 |
0,0752 |
0,0056 |
10,4000 |
108,1600 |
162,3287 |
0,4506 |
0,671 |
0,412 |
|
6 |
170 |
2,2304 |
84 |
187,36 |
7056,00 |
0,0934 |
0,0087 |
13,4000 |
179,5600 |
170,4358 |
0,1899 |
-0,436 |
0,256 |
|
7 |
104 |
2,0170 |
55 |
110,94 |
3025,00 |
-0,1200 |
0,0144 |
-15,6000 |
243,3600 |
106,4048 |
5,7832 |
-2,405 |
2,312 |
|
8 |
132 |
2,1206 |
67 |
142,08 |
4489,00 |
-0,0164 |
0,0003 |
-3,6000 |
12,9600 |
129,3073 |
7,2504 |
2,693 |
2,040 |
|
9 |
159 |
2,2014 |
81 |
178,31 |
6561,00 |
0,0644 |
0,0041 |
10,4000 |
108,1600 |
162,3287 |
11,0802 |
-3,329 |
2,094 |
|
10 |
116 |
2,0645 |
59 |
121,80 |
3481,00 |
-0,0726 |
0,0053 |
-11,6000 |
134,5600 |
113,5487 |
6,0091 |
2,451 |
2,113 |
|
Итого |
1391,00 |
21,3702 |
706,00 |
1516,51494 |
50946,00000 |
|
0,0561 |
|
1102,4000 |
1390,8296 |
101,3450 |
0,17037 |
21,51710 |
|
Сред знач |
139,1000 |
2,1370 |
70,6000 |
151,6515 |
5094,6000 |
|
|
|
|
|
|
|
2,1517 |
Построение гиперболической функции
Уравнение гиперболической функции: у = а + b/х . Произведем линеаризацию модели путем замены Х= 1/х. В результате получим линейное уравнение у = а + b X. Рассчитаем его параметры
![]()
![]()
Получим следующее
уравнение гиперболической модели: ![]() 288,8262-10330,3/x
288,8262-10330,3/x
Определим индекс корреляции:
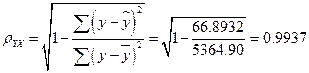
Связь между показателем у и фактором х сильная.
Коэффициент детерминации равен ![]() 0,987
0,987
Вариация результата Y (объема выпуска продукции) на 98,7% объясняется вариацией фактора X (объемом капиталовложений).
Рассчитаем F-критерий Фишера:
![]() 396,0048
396,0048
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F>F табл .
Средняя относительная ошибка
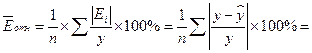 1,788%
1,788%
таблицы 1.4.
|
t |
y |
x |
X |
yX |
X^2 |
y-y |
(y-y)2 |
y |
Ei |
(y-y)2 |
E1/y*x*100% |
|
1 |
133 |
66 |
0,0152 |
2,02 |
0,0002296 |
-6,1000 |
37,2100 |
132,3068 |
0,693 |
0,4806 |
0,521 |
|
2 |
107 |
58 |
0,0172 |
1,84 |
0,0002973 |
-32,1000 |
1030,4100 |
110,7179 |
-3,718 |
13,8226 |
3,475 |
|
3 |
145 |
73 |
0,0137 |
1,99 |
0,0001877 |
5,9000 |
34,8100 |
147,3155 |
-2,315 |
5,3614 |
1,597 |
|
4 |
162 |
82 |
0,0122 |
1,98 |
0,0001487 |
22,9000 |
524,4100 |
162,8471 |
-0,847 |
0,7176 |
0,523 |
|
5 |
163 |
81 |
0,0123 |
2,01 |
0,0001524 |
23,9000 |
571,2100 |
161,2918 |
1,708 |
2,9178 |
1,048 |
|
6 |
170 |
84 |
0,0119 |
2,02 |
0,0001417 |
30,9000 |
954,8100 |
165,8466 |
4,153 |
17,2504 |
2,443 |
|
7 |
104 |
55 |
0,0182 |
1,89 |
0,0003306 |
-35,1000 |
1232,0100 |
101,0029 |
2,997 |
8,9827 |
2,882 |
|
8 |
132 |
67 |
0,0149 |
1,97 |
0,0002228 |
-7,1000 |
50,4100 |
134,6429 |
-2,643 |
6,9848 |
2,002 |
|
9 |
159 |
81 |
0,0123 |
1,96 |
0,0001524 |
19,9000 |
396,0100 |
161,2918 |
-2,292 |
5,2525 |
1,441 |
|
10 |
116 |
59 |
0,0169 |
1,97 |
0,0002873 |
-23,1000 |
533,6100 |
113,7367 |
2,263 |
5,1227 |
1,951 |
|
Итого |
1391,00 |
706,00 |
0,14 |
19,64817 |
0,0021504 |
|
5364,9000 |
1391,0000 |
0,00000 |
66,8932 |
17,88337 |
|
Сред знач |
139,1000 |
70,6000 |
0,0145 |
1,9648 |
0,0002150 |
|
|
|
|
|
1,7883 |
Для выбора лучшей модели построим сводную таблицу результатов.
Таблица 3.9
|
Параметры Модель |
Коэффициент детерминации R2 |
F-критерий Фишера |
Индекс корреляции |
Средняя относительная ошибка Eотн |
|
Линейная |
0,989 |
713,173 |
0,994 |
1,576267 |
|
Степенная |
0,988228 |
671,5583 |
0,994096 |
1,618241 |
|
Показательная |
0,98111 |
415,4958 |
0,99051 |
2,15171 |
|
Гиперболическая |
0,987531 |
396,0048 |
0,993746 |
1,788337 |
Все модели имеют примерно одинаковые характеристики, но большее значение коэффициента детерминации R2 и меньшее значение относительной ошибка Eотн имеет линейная модель. Ее можно взять в качестве лучшей для построения прогноза
Задача 2.
Задача 2а и 2б. Для каждого варианта даны по две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.
|
Номер варианта |
Номер уравнения |
Задача 2а |
||||||
|
переменные |
||||||||
|
у1 |
у2 |
у3 |
х1 |
х2 |
х3 |
x4 |
||
|
1 |
1 |
-1 |
b12 |
b13 |
0 |
0 |
a13 |
a14 |
|
2 |
0 |
-1 |
b23 |
a21 |
a22 |
a23 |
0 |
|
|
3 |
0 |
b32 |
-1 |
a31 |
0 |
a33 |
a34 |
Задача 2а
запишем системы одновременных уравнений
y1= b12 y2 + b13 y3 +a13 x3 + a14 x4
y2= b23 y3 +a21 x1 + a22 x2 + a23 x3
y3= b32y2 + a31 x1 +a33 x3 + a34 x4
Проверим каждое уравнение системы на выполнение неоходимого и достаточного условия идентификации.
В этих уравнениях присутствуют переменных следующих типов:
-эндогенные, зависимые переменные y, определяемые внутри системы;
-экзогенные, независимые переменные x, значения которых задаются извне, они являются управляемыми, планируемыми;
-предопределенные переменные, включающие в себя как экзогенные переменные за текущий период времени, так и лаговые переменные (т.е. экзогенные и эндогенные переменные за предыдущие периоды времени).
Для того, чтобы СФМ была идентифицируема, необходимо чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной формы.
Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой. В этом случае число коэффициентов приведенной формы модели меньше, чем число коэффициентов СФМ.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае можно получить два и более значений одного структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы.
Если обозначить число эндогенных переменных в i-том уравнении СФМ через Н, а число предопределенных переменных, которые содержатся в системе, но не входят в данное уравнение через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:
если D+1 < H уравнение неидентифицируемо;
если D+1 = H уравнение идентифицируемо;
если D+1 > H уравнение сверхидентифицируемо;
Счетное правило является необходимым, но не достаточным условием идентификации. Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие.
Отметим в системе эндогенные и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу. При этом если переменная стоит в левой части уравнения, то коэффициент надо брать с обратным знаком. Если определитель полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие индетификации для данного уравнения выполнено.
В первом уравнении три эндогенных переменных: y1 ,y2 и y3 (H=3). В нем отсутствуют экзогенные переменные x1 и x2 (D=2). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x1 и x2 (см. таблицу 2.1). В первом столбце таблицы показано, что коэффициенты при экзогенных переменных x1 и x2 взяты из уравнений 2 и 3 системы. Во втором уравнении эти переменные присутствуют и коэффициенты при них равны a21 и a22 соответственно. Определитель представленной в таблице 2.1 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и первое уравнение идентифицируемо.
Таблица 2.1
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
x1 |
x2 |
|
|
2 |
a21 |
a22 |
|
3 |
a31 |
0 |
Во втором уравнении две эндогенные переменные: y2 и y3 (H=2). В нем отсутствует экзогенная переменная x4 (D=1). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных y1 и x4 , которые отсутствуют во втором уравнении (см. таблицу 2.2).
Таблица 2.2
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
y1 |
x4 |
|
|
1 |
-1 |
a14 |
|
3 |
0 |
a34 |
Определитель представленной в таблице 2.2 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.
В третьем уравнении две эндогенные переменные: ,y2 и y3 (H=2). В нем отсутствует экзогенные переменные x2 (D=1). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных y1 и x2 , которые отсутствуют в третьем уравнении (см. таблицу 2.3).
Определитель представленной в таблице 2.3 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и третье уравнение идентифицируемо.
Таблица 2.3
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
y1 |
x2 |
|
|
1 |
-1 |
0 |
|
2 |
0 |
a22 |
Каждое уравнение системы идентифицируемо, значит СФМ идентифицируема
Задача 2б
|
Номер варианта |
Номер уравнения |
Задача 2б |
||||||
|
переменные |
||||||||
|
у1 |
у2 |
у3 |
х1 |
х2 |
х3 |
x4 |
||
|
1 |
1 |
-1 |
b12 |
b13 |
0 |
a12 |
a13 |
0 |
|
2 |
0 |
-1 |
b23 |
a21 |
a22 |
0 |
a24 |
|
|
3 |
b31 |
b32 |
-1 |
0 |
a32 |
a33 |
0 |
запишем системы одновременных уравнений
y1= b12 y2 + b13 y3 + a12 x2 +a13 x3
y2= b23 y3 +a21 x1 + a22 x2 + a24 x4
y3= b31y1 + b32y2 + a31 x1 + a32 x2 +a33 x3
Проверим каждое уравнение системы на выполнение неоходимого и достаточного условия идентификации.
В первом уравнении три эндогенных переменных: y1 ,y2 и y3 (H=3). В нем отсутствуют экзогенные переменные x1 и x4 (D=2). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x1 и x4 (см. таблицу 2.4). Определитель представленной в таблице 2.1 матрицы равен нулю, а ранг матрицы равен 1. Значит, достаточное условие не выполнено, и первое уравнение неидентифицируемо.
Таблица 2.4
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
x1 |
x4 |
|
|
2 |
a21 |
a24 |
|
3 |
0 |
0 |
Во втором уравнении две эндогенные переменные: y2 и y3 (H=2). В нем отсутствует экзогенная переменная x4 (D=1). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных y1 и x3 , которые отсутствуют во втором уравнении (см. таблицу 2.5).
Таблица 2.5
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
y1 |
x3 |
|
|
1 |
-1 |
a13 |
|
3 |
b31 |
a33 |
Определитель представленной в таблице 2.5 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.
В третьем уравнении три эндогенные переменные: y1, y2 и y3 (H=3). В нем отсутствует экзогенные переменные x1 и x4 (D=2). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x1 и x4 , которые отсутствуют в третьем уравнении (см. таблицу 2.6).
Определитель представленной в таблице 2.6 матрицы равен нулю, а ранг матрицы равен 1. Значит, достаточное условие не выполнено, и второе уравнение неидентифицируемо.
Таблица 2.6
|
Уравнения, из которых взяты коэффициенты при переменных |
Переменные |
|
|
x1 |
x4 |
|
|
1 |
0 |
0 |
|
2 |
a21 |
a24 |
Так как 1 и 3 уравнение системы неидентифицируемо, значит СФМ неидентифицируема
Задача 2в
По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида
y1= a01 + b12 y2 + a11 x1 + e1
y2= a02 + b21 y1 + a22 x2 + e2
Рассмотрим косвенный метод наименьших квадратов (КМНК) , который применяется в случае точно идентифицируемой структурной модели. Рассмотрим идентифицируемая модель, содержит две эндогенные и две экзогенные переменные:
y1= b12 y2 + a11 x1 + e1
y2= b21 y1 + a22 x2 + e2
Для построения модели мы располагаем информацией, представленной в таблице
Таблица 2.7.
|
n |
у1 |
у2 |
х1 |
х2 |
|
1 |
76,7 |
35,4 |
5 |
7 |
|
2 |
94,1 |
37,9 |
7 |
7 |
|
3 |
88,2 |
40,8 |
6 |
9 |
|
4 |
126,9 |
47,3 |
10 |
10 |
|
5 |
111,0 |
61,5 |
7 |
18 |
|
6 |
50,1 |
26,6 |
3 |
4 |
|
средн |
91,167 |
41,583 |
6,333 |
9,167 |
Структурную модель преобразуем в приведенную форму модели.
y1= d11 x1 + d12 x2 + u1
y2= d21 x1 + d22 x2 + u2
u1 и u1 – случайные ошибки.
Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК.
Для упрощения расчетов можно работать с отклонениями от средних уровней y=y-ycp и x=x-xcp (ycp и xcp –средние значения). Преобразованные таким образом данные таблицы 2.7 сведены в таблицу 2.8. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов dik. Переменные, означающие отклонение от средних значений изображаются далее жирным шрифтом и курсивом.
Для нахождения коэффициентов d1k первого приведенного уравнения можно использовать следующую систему нормальных уравнений:
Σ y1 x1= d11 Σ x12 + d12 Σ x1 x2
Σ y1 x2= d11 Σ x1 x2 + d12 Σ x22
Таблица 2.8
Преобразованные данные для построения приведенной формы модели
|
n |
у1 |
у2 |
х1 |
х2 |
у1*х1 |
х12 |
х1*х2 |
у1*х2 |
у2*х1 |
у2*х2 |
х22 |
|
1 |
-14,467 |
-6,183 |
-1,333 |
-2,167 |
19,289 |
1,778 |
2,889 |
31,344 |
8,244 |
13,397 |
4,694 |
|
2 |
2,933 |
-3,683 |
0,667 |
-2,167 |
1,956 |
0,444 |
-1,444 |
-6,356 |
-2,456 |
7,981 |
4,694 |
|
3 |
-2,967 |
-0,783 |
-0,333 |
-0,167 |
0,989 |
0,111 |
0,056 |
0,494 |
0,261 |
0,131 |
0,028 |
|
4 |
35,733 |
5,717 |
3,667 |
0,833 |
131,022 |
13,444 |
3,056 |
29,778 |
20,961 |
4,764 |
0,694 |
|
5 |
19,833 |
19,917 |
0,667 |
8,833 |
13,222 |
0,444 |
5,889 |
175,194 |
13,278 |
175,931 |
78,028 |
|
6 |
-41,067 |
-14,983 |
-3,333 |
-5,167 |
136,889 |
11,111 |
17,222 |
212,178 |
49,944 |
77,414 |
26,694 |
|
Сумма |
0,00000 |
0,0000 |
0,00000 |
0,00000 |
303,367 |
27,333 |
27,667 |
442,633 |
90,233 |
279,617 |
114,833 |
Подставляя рассчитанные в таблице 5.5 значения сумм, получим
|
303,367 |
= |
27,333 |
d11 |
+ |
27,667 |
d12 |
|
442,633 |
= |
27,667 |
d11 |
+ |
114,833 |
d12 |
Решение этих уравнений дает значения
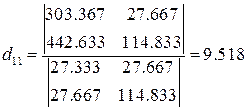
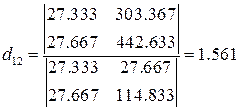
Первое уравнение приведенной формы модели примет вид
y1= 9,518 x1 + 1,561 x2 + u1
Для нахождения коэффициентов d2k второго приведенного уравнения можно использовать следующую систему нормальных уравнений:
Σ y2 x1= d21 Σ x12 + d22 Σ x1 x2
Σ y2 x2= d21 Σ x1 x2 + d22 Σ x22
Подставляя рассчитанные в таблице 2.8 значения сумм, получим
|
90,233 |
= |
27,333 |
d21 |
+ |
27,667 |
d22 |
|
279,617 |
= |
27,667 |
d21 |
+ |
114,833 |
d22 |
Решение этих уравнений дает значения
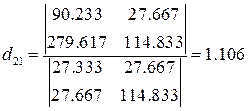
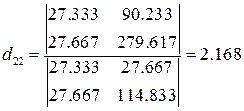
Второе уравнение приведенной формы модели примет вид
y2= 1,106x1 + 2,168 x2 + u2
Для перехода от приведенной формы к структурной форме модели найдем x2 из второго уравнения приведенной формы модели
|
x2 = |
(y2 - |
1,106 |
x1 ) / |
2,168 |
Подставим это выражение в первое уравнение приведенной модели, найдем структурное уравнение
|
y1= |
9,518 |
x1 |
+ |
1,561 |
(y2 - |
1,106 |
x1 ) / |
2,168 |
= |
|
= |
9,518 |
x1 |
+ |
0,720 |
y2 |
-0,79659 |
x1 |
= |
|
= |
0,720 |
y2 |
+ |
8,722 |
x1 |
Таким образом, b12 = 0,720; a11 = 8,722.
Найдем x1 из первого уравнения приведенной формы модели
|
x1 = |
(y1 - |
1,561 |
x2 ) / |
9,518 |
Подставим это выражение во второе уравнение приведенной модели, найдем структурное уравнение
|
y2= |
1,106 |
(y1 - |
1,561 |
x2 ) / |
9,518 |
+ |
2,168 |
x2 |
= |
|
= |
0,1162 |
y1 |
-0,18147 |
x2 |
+ |
2,168 |
x2 |
= |
|
= |
0,1162 |
y1 |
+ |
1,987 |
x2 |
Таким образом, b21 = 0,116; a22 = 1,987.
Свободные члены структурной формы находим из уравнений
А01= y1,cp - b12 y2,cp - a11 x1,cp = 91.167-0.720*41.583-8.722*6.333=5.988
А02= y2,cp - b21 y1,cp - a22 x2,cp = 41.583-0.116*91.167-1.987*9.167=12,773
Окончательный вид структурной модели
|
y1= a01+ b12 y2 + a11 x1 + e1= |
5,988 |
+ |
0,720 |
y2 |
+ |
8,722 |
x1 + e1 |
|
y2= a02+ b21 y1 + a22 x2 + e2= |
12,773 |
+ |
0,116 |
y1 |
+ |
1,987 |
x2 + e2 |