Контрольная работа
Количественные методы финансового
менеджмента
К=3
Задание
1.
Взята ссуда на 10 лет в сумме 20 000+1 000К
(у.д.е.) под 20+К процентов годовых, начисляемых на непогашенный остаток.
Возвращать нужно равными суммами в конце каждого года (начисление процентов
совпадает со временем возврата). Требуется: составить модель погашения
ссуды; вычислить величину годового
платежа; определить величину всей возвращаемой суммы и величину общей суммы
процентного платежа; сравнить данный вариант с вариантом возврата ссуды вместе
с процентами в конце срока операции.
Решение.
PV = 23 000 (у.д.е.), n = 10
r = 23 % годовых
Данная ссуда называется ипотечной. Обозначим CF (у.д.е.) величину годового платежа.
1) Модель погашения ссуды будет следующей:
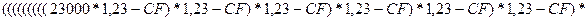
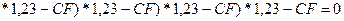

2) Решая это уравнение,
вычислим величину (сумму в у.д.е.) годового платежа:
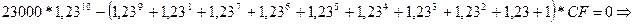
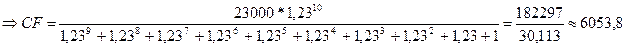
Применяя
формулу
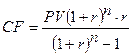 , получаем:
, получаем:
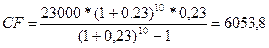
3) Общая сумма
процентного платежа в (у.д.е.) составит:
6 053,8 * 10 –
23 000 = 37 538
4) По второму варианту, при возврате в конце срока операции по окончании n периодов (лет), возвратная сумма 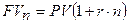 , а
процентный платеж составит
, а
процентный платеж составит 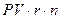 .
.
В данном случае 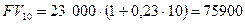 (у.д.е.) против 60 538 (у.д.е.) по первому
варианту, а общая сумма процентных платежей составит 52 900 (у.д.е.) против 37 538 (у.д.е.) по первому
варианту, т.е. первый вариант предпочтительнее второго.
(у.д.е.) против 60 538 (у.д.е.) по первому
варианту, а общая сумма процентных платежей составит 52 900 (у.д.е.) против 37 538 (у.д.е.) по первому
варианту, т.е. первый вариант предпочтительнее второго.
Задание 2.
Определить
будущую стоимость обыкновенного аннуитета накопления с реальной доходностью 20 процентов в год с учетом инфляции
(ежегодный темп инфляции составляет 10+К процентов), если ежегодный вклад
пренумерандо 1 200+100К (у.д.е.), а срок операции 7 лет.
Указание. Наращение производить по номинальной
процентной ставке, исчисленной по формуле Фишера.
Решение.
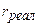 = 20 % ;
= 20 % ;  = 13 %
; CF = 1500
(у.д.е.), n = 7
= 13 %
; CF = 1500
(у.д.е.), n = 7
Номинальная ставка 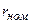 вычисляется по формуле:
вычисляется по формуле:
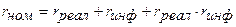 .
.
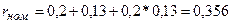
В общем виде модель
обыкновенного аннуитета пренумерандо имеет вид: 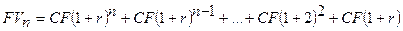 .
.
Применив
формулу для вычисления суммы геометрической прогрессии, получим: 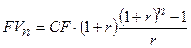 .
.
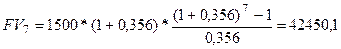
Задание 3.
Финансовый
инструмент (актив) генерирует ежегодно постнумерандо в течение 5 лет постоянную
сумму CF=2 000+100К (у.д.е).
Реальная
(приемлемая) доходность 10 процентов в год, ежегодный коэффициент риска rриска=0,05+0,01К.
Определить номинальную (необходимую) ежегодную ставку дисконтирования с учетом
фактора риска и современную (приведенную) стоимость данного аннуитета.
Решение.
СF = 2300; 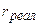 = 10 % ;
= 10 % ; 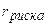 = 8 % ; n = 5
= 8 % ; n = 5
1) Номинальная
ставка 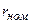 вычисляется по
формуле:
вычисляется по
формуле:
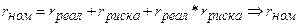 =
0,1+0,08+0,1*0,08 = 0,188
=
0,1+0,08+0,1*0,08 = 0,188
2) Так, как CF – постоянная величина, то современная стоимость обыкновенного
аннуитета вычисляется по формуле:
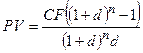 ; где
; где 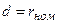 .
.
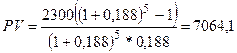
Задание 4.
Предприятие рассматривает
инвестиционный проект, первоначальные инвестиции по которому I0=15 000+1 000k (у.д.е). Ожидается, что реализация
проекта в течение 5 лет обеспечит получение чистого дохода по годам
постумерандо в объемах (у.д.е.): CF1=6 000+200К, CF2=8 000+200K, CF3=11 000+200К, CF4=10 000+200К, CF5=7 000+200К. Принятая ежегодная норма (ставка)
дисконта d=10+k процентов постоянна в течение всех лет экономической жизни проекта.
Требуется: 1) оценить экономическую эффективность проекта, вычислив NPV, PI; 2) сравнить данный проект с
альтернативным у которого Ia=25 000+1 000К, NPVa=6 000+250К, а срок экономической
жизни тоже 5 лет.
Решение.
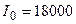 ; n = 5; d = 13 %
; n = 5; d = 13 %
Используя формулы
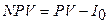 ;
;
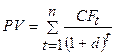 ;
;
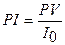 .
.
вычислим PV, NPV, PI, результаты вносим в таблицу
(вычисления произведены с точностью до целых по потокам, а по коэффициентам до
четвертого знака).
|
t
|
CFt (у.д.е.)
|
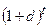
|
PVt (у.д.е.)
|
NPVt (у.д.е.)
|
|
0
|
- 18 000
|
|
1
|
6 600
|
1,131 = 1,1300
|
6 600 / 1,13 = 5 841
|
- 12 159
|
|
2
|
8 600
|
1,132 = 1,2769
|
8 600 / 1,2769 = 6 735
|
- 5 424
|
|
3
|
11 600
|
1,133 = 1,4429
|
11 600 / 1,4429 = 8
039
|
2 615
|
|
4
|
10 600
|
1,134 = 1,6305
|
10 600 / 1,6305 = 6
501
|
9 116
|
|
5
|
7 600
|
1,135 = 1,8424
|
7 600 / 1,8424 = 4 125
|
13 241
|
|
Итого 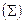
|
45 000
|
|
31 241
|
NPV = 13 241
|
В последней колонке таблицы при
вычислении NPVt дисконтированные суммы поступлений по годам складывались с
суммой долга (затратами), результат NPV = 31 241 – 18 000 = 13 241 (у.д.е.).
NPV>0 свидетельствует о том, что затраты при требуемой
доходности возмещены. Полученная чистая приведенная (современная) стоимость
(доход) 13 241 (у.д.е.) позволяет считать проект
экономически эффективным по методу NPV.
Индекс (коэффициент) рентабельности
данного проекта 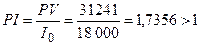 подтверждает
рентабельность проекта. Коэффициент доходности за весь период
подтверждает
рентабельность проекта. Коэффициент доходности за весь период 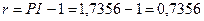
2) 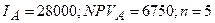
Для сравнения
данного проекта с альтернативным вычислим для альтернативного индекс
рентабельности 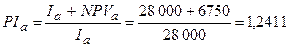 .
.
Альтернативный проект тоже
рентабелен, но данный проект более рентабелен (особенно в случае ограниченности
средств). Действительно, при таком же сроке экономической жизни данный проект
требует меньше первоначальных инвестиций (18 000 < 28 000), а
рентабельность его выше, чем альтернативного (1,7356 > 1,2411). Таким
образом, первый проект является более предпочтительным.
Задание 5
Корпорации предлагается
сформировать инвестиционную программу из шести проектов на четыре года при
условии, что инвестиционные затраты по годам превышают установленный лимит
средств (возможности корпорации по инвестированию ограничены). Корпорация имеет
высокий финансовый рычаг и не планирует привлекать заемные средства.
Рассматриваемые шесть проектов независимы и имеют тот же класс (уровень) риска,
что и текущая деятельность корпорации. Проекты реализуются в объеме не более
одного раза, а при необходимости могут реализоваться (инвестироваться)
частично, при этом эффект, выраженный NPV, пропорционален доле реализации
каждого проекта.
Требуется: составить
экономико-математическую модель задачи максимизирующей суммарный NPV
Решение.
Данные по затратам
(инвестированию проектов по годам), лимит капитала bi и NPVj приведены в таблице:
Годы
|
Инвестиционные затраты по проектам (у.д.е.)
|
Лимит капитала (bi) по годам (у.д.е.)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
230
|
30
|
240
|
140
|
90
|
70
|
550
|
|
2
|
250
|
230
|
130
|
180
|
70
|
90
|
600
|
|
3
|
30
|
90
|
80
|
30
|
80
|
330
|
450
|
|
4
|
60
|
70
|
30
|
70
|
230
|
30
|
350
|
|
NPVj
|
160
|
210
|
270
|
140
|
160
|
180
|
|
Экономико-математическая модель
задачи имеет следующий вид:
230x1 + 30x2 + 240x3
+ 140x4 + 90x5 + 70x6 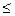 550
550
250x1 + 230x2 + 130x3
+ 180x4 + 70x5 + 90x6 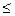 600
600
30x1
+ 90x2 +
80x3 +
30x4 + 80x5 + 330x6 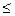 450
450
60x1
+ 70x2 +
30x3 +
70x4 + 230x5 +30x6
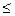 350
350
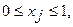
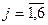
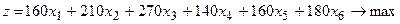 , где
, где 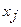 –доля реализации. j-го
проекта, ограничения отражают лимитирование ресурсов (инвестиционные
возможности корпорации по годам ограничены сверху),
–доля реализации. j-го
проекта, ограничения отражают лимитирование ресурсов (инвестиционные
возможности корпорации по годам ограничены сверху), 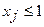 означает, что каждый
проект может быть реализован не более одного раза. Целевая функция модели
максимизирует оценку капитала (суммарный NPV) корпорации.
означает, что каждый
проект может быть реализован не более одного раза. Целевая функция модели
максимизирует оценку капитала (суммарный NPV) корпорации.
Задание 6
В
задачах 0-9 приведены модели, описывающие зависимость некоторого финансового
показателя от нескольких факторов. Требуется при помощи методов предельного
анализа: частной производной и коэффициента эластичности произвести анализ
чувствительности показателя на изменение факторов при конкретных значениях
факторов.
0. 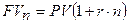 - модель наращения по
схеме простых процентов (1.1). Проанализировать изменение FVn при
изменении: 1) n – времени операции; 2) PV –
первоначальной суммы, если PV=100 (у.д.е.), r=0,2, n=5.
- модель наращения по
схеме простых процентов (1.1). Проанализировать изменение FVn при
изменении: 1) n – времени операции; 2) PV –
первоначальной суммы, если PV=100 (у.д.е.), r=0,2, n=5.
1. 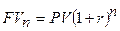 - модель
наращения по схеме сложных процентов (1.2). Проанализировать изменение FVn при
изменении: 1) r – коэффи-циента наращения; 2) PV –
первоначальной суммы, если PV=200 (у.д.е.), r=0,25, n=8.
- модель
наращения по схеме сложных процентов (1.2). Проанализировать изменение FVn при
изменении: 1) r – коэффи-циента наращения; 2) PV –
первоначальной суммы, если PV=200 (у.д.е.), r=0,25, n=8.
2. 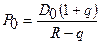 - модель
Гордона (4.6) стоимости (равновесной цены) бессрочной акции. Проанализировать
изменение P0 при изменении: 1) D0 –
дивидендов начального периода; 2) R – необходимого уровня доходности акции,
если D0=2, R=0,15, q=0,02.
- модель
Гордона (4.6) стоимости (равновесной цены) бессрочной акции. Проанализировать
изменение P0 при изменении: 1) D0 –
дивидендов начального периода; 2) R – необходимого уровня доходности акции,
если D0=2, R=0,15, q=0,02.
3. 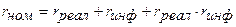 - модель
Фишера (1.19) зависимости номинальной ставки от реальной и инфляционной.
Проанализировать изменение rном при изменении: 1) rреал –
реальной ставки; 2) rинф – инфляционной ставки
(коэффициента инфляции), если rреал=0,4, rинф=0,15 в
год.
- модель
Фишера (1.19) зависимости номинальной ставки от реальной и инфляционной.
Проанализировать изменение rном при изменении: 1) rреал –
реальной ставки; 2) rинф – инфляционной ставки
(коэффициента инфляции), если rреал=0,4, rинф=0,15 в
год.
4. 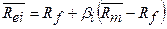 - модель
САРМ (4.6) оценки капитальных активов. Проанализировать изменение
- модель
САРМ (4.6) оценки капитальных активов. Проанализировать изменение 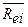 при изменении:1)
при изменении:1)  - β-коэффициента
активов
- β-коэффициента
активов 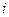 -й компании. 2)
-й компании. 2) 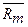 -
среднеожидаемой доходности рынка, если
-
среднеожидаемой доходности рынка, если 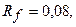
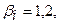
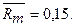
5. 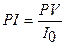 - модель
вычисления индекса рентабельности инвестиционного проекта (2.3).
Проанализировать изменение PI при изменении: 1) PV –
современной (приведенной) стоимости проекта; 2) I0 –
первоначальных инвестиционных затрат, если PV=7 000 (у.д.е.), I0=5 000
(у.д.е.).
- модель
вычисления индекса рентабельности инвестиционного проекта (2.3).
Проанализировать изменение PI при изменении: 1) PV –
современной (приведенной) стоимости проекта; 2) I0 –
первоначальных инвестиционных затрат, если PV=7 000 (у.д.е.), I0=5 000
(у.д.е.).
6. 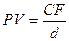 (1.17) – современная
(приведенная) стоимость бессрочного обыкновенного аннуитета постнумерандо.
Проанализировать изменение PV при изменении: 1) CF –
величины ежегодного денежного платежа;
(1.17) – современная
(приведенная) стоимость бессрочного обыкновенного аннуитета постнумерандо.
Проанализировать изменение PV при изменении: 1) CF –
величины ежегодного денежного платежа;
2) d –
нормы дисконтирования, если CF=1 200 (у.д.е.), d=0,15.
7. 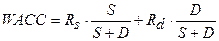 -
коэффициент доходности капитала компании, где Rs –
коэффициент доходности собственного капитала, Rd –
коэффициент доходности заемного капитала, S –
объем собственного капитала, D – объем заемного капитала. Проанализировать
изменение WACC при изменении: 1) S – объема (величины) собственного
капитала; 2) Rd – доходность заемного капитала, если S=100
(у.д.е.), D=300 (у.д.е.), Rs=0,15, Rd=0,10.
-
коэффициент доходности капитала компании, где Rs –
коэффициент доходности собственного капитала, Rd –
коэффициент доходности заемного капитала, S –
объем собственного капитала, D – объем заемного капитала. Проанализировать
изменение WACC при изменении: 1) S – объема (величины) собственного
капитала; 2) Rd – доходность заемного капитала, если S=100
(у.д.е.), D=300 (у.д.е.), Rs=0,15, Rd=0,10.
8. 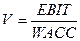 - объем
капитала компании, где EBIT – доналоговая прибыль (прибыль до уплаты налогов и
обязательств), WACC – средневзвешенная доходность капитала компании V.
Проанализировать изменение V при изменении: 1) EBIT; 2) WACC; если EBIT=100
000 (у.д.е), WACC=0,2.
- объем
капитала компании, где EBIT – доналоговая прибыль (прибыль до уплаты налогов и
обязательств), WACC – средневзвешенная доходность капитала компании V.
Проанализировать изменение V при изменении: 1) EBIT; 2) WACC; если EBIT=100
000 (у.д.е), WACC=0,2.
9. 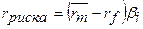 (1.25) – уровень премии за риск по
(1.25) – уровень премии за риск по 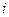 -му финансовому инструменту. Проанализировать изменение rриска при
изменении: 1)
-му финансовому инструменту. Проанализировать изменение rриска при
изменении: 1) 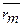 - средней нормы
доходности на финансовом рынке;
- средней нормы
доходности на финансовом рынке;
2)  - β-коэффициента
- β-коэффициента
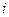 -го финансового инструмента, если
-го финансового инструмента, если 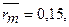
Решение.
0. 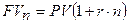 , PV=100 (у.д.е.), r=0,2, n=5.
, PV=100 (у.д.е.), r=0,2, n=5.
FVn = 100*(1+0.2*5) = 200 (у.д.е.)
1) При увеличении (уменьшении) количества периодов  на 1 будущая стоимость
увеличится (уменьшится) на величину
на 1 будущая стоимость
увеличится (уменьшится) на величину 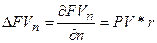 = 100 * 0,2 = 20 (у.д.е.)
= 100 * 0,2 = 20 (у.д.е.)
В данной модели посчитаем коэффициент частной эластичности по
фактору n:
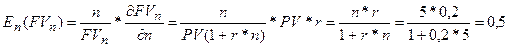
То есть, увеличение числа периодов на один пункт (процент) в
точке n=5, увеличивает будущую стоимость на 0,5 процента.
2) При увеличении настоящей стоимости 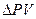 на 1 будущая стоимость
увеличится на величину
на 1 будущая стоимость
увеличится на величину 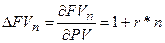 = 1+0,2 * 5 = 2 (у.д.е.)
= 1+0,2 * 5 = 2 (у.д.е.)
Посчитаем коэффициент частной эластичности по фактору PV:
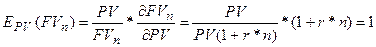
То есть, увеличение настоящей стоимости на один пункт
(процент) в точке PV =100 (у.д.е.) увеличивает будущую стоимость на 1 процент.
1. 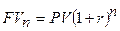 ; PV = 200 (у.д.е.), r = 0.25, n = 8
; PV = 200 (у.д.е.), r = 0.25, n = 8
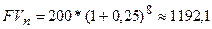 (у.д.е.)
(у.д.е.)
1)
При увеличении (уменьшении) процентной ставки 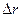 на 0,01 будущая
стоимость увеличится (уменьшится) на величину
на 0,01 будущая
стоимость увеличится (уменьшится) на величину 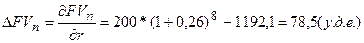
В данной модели посчитаем коэффициент частной эластичности по
фактору n:
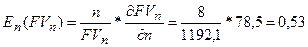
То есть, увеличение числа периодов на один пункт (процент) в
точке n=8, увеличивает будущую стоимость на 0,53 процента.
2) При увеличении настоящей стоимости 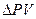 на 1 будущая стоимость
увеличится на величину
на 1 будущая стоимость
увеличится на величину 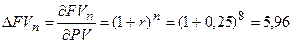 (у.д.е.)
(у.д.е.)
Посчитаем коэффициент частной эластичности по фактору PV:
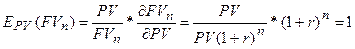
То есть, увеличение настоящей стоимости на один пункт
(процент) в точке PV = 200 (у.д.е.) увеличивает будущую стоимость на 1 процент.
2.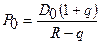 ; D0 = 2, R = 0,15, q = 0,02
; D0 = 2, R = 0,15, q = 0,02
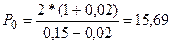 (у.д.е.)
(у.д.е.)
1) При увеличении (уменьшении) дивидендов начального периода ΔD0 на 1 равновесная
цена бессрочной акции увеличится (уменьшится) на величину 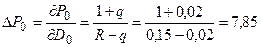 (у.д.е.)
(у.д.е.)
В данной модели посчитаем коэффициент частной эластичности по
фактору n:
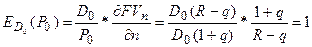
То есть, увеличение дивидендов на один пункт (процент) в
точке D0=2,
увеличивает равновесную цену бессрочной акции на 1 процент.
2) При увеличении (уменьшении) необходимого уровня доходности
акций на 0,01 равновесная цена
бессрочной акции увеличится (уменьшится) на величину 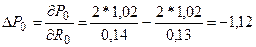 (у.д.е.)
(у.д.е.)
В данной модели посчитаем коэффициент частной эластичности по
фактору R:
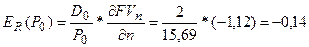
То есть, увеличение необходимого уровня доходности акций на
один пункт (процент) в точке R=0,15, уменьшает равновесную цену бессрочной акции на 0,14
процента.
3. 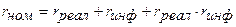 ;
;
rреал = 0,4, rинф = 0,15 в год.
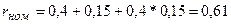 % в год.
% в год.
1) При увеличении реальной процентной ставки 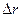 реал на 1 номинальная процентная ставка увеличится
на величину:
реал на 1 номинальная процентная ставка увеличится
на величину:
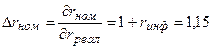
В данной модели посчитаем коэффициент частной эластичности по
фактору rреал:
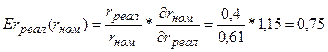
То есть, увеличение реальной процентной ставки на один пункт
(процент) в точке rреал=0,4 увеличивает номинальную процентную ставку на 0,75 процента.
2) При увеличении ставки инфляции 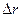 инф на 1 номинальная процентная ставка увеличится на
величину:
инф на 1 номинальная процентная ставка увеличится на
величину:
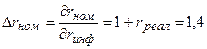
В данной модели посчитаем коэффициент частной эластичности по
фактору rинф:
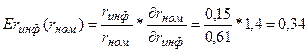
То есть, увеличение ставки инфляции на один пункт (процент) в
точке rинф=0,15
увеличивает номинальную процентную ставку на 0,34 процента.
4. 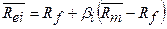 ; если
; если 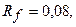
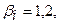
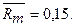
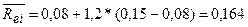
1) При увеличении 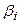 -
-  -коэффициента активов i-й компании на 0,01 -
-коэффициента активов i-й компании на 0,01 - 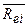 увеличится на
величину:
увеличится на
величину:
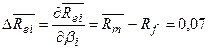
В данной модели посчитаем коэффициент частной эластичности по
фактору 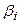 :
:
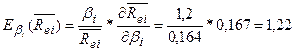
То есть, увеличение  -коэффициента активов i-й компании на один пункт (процент) в точке
-коэффициента активов i-й компании на один пункт (процент) в точке 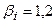 увеличивает
увеличивает 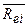 на 1,22 процента.
на 1,22 процента.
2) При увеличении 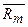 - среднеожидаемой доходности рынка на 0,01 -
- среднеожидаемой доходности рынка на 0,01 - 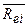 увеличится на
величину:
увеличится на
величину:
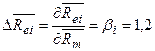
В данной модели посчитаем коэффициент частной эластичности по
фактору 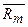 :
:
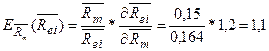
То есть, увеличение 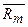 - среднеожидаемой доходности рынка на один пункт (процент) в точке
- среднеожидаемой доходности рынка на один пункт (процент) в точке 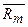 =0,15 увеличивает
=0,15 увеличивает 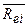 на 1,1 процента.
на 1,1 процента.
5. 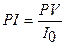 ; если PV=7 000 (у.д.е.), I0=5 000
(у.д.е.).
; если PV=7 000 (у.д.е.), I0=5 000
(у.д.е.).
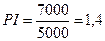
1) При увеличении PV- приведенной стоимости проекта на 1 (у.д.е.) индекс
рентабельности PI увеличится
на величину:
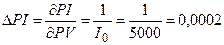 %
%
В данной модели посчитаем коэффициент частной эластичности по
фактору PV:
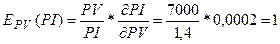
То есть, увеличение приведенной стоимости проекта PV на один пункт (процент) в точке PV=7000 увеличивает индекс рентабельности
проекта на 1 процент.
2) При увеличении первоначальных инвестиционных затрат I0 на 1 (у.д.е.) индекс рентабельности PI снизится на величину:
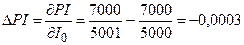 %
%
В данной модели посчитаем коэффициент частной эластичности по
фактору I0:
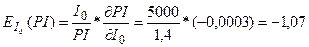
То есть, увеличение первоначальных инвестиционных затрат
проекта I0 на один
пункт (процент) в точке I0 = 5000 снижает индекс рентабельности проекта на 1,07 процента.
6. 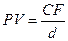 ; если СF = 1 200 (у.д.е.), d=0,15
(у.д.е.).
; если СF = 1 200 (у.д.е.), d=0,15
(у.д.е.).
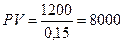 (у.д.е.)
(у.д.е.)
1) При увеличении СF - величины ежегодного денежного платежа на 1 (у.д.е.)
приведенная стоимость бессрочного обыкновенного аннуитета постнумерандо
увеличится на величину:
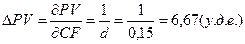
В данной модели посчитаем коэффициент частной эластичности по
фактору CF:
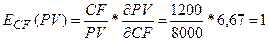
То есть, увеличение СF- величины ежегодного денежного
платежа на один пункт (процент) в точке CF=1200 (у.д.е.) увеличивает приведенную стоимость бессрочного
обыкновенного аннуитета постнумерандо на
1 процент.
2) При увеличении нормы дисконтирования d на 1% приведенная стоимость
бессрочного обыкновенного аннуитета постнумерандо снизится на величину:
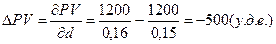
В данной модели посчитаем коэффициент частной эластичности по
фактору d:
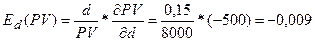
То есть, увеличение нормы дисконтирования на один пункт
(процент) в точке d=0,15 снизит приведенную стоимость бессрочного обыкновенного аннуитета
постнумерандо на 0,009 процента.
7. 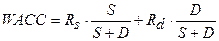
S=100 (у.д.е.), D=300 (у.д.е.), Rs=0,15,
Rd=0,10.
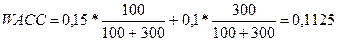
1) При увеличении S – величины собственного капитала на 1 (у.д.е.) коэффициент
доходности капитала WACC увеличится на величину:
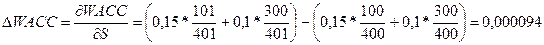
В данной модели посчитаем коэффициент частной эластичности по
фактору S:
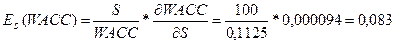
То есть, увеличение S – величины собственного капитала на один пункт (процент) в
точке S=100 увеличит WACC - коэффициент доходности капитала на 0,083 процента.
2) При увеличении Rd – доходности заемного капитала на 1 коэффициент
доходности капитала WACC увеличится на величину:
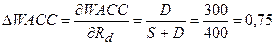
В данной модели посчитаем коэффициент частной эластичности по
фактору Rd:
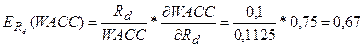
То есть, увеличение Rd – доходности заемного капитала на
один пункт (процент) увеличит WACC - коэффициент доходности капитала на 0,67 процента.
8. 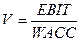 ; EBIT=100 000
(у.д.е), WACC=0,2.
; EBIT=100 000
(у.д.е), WACC=0,2.
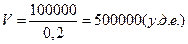
1) При увеличении EBIT – доналоговой прибыли на 1 (у.д.е.) объем капитала компании
увеличится на величину:
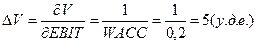
В данной модели посчитаем коэффициент частной эластичности по
фактору EBIT:
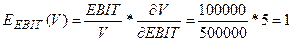
То есть, увеличение EBIT - величины доналоговой прибыли на один пункт (процент) в
точке EBIT = 100 000 (у.д.е.) увеличивает объем капитала компании на 1 процент.
2) При увеличении средневзвешенной доходности капитала
компании на 1% объем капитала компании снизится на величину:
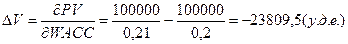
В данной модели посчитаем коэффициент частной эластичности по
фактору WACC:
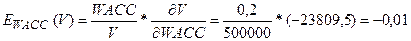
То есть, увеличение средневзвешенной доходности капитала на
один пункт (процент) в точке WACC=0,2 снизит объем капитала компании на 0,01
процента.
9. 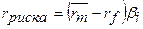 ;
; 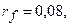
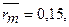
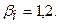
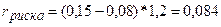
1) При увеличении  - средней нормы доходности на финансовом рынке на 1% уровень
премии за риск увеличится на величину:
- средней нормы доходности на финансовом рынке на 1% уровень
премии за риск увеличится на величину:

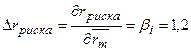
В данной модели посчитаем коэффициент частной эластичности по
фактору  :
:
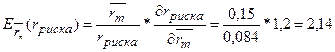
То есть, увеличение  - средней нормы доходности на финансовом рынке на один пункт
(процент) в точке
- средней нормы доходности на финансовом рынке на один пункт
(процент) в точке  =0,15 увеличивает
уровень премии за риск на 2,14 процента.
=0,15 увеличивает
уровень премии за риск на 2,14 процента.
2) При увеличении 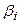 -
-  -коэффициента i-го финансового инструмента на 1 уровень премии за риск
увеличится на величину:
-коэффициента i-го финансового инструмента на 1 уровень премии за риск
увеличится на величину:

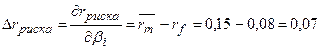
В данной модели посчитаем коэффициент частной эластичности по
фактору 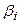 :
:
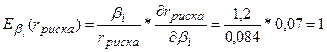
То есть, увеличение 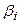 -
- -коэффициента i-го финансового инструмента на один пункт (процент) в точке
-коэффициента i-го финансового инструмента на один пункт (процент) в точке 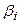 =1,2 увеличивает
уровень премии за риск на 1 процент.
=1,2 увеличивает
уровень премии за риск на 1 процент.
Задание 7.
Используя модель САРМ и формулу расчета стоимости
(цены) акции компании 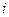 , произвести вычисления
, произвести вычисления 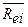 и
и 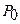 , а также
, а также 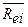 ' и
' и 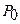 ' по следующим данным:
' по следующим данным:
|
Первоначальные
значения
|
Новые
значения
|
|
Номер
варианта
|
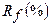
|
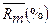
|

|
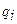
|
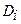
|
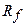 '(%) '(%)
|
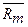 '(%) '(%)
|
 ' '
|
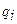 ' '
|
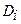 ' '
|
|
3
|
7
|
13
|
1,3
|
0,04
|
4
|
6
|
12
|
1,1
|
0,03
|
4
|
Построить график модели рынка по первоначальным значениям,
определить премии за риски.
Решение.
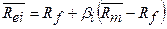
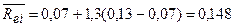 =14,8%
=14,8%
Рыночная премия за риск = 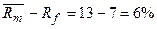
Премия за повышенный риск вложения в активы компании i по сравнению:
·
со
среднерыночным = 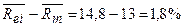
·
с
вложением в государственные ценные бумаги = 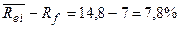
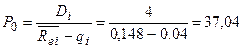

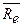 , %
, %



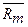 =13
=13
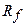 =7
=7
0 1 
Новые значения.
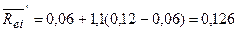 =12,6%
=12,6%
Рыночная премия за риск = 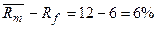
Премия за повышенный риск вложения в активы компании i по сравнению:
·
со
среднерыночным = 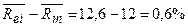
·
с
вложением в государственные ценные бумаги = 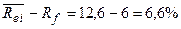
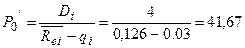
Задание 8.
На эффективном рынке известны доходность безрисковых активов 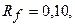 доходность рыночного
портфеля (рынка)
доходность рыночного
портфеля (рынка) 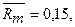 β-коэффициенты
β-коэффициенты
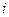 активов доступных для
выбора на рынке:
активов доступных для
выбора на рынке: 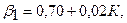
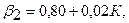
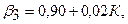
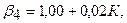
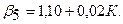 Кроме того, известно
предельное (сверху) значение β-коэффициента портфеля активов
Кроме того, известно
предельное (сверху) значение β-коэффициента портфеля активов 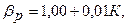 определенное
инвестором, желающим иметь портфель максимальной доходности (выделяемые
инвестором средства должны быть полностью инвестированы). Заданы дополнительно
следующие условия: доля первого актива в портфеле должна быть не менее
0,20+0,01К; сумма долей второго и третьего активов должна быть равна
0,30+0,01К; доля четвертого актива не должна превышать 0,50+0,01К, а доля
пятого актива не должна превышать 0,10+0,01К. Требуется: 1) рассчитать по
модели САРМ ожидаемые доходности всех пяти активов; 2) построить
экономико-математическую модель задачи, максимизирующей доходность портфеля,
сформированного из данных активов при заданных ограничениях.
определенное
инвестором, желающим иметь портфель максимальной доходности (выделяемые
инвестором средства должны быть полностью инвестированы). Заданы дополнительно
следующие условия: доля первого актива в портфеле должна быть не менее
0,20+0,01К; сумма долей второго и третьего активов должна быть равна
0,30+0,01К; доля четвертого актива не должна превышать 0,50+0,01К, а доля
пятого актива не должна превышать 0,10+0,01К. Требуется: 1) рассчитать по
модели САРМ ожидаемые доходности всех пяти активов; 2) построить
экономико-математическую модель задачи, максимизирующей доходность портфеля,
сформированного из данных активов при заданных ограничениях.
Решение.
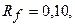
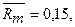
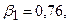

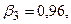
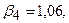
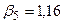 ,
,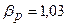
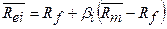
1) 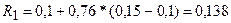 ;
;
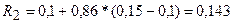 ;
;
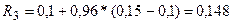 ;
;
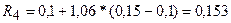 ;
;
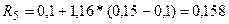 .
.
2) Экономико-математическая модель, максимизирующая
доходность портфеля имеет вид:

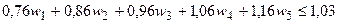
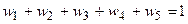
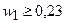
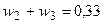
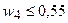
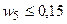
где 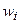 - веса актива I (
- веса актива I (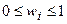 ).
).
Задание
9.
Предположим, что денежные расходы компании в
течение года составляют V=250 000+10 000К (у.д.е.); приемлемый и возможный для компании процентный
доход по краткосрочным ликвидным ценным бумагам r=0,07+0,01К, расходы по конвертации
(трансформированию) ценных бумаг в денежные средства с=70+10К (у.д.е).
Рассчитать, пользуясь моделью Баумоля – Тобина, сумму разового пополнения Q*, количество сделок по конвертации в год, общие
расходы по реализации такой политики (ОР); прокомментировать политику
управления денежными средствами.
Решение.
V = 280 000 (у.д.е.), r = 0,1; c = 100
1) Сумма разового
пополнения (у.д.е).
(у.д.е).
2) Средний объем денежных
средств на счете  (у.д.е.).
(у.д.е.).
3) Общее количество сделок
конвертации за этот период:
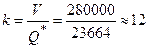
4) Общие расходы в течение
этого периода:
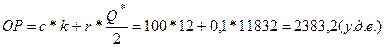
Таким образом, при истощении
денежных средств на расчетном счете компания должна конвертировать часть своих
ценных бумаг приближенно на сумму 23 664 (у.д.е). При равномерном расходовании
средств такая операция будет выполняться примерно один раз в месяц, при этом
оптимальный размер денежных средств должен колебаться на уровне около 22 664 (у.д.е.),
а средний около 11 832 (у.д.е). Общие расходы в течение этого периода составят
сумму 2383,2 (у.д.е.).
Задание 10.
Предположим, что определен минимальный ежедневный
остаток денежных средств компании в объеме Qн=500+100К
(у.д.е.), дисперсия ежедневных денежных потоков 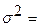 40 000+1 000К, процентная ставка (норма доходности по
высоколиквидным ценным бумагам) r=0,000 25+0,000 01К в день, расходы по конвертации
(операционные издержки по каждой покупке или продаже ценных бумаг) с=20+2К
(у.д.е). Рассчитать, пользуясь моделью Миллера – Орра, размах вариации R, верхний предел остатка
денежных средств QВ, точку возврата Q*, прокомментировать политику управления денежными
средствами компании.
40 000+1 000К, процентная ставка (норма доходности по
высоколиквидным ценным бумагам) r=0,000 25+0,000 01К в день, расходы по конвертации
(операционные издержки по каждой покупке или продаже ценных бумаг) с=20+2К
(у.д.е). Рассчитать, пользуясь моделью Миллера – Орра, размах вариации R, верхний предел остатка
денежных средств QВ, точку возврата Q*, прокомментировать политику управления денежными
средствами компании.
Решение.
Qн = 800 (у.д.е.); 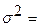 43 000; r = 0,00028; с = 26 (у.д.е.)
43 000; r = 0,00028; с = 26 (у.д.е.)
1)
Вычислим размах вариации 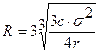 =
=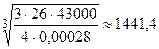 (у.д.е.),
(у.д.е.),
2)
Верхний предел 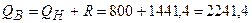 (у.д.е.).
(у.д.е.).
3)
Точка возврата 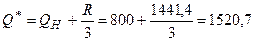 (у.д.е).
(у.д.е).
Если остаток денежных средств увеличивается до 2 241,4
(у.д.е.), то инвестируют 2241,4-1520,7=720,7 (у.д.е.) в ценные бумаги. Если же
остаток денежных средств уменьшается до 800 (у.д.е.), то продают ликвидные
ценные бумаги на сумму 720,7 (у.д.е.) и восстанавливают денежные средства в
нужном (оптимальном) объеме, т.е. постоянно возвращаются в точку возврата Q*=1520,7 (у.д.е.).