“Вестник ЦМО МГУ”, 1997 г., №1

Часть 3. “Математика, естественные и технические науки: методика и практика преподавания, теоретические и экспериментальные исследования”

 

МЕТОДИКА И ПРАКТИКА ПРЕПОДАВАНИЯ ЕСТЕСТВЕННО-НАУЧНЫХ

ДИСЦИПЛИН ИНОСТРАННЫМ УЧАЩИМСЯ

 

 510.6.005

 

МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ СИНТЕЗА ЛОГИЧЕСКИХ

ПРИЕМОВ МЫШЛЕНИЯ, ИСПОЛЬЗУЕМЫХ ПРИ

РАЗРАБОТКЕ СПОСОБОВ ДОКАЗАТЕЛЬСТВА

ТЕОРЕМ

 

Кузнецова Т.И.

(Центр международного образования МГУ им. М.В. Ломоносова)

 

1. Всякое знание об объекте всегда является результатом решения каких-то частных задач. Поэтому это знание представляет объект только с одной стороны, выделяет в нем одно или какую-то группу свойств, участвующих в решении определенной задачи. Решение новых задач, в которых участвует рассматриваемый объект, выделяет в нем новые свойства и соответственно образует новые знания.

Когда накоплено достаточно большое число таких, “односторонних” и частных, знаний, возникает особая теоретическая задача - объединить их в одном многостороннем знании об объекте. Решение этой задачи имеет не только теоретическое, но и практическое значение, так как оно позволяет рационализировать знания и тем самым ведет к экономии работы с ними.

Но как можно объединить в единой системе односторонние знания об объекте, полученные в связи с решением частных задач?

Нередко их объединяют чисто механически. При этом объект рассматривается как изоморфный той системе знания, которая может быть получена путем непосредственного объединения уже существующих, полученных независимо друг от друга частных знаний.

Конкретизируем нашу проблему на объекте, очень важном в математике - теореме. Теоремы занимают ведущее место как в школьном курсе математики, так и в целом ряде курсов высшей школы (высшая математика, физика, теоретическая механика и др.).

Процесс доказательства теорем анализировался в психолого-педагогических исследованиях (Ж. Адамар, И. Лакатос, Д. Пойа, Ю.М. Колягин, Л.М. Фридман, Г.А. Буткин, Н.Ф. Талызина и др.). Однако до последнего времени не был выявлен полный цикл знаний и умений, которые обеспечивают возможность самостоятельно разрабатывать способы доказательства теорем. Поэтому способы доказательства теорем до сих пор представляются обучаемым в готовом виде.

Усвоение способов доказательств теорем во всех областях, особенно в высшей математике, встречает серьезные трудности у обучаемых: они не запоминают их процедуры, часто не понимают смысла, не умеют применять на практике и поэтому, как правило, просто заучивают. В итоге не происходит усвоение материала, не развивается математическое мышление.

Таким образом, до последнего времени не было выработано положений для планомерной разработки способов доказательства теорем. Каждый способ когда-то был предметом специального открытия. При этом общие пути их создания оставались неизвестными. Набор способов доказательств теорем представлял собой чисто механическое объединение.

 

2. Подход к проблеме синтеза знаний, относимых к одному объекту, может быть совершенно иным, отличным от механического, так как абстракции не всегда выделяют части изучаемого объекта - они образуются иначе. Содержание знаний, получаемых при решении частных задач, можно сравнить с проекциями, которые “снимаются” с объекта при разных его “поворотах” [1].

Проиллюстрируем понимаемое таким образом отношение между несколькими знаниями и объектом, который мы изучаем. Изобразим объект и знания (А), (В), (С), фиксирующие разные “стороны” объекта, кругами. Тогда проекции кругов (А), (В), (С) на круг объекта будут символизировать “объективное содержание”, которое выделяется и фиксируется знаниями (А), (В), (С).

 

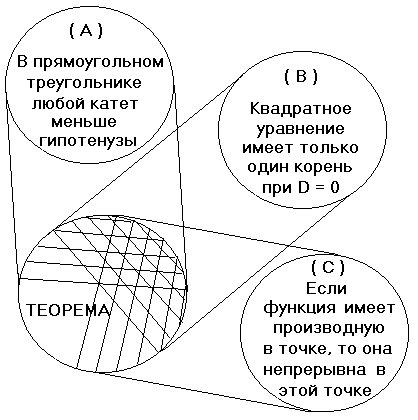
Рис.1

 

Если взять рассматриваемый нами объект - теорему как общенаучное понятие, то круги (А), (В), (С) могут символизировать какие-то знания о теореме, например, формулировки конкретных теорем (см. рис.1).

Ясно, что чисто механическое объединение таких проекций не может дать представления о действительном строении объекта. Попытки такого объединения с последующей формальной объективизацией полученной таким образом системы знаний так же бесперспективны, как и попытки получить представление о структуре детали путем простого присоединения друг к другу ее чертежных проекций. Но каким же образом осуществить синтез различных односторонних знаний об одном объекте? В этом и заключается наша проблема.

 

3. Обоснованный методологический подход к этой проблеме требует прежде всего четкого и резкого разграничения понятий объекта и предмета изучения. В контексте рефлексивного методологического исследования естественно рассматривать противопоставление объекта и знаний о нем как нечто реально существующее и весьма существенное для многих процедур и приемов научного и философского мышления. Понятие предмета изучения строится именно на этом отношении между объектом и знаниями о нем. Cчитается, что, если объект независим от исследования и противостоит ему, то предмет изучения, напротив, формируется самим исследователем. Это - конструкция, созданная мышлением или наукой, существующая лишь постольку, поскольку есть знания об объекте. Исследователь, приступая к изучению какого-либо объекта, берет его с одной или нескольких сторон; выделенные и зафиксированные в знании стороны объекта становятся “заместителем” всего объекта в целом. Таким образом, предмет исследования рассматривается как результат и продукт деятельности, как продукт человеческого мышления, не тождественный объекту и не сводимый к нему, существующий в особых средствах науки и, как особое создание человеческого общества, подчиняющийся особым закономерностям, не совпадающим с закономерностями самого объекта.

При этом характер предмета зависит не только от того, какой объект он отражает, но и от того, зачем этот предмет сформирован, для решения какой задачи. Итак, объект и задачи исследования являются теми двумя факторами, которые определяют, как и с помощью каких средств - приемов и способов исследования - будет сформирован необходимый для решения поставленной задачи предмет.

Конкретизируем исследование нашего объекта - теоремы на решении следующей задачи - обеспечить возможность самостоятельно разрабатывать способы доказательства теорем. Успешное решение этой задачи является одним из основных звеньев организации самостоятельной познавательной деятельности студентов. Объект и задача исследования определили предмет исследования - логические приемы мышления, которые лежат в основе самостоятельной разработки способов доказательства теорем. В работах И.П. Калошиной, Н.В. Миничкиной, Г.И. Харичевой выделяются два взаимосвязанных цикла логических приемов [2 - 6]:

- логических приемов, лежащих в основе разработки способов доказательства теорем в разных предметных областях;

- логических приемов, обеспечивающих разработку вариантов доказательства одной и той же теоремы.

Результатом решения поставленной задачи явилось выделение обобщенного состава действий по самостоятельной разработке способов доказательства теорем [6].

 

4. Что же позволило авторам решить такую сложную задачу: каким образом должен осуществляться синтез различных теоретических представлений и знаний, если они получены “хаотично”, вне связи друг с другом и без всякой ориентировки на последующий синтез. Ясно, что в такой ситуации первый шаг должен состоять в том, чтобы перестроить сами исходные представления и знания, освободить их от одинаковых повторяющихся элементов содержания, дополнить другими представлениями, которые окажутся необходимыми с точки зрения задачи синтеза.

Попытка проделать такое движение сразу же наталкивается на видимый парадокс: чтобы новые (полученные в результате перестройки) исходные представления увязывались с задачей синтеза, исследователь должен уже в исходном пункте иметь представление о действительной структуре объекта, который он изучает и хочет воспроизвести, и, кроме того, он должен соотнести с этим представлением все существующие односторонние проекции - знания. Иначе говоря, построение сложного, системного знания об объекте предполагает в качестве своего предварительного условия знание структуры этого объекта.

 

5. На первый взгляд кажется, что это требование содержит в себе противоречие. Но другого способа решить поставленную задачу нет, а более детальный анализ ситуации убеждает нас в том, что обнаруживаемое здесь противоречие - мнимое. Прежде всего потому, что искомое структурное представление объекта еще не есть теоретическое представление или теоретическое знание структуры этого объекта , оно лежит в особой плоскости представлений об объекте - методологической - и выполняет особую методологическую функцию в процессе исследования, являясь лишь средством для построения теоретического знания.

Такой вывод задает направление того движения, которое должно быть осуществлено для синтеза уже существующих знаний об объекте: он подчеркивает то, что нельзя получить решения этой проблемы, оставаясь в плоскости одних лишь имеющихся знаний. Он показывает, что в это движение обязательно должен войти анализ тех процедур, посредством которых были получены существующие знания. Он показывает также, что нужно проделать особую работу по воссозданию структуры того объекта, проекциями которого являются уже имеющиеся знания.

Идея такого движения в исследовании схематично изображена на рис.2. Знак К здесь обозначает новую знаковую форму, представляющую структуру объекта. Сплошные стрелки символизируют теоретико-методологическое движение по построению этой знаковой формы, исходя из уже существующих знаний (А), (В), (С), а штриховые стрелки - характеристику и объяснение этих знаний как “проекций” объекта (его нового представления К).

 

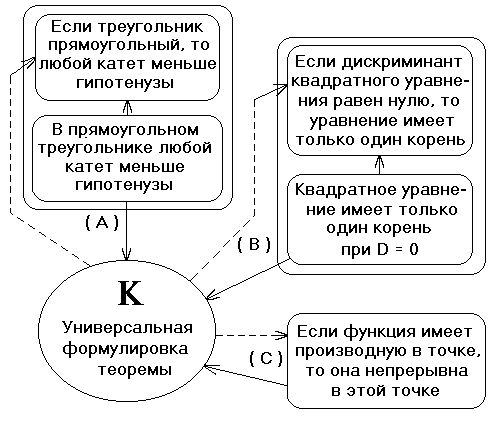
Рис.2

 

Cхема наглядно показывает, что, решая задачу синтеза различных знаний об одном объекте, нужно, вместо того, чтобы искать какие-то связи между ними в их собственной плоскости, воспроизвести каким-то образом структуру объекта, а затем, исходя из нее, восстановить те “проекции”, которые привели к имеющимся знаниям.

Проведенные рассуждения показывают, что процедуры анализа существующих знаний об объекте и их синтеза, полученные посредством абстрагирования представлений и знаний, должны быть органически связаны между собой, должны образовывать единый познавательный механизм. Этот принцип может быть применен к любым теоретическим знаниям и представлениям, которые мы хотим объединить.

Ценность работ И.П. Калошиной, Н.В. Миничкиной и Г.И. Харичевой заключается в том, что в них создано такое представление теоремы как общенаучного понятия, которое позволило рассматривать предмет исследования с целью решения поставленной задачи, т.е. с целью синтеза всех существующих способов доказательства теорем. Анализируя формулировки теорем, авторы обратили внимание на то, что в любой теореме условие и заключение связаны между собой либо условием необходимости, либо условием достаточности, либо условием необходимости и достаточности.

В результате было получено представление теоремы в виде ее универсальной формулировки: любая теорема в любой области знаний может быть представлена в одной из двух форм: “Если А, то В” или “Если А, то В, и наоборот, если В, то А”. В таком виде теоремы всегда выражают отношения необходимости (достаточности) - первый тип суждений, или необходимости и достаточности - второй тип суждений.

Например, в теореме “Если функция имеет производную в точке , то она непрерывна в этой точке” то, что функция имеет производную в точке , выступает достаточным условием для ее непрерывности в этой точке, а непрерывность функции в точке является необходимым условием для того, чтобы она имела производную в этой точке.

В схеме рис.2 для нашего конкретного случая фигуры (А), (В), (С) символизируют отдельные теоремы, К - новую универсальную формулировку теоремы, сплошные стрелки - анализ существующих формулировок теорем с точки зрения наличия в них условий необходимости и (или) достаточности, штриховые стрелки - процесс объяснения формулировок теорем как “проекций” универсальной формулировки. Последнее не всегда так просто, как в приведенном примере, где теорема уже сама имеет универсальную формулировку. В общем случае это требует переформулирования теорем. Так, теорему “В прямоугольном треугольнике любой катет меньше гипотенузы” необходимо представить в виде “если треугольник прямоугольный, то любой его катет меньше гипотенузы”.

 

6. После того, как специальное представление объекта (К) получено, начинается следующий этап мыслительной работы - использование представления уже непосредственно для синтеза знаний в единой теоретической системе.

Чтобы связать и действительно объединить знания, их нужно еще предварительно перестроить. Именно эта работа и осуществляется на втором этапе. Начинается новое, вторичное соотнесение уже существующих знаний с разработанным на их основе представлением объекта в свете специальной целевой установки: сделать их теоретически однородными и объединяемыми. Это всегда ведет к перестройке знаний, часто настолько существенной, что она выступает как процесс замены одних знаний другими. Этот процесс продолжается до тех пор, пока нам, наконец, не удается свести исходную совокупность знаний к единому сложному знанию, выводимому из имеющегося у нас представления объекта. При этом очень трудно ответить на вопрос, что же мы делаем “на самом деле” - объединяем исходные разрозненные знания, сводим их к новому целостному знанию или выводим это последнее из имеющегося представления объекта. Практически в большинстве случаев преобладает последнее.

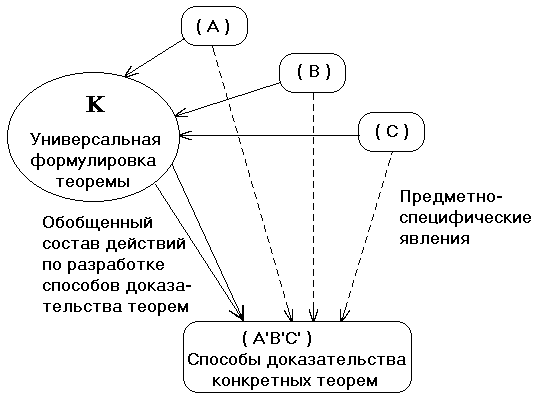
Рис.3

 

В наглядной форме такие отношения и функции представления объекта изображены на рис.3. Фигура (А’В’C’) символизирует систему перестроенных знаний, а двойная стрелка - процедуру получения этой системы на основе специального представления объекта (К). Все остальные элементы схемы совпадают с теми, которые были представлены на рис.2.

Такое объединение знаний имеет неоспоримую ценность: его итогом является своеобразное “сплющивание” всех знаний об объекте, расположенных как бы в разных планах и проекциях и потому непосредственно не сводимых одно к другому. Это “сплющивание” является непременным условием сложного знания об объекте. Такая организация, которая часто называется “линейной” или “плоскостной”, существенно облегчает оперирование системой знаний, и в частности, обеспечивает ее формализацию.

В нашем случае такой подход к решению поставленной задачи (путем создания универсальной формулировки теоремы) позволил выделить логические приемы мышления, лежащие в основе разработки способов доказательства теорем:

1) Анализ формулировки теоремы. Он заключается в том, чтобы по форме суждения, представляющего теорему, определить, каким условием (необходимости, достаточности или необходимости и достаточности) связаны между собой события, о которых в ней говорится.

2) Подведение предметно-специфических явлений, о которых говорится в теореме, под логические понятия “необходимое условие”, “достаточное условие”, “необходимое и достаточное условие”. Анализ структуры этого приема позволил выделить в качестве его составляющих три важнейших приема:

а) прием разработки логической схемы доказательства: установление того, какое событие в составе какого следует искать;

б) прием представления событий, о которых говорится в теореме, обобщенным символическим способом (в формулировке теоремы события обычно даются в вербальной форме), т.е. в виде обобщенных символических выражений, которые раскрывают природу событий и дают возможность преобразования на уровне символов в целях обнаружения одного события в составе другого;

в) прием получения из одного обобщенного события другого, связанного с первым логическими отношениями. Выделяются три способа перехода от одного события к другому. Первый состоит в переходе от одного события к другому путем выявления какого-либо одного или нескольких свойств первого события и установления их эквивалентности второму событию. Второй способ заключается в выявлении формул, взаимосвязывающих указанные события и их части. Третий способ направлен на то, чтобы показать, что оба события порознь эквивалентны третьему событию.

3) Установление эквивалентных определений логических понятий “необходимое условие”, “достаточное условие”, “необходимое и достаточное условие”. Объективное существование различных определений этих логических понятий объясняет существование разных способов доказательства теорем. Выделяются два способа получения таких определений: на основе использования

а) взаимообратной зависимости между необходимостью и достаточностью,

б) закона исключенного третьего.

 

Такое целенаправленное изучение предмета исследования позволяет нам перейти к непосредственному решению поставленной задачи - выделить цикл логических приемов, которые обеспечивают возможность самостоятельно разрабатывать способы доказательства теорем (назовем его обобщенным составом действий по разработке способов доказательства теорем):

 

I. Логический анализ формулировки теоремы в свете созданного представления:

1) установление логической формы суждения, представляющего теорему;

2) выделение в суждении двух событий, взаимосвязь которых утверждается в теореме;

3) установление по форме суждения логического характера взаимосвязи между этими событиями;

4) вывод о том, какой характер логических отношений - необходимый, достаточный, необходимый и достаточный - требуется доказать.

 

II. Разработка логических схем доказательства отношений необходимости, достаточности, необходимости и достаточности между двумя событиями:

1) воспроизведение канонических определений логических понятий “необходимое условие”, “достаточное условие”, “необходимое и достаточное условие”;

2) создание различных вариантов эквивалентных определений этих отношений на основе использования:

а) взаимообратной зависимости между необходимостью и достаточностью;

б) закона исключенного третьего;

3) построение логических схем доказательства отношений необходимости, достаточности, необходимости и достаточности, устанавливающих, какое событие в составе какого надо искать, на основе структуры эквивалентных определений этих отношений.

 

III. Разработка программы реализации схем доказательства на основе приемов обобщенного представления событий и преобразования одного события в другое:

1) выражение обобщенным символическим способом событий, о которых говорится в формулировке теоремы;

2) установление обобщенных способов получения из одного события другого.

 

IV. Выполнение доказательства теоремы:

1) выбор одной из схем доказательства, определяющих, какое событие в составе какого надо искать;

2) выбор способа обобщенного символического представления событий, о которых говорится в теореме, и его реализация;

3) выбор одного из разработанных путей для получения из одного события другого и его реализация;

4) вывод о том, можно ли разработанным способом осуществить доказательство теоремы. Если нельзя, выбор другого способа и его реализация;

5) заключение о том, действительно ли события, представленные в теореме, связаны отношениями необходимости, достаточности, необходимости и достаточности.

В схеме рис.3 фигура (А’В’С’) символизирует разработанные способы доказательства теорем, двойная стрелка - обобщенный состав действий по разработке способов доказательства теорем, штриховые стрелки - предметно-специфические явления, описываемые в каждой конкретной теореме. Отметим, что обобщенный состав действий позволяет разрабатывать только логические схемы доказательства: для осуществления доказательств конкретных теорем необходимо хорошее владение предметно-специфическими знаниями и умениями из одной или нескольких областей знания.

 

7. Подводя итог изложенному, определим значение введенного представления объекта (K), охарактеризовав его функции и природу:

1) оно собрало и объединило в себе все то объективное содержание, которое было зафиксировано в уже имеющихся ранее знаниях;

2) его структура была введена как “основание” и “источник” всех проявлений объекта, обнаруживаемых в прямом познавательном оперировании с этим объектом;

3) на основе особого познавательного оперирования с самим этим представлением и выраженным в нем предметом знания выводились и обосновывались новые сложные знания об объекте.

Все эти моменты: сначала - особое назначение этого представления, затем - специфика процедур его создания и, наконец, - специфика его употребления, задают ему совершенно особое место в системе научного предмета.

Так как именно из этого представления выводятся потом все уже существующие знания об объекте, и оно либо служит их основанием, либо заставляет их перестраивать, поскольку именно на его основе строится новое синтетическое знание, которое затем используется в практической работе, постольку это представление является моделью объекта.

Поскольку эта модель объекта создается с совершенно особым назначением - специально для того, чтобы объединить уже существующие знания, она имеет специфический набор функций и совершенно особые характеристики формы и содержания, которые должны быть особым образом обозначены. В методологии такое представление объекта, создаваемое с целью описанного выше объединения и синтеза разных знаний, называют “конфигуратором”, а процедуру этого объединения и синтеза, основывающуюся на специально созданном для этого представлении объекта, - “конфигурированием”.

Таким образом, мы рассмотрели пример модели-конфигуратора - универсальной формулировки теоремы, которая позволила осуществить конфигурирование знаний по разработке различных способов доказательства теорем. Это один из примеров практического применения научного метода восхождения от абстрактного к конкретному.

 

8. Теперь обратимся к конкретному примеру применения обобщенного состава действий для разработки способов доказательства теоремы:

 

“Если функцию можно представить в виде суммы числа и некоторой бесконечно малой функции (при ), то число является пределом функции (при ).

Обратно, если функция имеет предел (при ) , то ее можно представить как сумму числа и бесконечно малой функции (при ) .

Выполняем первую группу действий. Согласно первому пункту устанавливаем, что данная теорема представлена двумя условными суждениями типа “Если..., то...”.

В соответствии со вторым пунктом выделяем два события, взаимосвязь которых утверждается в теореме: A - “функцию можно представить в виде суммы числа и некоторой бесконечно малой функции (при )” и B - “предел функции при равен ”.

В третьем пункте устанавливаем, что выделенные события А и В связаны между собой отношением необходимости и достаточности.

Реализуя четвертый пункт, делаем вывод, что в данной теореме утверждается отношение необходимости и достаточности между выделенными событиями.

Выполняем вторую группу действий. В соответствии с первым пунктом воспроизводим “каноническое” определение понятия “необходимое и достаточное условие”[4]: “ некоторое событие В называется необходимым и достаточным условием для события А, если оно 1) встречается при всех проявлениях события А и 2) не встречается ни при одном проявлении события не-А”.

Согласно второму пункту обращаемся к эквивалентным определениям понятия “необходимое и достаточное условие”, составленным на основе использования взаимообратной зависимости между необходимостью и достаточностью и закона исключенного третьего [6, c. 79-80, c. 82].

В соответствии с третьим пунктом строим возможные логические схемы доказательства отношения необходимости и достаточности [6, c.85-86]:

 

Схема 1. Сначала некоторым обобщенным способом надо показать наличие события В у всех проявлений события А, а затем подобным способом показать наличие события не-В у всех проявлений события не-А.

 

Схема 2. Сначала необходимо некоторым обобщенным способом показать наличие события А у всех проявлений события В, а затем - наличие события не-А у всех проявлений события не-В.

 

Схема 3. Сначала некоторым обобщенным способом нужно показать наличие события В у всех проявлений события А, а затем - наличие события А у всех проявлений события В.

 

Схема 4. Сначала некоторым обобщенным способом надо показать наличие события не-В у всех проявлений события не-А, а затем - наличие события не-А у всех проявлений события не-В.

 

После этого приступаем к выполнению третьей группы действий. Осуществляя первый пункт, устанавливаем, что в формулировке теоремы оба события выражены в обобщенной вербальной форме и поэтому должны быть выражены обобщенным символическим способом. Вспоминаем или находим в учебнике соответствующие выражения событий, о которых говорится в формулировке теоремы. Событие А: , ; событие В: при .

Выполняя второй пункт, устанавливаем обобщенные способы получения из одного события другого. В данном случае выбирается первый способ, который состоит в применении операций, в частности, математических, для перехода от одной формы обобщенного выражения преобразуемого события к другой.

Наконец, приступаем к реализации четвертой группы действий. В соответствии с первым пунктом выбираем одну из разработанных логических схем доказательства необходимости и достаточности, например, третью.

Исходя из второго пункта, выбираем способы обобщенного выражения явлений, представленных в формулировке теоремы. Событие А: , ; cобытие В: .

Согласно третьему действию получаем: , где . Отсюда , или . Последнее выражение совпадает с обобщенным выражением события В. И, наоборот, из выражения получаем , что означает, что a - бесконечно малая, т. е. получено событие А.

В соответствии с четвертым пунктом делаем вывод, что указанным способом можно доказать данную теорему, более того, что она уже доказана.

Выполняя пятый пункт, приходим к заключению, что события, представленные в данной теореме, действительно связаны отношением необходимости и достаточности.

 

9. Применительно к практике обучения доказательству теорем можно сделать следующие выводы:

1) Выделенные логические приемы мышления являются компонентами творческой деятельности.

2) Эти логические приемы необходимо ввести в содержание образования - в ту его часть, которая связана с передачей молодому поколению творческих знаний и умений.

3) Применение указанных логических приемов обеспечивает самостоятельную разработку обучаемыми способов доказательства теорем.

4) Рассмотренные логические приемы позволяют обучаемым создавать варианты способов доказательства одной и той же теоремы, применяя для этого разные эквивалентные определения логических понятий “необходимое условие”, “достаточное условие”, “необходимое и достаточное условие”.

5) Предложенный обобщенный состав действий по разработке способов доказательства теорем формирует у обучаемых умения разрабатывать способы доказательства теорем на основе логических приемов мышления.

6) Поскольку представленный состав действий позволяет разрабатывать только логические схемы доказательства теорем, и для осуществления доказательств конкретных теорем необходимо хорошее владение предметно-специфическими знаниями и умениями из одной или нескольких областей знания, то работа по этой схеме способствует естественной систематизации и в определенном плане алгоритмизации предметно-специфических знаний обучаемых.

 

 

 

Библиография

 

1. Щедровицкий Г.П. Синтез знаний: проблемы и методы. - В кн.: На пути к теории научного знания. М.: Наука, 1984, с. 67 - 109.

2. Калошина И.П. Структура и механизмы творческой деятельности.- М.: Изд-во Моск. ун-та, 1983. - 168 с.

3. Калошина И.П., Миничкина Н.В. Логические приемы мышления как условие самостоятельной разработки студентами способов доказательства теорем. - В кн.: Подготовка учителя математики в университете. Саранск, 1984, c.22 - 33.

4. Калошина И.П., Харичева Г.И. Логические приемы мышления при изучении высшей математики. - Воронеж: Изд-во Воронежского ун-та, 1978. - 128 с.

5. Демидов В.П., Калошина И.П., Миничкина Н.В. Как формировать у студентов творческое математическое мышление. - В кн.: Сборник научно-методических статей по математике. М.: Высшая школа, 1983.- 36 с.

6. Миничкина Н.В. Формирование логических приемов мышления как условия самостоятельной познавательной деятельности студентов. - Дис. ... канд. пед. наук. Саранск, 1984.-268 с.

 Е. Миганова, Г. Саранцев, г. Саранск

Красота математики

О красоте математики написано немало. Авторы видят ее в гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, в изяществе математических доказательств, в порядке, богатстве приложений, универсальности математических методов. Под понятие красоты подводится широкий спектр различных объектов от схем зверушек, составленных из отрезков, до представления красивого объекта моделью, удовлетворяющей требованиям изоморфизма1, простоты и неожиданности. Так, Э.Т. Белл привлекательность математического объекта видит в совокупности следующих характеристик:

— универсальность использования в различных разделах математики, как правило, изначально совсем неочевидная; — продуктивность или возможность побудительного влияния на дальнейшее продвижение в данной области на основе абстракции и обобщения; — максимальная емкость охвата объектов рассматриваемого типа [2].

Указанная совокупность признаков красивого математического объекта, как и другие предлагаемые наборы характеристик красоты, сформулирована не вполне четко и несколько размыто, что объясняется их «трудной уловимостью» и неполной осознаваемостью.

Наиболее четко характеристика эстетической привлекательности математического объекта дана Г. Биркгофом: M=O/C, где M — мера красоты объекта, O — мера порядка, а C — мера усилий, затрачиваемых для понимания сущности объекта [3]. С формулой красоты, предложенной Г. Биркгофом, созвучна модель, разработанная В.Г. Болтянским [4]. По его мнению, красота математического объекта может быть выражена посредством изоморфизма между этим объектом и его наглядной моделью, простотой модели и неожиданностью его появления. Изоморфизм предполагает правильные, неискаженные отражения основных свойств явления в его наглядной модели. Созвучность видится в том, что как в первой, так и во второй модели мера красоты тем выше, чем меньше мера сложности объекта (по Биркгофу) или чем проще наглядная модель исследуемого объекта (по Болтянскому).

Надо сказать, что проблема красоты занимает не только математиков, она привлекала и привлекает внимание величайших умов человечества. Одни исследователи считают, что в красоте объектов проявляется их свойство, существующее независимо от сознания. Чувство красоты трактуется как продукт отражения в человеческом сознании реально существующих эстетических свойств окружающего мира. Другие рассматривают красоту как продукт ума, свободной мысли. Для третьих красота является даром богов, особенно женская красота, воспеваемая в поэзии, литературе, живописи. Писатель-фантаст А. Казанцев во второй половине прошлого столетия выдвинул версию, согласно которой красивыми кажутся те черты лица, которые отвечают биологической целесообразности, лучше приспособлены к природным условиям. Наиболее правдоподобно природа красоты была раскрыта в 60-х годах XX столетия известным психологом академиком Р.Х. Шакуровым. Им была предложена гипотеза о том, что красивы те черты лица, которые при зрительном восприятии укладываются в их корковый, обобщенный образ — в стереотипный усредненный стандарт, сформировавшийся в нашей голове в ходе общения с людьми [6, с. 81–82]. Сказанное отражает красоту форм. Другими составляющими красоты являются: ее эмоционально-экспрессивная сторона, обращенная к аффилиативной потребности, ассоциативно-эмоциональный компонент, оригинальность. Указанные составляющие проявляются в улыбчивых лицах, светящихся добротой и нежностью, в цвете лица, ассоциирующемся со здоровьем, в своеобразии, нестандартности [6, с. 84–85].

Очевидно, что указанное понимание красоты лица может быть перенесено на красоту любого объекта, в частности математического. Наиболее привлекательным будет тот объект, представление о котором соответствует сформировавшемуся образу этого объекта. Данный вывод совпадает с указанными математическими моделями эстетической привлекательности математических объектов. Ясно, что в случае затраты минимума усилий, а это возможно когда восприятие укладывается в обобщенный образ (по Шакурову), мера красоты возрастает, причем степень возрастания пропорциональна росту меры порядка. Отсюда следует, что для ученика красивыми математическими объектами будут те, восприятие которых учеником сопряжено с наименьшими его усилиями. Их привлекательность будет усиливаться за счет динамической составляющей красоты, выражаемой в оригинальности, неожиданности, изяществе.

С позиций сказанного следует внести коррективы в традиционно сложившуюся методику обучения школьников математике. Например, методика обучения доказательству рекомендует как можно раньше приобщать школьников к самостоятельному открытию фактов и способов их обоснования, хотя у учащихся еще нет даже самого простого представления о процессе доказательства, его составляющих. Само требование «доказать» не вызывает у них нужных ассоциаций. Замечу, что процесс самостоятельного поиска доказательства основывается на ряде логических и эвристических операций, многими из которых учащиеся 6–7-х классов не владеют. Поэтому на первых уроках геометрии 7-го класса следует воспользоваться готовыми доказательствами с целью изучения структуры логического вывода (наличия большой посылки, малой посылки), связей логических шагов. Для достижения этой цели можно воспользоваться специальными карточками с двумя колонками, в одной из которых указываются утверждения, в другой — обоснования, причем каждая колонка имеет пустые места, количество которых зависит от способностей школьника, заполняющего пропуски в колонках. Ясно, что сказанное не отменяет эвристического обучения2 и приобщения учеников к открытию доказательств. Однако, подчеркнем еще раз, самостоятельное доказательство должно основываться на понимании готового доказательства, порядка, что ведет к формированию устойчивых математических образов.

Учитывая, что у ученика с его взрослением развиваются пространственные представления об окружающем мире, приобретающие форму устойчивых образов реальных объектов, изучение элементов геометрии в 5–6-х классах естественно должно основываться на идее фузионизма (слияния); однако эта идея не должна быть стержневой. В основной школе должен изучаться систематический курс планиметрии, а в старших классах — курс стереометрии. Заканчивать изучение геометрии в средней школе следует знакомством школьников с аксиоматическим методом не только как методом организации математической теории, но и как эффективным эвристическим средством, а также выходом в геометрию четырехмерного пространства. Известно, что необходимость систематических курсов оспаривается некоторыми математиками и методистами. Они предлагают, в частности, единый курс планиметрии и стереометрии. Однако такой курс построить на достаточно строгом логическом уровне в основной школе невозможно. Такой курс будет представлять собой набор различных фактов, поэтому мера порядка его организации будет невысокой, а потому будет низкой и мера привлекательности такого курса для учащихся, что, несомненно, будет отражаться на их интересе к изучению такого курса, а следовательно и на знаниях и умениях школьников.

Необходимость учета зависимости меры красоты и привлекательности объекта от порядка и меры усилий на его понимание подтверждает и природа распознавания объектов: на уровне свернутого выполнения действий распознавание осуществляется не по логическим признакам, а по внешне выраженным, наглядным признакам используемых объектов. «Идеальный» вариант возникает тогда, когда определение понятия позволяет воображению легко конструировать образы определяемых объектов. В данном контексте, например, наиболее привлекательным среди возможных определений параллелограмма является классическое определение, так как оно в большей мере соответствует имеющемуся в мышлении ученика образу параллелограмма.

Известны многолетние дискуссии по вопросу использования алгебраического метода решения текстовых задач. Одни участники дискуссий выступают за раннее введение метода уравнений, другие считают, что основное внимание в начальной школе и в 5–6-х классах должно уделяться арифметическому методу.

С позиции красоты вряд ли будет казаться привлекательным для ученика 5-го класса решение текстовой задачи с применением уравнений или доказательство теоремы методом «от противного», потому что рассуждения, осуществляемые в процессе решения задачи либо в доказательстве теоремы, не будут для ученика естественными. Хотя текстовые задачи привлекательны для школьников, поскольку они отражают реальные ситуации, хорошо знакомые им.

Изначальным стимулом развития математического знания является потребность в решении конкретных практических задач, которая «неизбежно приобретает внутренний размах и выходит за рамки непосредственной полезности» [5, с. 19]. Поэтому использование текстовых задач в обучении математике на ранних этапах необходимо, однако спешить с применением уравнений при их решении не следует. Последнее предполагает ряд таких умений (моделировать словесно заданные ситуации, выражать заданные величины одну через другую и т. д.), которые как раз и формируются при решении текстовых задач арифметическим способом. Ученик, овладевший хотя бы некоторым опытом решения текстовых задач арифметическим методом, при встрече с алгебраическим методом будет, в какой-то мере, удивлен оригинальностью суждения при его использовании, и эта неожиданность будет усиливать привлекательность алгебраического метода.

Анализируя учебники геометрии для основной школы, мы видим, что метод «от противного» используется при решении задач уже на первых уроках геометрии, хотя учащиеся еще не осознали смысл прямого обоснования. Поэтому в такой ситуации применение этого метода может вызвать лишь неприязнь к изучению геометрии. Последнему будет способствовать и неопределенность требований первых задач курса геометрии.

Как уже было отмечено, важной характеристикой меры красоты является порядок, который выступает в различных формах. Наиболее распространенной из них является симметрия. Причем речь идет не только о симметрии как гармонии частей целого, их упорядоченности, но и как осознании стройности математических доказательств. Поэтому наиболее привлекательными для учащихся являются изящные доказательства. Отметим и такие характеристики красоты математики, как возможность влияния на дальнейшее продвижение в той или иной области на основе аналогии и обобщения, богатство возможных приложений как в математике, так и в смежных дисциплинах, оригинальность.

Под влиянием конкретной ситуации в коре головного мозга актуализируются определенные образы, бессознательно «ждущие» встречи с соответствующими объектами. Когда ожидание, основанное на обобщенном стандарте, беспрепятственно реализуется, это переживается как красота. В ситуации, когда воспринимаемый стимул похож на его корковую модель, но не укладывается в нее полностью, возникает удивление и связанный с ним познавательный интерес. Абсолютно новый стимул не вызывает интереса, поскольку он не представлен в психике, нет его стереотипного образа в голове [6, с. 88]. В связи со сказанным, в обучении важно использование различных рисунков к доказательству теоремы, упражнений на распознавание объектов, принадлежащих формируемому понятию, различных способов доказательства, самостоятельного открытия теорем, оригинальных способов решений, укрупнения единиц, чертежей с одной основой, аналогичных задач, блоков «родственных» задач и т. д. Все это непосредственно связано с красотой, с механизмами эстетического воспитания школьников средствами математики, с выработкой эстетического вкуса путем формирования стандартов (устойчивых математических образов). Вспоминаю случай, когда во время перерыва после урока геометрии в 7-м классе вбежал в класс возбужденный ученик с криком: «Я доказал, что сумма углов четырехугольника равна 360°» (на уроке изучалась теорема о сумме углов треугольника). Удивление вызвала неожиданная догадка о том, что четырехугольник можно диагональю разбить на два треугольника. При отборе задач, их организации следует учитывать возможность актуализации привычных образных представлений, использования аналогии, обобщения, конкретизации, неожиданности, изящества в обосновании утверждений, общности исходных гипотез, связи с практическими ситуациями, естественного хода обоснования гипотез. Рассмотрим конкретные примеры.

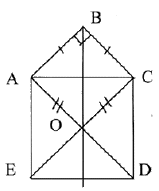Рис. 11. Дан прямоугольный треугольник ABC с прямым углом B. На его гипотенузе AC (вне его) построен квадрат ACDE с центром O. Доказать, что луч BO является биссектрисой угла ABC.

Возможно, что кто-то из учащихся, решавших эту задачу, и предложит один из способов ее решения. Однако может оказаться, что таких учащихся не найдется. В таком случае можно предложить рассмотреть частный случай, обусловленный тем, что треугольник ABC будет прямоугольным и равнобедренным. Чертеж, иллюстрирующий данную ситуацию, будет более привлекателен для учащихся, так как его восприятие в большей мере соответствует их житейским образам. Поэтому к такому рисунку будет проявлено большее любопытство.

Легко заметить, что фигура на рисунке 1 симметрична относительно прямой BO. Этот факт легко может быть и обоснован: точка B равноудалена от точек A и C, следовательно, она принадлежит оси симметрии этих точек. 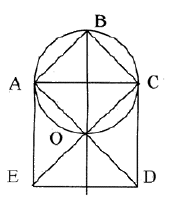Рис. 2Аналогично, этой же оси симметрии принадлежит и точка O. Значит, прямая BO — ось симметрии четырехугольника ABCO, а потому луч BO является биссектрисой угла B. Ясно, что обоснование доказываемого утверждения может быть выполнено и другим способом.

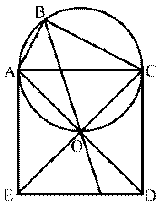
Устанавливаем, что четырехугольник ABCO — квадрат, около которого можно описать окружность. По отношению к ней углы ABO и OBC являются вписанными, опирающимися на равные дуги AO и OC (рис. 2). Легко заметить, что перемещая точку B по окружности (рис. 3), приходим к рисунку 4, который и соответствует данной задаче. Частный случай подсказал способ ее решения. Ясно, что идея симметрии в общем случае не срабатывает, однако она наталкивает на идею использования поворота вокруг точки O на 90°.

Пусть это будет поворот по часовой стрелке. Он переведет прямую AB в прямую BC, поскольку точка A перейдет в точку C, а прямая AB — в прямую, проходящую через точку C перпендикулярно к AB, то есть в прямую BC. Следовательно, точка O равноудалена от прямых AB и BC, а потому принадлежит оси симметрии угла ABC.

Рис. 3Решив данную задачу, следует обратить внимание учащихся на эвристики:

1) если в задачной ситуации имеется два прямоугольных треугольника с общей гипотенузой, то полезно для решения задачи ввести окружность, описанную около этих треугольников; 2) если в условии задачи даны две взаимно перпендикулярные прямые либо квадрат, то для ее решения можно воспользоваться поворотом вокруг центра квадрата на 90°.

Далее можно предложить рассмотреть случай, когда квадрат, построенный на гипотенузе AC, содержит точку B. В зависимости от уровня подготовленности класса можно продвинуться и далее. Например, прямоугольный треугольник можно заменить двумя взаимно перпендикулярными прямыми, проходящими через соседние вершины квадрата. Можно предложить учащимся составить несколько аналогичных задач, заменив квадрат, например, правильным треугольником. В этом случае две взаимно-перпендикулярные прямые должны быть заменены двумя прямыми, проходящими через соседние вершины треугольника и образующими угол в 120°. Указанная задачная ситуация может быть обобщена на правильный шестиугольник и т. д.

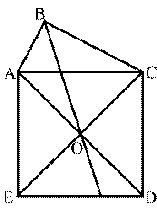Рис. 4Замечу, что исследование задачной ситуации с использованием обобщения, конкретизации и аналогии способствует созданию обобщенного образа этой ситуации, особенно в том случае, когда она является опорной, то есть используемой в большинстве задач изучаемого раздела. Встреча учащихся с рисунком, который отложился в памяти ученика, вызовет те ассоциации, которые были связаны с ним ранее и могут продвинуть решение задачи. Наконец отметим и то, что поиск решения задачи осуществляется посредством приема мысленного преобразования исследуемого объекта, что важно, потому что данный прием является эффективным эвристическим приемом в математическом познании. С другой стороны, решение подобных задач формирует сам указанный прием, а также приемы обобщения, аналогии, конкретизации и т. п.

2. Дан равнобедренный прямоугольный треугольник ABC (ÐC = 90°). Построен отрезок CC1 (C1ÎAB), перпендикулярный медиане AA1. Найти отношение BC1 : C1A.

Данная задача интересна тем, что допускает различные способы решения, хотя заключительный этап ее решения не богат возможностями конструирования новых задач. В журнале «Математика в школе» (№ 4/1981, с. 69) приведено пять способов решения задач, однако среди них нет самого простого способа, основанного на использовании координатного метода. Приведем его.

Введем систему координат так, чтобы прямая CA служила осью Ox, прямая CB — осью Oy (луч CA определяет положительное направление оси Ox, а луч CB — оси Oy); за единицу измерения примем длину отрезка AC. Тогда

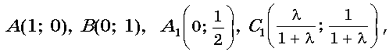
где . Уравнение прямой CC1 имеет вид:а уравнение прямой A1A –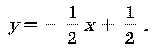

Используя условие перпендикулярности прямых, получаем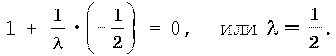 

Заключительный этап решения задачи обладает большим эстетическим потенциалом и служит хорошим средством формирования мотивации учебной деятельности школьника. Данный этап имеет значительные возможности для приобщения школьников к составлению задач, что связано с исследованием задачной ситуации.

3. Если хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.

Конкретизация задачной ситуации приведет к задаче, в условии которой хорды перпендикулярны и одна из них является диаметром. Поскольку в полученной задаче используется частный случай, то решение последней задачи распространяется и на решение полученной. Данная задачная ситуация может быть интерпретирована по-другому: из точки окружности проведен перпендикуляр к ее диаметру. Квадрат перпендикуляра равен произведению отрезков диаметра. Заметим, что конкретизация приводит к ситуации, когда имеется решение задачи, а сама задача должна быть сформулирована.

P.S. Обобщение основной задачи приводит к ситуациям:

1) прямые, которым принадлежат хорды, пересекаются вне круга, определяемого данной окружностью; 2) одна из секущих является касательной (предельный случай 1); 3) обе секущие являются касательными.

Далее возможен выход в задачную ситуацию, которую составляют две окружности и хорды каждой из них. Требуется найти такое положение точки пересечения хорд, которое удовлетворяет основной задаче. Возможен выход даже в три окружности, что обусловит уже исследование со всеми его атрибутами.

Привлекательность работы с задачей может быть повышена даже в процессе решения элементарных задач.

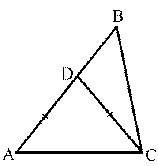Рис. 5Рассмотрим задачу. В треугольнике ABC биссектриса угла C пересекает сторону AB в точке D, AD = DC, ÐA = 40° (рис. 5). Доказать, что AB > BC.

Поскольку в треугольнике ABC известен угол A, то сравнение указанных сторон может быть осуществлено посредством сравнения углов, лежащих против данных сторон. На данную эвристику следует обратить внимание учащихся. Однако ее использование требует знания второго угла треугольника — угла C. Рисунок помогает увидеть, что ÐC содержит ÐACD, равный углу A. Таким образом, ÐC >ÐA, следовательно AB > BC.

Ясно, что приведенная задача не обладает возможностями построения на ее основе задач-обобщений, задач-конкретизаций, задач-аналогов и так далее. Однако на ее основе возможно конструирование целой серии задач. Вот требования некоторых из них (условия задач совпадают с условием данной задачи):

«Сформулируйте несколько утверждений, справедливость которых следует из условия данной задачи».

Ответ: 1) ÐACD=40°; 2) ÐC=80°; 3) ÐB=60°; 4) AC>BC; 5) AC<AB; 6) DC>BD; 7) AB>BC.

Рассмотрим следствие 7). Доказано, что AB>BC. Учитывая, что точка D находится между точками A и B, а AD=AB, то AD+BC>BC и, наконец, DC+DB>BC. Последнее неравенство, как легко заметить, будет справедливым при любой величине угла A и любом положении внутреннего луча CD. Важно лишь то, что AD=DC. Так приходим к обобщенной задаче: «На стороне AB треугольника ABC взята точка D так, что AD=DC. Докажите, что AB>BC». Данное неравенство DC+DB>BC приводит к выводу, что в треугольнике сумма двух сторон треугольника больше третьей стороны. Решение данной задачи не только мотивирует введение теоремы о неравенстве треугольников, моделирует ее доказательство, но и обосновывает ее для частного случая.

Сопровождая решение даже таких простых задач указанной работой с ними, мы повышаем их привлекательность и эстетический потенциал. Учащиеся начинают смотреть на задачи как на исследовательские объекты, в которых скрыта гармония и красота математики, наслаждаясь тем, что в процессе работы эти качества математики обнажаются, и красота математики становится для учащихся доступной.

Подведем итоги. Красота математики раскрывается в воспитании склонности школьников к использованию обобщения и аналогии, наглядной выразительности математических объектов, унификации и разнообразным приложениям тех или иных математических фактов и закономерностей, всестороннему анализу изучаемых ситуаций, минимально возможной субъективной сложности, требуемой для достижения того или иного результата, поиску различных способов решения задачи и выбору из них наиболее изящного, полной логической обоснованности и доказательности, склонности к поиску различных моделей рассматриваемых ситуаций, общности исходных гипотез, различных приложений изучаемых фактов.

Следует иметь в виду и эмоциональность формы подачи учебного материала. Монотонность изложения, безразличие учителя к излагаемому не вызовут эстетического удовлетворения школьников. Известно, что 38% информации человек получает из интонации, 55% — через жесты и мимику, и лишь 7% — из слов. Поэтому владение учителем интонацией голоса, мимикой и жестами есть одно из условий успеха в эстетическом воспитании школьников.

Литература

1. Адамар Ж. Исследование психологии процесса изобретения в области математики. — М., 1970. 2. Белл Э.Т. Творцы математики. — М., 1979. 3. Биркгоф Г. Математика и психология. — М., 1977. 4. Болтянский В.Г. Математическая культура и эстетика. — Журнал «Математика в школе», № 2/1982, с. 40–43. 5. Курант Р., Робинс Г. Что такое математика? — М., 1967. 6. Шакуров Р.Х. Эмоция. Личность. Деятельность (механизмы психодинамики). — Казань, 2001.

1 Изоморфизм — наличие взаимооднозначного отображения двух совокупностей, сохраняющего их структурные свойства. 2 Эвристика — совокупность приемов и методических правил теоретического исследования и отыскания истины; метод обучения, способствующий развитию находчивости, активности.

TopList

Занятие № 5 Школы Учителя математики

[14.07.2004]

На занятии № 5 в ШУМ-2 (г. Брянск) рассматривалась методика изучения теорем. План работы в первый день: 1. Выдвижение проблем, связанных с изучением теорем. 2. Анкетирование по методике изучения теорем. 3. Изучение теории по методике изучения теорем. 4. Методический анализ конспекта урока по теме «Третий признак равенства треугольников». Дадим комментарий содержанию первого дня занятия. Выдвижение проблем, связанных с изучением теорем, осуществлялось с использованием приема «вертушки». Учителя разбились на группы; от группы к группе передавались листы по определенным направлениям, на которых учителя записывали свои предложения. На работу с каждым листом группе отводилось 5 минут. По направлению «Хотим спросить, потому что считаем вопросы важными, хотя ответ на них знаем» учителя записали (смена стиля шифра в записи следующих вопросов говорит о смене группы учителей их задавших): 1. Какие этапы включает в себя методика изучения теорем? 2. Какими могут быть методы введения формулировки теоремы? 3. Какие требования являются обязательными при доказательстве теорем? 4. Какие вопросы желательно задавать на этапе усвоения теорем? 5. Стоит ли перед доказательством теоремы записывать план доказательства? 6. Стоит ли рассматривать все типы задач на этапе закрепления теоремы? 7. Как методически верно оформлять этап закрепления теоремы? 8. Можно ли теорему давать на самостоятельное изучение? 9. Какие методы можно использовать на подготовительном этапе изучения теорем? 10. Нужно ли все этапы изучения теорем рассматривать на одном уроке? 11. Какие записи возникают на доске на этапе работы с формулировкой теоремы? 12. Что обсуждается на этапе подведения итогов изучения теоремы? 13. На каком этапе осуществляется проверка формулировки и доказательства теоремы? Замечание. При подготовке к занятию учителя изучали теоретические основы методики изучения теорем: Методика изучения теорем включает следующие этапы: • подготовительный этап; • введение теоремы; • усвоение теоремы; • закрепление теоремы. На первом этапе осуществляется актуализация знаний, необходимых для доказательства теоремы, причем желательно использовать задачи, для решения которых применяется нужный теоретический материал, а не использовать фронтальный опрос теории. На этом этапе, по возможности, проводится мотивация изучения теоремы. Введение формулировки теоремы может осуществляться двумя методами: конкретно-индуктивным и абстрактно-дедуктивным. В первом случае используют практическую работу или задачу. Во втором случае формулируют теорему сразу. На этапе введения делают чертеж, разбивают формулировку на условие и заключение и делают краткую запись формулировки теоремы (Дано:..., Доказать:...), осуществляют доказательство теоремы. Обязательным требованием к доказательству теоремы является четкое выделение этапов доказательства. Однако не следует выделять много мелких этапов, поскольку в этом случае затруднено их запоминание. Если теорема сложная, то учитель сообщает ученикам идею доказательства, если теорема доказывается методом, известным учащимся, то ученики привлекаются к выделению этапов доказательства, если теорема “прозрачная”, то ученики либо сами открывают доказательство (для чего используются методы анализа или синтеза), либо самостоятельно изучают доказательство по учебнику. На этапе усвоения теоремы повторяется формулировка (Что было дано? Что требовалось доказать? Какова полная формулировка?), основные этапы доказательства (С чего начинали? Что делали дальше? Зачем? Какие теоремы использовались при доказательстве? Какова цель их использования?) и решаются задачи на непосредственное применение теоремы (задачи в один шаг) устного характера на готовых чертежах. На этапе закрепления осуществляется проверка формулировки и доказательства теоремы, и решаются более сложные задачи с применением изученной теоремы. Желательно выделять с учащимися ситуации, в которых применяется теорема. При подведении итогов обсуждается: с каким новым математическим фактом познакомились, какие математические понятия он характеризует, при решении задач каких видов используется этот факт. По направлению «Хотим спросить, потому что ответа на эти вопросы не знаем» учителя записали: 1. Как организовать работу на этапе усвоения теоремы так, чтобы в этой работе был задействован весь класс? 2. Какими способами можно проверить доказательство теоремы на следующем уроке? 3. Можно ли при изучении теоремы разрывать во времени этапы работы с нею? 4. Как научить детей различать теоремы-свойства от теорем-признаков. 5. Необходимо ли знать учащимся доказательства алгебраических теорем? 6. Как осуществляется подборка заданий для подготовительного этапа? 7. Можно ли доказывать некоторые теоремы по чертежу без записи доказательств. По направлению «Проблемы учащихся в связи с изучением теорем» учителя записали: 1. Страх перед теоремой у учащихся. 2. Не всегда могут расширить краткую запись доказательства. 3. Выполнение чертежа по условию теоремы. 4. Распознавание ситуаций применения теоремы. 5. Затрудняются в выделении условия и заключения теоремы, если она не содержит слова «если …, то …». 6. Затрудняются делать краткую запись формулировки теоремы: «Дано … Доказать …». 7. Затрудняются строить логическую цепочку доказательства. 8. Затрудняются в выборе метода доказательства. 9. Не понимают необходимости доказательства теорем. 10. Если теорема не выделена в учебнике как теорема (сформулирована как задача), то ее не записывают и не используют. По направлению «Какие теоремы хотелось бы изучать на занятиях и почему?» учителя записали: 1. Объем пирамиды (использование интеграла). 2. Теорема о плоскости, проходящей через одну из скрещивающихся прямых (сложное доказательство). 3. О разложении вектора по двум неколлинеарным векторам (мотивация введения нового числа). 4. Теорема Фалеса (рассматривается как задача).5. Площадь поверхности сферы (использование предела в доказательстве). 6. Теорема синусов и косинусов (использование специальных методов). 7. Теорема о площади криволинейной трапеции (громоздкое доказательство). 8. Признаки равенства треугольников (трудно воспринимается принцип доказательства). Признак параллельности прямых в учебнике А.В.Погорелова (метод от противного). Завершилась работа групп комментарием преподавателя, в котором раскрывался методический опыт по решению выдвинутых проблем. Вопросы, на которые учителя могли ответить самостоятельно, позволили повторить теорию по методике изучения теорем, с которой учителя заранее знакомились по методическому пособию «Базовые методики обучения математике». Анкетирование по методике изучения теорем включало следующие вопросы. 1. Перечислить этапы изучения теорем. 2. Сделать краткую запись формулировок следующих теорем: а) Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон, б) Для любого а и произвольных натуральных чисел т и п произведение степеней равно степени с основанием а и показателем, равным сумме т + п, в) Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника, г) Для того, чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы противоположные стороны были попарно конгруэнтны, д) Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину, е) Любая прямая в декартовых координатах имеет уравнение вида ах + ву + с = 0, где а, в, с – некоторые числа. 3. Определить, о какой теореме идет речь по ее краткой записи, и по описанию шагов доказательства сделать чертеж, дать обоснование шагам доказательства (использовался признак параллельности прямой и плоскости по учебнику А.В.Погорелова). 4. Прочитать доказательство признака перпендикулярности двух плоскостей в учебнике А.В.Погорелова Выделить по тексту доказательства цепочку рассуждений и описать ее по схеме: имеем …, значит, … (обоснование: …). Теория по методике изучения теорем включала следующие вопросы: 1) определение теоремы и ее структура; 2) виды формулировок теорем; 3) суть дедуктивного вывода; 4) необходимые (достаточные) условия, теоремы-свойства (теоремы-признаки); 5) виды теорем (прямая, обратная, противоположная, обратная противоположной, связь между ними и ее использование при доказательстве теорем. Завершилась лекция демонстрацией компьютерной презентации Н.С.Маевской «Признак перпендикулярности прямых», представленной на @педсовете 2003 года. Методический анализ конспекта урока по теме «Третий признак равенства треугольников» осуществлялся с использование распечатки: «Итак, ребята, вы уже изучили два признака равенства треугольников. Давайте их вспомним (ученики формулируют). А теперь ответьте, пожалуйста, на следующие вопросы: • Какой треугольник называется равнобедренным? • Дайте определение медианы треугольника. • Дайте определение высоты треугольника. • Чем является медиана в равнобедренном треугольнике, опущенная из вершины на основание? А теперь рассмотрим следующую задачу (учитель формулирует условие задачи по чертежу). Чему равен отрезок ВД? Мы видим, что три стороны одного треугольника равны соответственно трем сторонам другого треугольника, а равенство треугольников мы доказали по 1-ому признаку равенства треугольников. Следовательно, мы можем сказать, что если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Это утверждение называется третьим признаком равенства треугольников. (Записывается тема урока, формулировка читается учениками по учебнику, выделяются условие теоремы, ее заключение, составляется краткая запись формулировки теоремы, строится чертеж.) Допустим, что треугольники не равны, тогда что можно сказать об углах у этих треугольников (ученики отвечают, что углы не равны, так как иначе треугольники были бы равны по 1-ому признаку). Молодцы, правильно. А теперь давайте рассмотрим треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1 В1. Пусть Д – середина С1С2. Так как мы рисовали ∆ А1В1С2, равным ∆АВС, то у него А1С2 = АС, В1С2 = ВС, значит, ∆ А1С1С2 и ∆ В1С1С2 – равнобедренные, с каким общим основанием? (ответ – С1С2). Соединим Д с вершинами А1 и В1. Чем будут являться отрезки А1Д и В1Д для равнобедренных треугольников? (медианами). А чем является медиана в равнобедренном треугольнике? (высотой и биссектрисой). Нас сейчас будет интересовать то, что она является высотой. А высота – это что такое? (это перпендикуляр). Значит, А1Д С1С2 и В1Д С1С2¬. Посмотрите на рисунок: получается, что через одну точку полуплоскости мы провели два перпендикуляра, а разве это можно сделать? Получили противоречие, значит, наше предположение не верно. Тогда, что можно сказать о ∆АВС и ∆А1В1С1? Запишите доказательство к себе в тетрадь». Учителям было предложено задание: «Прочитайте фрагмент конспекта урока «Третий признак равенства треугольников», выделите в нем этапы работы, укажите цель каждого этапа. Дайте комментарий с позиций методики изучения теорем. Дайте комментарий с позиций учащихся». Учителя выделили следующие этапы: 1. Подготовительная работа. 2. Введение теоремы: а) Введение формулировки; б) Работа с формулировкой и построение чертежа; в) Доказательство теоремы: • предполагают противоположное тому, что требуется доказать; • выбирают третий треугольник, равный первому в заданном расположении относительно второго; • работают с равнобедренными треугольниками и получают противоречие; • делают выводы. С позиций методики изучения теорем учителя сделали следующие замечания: 1) подготовительный этап осуществлялся с помощью опроса, хотя рекомендуется использовать соответствующие задачи; 2) переход от задачи к формулировке теоремы логически неверен, т.к. в задаче использовалось определение (если треугольники равны, то равны соответствующие стороны), а в формулировке признака пытаются сформулировать утверждение, обратное части определения. Трудным оказался анализ конспекта с позиций учащихся. Важно было определить, согласуется ли имеющийся опыт учащихся с методическими действиями учителя, и, в случае необходимости, исправить методические ошибки учителя. Перечислим методические ошибки учителя: 1) необходимо мотивировать, почему третий признак не доказывается так, как первые два; 2) дополнительные построения не мотивированы; 3) логический вывод о единственности перпендикуляра может оказаться для учащихся не достаточно убедительным, поскольку он не согласуется с рисунком. На занятии были исправлены допущенные методические ошибки. Удачным был прием использования черновиков при доказательстве теорем. План работы во второй день: 1. Гуманитарная составляющая теорем. 2. Практикум по составлению плана и конспекта урока. 3. Подведение итогов первого семестра и постановка домашнего задания. Дадим комментарий содержанию второго дня занятия. Начался день с обсуждения гуманитарной составляющей теорем. Организовала обсуждение и подготовила раздаточные материалы аспирантка Брянского государственного университета И.А.Котова. Каждый учитель получил следующий текст: «Что следует понимать под гуманитаризацией математического образования? Обсуждение принципа гуманитаризации математического образования в научно-методической литературе показывает, что одни авторы гуманитаризацию сводят к развитию логического мышления школьников посредством математики; другие рекомендуют усилить в содержании прикладные аспекты, особенно в социальных и гуманитарных областях знаний; третьи связывают гуманитаризацию с введением элементов историзма в содержание и т.д. Например, А.А.Столяр гуманитаризацию образования понимает как «увеличение в нем удельного веса гуманитарных дисциплин» (А.А.Столяр. Роль математики в гуманитаризации образования //Математика в школе, 1990, № 6, С.6). Н.Я.Виленкин видит решение проблемы гуманитаризации школьного курса математики в изучении истории математики и в применении математики в гуманитарных науках. Г.В.Дорофеев, говоря о гуманитарных аспектах математики, упор делает на формирование научного мировоззрения школьников посредством истории математики и обсуждением особенностей математического языка. А.А.Касьян считает, что «гуманиторизовать образование – значит сделать его … значимым для каждого данного человека (А.А.Касьян. Контекст образования: наука и мировоззрение. – Н.Новгород, 1996, С.143). Докторская диссертация Т.А.Ивановой связана с проблемой гуманитаризации математического образования. Согласно ее точке зрения, под гуманитаризацией образования, в том числе и математического, понимается «процесс, направленный на усвоение личностью гуманитарного знания, гуманитарного потенциала каждой изучаемой области знаний, на присвоение (интериоризацию) личностью общественно значимых ценностей» (Т.А.Иванова. Гуманитаризация общего математического образования: Монография. – Н.Новгород, 1998, С.32). Основную задачу гуманитаризации образования Т.А.Иванова определяет следующим образом: «сделать общественно значимые ценности образования любого вида личностно значимыми для каждого человека» (там же). Расшифруем такие понятия как «гуманитарное знание», «гуманитарный потенциал». Гуманитарным потенциалом в содержании общего математического образования являются методология научного поиска в математике, история математики. Методология научного поиска включает в себя: • предмет и метод математики, ее ведущие идеи и понятия, связь с другими науками и практикой (математическое моделирование), математический язык; • процесс познания; • методы научного познания (как общие эвристические и логические, так и частные, специфические); • культуру мышления, включающую и стиль научного мышления (Т.А.Иванова. Гуманитаризация общего математического образования: Монография. – Н.Новгород, 1998, С.127). Другим важным компонентом гуманитарного потенциала математического содержания является творческая (поисковая) математическая деятельность. Освоение учеником опыта творческой поисковой деятельности на уровне его возможностей позволит решить задачу овладения им гуманитарными знаниями. «Овладение школьниками гуманитарным потенциалом каждой области знаний обеспечивает и дальнейшее саморазвитие» - отмечает Т.А.Иванова (там же, С.33). «Гуманитарное знание в образовании – знание, которое получено самим учеником в результате его поисковой деятельности» (там же, С.32). Таким образом, когда гуманитарный потенциал присваивается учеником, это и есть гуманитарное знание, полученное учеником в результате его напряженной интеллектуальной, эмоционально окрашенной деятельности, которое понято и осмыслено им. Несомненным является еще и тот факт, что гуманитаризация образования предполагает переосмысление всех компонентов системы обучения: целей, содержания, методов, форм и средств обучения». По представленному тексту учителя получили задание: сформулировать вопросы, на которые можно найти ответ в тексте. Учителя сформулировали следующие вопросы: 1. Чьи точки зрения на проблему гуманитаризации отражены, в чем суть каждой? 2. В чем особенностей взгляда Т.А.Ивановой на гуманитаризацию? 3. Какова задача гуманитаризации по Т.А.Ивановой? 4. Что включает в себя гуманитарный потенциал (каковы компоненты)? 5. Что такое гуманитарное знание? 6. Какова связь между гуманитарным потенциалом и гуманитарным знанием? 7. Какие изменения предполагает гуманитаризация в образовании? 8. Как овладеть ученику гуманитарными знаниями? 9. Связана ли гуманитаризация с развитием личности? 10. Что включает в себя методология научного поиска? Дальнейшее обсуждение строилось вокруг обозначенных вопросов. Так, при обсуждении первого вопроса, учителя не только перечисляли различные точки зрения, но и высказывали свое мнение относительно того, чья точка зрения им ближе и почему. При обсуждении вопроса о связи между гуманитарным потенциалом и гуманитарным знанием учителя составили следующую последовательность своей деятельности по выявлению гуманитарного потенциала математики и превращению его в гуманитарные знания: 1) провести анализ содержания школьных учебников с целью выявления: идей; методов; приемов, отраженных в этом содержании (например, в доказательстве теорем, в особенностях ее применения); 2) просмотреть книги по истории математики; 3) продумать организацию деятельности учащихся на уроке, чтобы они были включены в творческую (поисковую) деятельность; чтобы на этапе рефлексии этой деятельности произошло осмысление гуманитарного потенциала. С целью усвоения теоретического материала по проблеме гуманитаризации образования был предложен практический материал, связанный с изучением площади трапеции, который приведен в монографии Т.А.Ивановой. Практикум по составлению плана и конспекта урока начался с анализа плана урока по теме «Третий признак равенства треугольников», составленного И.Е.Маловой. В плане указаны цели урока; выделены этапы урока; сделаны чертежи задач; оформлено доказательство теоремы так, как планируется записать ученикам в тетрадях; прописаны вопросы учебных диалогов. На полях указана та информация, которую необходимо найти оперативно: материал, который заранее надо подготовить на доске; модели подобных треугольников; приемы организации деятельности учащихся; ключевые вопросы диалога, сопровождающие те или иные записи на доске и др. По ходу урока учителю важно на полях фиксировать свои и ученические находки, затруднения, ошибки и пр. Приведем отрывки плана урока по теме «Третий признак равенства треугольников». Цели: 1) изучить третий признак равенства треугольников; 2) выделить условия, из которых может следовать равенство сторон; 3) познакомиться с приемом доказательств, когда каждый следующий этап сводится к предыдущему; с трихотомией в связи с расположением точки; 4) обогатить опыт учащихся по поиску новых фактов через перебор возможностей; по использованию моделей для поиска логических противоречий. После решения задачи по готовому чертежу, в которой использовался 1-ый признак, следует диалог: • Какие элементы треугольника участвуют во 2-ом признаке? • Что общего в этих двух признаках? (участвует три элемента; участвуют стороны, углы треугольников). • Какие иные сочетания трех элементов треугольника могут быть? • Попробуйте сформулировать утверждение о равенстве 2-х треугольников, если 3 угла одного треугольника соответственно равны 3-м углам второго треугольника. Верно ли это утверждение? • Попробуйте сформулировать утверждение о равенстве 2-х треугольников, если 3 стороны одного треугольника соответственно равны 3-м сторонам второго треугольника. • Верно ли, что 3-и стороны треугольника, который построил дома …(называется имя ученика – И.М.), равны 3-м сторонам треугольника, который построил дома …? Верно ли, что построенные треугольники равны? Как это проверить (учащиеся поднимают свои модели с проверкой). Надо ли доказывать этот факт? На этапе усвоения доказательства следует диалог: Как называется теорема, которую доказали? Как она звучит? С чего начинали доказательство? (Рассматривали 3-ий треугольник…). Какие случаи расположения С2 рассматривали дальше? Какие выводы делали в первых двух случаях? С какими фигурами работали в 3-ем случае? Какие дополнительные построении делали? К какому выводу пришли? Что полезного желательно запомнить на будущее из рассмотренного доказательства? 1) полезно рассматривать различные случаи расположения одной и той же точки относительно данных фигур; тот случай, который не устраивает отвергаем методом от противного (Было: т.Паша, “какая из трех точек…”; будет теорема о вписанном угле); 2) Доказательство одного этапа может сводиться к предыдущему этапу; 3) Построение медианы к основанию равнобедренного треугольника как дополнительное построение. Для этапа усвоения теоремы учитель приготовил 5 чертежей: на первом даны два треугольника и указано равенство трех пар элементов; на втором – заданы линейные размеры сторон; на третьем – изображен параллелограмм, проведена диагональ и указано равенство противоположных сторон параллелограмма; на четвертом – дан равнобедренный треугольник и проведена высота к основанию; на пятом – изображен прямоугольник и в нем проведены две диагонали. При решении задач по готовым чертежам звучат вопросы: Чем задача 2 отличается от предыдущей? Чем задача 3 отличается от 1-ой? Можно ли решить задачу 4, используя другие признаки равенства треугольников? Чем отличается задача 4 от задачи 3, если использовать 3-ий признак? Можно ли в задаче 5 сразу доказать равенство требуемых треугольников (а каких можно; помогут ли они)? Продолжился практикум обсуждением технологии составления плана урока по теме «Следствия из аксиом стереометрии» на основе материалов изучения теоремы о существовании плоскости, проходящей через прямую и не лежащую на ней точку, изложенных в пособии «Базовые методики обучения математике». Завершилось занятие подведением итогов первого семестра и постановкой домашнего задания. Подведение итогов было организовано в форму круглого стола; каждый слушатель рассказал о себе, о том, что дали ему занятия в ШУМе, какие изменения в практике преподавания наметились и др. К занятию № 6 было предложено выполнить следующее домашнее задание: 1) вернуться к анкете по методике изучения теорем и исправить обнаруженные ошибки; 2) разработать по подгруппам методику изучения теорем (без этапа закрепления): • объем пирамиды (учебник Л.С.Атанасяна); • разложение вектора по двум неколлинеарным векторам (учебник Л.С.Атанасяна); • признак параллельности прямых в пространстве (учебник А.В.Погорелова); 3) повторить текст о методике изучения теоремы о существовании плоскости, проходящей через прямую и не лежащую на ней точку (на занятии по этому тексту будет составлен план урока). Двое слушателей получили индивидуальные задания по подготовке компьютерных презентаций в связи с изучением теорем: площадь сферы; объем пирамиды (учебник А.В.Погорелова).

Школа учителя математики

[ И.Е. Малова ]