Занятие № 6 Школы Учителя математики
После летних каникул
в "Школе учителя математики" (ШУМ) продолжились занятия. Ирина
Евгеньевна Малова (г. Брянск) вместе со своими коллегами на занятии № 6
продолжает рассматривать методику изучения теорем.
План
работы в первый день:
- Обсуждение удач и ошибок при конструировании
методики формирования умений (по результатам контрольной работы № 2).
- Теория и методика изучения теорем (повторение).
- Практикум по составлению планов урока изучения
теоремы стереометрии (с использованием методического пособия).
- Конструирование фрагмента урока изучения конкретной
теоремы (работа в группах).
Дадим комментарий содержанию первого дня
занятия.
Удачи при конструировании
методики формирования умений были внесены в методические материалы
(распечатки), которые участниками ШУМА анализировались и комментировались на
занятии. Рассматривались методические удачи по мотивации, введению, усвоению
алгоритма соответствующего умения.
Мотивация умению
|
Умение
|
Мотивация
|
|
1. Решение двойных неравенств. Л.И.Михалева).
|
Сегодня научимся решать
неравенства нового вида. (Мотивация
через установление связи с изученным).
|
|
2. Решение неравенств методом
интервалов (Л.В.Маслова)
|
Через сопоставление неравенств,
содержащих два и три множителя. Первое сводится к известным методам, второе
мотивирует новый метод. (Мотивация через проблематизацию).
|
|
3. Вычитание смешанных чисел (5
кл.) (Н.В.Фролова)
|
Продолжаем изучать тему «Смешанные
числа». Что мы уже знаем о смешанных числах? (учащиеся перечисляют, включая
выполнение операции сложения). Какую операцию будем рассматривать сегодня?
(Мотивацию осуществляют учащиеся).
|
|
4. Решение иррациональных уравнений
в 8 классе, когда уравнение содержит несколько корней. (Н.А.Екимова)
|
На предыдущем уроке мы
познакомились с иррациональными уравнениями и одним из методов их решения. Сегодня
мы продолжим работу по этой теме, т.к. способов решения, как и видов
иррациональных уравнений, гораздо больше. 1.
Из указанных уравнений выберите иррациональные уравнения: а) 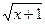 = 3; = 3;
б) 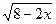 = х; в) х2 + 4 = х; в) х2 + 4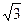 х
+ 12 = 0; г) х
+ 12 = 0; г) 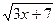 + + 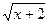 = 3. = 3.
2. Уравнения какого вида мы умеем решать? (учащиеся называют примеры
а и б). Покажите решения.
3. Сформулируйте задачу сегодняшнего урока. (Мотивация через …)
|
Введение алгоритма
Решение двойных неравенств
(Л.И.Михалева)
Группы
самостоятельно решают системы двух неравенств с одной переменной, причем левая
часть каждого из неравенств системы – одно и то же выражение. По завершении
работы, учащимся предлагается так сформулировать это задание, чтобы в
формулировке не звучали слова «решите систему неравенств». Так учащиеся
приходят к формулировке: «Решите двойное неравенство».
При
обосновании способа решения учитель использует прием «сначала сделаем, что
умеем» (закрывается левая часть двойного неравенства, и решается неравенство
привычным способом с фиксацией «на полях» выполняемых преобразований).
Аналогичные действия с закрытой правой частью убеждают учащихся, что преобразования
выполняются одни и те же, значит, есть смысл их выполнять одновременно для двух
частей неравенства.
Вычитание смешанных
чисел (Н.В.Фролова)
Составьте примеры на вычитание
смешанных чисел (все разные случаи составленных учащимися примеров выносятся на
доску). Какие из выписанных примеров могли бы решить? Кто объяснит решение?
Решение иррациональных
уравнений в 8 классе (Н.А.Екимова) типа 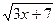 +
+ 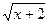 = 3.
= 3.
Рассмотрим
это уравнение. В чем сходство и отличие его от других уравнений? (это уравнение
тоже иррациональное, т.к. содержит переменную под знаком корня; но корней в нем
два). Оказывается, изученный метод (метод возведения обеих частей в квадрат) применим
и для данного уравнения. Прочитайте решение этого примера в учебнике (С.158,
А.Г.Мордкович), выделяя этапы его решения. (После обсуждения учащиеся без
учебника воспроизводят в тетрадях решение; кто-то это делает молча у доски;
после обсуждения правильности записей учитель демонстрирует значки-пометки «на
полях», демонстрирующие суть каждого преобразования).
Усвоение алгоритма
Решение системы
неравенств с одной переменной (Н.А.Винокурова):
1. Какие из предложенных систем
могли бы решить? (в списке: «нормальные» системы; системы, содержащие
неравенства, которые пока решать не умеют (с модулем, иррациональные, дробные);
системы трех неравенств; системы, где одно уравнение и одно неравенство;
системы неравенств с двумя переменными).
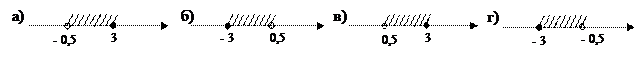 2.
На каком из рисунков изображено множество решений системы неравенств:
2.
На каком из рисунков изображено множество решений системы неравенств: 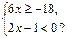
Нахождение неизвестного члена пропорции (И.Д.Демиденкова)
1. Из уравнений, записанных на
доске, выпишите в первый столбик те, которые можно решить новым способом. …
Объясните, почему вы выписали именно эти.
2.
Для каждого выписанного уравнения выполните первый шаг алгоритма и запишите результат
этого шага во второй столбик.
3.
Для каждого полученного уравнения выразите х и запишите результат этого шага
в третий столбик.
4.
Обсудим полученные выражения. Назовите варианты вычисления каждого из них (устно).
Умножение алгебраических дробей (О.Н.Бурковец). Закончите умножение:
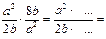 …;
…; 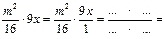 …; (учителям предлагается
продолжить список примеров так, чтобы встретились все возможные ситуации
умножения).
…; (учителям предлагается
продолжить список примеров так, чтобы встретились все возможные ситуации
умножения).
Решение иррациональных уравнений в 8 классе (Н.А.Екимова) типа 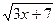 +
+ 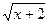 = 3.
= 3.
Какие умения пригодились в
решении уравнения нового вида? В каких шагах решения уравнений нового вида
считаете нужным потренироваться? Выберите из учебника соответствующие номера
(№684, 685).
Интересно
1. Творческое задание на дом:
используя многочлены 3х + 5; 2; 2 – 5х, составьте все возможные иррациональные
уравнения и постарайтесь их решить (Н.А.Екимова).
2. Карта по геометрическим
умениям может быть связана не только с вычислительными задачами, но и с
задачами на построение, например, карта по умению строить треугольник по
трем элементам (С.М.Хвастова).
3. Учитель Н.А.Екимова представила рекламу методов решения линейных
уравнений с двумя неизвестными:
При решении задачи не надейтесь на удачу.
Знать вам надо непременно много способов решенья.
Всем поможем без проблем мы в решении систем.
Если вам важно решений количество,
В ассортименте есть метод графический!
В выражении переменных вы, конечно, очень ловки?
Вам предложим, непременно, верный метод подстановки!
Есть эксклюзивное нововведение.
Вам не встречался ведь метод сравнения?
Тем, кто не выбрал ни тот и ни
этот,
Мы предлагаем сложения
метод!
Тем, кто рекламу читал невнимательно,
За разъясненьями – к рекламодателю.
Всем предлагает проекты свои!
Сертификат выдавал МПИ!
Анализ
ошибок по методике формирования умений осуществлялся с помощью
распечаток. К ошибкам были отнесены:
отсутствие мотивации; осуществление актуализации знаний, при которой учащиеся оказываются
в роли объектов, а не субъектов обучения; нарушение правил ведения учебного
диалога на этапе введения алгоритма; ошибки в формулировках алгоритмов; ошибки
при конструировании упражнений на отработку отдельных шагов алгоритма;
подведение итогов введению и усвоению алгоритма касалось только ключевого
математического содержания и не включало обсуждение его особенностей и процесса
работы с ним. На занятии учителя давали аргументированный ответ, почему такие
промахи являются методическими ошибками; анализировали варианты их исправления,
предложенные И.Е.Маловой.
Мотивация умению
|
Умение
|
Мотивация
|
|
1. Решение системы неравенств с
одной переменной.
|
Предлагается задача, связанная
с графиком функции, которая приводит к системе уравнений. Возникает проблема
ее решения.
|
|
2. Решение систем уравнений методом
подстановки (8кл.).
|
Для новых систем попробуем
применить старые методы. Какой попробовали? (графический) Какие остались? (учащиеся
перечисляют). Сегодня рассмотрим метод подстановки.
|
|
3. Нахождение неизвестного
члена пропорции.
|
В химии, физике, жизни и т.д.
при решении задач бывает нужно составить пропорцию. Часто бывает так, что
один из членов пропорции оказывается неизвестным, например, х : 7 = 13 :
0,4. Наша сегодня задача: выяснить, можно ли в такой ситуации найти
неизвестный член, и если «да», то как это сделать.
|
Актуализация знаний
Задания должны быть мотивированы, и учащиеся должны быть субъектами обучения.
Конструкция диалога: «Итак, мы сегодня будем работать с … Давайте вспомним, что о … знаем и что умеем делать?
(учащиеся перечисляют, учитель фиксирует это на доску). Приведите свои примеры.
Задайте вопросы в связи с перечисленным материалом».
Почему такие рекомендации?
__________________________________________________
Формулировка алгоритма
1. Формулировка нового алгоритма (например, решения двойных неравенств
первой степени) должна быть идентична
формулировке старому алгоритму (алгоритму решения неравенств первой степени), если идентичны шаги. Почему?
____________________________________________
Каков алгоритм решения двойных
неравенств первой степени? _____________________________________________________________________________
2. Формулировка должна
быть, по возможности, короткой. Почему?
_________________________________________________________________________
Каков алгоритм решения системы неравенств с одной переменной?
(решить каждое, нанести решения на одну числовую прямую, указать пересечение
решений (или общие решения), записать ответ).
3. Формулировка должна
быть, по возможности, простой. Почему?
_________________________________________________________________________
Каков алгоритм вычитания смешанных чисел в 5 классе?
(определить, можно ли сразу вычитать; если «да», то из целой части вычесть
целую, а из дробной – дробную; если «нет», то занять единицу и перевести ее в
дробную часть). В опыте учащихся был аналог – поразрядное вычитание натуральных
чисел (занять единицу и перевести ее в нужный разряд).
4. Формулировка не
должна содержать «мелких» шагов; желательно мелкие шаги обобщать в один
«большой». Почему? ________________________________________________
Объедините следующие шаги алгоритма нахождения неизвестного
члена пропорции: «назовите средние и крайние члены пропорции» и «используйте
основное свойство пропорции» в один шаг, чтобы в нем звучало слово «уравнение»,
т.к. все последующее обоснование опирается на понятие уравнения.
_________________________________________________________
Введение алгоритма
|
Умение
|
Диалог
|
|
1. Решение системы неравенств с
одной переменной.
|
Что значит решить систему
неравенств с одной переменной? (найти такие х, которые удовлетворяют
каждому неравенству) Что умеем? (находить такие х, которые удовлетворяют первому
неравенству, второму). Поможет ли?
|
|
2. Метод интервалов
|
Мы уже сталкивались с
неравенствами, правая часть которых – число 0. Приведите пример. Каким методом
решали такие неравенства? (графически; напоминают алгоритм). Попробуйте
построить какой-нибудь график функции, если будет известно, что в данных 4-х
точках (рис.) f(x) = 0.
(хорошо, если кто-то построит функцию с кратным нулем). Сможем ли теперь
решить неравенство f(x) > 0;
f(x) < 0? Имея одни и те же нули
функции, вы построили разные графики, значит, нужно что-то еще знать о
функции, чтобы можно было прикинуть, как располагается график. Идеи? (если
идей не будет, то играем: известно, что f(1) = 5; чей построенный
вами график претендует на роль f(x) ?...).
Итак, что надо знать, чтобы решить неравенство, в правой части которого – число
0? (нули и знаки соответствующей функции на интервалах). Из списка неравенств
выберете те, которые можно решить новым методом. Из выделенных неравенств
выделите те, для которых легко найти нули функции (так приходим к признакам: произведение
сравнивается с нулем; коэффициент при х равен 1).
|
|
3. Система уравнений, одно из которых
2-ой степени.
|
Что общего у системы 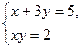 и любой из 7 класса,
которые мы решали методом подстановки (есть уравнение 1-ой степени)? Чем они
отличаются? Сможем ли применить метод подстановки? Сделаем прогноз: когда мы
подставим значение х
во второе уравнение, то уравнение какого вида получим? Сколько корней оно
может иметь? Как тогда найдем ответ для системы? и любой из 7 класса,
которые мы решали методом подстановки (есть уравнение 1-ой степени)? Чем они
отличаются? Сможем ли применить метод подстановки? Сделаем прогноз: когда мы
подставим значение х
во второе уравнение, то уравнение какого вида получим? Сколько корней оно
может иметь? Как тогда найдем ответ для системы?
|
|
4. Нахождение неизвестного
члена пропорции.
|
Проанализируем пример: х : 7 = 13 :
0,4. Мы сказали, что это пропорция, а о пропорции все, что знаем, повторили,
может ли что-то из этой копилки знаний сейчас помочь? (намечается план работы
с пропорцией).
Давайте по-другому посмотрим на наш
пример. Что о нем мог бы рассказать ученик 5 класса, который еще пропорцию не
изучал? (это уравнение). Можем ли мы воспользоваться этим фактом? (Учащиеся
выбирают порядок «опробования» способов: старый (упрощение правой части,
нахождение неизвестного делимого) – новый (с опорой на свойство пропорции)).
|
|
5. Умножение алгебраических
дробей.
|
Итак, сегодня разбираемся с
умножением алгебраических дробей. Приведите примеры, относящиеся к нашей
теме. Какие знания помогли нам разобраться
со сложением алгебраических дробей? (сложение обыкновенных дробей). Приведите
свои примеры на умножение обыкновенных дробей и напомните нужное правило.
Зачем мы обращались к обыкновенным дробям? Как теперь поступим? (выскажем
гипотезу, как умножать алгебраические дроби). В алгебре все должно быть
доказано. Попробуем. … Итак, доказали правило. Посмотрим на составленные вами
примеры и определим, можно ли применить к ним это правило? А теперь
проанализируйте два решения примера 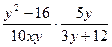 (в одном случае –
числители и знаменатели сначала раскладываются на множители, потом
применяется правило; во втором случае – сразу применяется правило, но в
записи пропущены скобки). Сделайте выводы о работе с подобными примерами. (в одном случае –
числители и знаменатели сначала раскладываются на множители, потом
применяется правило; во втором случае – сразу применяется правило, но в
записи пропущены скобки). Сделайте выводы о работе с подобными примерами.
|
Конструирование упражнений на
отработку шагов
1. Терминология шаговых заданий, по возможности, должна быть такой, как в
алгоритме.
Почему? ____________________________________________
Как сформулировать шаговые
задания для следующих умений: решение
двойных неравенств первой степени; решение систем неравенств с одной переменной;
решение неравенств методом интервалов; решение систем уравнений методом
подстановки (8 кл.); умножение алгебраических дробей?
Осуществите проверку своих ответов по конструированию шаговых заданий
Решение двойных неравенств первой степени:
1)
Даны двойные неравенства, центральная часть которых –
двучлен первой степени. Перенесите члены без переменной в крайние части неравенства
(Возможен вопрос: «Какой шаг надо сделать сейчас, чтобы продолжить решения
неравенств? Выполните его»).
2)
Даны двойные неравенства, центральная часть которых –
одночлен первой степени. Разделите все части неравенства на коэффициент перед неизвестной
(Возможен вопрос: «Какой шаг надо сделать сейчас, чтобы продолжить решения
неравенств? Выполните его»).
3)
Даны двойные неравенства, центральная часть которых
содержит скобки. Проанализируйте каждое неравенство и определите, можно ли
сразу указать ответ? Если «нет», то что мешает? Что будем делать? Как? Что
будем делать дальше? Где надо быть особенно осторожным?
Решение систем неравенств с одной переменной:
1)
Даны системы, в левой части каждого неравенства стоит
только х. Нанесите решения каждой системы
на одну числовую прямую.
2)
Даны числовые прямые, на которых отмечены решения 1-го
и 2-го неравенства. Выделите общие решения и запишите ответы систем с помощью
промежутков.
Решение неравенств методом интервалов:
1)
Даны неравенства, левая часть которых – произведение, а
правая часть – число 0. Приведите неравенства к виду, по которому легко
находить нули функции и определять знаки на промежутках. (Учащиеся приводят
неравенству к виду, когда коэффициент при х равен 1 и х стоит на первом месте).
2)
Даны неравенства, «подготовленные» к работе с
интервалами. Нанесите нули соответствующей функции на числовую ось и определите
знаки функции на полученных интервалах.
3)
Даны неравенства и соответствующие им изображения на
числовой оси. Запишите ответ неравенства.
Решение систем уравнений методом подстановки (8 кл.):
1)
Даны системы. Определите, из какого из 2-х уравнений удобно
выразить одну из переменных? Почему не из другого? Какую именно переменную
будем выражать? Можно ли другую? Почему тот (или иной) вариант
предпочтительнее?
2)
Даны системы, первое уравнение имеет вид: у = …(или х = …), а 2-е – квадратное. Доведите решение до конца.
Умножение алгебраических дробей
Даны примеры типа: 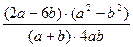 и
и 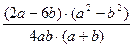 . Требуется сократить
дробь.
. Требуется сократить
дробь.
2. Не желательно, чтобы шаговые задания содержали обратные действия, но
желательно, чтобы содержали все
возможные случаи.
Почему?
____________________________________________
Вычитание смешанных чисел (5 кл.)
Исключите лишние примеры в задании
на заполнение пропусков и добавьте необходимые, на Ваш взгляд, примеры для
отработки занимания единицы:
а) 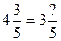 ; б)
; б) 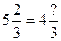 ; в)
; в) 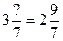 ; г)
; г)  .
.
Чтобы учащиеся формулировали шаг
алгоритма, можно обсуждать вопрос: «Что надо сделать, чтобы заполнить пропуск,
например, в примере а?» (надо занять
единицу и перевести ее в дробную часть).
Подведение итогов этапам введения
и усвоения алгоритма
Вопросы должны касаться не только
ключевого содержания (чему учились, каков алгоритм), но и его особенностей, а
также процесса работы с ним.
Какие это вопросы?
______________________________________________
Включили ли вы в свой ответ
вопросы:
- Какие случаи бывают?
- Каково обоснование алгоритму?
- Как себя проверять?
- С какими трудностями встретились, как их преодолели?
- Какие ошибки можно допустить, как их избегать;
какие примеры требуют повышенного внимания; …?
Теория
и методика изучения теорем повторялись в следующем режиме. Сначала была
дана мотивация: «С целью подготовки к третьему вопросу занятия (к практикуму по
составлению планов урока изучения теоремы) и к контрольной работе № 3 (в
которой необходимо представить планы двух последовательных уроков) важно
повторить изученное на прошлом занятии. Сформулируйте вопросы, которые вы
хотели бы выяснить при повторении».
Учителя
спросили: 1) что такое фронтальный опрос при традиционном и при личностно
ориентированном обучении; 2) как составлять задачи для подготовительного этапа
изучения теорем; 3) можно ли доказывать теоремы без записи доказательства; 4) в
чем заключается метод воображаемого построения; 5) как вести учебный диалог при
изучении доказательства; 6) что такое задачи в один шаг, которые используются
на этапе усвоения теоремы; зачем они нужны?
На
сформулированные вопросы учителя в обсуждении самостоятельно дали ответы.
Практикум
по составлению планов урока изучения теоремы стереометрии (с использованием
методического пособия) проходил в виде деловой игры. Каждый учитель получил по
четыре клейких листочка, на которых им необходимо было написать план изучения
теоремы-следствия из
аксиом стереометрии (о задании плоскости с помощью прямой и точки).
Составленные учителями планы были вывешены на доску вместе с планом
И.Е.Маловой. Такая «выставка» позволила увидеть различные подходы к пониманию
сути урочных планов; удачи и ошибки в фиксации или пропусках методических
моментов, связанных с изучением теоремы. Поскольку ошибок в составлении планов
урока было много, важно было понять причины их возникновения. Для этого учителя
постарались дать ответ на вопрос: «Зачем они составляют планы уроков?». Вот их
ответы:
«Отражаю порядок (ход) урока.
Прописываю математическое обоснование, которого нет в учебнике. Отражаю виды
деятельности учащихся, фамилии тех, кого надо спросить, тех, кого не следует
спрашивать на соответствующие задания. Обеспечиваю плотность урока. План нужен
для систематизации собственных мыслей по всему уроку. Указываю своими значками
то, на что надо обратить особое внимание. Выделяю опорные задачи. Указываю
номера страниц учебника, где можно найти соответствующее правило, определение и
пр. Осуществляю подбор упражнений и распределяю их на классную и домашнюю
работу. Отражаю вид доски и последовательность появления записей. Продумываю и
фиксирую обратную связь. Указываю, что заранее должно быть записано на доске.
Строю опорный конспект темы. Фиксирую методические находки, дату изучения затем,
чтобы сравнить с повторным прохождением темы. Дифференцирую материал по классам
и ученикам. Для меня план – место записей на уроке».
Как видно из ответов
учителей, они большую роль отводят математическому содержанию урока. При
личностно ориентированном обучении важно фиксировать то, что обогащает опыт
учащихся; те приемы, которые выводят учащихся на позиции субъектов обучения и
собственного развития; удачные варианты мотивации материала, задания, той или
иной записи, а также деятельности учащихся; общие вопросов диалога, которые
можно отнести в копилку не только учителя, но и учащихся; цели и подведение
итогов по процессу их достижения.
Так, при
изучении теоремы о плоскости, проходящей через прямую и не лежащую на ней точку
важно зафиксировать: 1) вопрос, мотивирующий изучение теоремы («В аксиомах
рассматривается один способ задания плоскости. Можно ли задать плоскость
иначе?»); 2) вопрос, демонстрирующий общий подход к заданию плоскости («Можно
ли провести плоскость, зная другие ее элементы?»); 3) суть метода воображаемого
построения («Выделяется такая цепочка логических рассуждений, которые
обосновывают возможность каждого шага построения»); 4) выделение в теореме двух
частей (существование и единственность); 5) вопросы диалога по поиску путей
построения («Начнем рассуждать с последнего шага. Какие фигуры к этому моменту
надо иметь? Имеем ли? Можем ли построить? Почему?»); 6) отражение
последовательности поиска на чертеже; 7) вопросы по подведению итогов этапу
построения («Удовлетворяет ли построенная плоскость заданным условиям? Каким
методом проводили доказательство? Что надо помнить при проведении доказательства
этим методом?»); 8) мотивацию необходимости доказательства единственности
(«Проанализируем каждый шаг построения и подумаем, единственным ли образом он
выполняется, чтобы знать, нужно ли доказывать единственность или она следует из
построения»); 9) мотивацию методу доказательства единственности
(«Единственность в большинстве случаев доказывается методом от противного»);
10) прием, который помогает поиску решения или доказательства в стереометрии
(«Как только появляется новая фигура, рассматривают ее взаимное расположение с
другими фигурами. По предположению у нас появилась новая плоскость, рассмотрим
ее взаимное расположение с построенной плоскостью. Что известно о новой
плоскости?...»); 11) оформление доказательства каждой части теоремы.
В завершении
первого дня занятий учителя конструировали фрагменты введения и усвоения
конкретной теоремы (работа в группах). На группы слушатели были разбиты
на предыдущем занятии и соответственно готовили дома работу с теоремами:
·
объем
пирамиды (учебник Л.С.Атанасяна);
· разложение
вектора по двум неколлинеарным векторам (учебник Л.С.Атанасяна);
· признак
параллельности прямых в пространстве (учебник А.В.Погорелова);
План
работы во второй
день:
- Представление фрагментов уроков группами.
- Компьютерные презентации теорем.
- Подведение итогов, постановка домашнего задания,
подготовка к педагогической мастерской.
Дадим
комментарий содержанию второго дня занятия.
Начался день с представления
фрагментов уроков группами. Рассмотрим предложенные группами варианты и
дополним их.
Объем
пирамиды.
1. Мотивация целей урока и актуализация
знаний.
Сегодня выведем
еще одну формулу, позволяющую вычислять объемы – формулу для вычисления объема
пирамиды. Какой математический аппарат позволит вывести эту формулу (Объем
можно вычислить с помощью формулы: V = 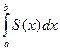 ). Что надо знать, чтобы воспользоваться этой формулой
(надо убедиться, что тело заключено между параллельными плоскостями; определить
числа a и b; выразить площадь поперечного
сечения через данные величины). К какому телу мы применяли эту формулу? (К
вычислению объема призмы). Напомните этапы изучения теоремы об объеме призмы
(Сначала рассмотрели треугольную призму и для вычисления ее объема применили
интеграл; затем рассматривали произвольную призму, для вычисления ее объема мы
разбивали призму на треугольные). Почему мы не стали сразу рассматривать
произвольную призму? (Если бы мы сразу рассматривали произвольную призму, нам
бы пришлось доказывать равенство основания призмы поперечному сечению, а
признаков равенства произвольных многоугольников мы не знаем). Наметьте план
изучения объема пирамиды (Сначала рассмотреть треугольную пирамиду и для
вычисления ее объема применить интеграл; затем рассмотреть произвольную
пирамиду, для вычисления ее объема разбить пирамиду на треугольные).
). Что надо знать, чтобы воспользоваться этой формулой
(надо убедиться, что тело заключено между параллельными плоскостями; определить
числа a и b; выразить площадь поперечного
сечения через данные величины). К какому телу мы применяли эту формулу? (К
вычислению объема призмы). Напомните этапы изучения теоремы об объеме призмы
(Сначала рассмотрели треугольную призму и для вычисления ее объема применили
интеграл; затем рассматривали произвольную призму, для вычисления ее объема мы
разбивали призму на треугольные). Почему мы не стали сразу рассматривать
произвольную призму? (Если бы мы сразу рассматривали произвольную призму, нам
бы пришлось доказывать равенство основания призмы поперечному сечению, а
признаков равенства произвольных многоугольников мы не знаем). Наметьте план
изучения объема пирамиды (Сначала рассмотреть треугольную пирамиду и для
вычисления ее объема применить интеграл; затем рассмотреть произвольную
пирамиду, для вычисления ее объема разбить пирамиду на треугольные).
2. Формулировка задачи вычисления объема
треугольной пирамиды и ее решение.
Задача:
вычислить объем треугольной пирамиды, зная площадь основания S и ее высоту h.
Учащиеся
выделяют условие задачи и ее заключение, делают чертеж. Далее формулируют
каждый шаг алгоритма вычисления объема с помощью интеграла и применяют его для
вычисления объема треугольной пирамиды.
Алгоритм:
1)
проверить, можно ли для данного тела использовать
интеграл (тело должно быть заключено между двумя параллельными плоскостями);
2)
выбрать ось абсцисс (выбрать начало отсчета и
направление; ось должна быть перпендикулярна плоскостям, между которыми
находится тело);
3)
определить числа а
и b – границы изменения х;
4)
выбрать произвольное х между числами а и b; через него провести
плоскость, перпендикулярную оси абсцисс, и выразить площадь полученного сечения
через данные величины;
5)
применить формулу вычисления объема с помощью
интеграла.
3. Подведение итогов и оформление полученных
результатов в виде первой части теоремы.
4. Вывод формулы вычисления объема
произвольной пирамиды (самостоятельная работа учащихся).
5. Решение задач на непосредственное
применение теоремы.
1)
Что надо знать, чтобы найти объем пирамиды по
выведенной формуле? Сформулируйте свои задачи.
2)
Сформулируйте обратные задачи. Как они решаются?
Дополнение к выступлению группы.
Учителя предложили вариант, когда
формулу учащиеся выводят вместе с учителем в рамках математической задачи.
Возможны иные варианты:
- Учащиеся самостоятельно применяют алгоритм к
вычислению объема треугольной пирамиды, после того, как вывели на прошлом
уроке формулу вычисления объема призмы (варианты: по группам, один у
доски, индивидуально; выбор начала оси абсцисс и направления вариативен).
- Две теоремы (объем треугольной призмы и объем
треугольной пирамиды) изучаются одновременно.
- Учащиеся работают с учебником и оформляют
доказательство теоремы.
Учителя предложили факт, что
сечение треугольной пирамиды плоскостью, параллельной основанию, подобно
основанию с коэффициентом, равным отношению расстояния от вершины пирамиды до
сечения к высоте пирамиды, рассматривать в рамках теоремы. Возможен вариант,
что указанный факт рассматривается в виде опорной задачи в теме «Пирамида».
Разложение
вектора по двум неколлинеарным векторам (учебник Л.С.Атанасяна).
Учителя
рассматривали указанную теорему, исходя из того, что лемму о коллинеарных
векторах и понятие разложения вектора изучили на предыдущем уроке.
1. Актуализация знаний и мотивация теоремы.
Сегодня мы продолжим работу с векторами
и решим следующую задачу. На доске изображен параллелограмм АВСД, точка М – середина стороны АВ,
точка Q – середина стороны АД,
точка О – точка пересечения
диагоналей. 1) Выразите вектор АС
через вектора АВ и АД; 2) вектор АС – через вектора АМ и АQ; 3) вектор ВД – через вектора ВМ и АД; 4) вектор ВС – через вектора ВД и ВМ; 5) вектор ДВ через вектора ДО и ДА.
Если учащиеся легко справляются с
этим заданием, то учитель предлагает им проанализировать, что общего было в
условии заданий, что общего в заключении, как сформулировать полученные выводы
в виде математического утверждения (формулируется теорема о возможности
разложения вектора по двум неколлинеарным векторам). Если учащиеся затруднятся
в каком-нибудь примере, то учитель поставит проблему: «Может быть, в этих
примерах задача не имеет решений?». Затем предложит применить общий для
математики метод – метод дедукции: сформулировать утверждение в общем виде и
попробовать его доказать или опровергнуть.
2. Доказательство существования разложения
вектора по двум неколлинеарным векторам.
По составленному с учащимися
условию (даны два неколлинеарных вектора a и b и
произвольный вектор р)
выполняют самостоятельно чертеж. Хорошо, если получится, что кто-то из учащихся
возьмет вектор р,
коллинеарным одному из данных; кто-то возьмет все три вектора, выходящими из
одной точки. На всякий случай, учитель заранее на обороте доски делает свои
чертежи. Сначала обсуждается выбор чертежа: «Принципиально ли, что у кого-то
векторы не выходят из одной точки?». Все другие расположения вектора р учащиеся
разбивают на три случая: коллинеарен вектору а, коллинеарен
вектору b, не коллинеарен
ни одному из данных векторов (позднее, учащиеся объединят первые два случая в
один, т.к. они имеют единое доказательство).
Обсуждается суть поставленной
задачи о возможности разложения вектора по двум неколлинеарным векторам: надо
найти такие числа х
и у, чтобы выполнялось равенство 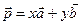 .
.
Учащиеся анализируют выделенные
случаи и предлагают свои варианты поиска коэффициентов х и у. Если задача вызывает у них затруднения, то возвращаются к
заданиям этапа актуализации и выясняют, почему они были успешными в тех или
иных примерах. Так возникает идея о введении векторов, чья сумма равна вектору р. Осталось выразить построенные векторы
через данные векторы а и b.
3. Доказательство единственности разложения.
Мотивируется эта часть
доказательства тем, что в математике часто доказывают не только то, что можно
решить задачу (в нашем случае, что существуют такие числа х и у), но и выясняют, сколько решений имеет задача. Так возникает
формулировка о единственности разложения вектора по двум неколлинеарным
векторам.
Поскольку единственность в
большинстве случаев доказывается методом от противного, для доказательства этой
части теоремы применяется этот метод. Итак, пусть есть два разложения вектора р:
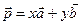 и
и 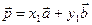 .
.
Имея два
равенства, можно выполнить операции над ними. Имея два равенства с одинаковыми
левыми частями, можно приравнять правые части. Какие новые равенства можно
получить? Учащиеся составляют новое равенство, используя операцию вычитания,
или приравнивая правые части. Дальнейший анализ о том, когда сумма двух
ненулевых векторов равна нулю (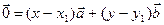 ), приводит к выделению ситуаций: 1) оба коэффициента равны
0; 2) один из коэффициентов отличен от нуля (например, х – х1), тогда вектор b можно выразить через
вектор а, что противоречит условию,
что данные векторы не являются коллинеарными. Таким образом, из двух ситуаций
остается первая: х – х1 = 0, у – у1= 0, значит, х = х1 и у = у1.
), приводит к выделению ситуаций: 1) оба коэффициента равны
0; 2) один из коэффициентов отличен от нуля (например, х – х1), тогда вектор b можно выразить через
вектор а, что противоречит условию,
что данные векторы не являются коллинеарными. Таким образом, из двух ситуаций
остается первая: х – х1 = 0, у – у1= 0, значит, х = х1 и у = у1.
В дополнение к
выступлению учителей им были даны материалы статьи «Обобщение и систематизация
при изучении теоремы», подготовленной в рамках дипломного проектирования
студентов, а также рекомендации по изучению разложения вектора по двум
неколлинеарным векторам по учебнику А.В.Погорелова.
Т.В.Акимов, И.Е.Малова
Обобщение и систематизация при
изучении теорем
Для полноценного усвоения математической
деятельности, связанной с доказательствами теорем важно проводить обобщение и
систематизацию тех приёмов и методов, с помощью которых осуществляются
доказательства. Без этого мы не получаем стройную математическую структуру, в
которой все звенья взаимосвязаны, а получаем нагромождение большого количества фактов,
несвязанных приёмов и методов, которыми ребёнок не в состоянии воспользоваться
для самостоятельных открытий. В стороне от обучаемого не должен остаться «сам
процесс познания, методы и способы получения субъективно необходимых для
ученика знаний» [1, С.23].
«Предмет и методика математики, её ведущие
идеи и понятия, математический язык, связь с другими науками и практикой,
математическое моделирование; процесс познания в математике; специфика
творческой математической деятельности как сплав индукции и логики; методы
научного познания (как общие: эвристические и логические, так и специфические
способы и приёмы); эстетика математики; культура мышления; история математики
составляют гуманитарный потенциал предмета» [1, С.26]. Чтобы потенциал так и не
остался потенциалом, а интегрировался в опыт учащихся, важно, обобщая и систематизируя
изученное, обращать внимание на гуманитарную составляющую математики. Во время
урока, когда начинают рассматриваться глубинные аспекты человеческого мышления,
когда ребята начинают спрашивать себя: «А почему я решил так, а не иначе», «А почему эта
теорема доказывается тем, а не иным способом?», «А почему…?», этих «А почему?»
и ответов на них набирается столь обширное количество, что происходит существенное
обогащение опыта учащихся, а значит, и их математическое развитие. Чтобы накопление
опыта происходило, очень важно по мере изучения предмета обобщать и систематизировать
все аспекты, относящиеся к гуманитарной составляющей математики. Происходит
закрепляющий этап, который подводит черту на изученном и даёт необходимые предпосылки
для постижения нового. Как итог, мы получаем, что по прошествии некоторого
времени ребёнок будет самостоятельно решать задачи, открывать и доказывать некоторые
теоремы, а не механически переписывать формулировки и доказательства, воспринимая
это как какую-то аксиоматическую структуру. Он будет думать, развиваться, использовать
те правила и методы, с помощью которых обнародовались новые факты, доказывались
известные ему теоремы, леммы, следствия. Это как раз и соотносится с одной из
задач современной школы: воспитать человека мыслящего, с гуманитарным
внутренним содержанием, способного на дальнейшее развитие.
Новейшие тенденции в современном образовании
важно соотносить с изучаемым предметным контекстом. Рассмотрим некоторые
правила и методы, которые можно вынести на обсуждение при обобщении и
систематизации работы с двумя теоремами в теме «Векторы».
Теорема 1: Пусть 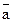 ,
,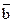 – отличные от нуля
коллинеарные вектора, докажем, что существует
– отличные от нуля
коллинеарные вектора, докажем, что существует 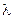 такое, что
такое, что 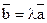 .
.
Определим место теоремы в системе старых
знаний, т.е. найдем тот материал, оттолкнувшись от которого учащиеся смогут
прийти к формулировке теоремы. Таким материалом может быть геометрическое нахождение
произведения вектора на число. Выполнив вычисление произведений одного и того
же вектора на разные числа, проанализировав полученные изображения, учащиеся приходят
к выводу, что везде получаются коллинеарные векторы. Далее ставится обратная задача:
«Пусть даны коллинеарные векторы. Что можно найти по этим данным?». Через этот
путь учащиеся приходят к формулировке теоремы. Доказательство данной теоремы
проводится методом полной индукции. Он заключается в рассмотрении всех случаев
расположения векторов: одинаково и противоположно направленные вектора.
На этапе усвоения рассмотренной теоремы
важно возвратиться к двум методам: методу обнаружения новых фактов (поставь
обратную задачу), методу доказательства (методу полной индукции), ещё раз проанализировать
процесс использования этих методов.
Теорема 2: Любой вектор 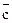 можно представить в
виде:
можно представить в
виде: 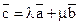 , где
, где 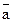 ,
,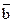 – неколлинеарные
векторы,
– неколлинеарные
векторы, 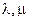 – какие-то фиксированные
константы, причём коэффициенты разложения определяются единственным образом.
– какие-то фиксированные
константы, причём коэффициенты разложения определяются единственным образом.
Использование рассмотренного метода обнаружения новых фактов на анализе
примера нахождения суммы двух неколлинеарных векторов, приводит к выводу, что
один вектор может выражаться через два других. Варьирование расположения
данного вектора приводит к гипотезе не только вывода, сформулированного в
теореме, но и к способу доказательства. На этапе усвоения этот новый приём (варьирования)
оговаривается.
1.
Теоретические основы обучения математике в средней школе: Учебное пособие
/Т.А.Иванова, Е.Н.Перевощикова, Т.П.Григорьева,
Л.И.Кузнецова; Под ред. Т.А.Ивановой. – Н.Новгород: НГПУ, 2003. – 320 с.
Теорема о разложении вектора по
двум неколлинеарным векторам (учебник А.В.Погорелова).
Введение формулировки свойства коллинеарных векторов:
1)
практическая работа по геометрическому умножению
вектора на числа:
2, -2, 1,5; ¾, (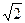 );
);
2)
формулирование вывода об особенностях всех построенных
векторов;
3)
постановка обратной задачи: даны два коллинеарных
вектора, требуется определить число, на которое надо умножить один из них,
чтобы получить второй;
4)
выдвижение гипотез по поиску такого числа; можно
провести экспериментальную работу по подбору такого числа; гипотеза содержит
три вывода: а) число может быть положительным (если данные вектора сонаправлены), отрицательным (если данные вектора противоположно
направлены); б) модуль числа равен отношению модулей длин векторов; в) такое
число всегда можно подобрать;
5)
формулирование теоремы (леммы) и составление плана
доказательства.
Оформление
доказательства:
Формулирование выводов по изученной теореме:
1) что
помогло нам сформулировать теорему? (поставили
обратную задачу);
2)
что помогло
обнаружить способ доказательства? (экспериментирование с векторами) (в
математике такой подход называют индуктивным);
3)
сколько
случаев рассмотрели и почему их достаточно? (мы рассмотрели два случая
коллинеарных векторов, других случаев не бывает) (в математике метод, когда рассмотрены
все частные случаи, называют методом полной индукции).
Введение формулировки теоремы о разложении вектора по двум
неколлинеарным:
1)
попробуем обнаружить новый математический факт,
используя индукцию и постановку обратной задачи; поработаем с неколлинеарными
векторами: что учились делать с такими векторами? (складывать, находить скалярное
произведение);
2)
возьмите два неколлинеарных вектора и выполните их
сложение; запишите полученный результат (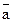 +
+ 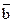 =
= 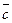 );
);
3) попробуем поставить обратные задачи
(выслушиваются формулировки и возможности решения задач);
4)
учитель предлагает свою обратную задачу: даны векторы 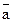 ,
, 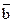 ,
, 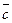 ; найти коэффициенты
; найти коэффициенты 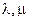 , чтобы выполнялось равенство:
, чтобы выполнялось равенство: 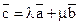 , где
, где 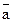 и
и 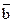 - неколлинеарные
векторы; для исходной задачи учащиеся называют
- неколлинеарные
векторы; для исходной задачи учащиеся называют 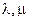 ;
;
5)
экспериментирование с произвольным вектором 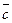 и постановка задачи о
возможности определения чисел
и постановка задачи о
возможности определения чисел 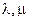 (хорошо, если найдутся
учащиеся, которые вектор
(хорошо, если найдутся
учащиеся, которые вектор 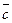 возьмут коллинеарным
одному из данных; если таких не будет, то после обсуждения планов
доказательства (пункт 7) посмотреть доказательство в учебнике);
возьмут коллинеарным
одному из данных; если таких не будет, то после обсуждения планов
доказательства (пункт 7) посмотреть доказательство в учебнике);
6) формулирование первой части теоремы (о
существовании) и выдвижение гипотезы о единственности;
7)
формулирование теоремы и обсуждение планов
доказательства.
Формулирование выводов по изученной теореме:
1)
что помогло нам сформулировать теорему? (поставили обратную задачу);
2)
что помогло
обнаружить способ доказательства? (экспериментирование с векторами) (Как в математике
называют такой подход?);
3)
сколько
случаев рассмотрели и почему их достаточно? (мы рассмотрели два случая: вектор 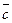 коллинеарен или нет одному из данных векторов, других
случаев не бывает) (Как в математике называют метод, когда рассмотрены все частные
случаи?);
коллинеарен или нет одному из данных векторов, других
случаев не бывает) (Как в математике называют метод, когда рассмотрены все частные
случаи?);
4)
можно ли было
ограничиться одним из рассмотренных случаев? Почему нельзя?
Теорема
– признак параллельности прямых в пространстве (учебник А.В.Погорелова) вызвала затруднения у учителей. Поэтому
было предложено самостоятельно вернуться к теореме, используя следующие
методические рекомендации.
При
доказательстве этой теоремы удобно использовать ряд методических и математических
приемов:
·
(Прием дополнительной плоскости) Для
доказательства теорем и решения задач часто помогает дополнительное построение
плоскости; какие данные позволяют построить плоскости? (Строятся плоскость
β через параллельные прямые а и b и плоскость γ через
параллельные прямые а и с).
·
(Метод анализа) В теореме требуется доказать,
что прямые b и с параллельны. Что это значит?
Это значит, что эти прямые лежат в одной плоскости и не пересекаются.
·
(Прием доказательства, что фигура, построенная
по самостоятельно выбранным условиям, удовлетворяет данным условиям) В
математике часто используется прием, когда по некоторым данным строится
дополнительная плоскость, а потом доказывается, что построенная плоскость
удовлетворяет требуемым условиям. Применительно к рассматриваемой теореме,
строится плоскость γ1 через прямую с и точку В, выбранную на прямой b. Что
останется доказать?
·
(Прием рассмотрения взаимного расположения
фигур) Как только возникает новая фигура определяют ее взаимное расположение с
другими имеющимися фигурами. Плоскости β и γ1 имеют общую
точку В, значит, они пересекаются по прямой, проходящей через эту точку. Мы не
может утверждать, что это прямая b, поэтому пусть это
будет прямая b1. Возникла новая фигура
(прямая b1), значит, важно
определить ее взаимное расположение с другими имеющимися фигурами. Начинают со
взаимного расположения прямой b1 и плоскости
γ.
·
(метод от противного) Если b1 пересекает
плоскость γ, то она пересекает прямую а
(если прямая, лежащая в одной из пересекающихся плоскостей, пересекает другую
плоскость, то она пересекает линию пересечения плоскостей). По той же причине,
если b1 пересекает плоскость γ, то она пересекает
прямую с. Поскольку прямая, не
лежащая в плоскости, может пересекать плоскость в единственной точке, а по
доказанному она лежит как на прямой а,
так и на прямой с, значит, прямые а и с
пересекаются, что противоречит условию. Поэтому прямая b1 и
плоскости γ не пересекаются.
·
(метод синтеза) Если прямая и плоскость не
пересекаются, то какие выводы можно сделать? (эта прямая не пересекает любую
прямую, лежащую в этой плоскости). Значит, каково взаимное расположение прямых b1 и а; b1 и с?
Прямые b1 и а
лежат в одной плоскости (плоскости β) и не пересекаются, значит, они
параллельны (тогда совпадают прямые b1 и b). Прямые b1 и с лежат в одной плоскости (плоскости
γ1) и не пересекаются, значит, они параллельны, а поскольку b1 и b совпадают, прямые b1 и с
параллельны, что и требовалось доказать.
К занятию были
подготовлены компьютерные презентации: изучение площади сферы (учитель Н.В.Фролова); изучение
объема пирамиды по учебнику А.В.Погорелова (аспирантка И.А.Котова).
К занятию № 7 было предложено выполнить
следующее домашнее задание:
1) выполнить
контрольную работу № 3: представить копию планов двух последовательных уроков,
отраженных в рабочих тетрадях учителя;
2) вернуться к анкете по
методике изучения теорем и исправить обнаруженные ошибки;
3) провести самоанкетирование по методике обучения учащихся решению
текстовых задач (по методическому пособию «Система профессиональной подготовки
учителя старшей школы…»);
4) в рамках подготовки к
педагогической мастерской по проблеме «Личность. Математика. Выбор профессии»
предложить учащимся выполнить следующие творческие задания: выяснить, какие
задачи приходится решать в выбранных ими профессиях; какие умения требуются,
чтобы быть успешными в выбранных профессиях.