СОДЕРЖАНИЕ
Задание
1. 2
Задание
2. 8
Задание
3. 11
Задание
4. 14
Задание
5. 17
СПИСОК
ЛИТЕРАТУРЫ.. 19
ВАРИАНТ
7
Задание 1
Для выявления зависимости между экономическими показателями деятельности
фирм провести группировку показателей 50 аудиторских фирм (см. табл.1).
Группировку провести с равными интервалами, выделив 4 или 5 групп. Результативный
признак – балансовая прибыль, группировочный признак – нематериальные активы.
Предприятия 7 – 56.
Таблица 1
Основные
показатели деятельности аудиторских фирм за период «N»
|
№ п/п
|
Балансовая прибыль,
р. (у)
|
Нематериальные
активы, руб. (х)
|
№ п/п
|
Балансовая прибыль,
р. (у)
|
Нематериальные
активы, руб. (х)
|
|
7
|
22446
|
0
|
32
|
37133
|
19700
|
|
8
|
71
|
0
|
33
|
31500
|
20600
|
|
9
|
40
|
31
|
34
|
36100
|
17840
|
|
10
|
37416
|
7438
|
35
|
1200
|
11457
|
|
11
|
4100
|
0
|
36
|
5000
|
13400
|
|
12
|
1116
|
6375
|
37
|
19148
|
8100
|
|
13
|
0
|
1067
|
38
|
13200
|
7939
|
|
14
|
4957
|
0
|
39
|
3610
|
5620
|
|
15
|
9838
|
10631
|
40
|
12500
|
6532
|
|
16
|
632
|
406
|
41
|
18451
|
11470
|
|
17
|
14453
|
3100
|
42
|
5600
|
24586
|
|
18
|
50890
|
2419
|
43
|
12735
|
21258
|
|
19
|
32117
|
5746
|
44
|
10540
|
18726
|
|
20
|
24541
|
7428
|
45
|
30900
|
23775
|
|
21
|
3244
|
5846
|
46
|
40000
|
17160
|
|
22
|
2870
|
19665
|
47
|
6541
|
4170
|
|
23
|
11309
|
7752
|
48
|
8900
|
3560
|
|
24
|
38654
|
15755
|
49
|
2156
|
6500
|
|
25
|
48400
|
20431
|
50
|
45820
|
25120
|
|
26
|
19120
|
10356
|
51
|
550
|
1500
|
|
27
|
15545
|
9300
|
52
|
3450
|
3750
|
|
28
|
7400
|
4735
|
53
|
6114
|
3600
|
|
29
|
6372
|
3800
|
54
|
2777
|
5020
|
|
30
|
8100
|
5136
|
55
|
130
|
186
|
|
31
|
20950
|
17210
|
56
|
1445
|
4807
|
Рассчитать коэффициенты вариации по группировочному признаку на основании
исходных данных и по аналитической группировке, согласно своему варианту.
Объяснить расхождения в значениях полученных коэффициентов.
Решение
Группировка является основой научной сводки и обработки статистических
данных. Группировочный признак в нашем примере – нематериальные активы,
результативный признак – балансовая прибыль. Количество групп принимаем – 5
групп.
Необходимо определить интервалы группировки и их величины.
Величина интервала определяется по формуле:
d = 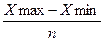 ,
(1)
,
(1)
где хmax
– максимальное значение количественного признака;
xmin – минимальное значение
количественного признака;
n – число намечаемых групп.
Величина интервала составит:
d = 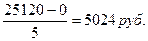
Верхняя граница предыдущей группы совпадает с нижней границей последующей
группы.
После определения границ
интервалов составим рабочую таблицу (табл. 2), в которую сведем первичный
статистический материал.
Таблица 2
Рабочая
таблица
|
Номер группы
|
Граница
|
|
Нижняя
|
Верхняя
|
|
1
|
0
|
5024
|
|
2
|
5024
|
10048
|
|
3
|
10048
|
15072
|
|
4
|
15072
|
20096
|
|
5
|
20096
|
25120
|
Результаты группировки оформим в виде табл. 3.
Таблица 3
Группировка
аудиторских фирм по стоимости нематериальных активов
|
Группы предприятий по стоимости нематериаль-ных
активов
|
Число предприятий в группе
|
Номер предприя-тия
|
Нематериальные активы, руб.
|
Балансовая прибыль, руб.
|
|
Всего по группе
|
В среднем на одно предприятие
|
Всего по группе
|
В среднем на одно предприятие
|
|
0 – 5024
|
19
|
7,8,9,11,13,14,16,17,18,28,29,47,48,51,52,53,54,55,56
|
42151
|
2218,5
|
141268
|
7435,1
|
|
5024 – 10048
|
13
|
10,12,19,20,21,23,27,30,37,38,39,40,49
|
89712
|
6900,9
|
184002
|
14154
|
|
10048 – 15072
|
5
|
15,26,35,36,41
|
57314
|
11462,8
|
53609
|
10721,8
|
|
15072 – 20096
|
7
|
22,24,31,32,34,44,46
|
126056
|
18008
|
186247
|
26606,7
|
|
20096 – 25120
|
6
|
25,33,42,43,45
|
136040
|
22673,3
|
174955
|
29159,2
|
|
ИТОГО:
|
50
|
−
|
451273
|
−
|
740081
|
−
|
Изучив данные 50-ти предприятий о стоимости нематериальных активов и
величине балансовой прибыли, можно сказать, что связь между этими показателями
слабая или отсутствует, так как величина балансовой прибыли меняется независимо
от роста нематериальных активов.
Величина вариации признака в статистической совокупности характеризует
степень ее однородности, что имеет большое практическое значение.
Относительным показателем уровня вариации признака является коэффициент
вариации. Он представляет собой отношение среднего квадратического отклонения к
средней величине признака и выражается обычно в процентах:
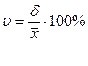 (2)
(2)
где δ – среднее квадратическое отклонение;
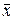 – средняя величина.
– средняя величина.
Если коэффициент вариации больше 33%, то совокупность неоднородна и ее
средняя нетипична.
Расчет средней величины произведем по средней арифметической простой (при
расчете по исходным данным) и по средней арифметической взвешенной (при расчете
по аналитической таблице).
Формулы для расчета средних величин в зависимости от исходных данных:
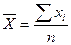 ,
(3)
,
(3)
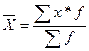 ,
(4)
,
(4)
где n – численность совокупности;
хi – варианта или
значение признака;
f – частота повторения индивидуального
значения признака (его вес).
Среднее квадратическое отклонение показывает на сколько в среднем
колеблется величина признака у единиц исследуемой совокупности и определяется в
зависимости от характера исходных данных.
При расчете по исходным данным
используем формулу:
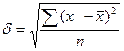 (5)
(5)
По сгруппированным данным:
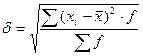 (6)
(6)
Сначала рассчитаем показатели вариации для данных предприятий по исходным
данным. Для этого составим таблицу 4.
Таблица
4
Расчет
показателей вариации по исходным данным о стоимости нематериальных активов
|
№ п/п
|
Нематериальные активы (х), тыс.р.
|
х-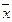 , тыс.р. , тыс.р.
|
(х-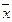 )2,
тыс. р )2,
тыс. р
|
№ п/п
|
Нематериальные активы (х), тыс.р.
|
х-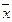 , тыс.р. , тыс.р.
|
(х-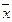 )2,
тыс. р )2,
тыс. р
|
|
7
|
0
|
-9,02
|
81,36
|
32
|
19,700
|
10,68
|
114,06
|
|
8
|
0
|
-9,02
|
81,36
|
33
|
20,600
|
11,58
|
134,10
|
|
9
|
0,031
|
-9,0
|
81,00
|
34
|
17,840
|
8,82
|
77,79
|
|
10
|
7,438
|
-1,58
|
2,50
|
35
|
11,457
|
2,437
|
5,94
|
|
11
|
0
|
-9,02
|
81,36
|
36
|
13,400
|
4,38
|
19,18
|
|
12
|
6,375
|
-2,645
|
7,00
|
37
|
8,100
|
-0,92
|
0,85
|
|
13
|
1,067
|
-7,953
|
63,25
|
38
|
7,939
|
-1,081
|
1,17
|
|
14
|
0
|
-9,02
|
81,36
|
39
|
5,620
|
-3,4
|
11,56
|
|
15
|
10,631
|
1,611
|
2,59
|
40
|
6,532
|
-2,488
|
6,19
|
|
16
|
0,406
|
8,614
|
74,20
|
41
|
11,470
|
2,45
|
6,00
|
|
17
|
3,100
|
5,92
|
35,05
|
42
|
24,586
|
15,566
|
242,30
|
|
18
|
2,419
|
-6,601
|
43,57
|
43
|
21,258
|
12,238
|
149,77
|
|
19
|
5,746
|
-3,274
|
10,72
|
44
|
18,726
|
9,706
|
94,21
|
|
20
|
7,428
|
-1,592
|
2,53
|
45
|
23,775
|
14,755
|
217,71
|
|
21
|
5,846
|
-3,174
|
10,07
|
46
|
17,160
|
8,14
|
66,26
|
|
22
|
19,665
|
10,645
|
113,32
|
47
|
4,170
|
-4,85
|
23,52
|
|
23
|
7,752
|
1,268
|
1,61
|
48
|
3,560
|
-5,46
|
29,81
|
|
24
|
15,755
|
6,735
|
45,36
|
49
|
6,500
|
-2,52
|
6,35
|
|
25
|
20,431
|
11,411
|
130,21
|
50
|
25,120
|
16,1
|
259,21
|
|
26
|
10,356
|
1,336
|
1,78
|
51
|
1,500
|
-7,52
|
56,55
|
|
27
|
9,300
|
0,28
|
0,08
|
52
|
3,750
|
-5,27
|
27,77
|
|
28
|
4,735
|
-4,285
|
18,36
|
53
|
3,600
|
-5,42
|
29,38
|
|
29
|
3,800
|
-5,22
|
27,25
|
54
|
5,020
|
-4,0
|
16,00
|
|
30
|
5,136
|
-3,884
|
15,08
|
55
|
0,186
|
-8,834
|
78,04
|
|
31
|
17,210
|
8,19
|
67,08
|
56
|
4,807
|
-4,213
|
17,75
|
|
Итого:
|
50
|
451,273
|
−
|
2769,52
|
Средняя по исходным данным, тыс. руб.:
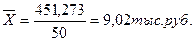
Среднее квадратическое отклонение по исходным данным, тыс. руб.:
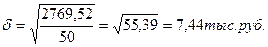
Коэффициент вариации по исходным данным, % :
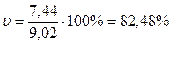
Рассчитаем показатели вариации по сгруппированным данным. Для расчетов
составим таблицу 5.
Таблица
5
Расчет
показателей вариации по сгруппированным данным по стоимости нематериальных
активов
|
Группы предприятий по стоимости нематериальных
активов, р.
|
Количество предприятий
f
|
Расчетные показатели
|
|
Середина интервала  , тыс. р. , тыс. р.
|
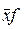 , тыс.р. , тыс.р.
|
х-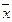 , тыс.р. , тыс.р.
|
(х-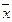 )2f, тыс. р. )2f, тыс. р.
|
|
0 – 5024
|
19
|
2,512
|
47,73
|
-6,828
|
885,81
|
|
5024 – 10048
|
13
|
7,536
|
97,97
|
-1,804
|
42,31
|
|
10048 – 15072
|
5
|
12,560
|
62,8
|
3,22
|
51,84
|
|
15072 – 20096
|
7
|
17,584
|
123,09
|
8,244
|
475,74
|
|
20096 – 25120
|
6
|
22,608
|
135,65
|
13,268
|
1056,24
|
|
ИТОГО:
|
50
|
−
|
467,24
|
−
|
2511,94
|
Средняя величина по сгруппированным данным, тыс. руб.:
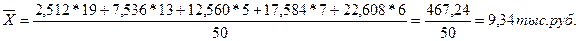
Среднее квадратическое отклонение по
сгруппированным данным, тыс. руб.:
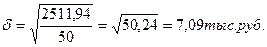
Коэффициент вариации по сгруппированным данным, %:
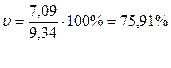
В обоих расчетах коэффициент вариации значительно больше 33%. Следовательно,
рассмотренная совокупность неоднородна и средняя для нее недостаточно типична.
Задание 2
Провести 30 % механическую выборку из генеральной совокупности,
представленной в табл. 1, по показателю, который является для Вашего варианта
результативным. С вероятностью 0,95 рассчитать границы изменения средней
величины в генеральной совокупности (по табл.1) и сравнить с результатом,
полученным на основании расчета по выборочной совокупности. Отбор начинать с
номера предприятия, который совпадает с номером Вашего варианта.
Решение
Выборочное наблюдение представляет собой один из наиболее широко
применяемых видов несплошного наблюдения.
Система правил отбора единиц и способов характеристики изучаемой
совокупности исследуемых единиц составляет содержание выборочного метода.
Механическая выборка предполагает, что отбор единиц генеральной
совокупности производится через равные промежутки, то есть через определенное
число единиц.
Отбор предприятия начинаем с предприятия № 7 (вариант 7).
При 30 % выборке в выборочную совокупность должно попасть 18 фирм.
Таблица исходных данных выборочной совокупности выглядит следующим
образом: (см.табл. 6).
Таблица 6
Исходные
данные выборочной совокупности
|
Номер предприятия
|
Балансовая прибыль,
руб.
|
Номер предприятия
|
Балансовая прибыль,
руб.
|
|
7
|
22446
|
34
|
36100
|
|
10
|
37416
|
37
|
19148
|
|
13
|
0
|
40
|
12500
|
|
16
|
632
|
43
|
12735
|
|
19
|
32117
|
46
|
40000
|
|
22
|
2870
|
49
|
2156
|
|
25
|
48400
|
52
|
3450
|
|
28
|
7400
|
55
|
130
|
|
31
|
20950
|
58
|
35800
|
|
ИТОГО:
|
18
|
334250
|
Величина случайной ошибки механического отбора определяется по упрощенной
формуле:
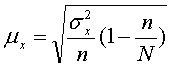 (7)
(7)
где N – объем генеральной совокупности,
(число входящих в нее единиц);
n – объем выборки, (число обследованных единиц);
δ2 – генеральная дисперсия
(дисперсия признака в генеральной совокупности).
Наиболее часто употребляемые уровни доверительной вероятности и соответствующие
значения коэффициента доверия t
для выборок достаточно большого объема:
|
t
|
1,00
|
1,96
|
2,00
|
2,58
|
3,00
|
|
Ф(t)
|
0,683
|
0,950
|
0,954
|
0,990
|
0,997
|
Значению вероятности 0,95 соответствует значение гарантийного
коэффициента, равное 1,96.
Для расчета границ изменения
средней характеристики генеральной совокупности по материалам выборки
воспользуемся следующими формулами:
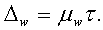 (8)
(8)
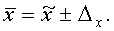 (9)
(9)
где

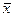 ─ средняя
генеральной совокупности;
─ средняя
генеральной совокупности;
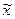 ─ средняя выборочной совокупности;
─ средняя выборочной совокупности;
Δх ─ предельная ошибка
выборки;
μх
─ средняя квадратическая ошибка выборки.
Средняя балансовая прибыль на одном предприятии равна, тыс. руб.:

Для расчета дисперсии признака
в генеральной совокупности составим таблицу 7.
Таблица 7
Расчет
показателей дисперсии признака в генеральной совокупности
|
№ фирмы
|
Балансовая прибыль,
тыс. руб.
|
х-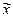 тыс. руб. тыс. руб.
|
(х-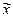 )2 тыс. руб. )2 тыс. руб.
|
|
7
|
22,446
|
3,877
|
15,03
|
|
10
|
37,416
|
18,847
|
355,21
|
|
13
|
0
|
-18,569
|
344,81
|
|
16
|
0,632
|
-17,937
|
321,73
|
|
19
|
32,117
|
13,548
|
183,55
|
|
22
|
2,870
|
-15,699
|
246,46
|
|
25
|
48,400
|
29,831
|
889,89
|
|
28
|
7,400
|
-11,169
|
124,75
|
|
31
|
20,950
|
2,381
|
5,67
|
|
34
|
36,100
|
17,441
|
304,19
|
|
37
|
19,148
|
0,579
|
0,33
|
|
40
|
12,500
|
-6,069
|
36,83
|
|
43
|
12,735
|
-5,834
|
34,03
|
|
46
|
40,000
|
21,431
|
523,58
|
|
49
|
2,156
|
-16,413
|
269,39
|
|
52
|
3,450
|
-15,119
|
228,58
|
|
55
|
0,130
|
-18,439
|
340,0
|
|
58
|
35,800
|
17,141
|
293,81
|
|
Итого:
|
334,25
|
─
|
4517,84
|
Дисперсия δ2 составит.:

Величина случайной ошибки:
μх = 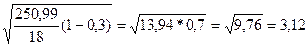
Рассчитаем предельную ошибку и определим границы изменения средней:
∆=1,96*3,12=6,11
18,569-6,11<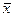 <18,569+6,11
<18,569+6,11
12,46<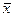 24,68
24,68
Таким образом, с вероятностью 0,95 можно утверждать, что балансовая
прибыль на одном предприятии в генеральной совокупности будет находиться в
пределах от 12,46 до 24,68 тыс. рублей.
Задание
3
По данным своего варианта (табл. 8) рассчитайте:
1) среднегодовой ввод жилых домов;
2) базисные, цепные и среднегодовые показатели абсолютного прироста,
темпов роста и темпов прироста ввода жилых домов;
3) изобразите динамику ввода жилых домов на графике.
Таблица 8
Данные
о вводе жилых домов строительной компании «N»
|
Номер варианта
|
Период, гг.
|
Год
|
Введено жилых
домов, тыс. м2 общей площади
|
|
1
|
1981-1990
|
1981
1982
|
23
26
|
|
2
|
1982-1991
|
1983
1984
|
27
29
|
|
3
|
1983-1992
|
1985
1986
|
30
33
|
|
4
|
1984-1993
|
1987
1988
|
35
37
|
|
5
|
1985-1994
|
1989
1990
|
42
46
|
|
6
|
1986-1995
|
1991
1992
|
48
48
|
|
7
|
1987-1996
|
1993
1994
|
50
50
|
|
8
|
1988-1997
|
1995
1996
|
51
52
|
|
9
|
1989-1998
|
1997
1998
|
52
54
|
|
10
|
1990-1999
|
1999
|
58
|
Решение
Абсолютный прирост (∆i) определяется как разность между двумя уровнями
динамического ряда. При сравнении с постоянной базой он равен:
∆i б =Yi – Y0, (10)
где ∆i б − абсолютный прирост базисный;
Yi −
уровень сравниваемого периода;
Y0 − уровень
базисного периода.
При сравнении с переменной базой абсолютный прирост равен:
∆i =Yi – Yi-1, (11)
где ∆i − абсолютный прирост
цепной;
Yi-1−
уровень непосредственно предшествующего периода.
Темп роста (Тр) определяется как отношение двух сравниваемых уровней.
При сравнении с постоянной базой:
Тр =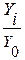 *100
% (12)
*100
% (12)
При сравнении с переменной базой:
Тр =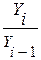 *100
% (13)
*100
% (13)
Темп прироста показывает на сколько процентов уровень данного периода
больше (или меньше) базисного уровня.
Тп =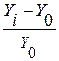 *100% или Тп =
*100% или Тп = 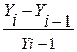 *100 %
*100 %
А также определяет разность между темпом роста (в %) и 100%:
Тп = Тр –
100% (14)
Средний уровень определяется по формуле:
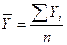 (14)
(14)
Средний абсолютный прирост рассчитывается по формуле:
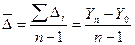 (15)
(15)
Среднегодовой темп роста определяется по среднегеометрической формуле:
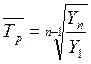 (16)
(16)
Среднегодовой темп прироста определяется по формуле:
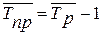 (17)
(17)
1) Среднегодовой ввод жилых домов определяем по формуле среднего уровня
ряда:
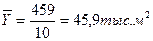
2) Рассчитаем все показатели по ряду динамики, характеризующему величину
ввода жилых домов. Данные расчета представим в таблице 9.
Таблица 9
Расчет
показателей динамики
|
Год
|
Ввод жилых домов,
тыс. м2
|
Абсолютный прирост
|
Темп роста, %
|
Темп прироста, %
|
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
|
1987
|
35
|
─
|
─
|
─
|
100
|
0,0
|
0,0
|
|
1988
|
37
|
2
|
2
|
105,71
|
105,71
|
5,71
|
5,71
|
|
1989
|
42
|
5
|
7
|
113,51
|
120,0
|
13,51
|
20,0
|
|
1990
|
46
|
4
|
11
|
109,52
|
131,43
|
9,52
|
31,43
|
|
1991
|
48
|
2
|
13
|
104,35
|
137,14
|
4,35
|
37,14
|
|
1992
|
48
|
0
|
13
|
100
|
137,14
|
0
|
37,14
|
|
1993
|
50
|
2
|
15
|
104,17
|
142,86
|
|
42,86
|
|
1994
|
50
|
0
|
15
|
100
|
142,86
|
0
|
42,86
|
|
1995
|
51
|
1
|
16
|
102,0
|
145,71
|
2,0
|
45,71
|
|
1996
|
52
|
1
|
17
|
101,96
|
148,57
|
1,96
|
48,57
|
Рассчитанные аналитические показатели характеризуют динамику ввода жилых
домов за 1987 – 1996 годы. Абсолютный прирост выражает абсолютную скорость
роста ввода жилых домов. По сравнению с 1987 годом она составила 17 тыс. м2.
Темп роста показывает, что ввод жилых домов 1996 г. составляет 148,57 %
от уровня базисного года. Темп прироста дает возможность оценить на сколько
процентов ввод жилых домов в 1996
г. возрос по сравнению с 1987 годом – на 48,57 %.
Рассчитаем средние показатели, тыс. м2:
а) средний абсолютный прирост:
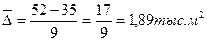
б) среднегодовой темп роста:
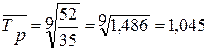
в) среднегодовой темп прироста:
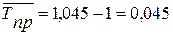
Среднегодовой ввод жилых домов составляет 45,9 тыс. м2. В
среднем в год ввод жилых домов увеличивался на 4,5 %.
3) Построим диаграмму данного ряда динамики.
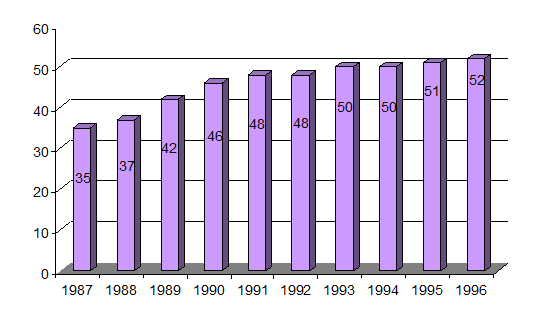
Рис.
1 Динамика ввода жилых домов за 1987 – 1996 годы.
Задание
4
По данным своего варианта (табл. 10) определите:
1) общие индексы:
а) цен;
б) физического объема проданных товаров;
в) товарооборота.
Какую роль в изменении товарооборота сыграли изменения цен и количества
проданных товаров?
2) Абсолютную величину изменения расходов населения, происшедших в связи
с изменением цен.
Таблица 10
Реализация
товаров в магазине
|
Номер варианта
|
Вид товара
|
Предыдущий период
|
Отчетный период
|
|
Кол-во, шт.
|
Цена за единицу, р.
|
Кол-во, шт.
|
Цена за единицу, р.
|
|
7
|
Соковыжималки
Фритюрницы
|
10
20
|
550
600
|
15
20
|
650
630
|
Решение
1) Общий индекс – это особая относительная величина, которая дает
количественную и качественную оценку изменения сложных экономических явлений во
времени, пространстве или по сравнению
с планом.
а) Общий индекс цен определяется по формуле:
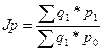 (18)
(18)
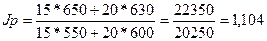
Это свидетельствует о том, что цены на оба товара в среднем выросли на
10,4 %.
б) Общий индекс физического объема товарооборота определяется по формуле:
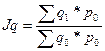 (19)
(19)
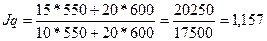
Это свидетельствует о том, что в отчетном периоде было продано больше
товаров на 15,7 %, чем в предыдущем периоде.
в) Общий индекс товарооборота определяется по формуле:
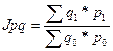 (20)
(20)
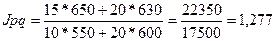
По сравнению с прошедшим периодом в отчетном периоде товарооборот
увеличился на 27,7%.
Прирост товарооборота за счет изменения цен составил:
∑р1q1 - ∑р0q1 =
22350-20250=2100 руб.
Прирост товарооборота за счет изменения количества проданных товаров составил:
∑р0q1 - ∑р0q0 =
20250-17500=2750 руб.
Общее изменение товарооборота составило:
∑р1q1 - ∑р0q0 =
22350-17500=4850 руб.
Можно сделать следующий вывод: в отчетном периоде по сравнению с
предыдущим товарооборот увеличился на 2100 руб. за счет увеличения цен на 10,4
% и на 2750 руб. за счет увеличения количества проданной продукции на 15,7%.
2) Абсолютная величина изменения расходов населения, происшедших в связи
с изменением цен составит:
∑(р1 – р0)*q1 = (650-550)*15+(630-600)*20 = 2100 руб.
В связи с повышением цен на товары расходы населения увеличились на 2100
рублей.
Задание 5
Для выявления зависимости между показателями рассчитайте линейный
коэффициент корреляции по исходным данным своего варианта, приведенным в табл.
1.
Корреляционная связь – это связь, проявляющаяся не в каждом случае, а в
массе случаев в средних величинах в форме тенденции.
Для определения степени тесноты парной линейной зависимости используют
линейный коэффициент корреляции (r).
По данным о стоимости нематериальных активов и величине балансовой
прибыли необходимо оценить тесноту связи.
Расчеты парного коэффициента корреляции следует произвести по следующей
формуле:
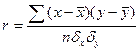 (21)
(21)
или
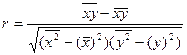 , (22)
, (22)
где х, у – индивидуальные значения факторного и результативного
признаков;
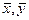 – средние значения признаков;
– средние значения признаков;
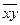 – средняя из
произведений индивидуальных значений признаков;
– средняя из
произведений индивидуальных значений признаков;
δх, δу
– средние квадратические отклонения признаков.
Расчеты указанных показателей произведем в табличной форме (табл. 11).
Таблица 11
Расчет
показателей парной корреляции
|
№ п/п
|
Стоимость
нематериальных активов, тыс.р. (х)
|
Балансовая прибыль,
тыс.р. (у)
|
ху
|
х2
|
у2
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
7
|
0
|
22,446
|
0
|
0
|
503,82
|
|
8
|
0
|
0,071
|
0
|
0
|
0,005
|
|
9
|
0,031
|
0,040
|
0,0012
|
0,001
|
0,0016
|
|
10
|
7,438
|
37,416
|
278,30
|
55,32
|
1399,96
|
|
11
|
0
|
4,100
|
0
|
0
|
16,81
|
|
12
|
6,375
|
1,116
|
7,11
|
40,64
|
1,24
|
|
13
|
1,067
|
0
|
0
|
1,14
|
0
|
|
14
|
0
|
4,957
|
0
|
0
|
24,57
|
|
15
|
10,631
|
9,838
|
104,59
|
113,02
|
96,79
|
|
16
|
0,406
|
0,632
|
0,26
|
0,16
|
0,40
|
|
17
|
3,100
|
14,453
|
44,80
|
9,61
|
208,9
|
|
18
|
2,419
|
50,890
|
123,10
|
5,85
|
2589,79
|
|
19
|
5,746
|
32,117
|
184,54
|
33,02
|
1031,50
|
|
20
|
7,428
|
24,541
|
182,29
|
55,17
|
602,26
|
|
21
|
5,846
|
3,244
|
18,96
|
34,17
|
10,52
|
|
22
|
19,665
|
2,870
|
56,44
|
386,71
|
8,24
|
|
23
|
7,752
|
11,309
|
87,67
|
60,09
|
127,89
|
|
24
|
15,755
|
38,654
|
608,99
|
248,22
|
1494,13
|
|
25
|
20,431
|
48,400
|
988,86
|
417,42
|
2342,56
|
|
26
|
10,356
|
19,120
|
198,01
|
107,25
|
365,57
|
|
27
|
9,300
|
15,545
|
144,57
|
86,49
|
241,65
|
Окончание
табл. 11
|
1
|
2
|
3
|
4
|
5
|
6
|
|
28
|
4,735
|
7,400
|
35,04
|
22,42
|
54,76
|
|
29
|
3,800
|
6,372
|
24,21
|
14,44
|
40,60
|
|
30
|
5,136
|
8,100
|
41,6
|
26,38
|
65,61
|
|
31
|
17,210
|
20,950
|
360,55
|
296,18
|
438,9
|
|
32
|
19,700
|
37,133
|
731,52
|
388,09
|
1378,86
|
|
33
|
20,600
|
31,500
|
648,9
|
424,36
|
992,25
|
|
34
|
17,840
|
36,100
|
644,02
|
318,26
|
1303,21
|
|
35
|
11,457
|
1,200
|
13,75
|
131,26
|
1,44
|
|
36
|
13,400
|
5,000
|
67,0
|
179,56
|
25,0
|
|
37
|
8,100
|
19,148
|
155,1
|
65,61
|
366,64
|
|
38
|
7,939
|
13,200
|
104,79
|
63,03
|
174,24
|
|
39
|
5,620
|
3,610
|
20,29
|
31,58
|
13,03
|
|
40
|
6,532
|
12,500
|
81,65
|
42,67
|
156,25
|
|
41
|
11,470
|
18,451
|
211,63
|
131,56
|
340,44
|
|
42
|
24,586
|
5,600
|
137,68
|
604,47
|
31,36
|
|
43
|
21,258
|
12,735
|
270,72
|
451,90
|
162,18
|
|
44
|
18,726
|
10,540
|
197,37
|
350,66
|
111,09
|
|
45
|
23,775
|
30,900
|
734,65
|
565,25
|
954,81
|
|
46
|
17,160
|
40,000
|
686,4
|
294,46
|
1600,0
|
|
47
|
4,170
|
6,541
|
27,28
|
17,39
|
42,78
|
|
48
|
3,560
|
8,900
|
31,68
|
12,67
|
79,21
|
|
49
|
6,500
|
2,156
|
14,01
|
42,25
|
4,65
|
|
50
|
25,120
|
45,820
|
1151,0
|
631,01
|
2099,47
|
|
51
|
1,500
|
0,550
|
0,825
|
2,25
|
0,3
|
|
52
|
3,750
|
3,450
|
129,37
|
14,06
|
11,9
|
|
53
|
3,600
|
6,114
|
22,01
|
12,96
|
37,38
|
|
54
|
5,020
|
2,777
|
13,94
|
25,2
|
7,71
|
|
55
|
0,186
|
0,130
|
0,024
|
0,034
|
0,017
|
|
56
|
4,807
|
1,445
|
6,95
|
23,11
|
2,09
|
|
50
|
Σ=451,273
|
Σ=740,081
|
Σ=9592,45
|
Σ=6836,81
|
Σ=21562,78
|
Рассчитаем величину линейного коэффициента корреляции:
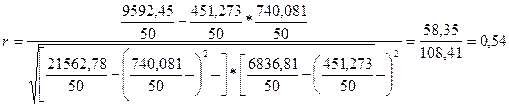
Коэффициент парной корреляции находится в пределах от 0,5 до 0,8, значит,
связь между признаками слабая.
СПИСОК
ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Едронова Н. Н. Общая теория статистики. – М.: Финансы и статистика, 2001.
– 648 с.
3. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика,
1998. – 368 с.
4. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. –
М.: ИНФРА-М. 2000. – 414 с.
5. Теория статистики / Под редакцией Громыко Г. Л. – М.: ИНФРА-М, 2002. – 576 с.
6. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и
статистика, 2002. – 576 с.