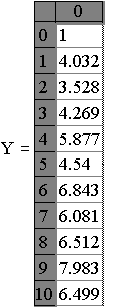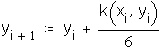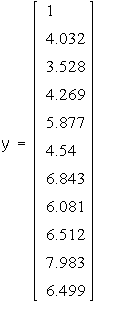Задача 189

Для функции, заданной таблично:

1) составить интерполяционный многочлен Лагранжа;

2) построить таблицу конечных разностей;

3) составить интерполяционный многочлен Ньютона для интерполяции вперед и назад;

4) вычислить приближенно (с 4 дес. зн.) значение функции в точке X^*;

X	4	5	6	7
Y	-3	-1	0	7

X^*=4.75

Решение.

1) Составим интерполяционный многочлен Лагранжа.

=

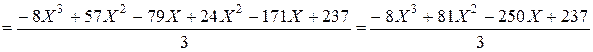
2) построим таблицу конечных разностей;

0,001048
0,001038	-0,000010
0,001038	-0,000008	0,000002
0,001030	-0,000008	0	-0,000002
0,001011	-0,000019	-0,000011	-0,000011
0,001002	-0,000009	0,000010	0,000021
0,000993	-0,000009	0	-0,000010
0,000984	-0,000009	0	0
0,000976	-0,000008	0,000001	0,000001
0,000966	-0,000010	-0,000002	-0,000003
-0,00009
0,000032	0,000041
-0,000031	-0,000063	-0,000104
0,000010	0,000041	0,000104	0,000208
0,000001	-0,000009	-0,000050	-0,000150
-0,000004	-0,000005	0,000004	0,000054
-0,000358
0,000204	0,000562

3) Многочлен Ньютона

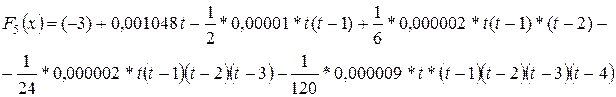
4) вычислим значение функции

Для значения х₁ = 4 будет t = 0,22.

В результате получается:

F₅ (х₁) = (-3) + 0,00023056 + 0,0000010296 + … = –2,888782.

Для значения х₂ = (-1)  будет t = 0,95

F₅ (х₂) = -1,898136.

Для значения х₃ = 0 будет

t = - 0,3;

F₅ (х₃) = 0,888227.

Для значения х₄ = 7 будет

t = 11;

F₅ (х₄) = 7,899585.

С точностью до 4 знака: F₅ (х₄) = 7,8996.

Задача 269

1)                      Решить задачу Коши Y’=F(X,Y),  Y(X0) на отрезке [0,1] методом Эйлера с шагом  Н=0.1.

2)                      Составить блок-схему и программу для решения задачи  методом Рунге-Кутта: Y’ = 0.2X + 0.04Y²,  Y(0)=1

Решение:

1) Явная схема Эйлера реализуется в MathCad следующим алгоритмом:

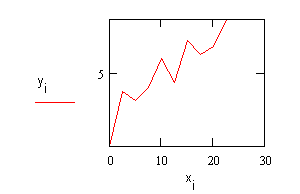
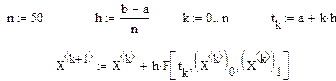Этот алгоритм в MathCad реализуется функцией

Ниже приведем программу в MathCad и результаты ее работы:

	правая часть дифференциального уравнения
	задание начальных условий
Х1:=1	конец отрезка интегрирования
	число точек разбиения отрезка интегрирования
	Решение дифференциальных уравнений в пакете MathCad осуществляется методом Эйлера.
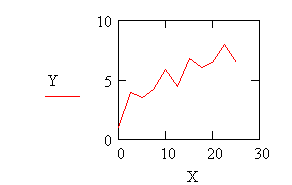
графическое решение уравнения и таблица значений функции у(х), полученные с помощью встроенных функций MathCad для решения дифференциальных уравнений

2) Приведем текст программы на MathCad и результаты ее работы

	правая часть дифференциального уравнения
	задание начальных условий
	число точек разбиения отрезка интегрирования
b:=1	границы отрезка интегрирования
	вычисление шага интегрирования
h = 0.1	значение шага интегрирования
расчетные формулы метода Рунге-Кутта, заданные в виде функций пользователя
построение точечного решения
графическое решение уравнения и таблица значений функции у(х)

Можно видеть, что результаты в пунктах 1 и 2 совпадают с точностью до 3 знака после запятой.