Содержание
Введение. 3
Портфельные риски. 6
САРМ – модель и бета-коэффициент. 9
Заключение. 17
Приложение 1. Бета-коэффициенты ликвидных Российских акций. 19
Задача №1. 24
Условие. 24
Решение. 25
Список
литературы.. 29
Введение
Избыточная наличность,
т.е. объём наличных средств фирмы, превышающая некоторый запланированный
уровень, необходимых для совершения сделок или поддержания компенсационных
остатков, инвестируются в рыночные ценные бумаги.
Решение об инвестировании
избытка наличности в рыночные ценные бумаги включает в себя не только
определение объёма инвестиций, но и типа ценной бумаги объекта
инвестиций. В какой-то степени эти 2 компонента решения взаимозависимы. Оба они
должны быть основаны на оценке ожидаемых чистых потоков наличности и доли
неопределённости, связанной с этими потоками. Если будущие потоки наличности
известны с достаточной степенью определенности, а кривая доходности возрастает,
т.е. долгосрочные ценные бумаги имеют более высокую доходность, чем
краткосрочные, то у компании может возникнуть стремление организовать свой
портфель таким образом, чтобы срок погашения ценных бумаг примерно
соответствовал тому моменту, когда понадобятся денежные средства. Модель потока
наличности предоставляет фирме большие возможности в плане максимизации средней
доходности всего портфеля, так как вероятность неожиданной продажи
значительного количества ценных бумаг невелика.
Ключевым фактором
является степень точности предсказаний потоков наличности. Если точность
высока, наиболее важной характеристикой становится срок погашения ценных бумаг.
Если будущие потоки наличности фирмы совершенно непредсказуемы, то самые важные
характеристики ценной бумаги это степень ее ликвидности и риск в отношении
колебаний её рыночной стоимости. Инвестируя средства в долгосрочные менее
ликвидные ценные бумаги с более высоким риском невыполнения обязательств, можно
однако, достичь более высокой доходности вложений. Кроме риска и недостатка
ликвидности, будут иметь место трансакционные издержки, сокращающие чистую
выручку. Таким образом фирма сталкивается с уже знакомой проблемой выбора между
риском и прибыльностью.
Чем больше объём портфеля
ценных бумаг, тем больше возможностей для специализации и экономии на затратах
труда по его обслуживанию
Занимаясь инвестициями,
необходимо выработать определенную политику своих действий и определить:
· основные цели инвестирования
(стратегический или портфельный его характер);
· состав инвестиционного портфеля,
приемлемые виды ценных бумаг;
· качество бумаги, диверсификацию
портфеля и т.д.
Под
инвестиционным портфелем понимается некая совокупность ценных бумаг. Обычно на
рынке продается некое инвестиционное качество с заданным соотношением
Риск/Доход, которое в процессе управления может быть улучшено[1].
Отцом современной теории
портфеля является Гарри Марковиц, получивший за свои труды в 1990 г.
Нобелевскую премию по экономике.
Суть теории Марковица состоит
в том, что, как правило, совокупный уровень риска может быть снижен за счет
объединения рисковых активов (это инвестиционные проекты и ценные бумаги) в
портфели. Основная причина такого снижения риска заключается в отсутствии
прямой функциональной связи между значениями доходности по большинству
различных видов активов.
Эта теория состоит из
следующих четырех разделов:
1. оценка
инвестиционных качеств отдельных видов финансовых инструментов инвестирования;
2. формирование инвестиционных решений
относительно включения в портфель индивидуальных финансовых инструментов
инвестирования;
3. оптимизация портфеля, направленная на
снижение уровня его риска при заданном уровне прибыльности;
4. совокупная оценка сформированного
инвестиционного портфеля по соотношению уровня прибыльности и риска.
Теория портфеля приводит к
следующим выводам:
1. для
минимизации риска инвесторам следует объединять рисковые активы в портфели;
2. уровень риска по каждому отдельному
виду активов следует измерять не изолированно от остальных активов, а с точки
зрения его влияния на общий уровень риска диверсифицированного портфеля
инвестиций.
Хотя теория портфеля в том
виде, в каком она была разработана Марковицем, учит инвесторов тому, как
следует измерять уровень риска, она не конкретизирует взаимосвязь между уровнем
риска и требуемой доходностью.
Данную взаимосвязь конкретизирует
модель оценки доходности финансовых активов (Capital Asset Pricing Model,
CAPM), разработанная более или менее независимо друг от друга Джоном Линтнером,
Яном Мойссином и Уильямом Шарпом.
Модель CAPM основана на
допущении наличия идеальных рынков капитала. Согласно этой модели, требуемая
доходность для любого вида рисковых активов представляет собой функцию трех
переменных:
Ø без
рисковой доходности,
Ø средней доходности на рынке ценных
бумаг,
Ø индекса колебания доходности данного
финансового актива по отношению к доходности на рынке в среднем.
Модель CAPM важна для
определения, как общей цены капитала фирмы, так и требуемой доходности для
отдельных проектов, осуществляемых в рамках фирмы.
Портфельные риски
Любое предприятие может
рассматриваться как совокупность некоторых активов (материальных и финансовых),
находящихся в определенном сочетании. Владение любым из этих активов связано с
определенным риском в плане воздействия этого актива на величину общего дохода
предприятия. То же самое в полном объеме относится к портфелям ценных бумаг,
причем, степень риска изменяется обратно пропорционально количеству включенных
в портфель случайным образом видов ценных бумаг (см. рис.1)[2].
Портфельный риск это
совокупный риск вложения капитала по инвестиционному портфелю в целом. В
результате диверсификации инвестиционного портфеля уровень портфельного риска
всегда ниже уровня риска отдельных входящих в него инструментов инвестирования
за счет эффекта диверсификации, уменьшающий несистематический риск.
Под диверсификацией понимают
расширение форм деятельности, видов продукции, используемых финансовых
инструментов с целью минимизации уровня хозяйственных рисков.
Диверсификация инвестиционного
портфеля это одна из видов инвестиционной политики предприятия в процессе
формирования портфеля ценных бумаг, направленных на снижение портфельного
несистематического риска (совокупный несистематический риск портфеля всегда
ниже суммы индивидуальных несистематических рисков отдельных фондовых
инструментов).
Общий риск портфеля
состоит из двух частей:
·
Диверсифицируемый
(несистематический) риск, т.е. риск, который может быть элиминирован за счет
диверсификации. Т.е. инвестирование 1 млн. рублей в акции десяти компаний менее
рискованно, чем инвестирование той же суммы в акции только одной компании.
Собственный риск - это часть общего риска, зависящая только от состояния дел в
данной компании, которое характеризуется неожиданными изменениями таких
факторов, как вероятность смены руководства, наличие
Рисунок 1 Зависимость степени риска от
диверсификации портфеля.
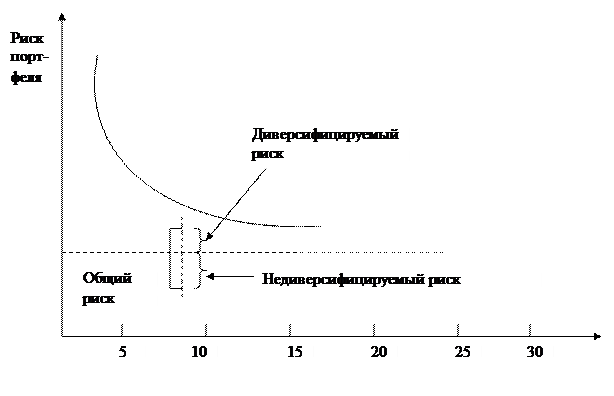
долгосрочных
договоров, просроченной дебиторской или кредиторской задолженности, показатели
финансового состояния и др.
·
Недиверсифицируемый
(систематический или рыночный) риск, т.е. риск, который нельзя снизить путем
изменения структуры портфеля. Систематический риск акции - это та часть общего
риска, которая зависит от факторов, общих для всего рынка ценных бумаг. К ним
относятся неожиданные изменения макроэкономических показателей (ВВП, скорость
промышленного роста, собираемость налогов, процентная ставка, уровень инфляции
и т. д.), изменение политической ситуации в стране или в мире, психологический
настрой участников рынка и др.
Как показали
исследования, если в портфель, с помощью случайной выборки из имеющихся на
рынке ценных бумаг включить 10-20 различных видов ценных бумаг, то риск может
быть сведен к минимуму (см. рис.1). Таким образом, этот риск поддается
элиминированию довольно простыми методами, поэтому основное внимание следует
уделять возможному уменьшению систематического риска.
Математически разделение
рисков можно провести на основе уравнения линейной регрессии, связывающего
доходность акции с доходностью по рыночному индексу. Коэффициент регрессии
называется коэффициентом бета ценной бумаги и является характеристикой ее
рыночного риска. В качестве рыночного обычно берется индекс, достаточно полно
отражающий состояние дел в экономике в целом и включающий курсы акций крупных
компаний в различных секторах рынка. В США для этих целей часто используют
индекс Standard&Poor's 500. Для российского рынка в качестве такого индекса
можно рекомендовать сводный индекс АК&М, МТ-индекс или любой другой,
включающий достаточно представительную выборку акций из разных отраслей. Обычно
за основу расчета индекса берется капитализация входящих в него ценных бумаг.
Рассмотренное
представление общего риска ценной бумаги в виде суммы собственного и
несобственного рисков является далеко не единственным. Часто общий риск
представляют в виде суммы трех слагаемых, где в качестве третьей компоненты
выступает риск отрасли, к которой относится компания. Наконец, можно
использовать и многофакторные модели.
САРМ – модель и бета-коэффициент
Как уже отмечалось выше,
существует, так называемая, теория портфеля – теория финансовых инвестиций, в
рамках которой с помощью статистических методов и осуществляются наиболее
выгодное распределение риска портфеля ценных бумаг и оценка прибыли. Эта теория
состоит из четырех основных элементов:
·
оценка
активов;
·
инвестиционные
решения;
·
оптимизация
портфеля;
·
оценка
результатов.
В процессе управления
инвестиционным портфелем менеджер постоянно сталкивается с задачей отбора новых
инструментов и анализа возможности их включения в портфель. Это можно делать с
помощью нескольких методов, однако наибольшую известность получила модель
оценки доходности финансовых активов (Capital Asset Pricing Model, CAPM), увязывающая систематический риск и
доходность портфеля (см. рис.2).
Рисунок 2 Логика представления модели
САРМ
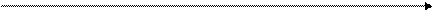






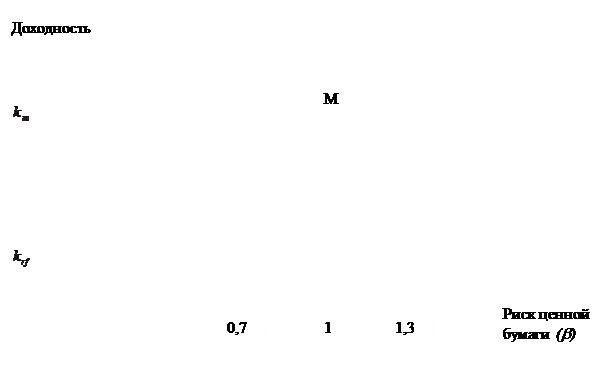
К основным предпосылкам модели CAPM можно отнести следующие:
·
Основной
целью каждого инвестора является максимизация возможного прироста своего
богатства на конец планируемого периода путем оценки ожидаемых доходностей и
среднеквадратических отклонений альтернативных инвестиционных портфелей.
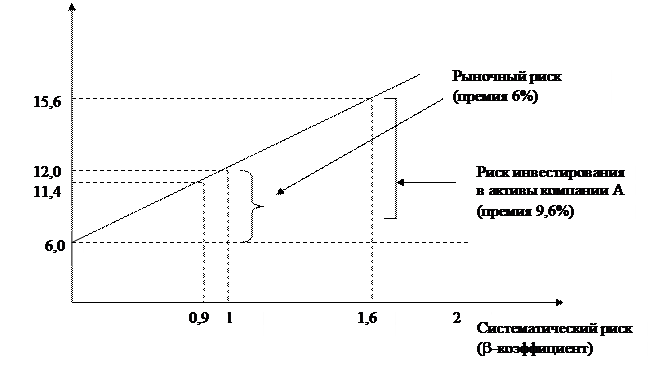
·
Все
инвесторы могут брать и давать ссуды неограниченного размера по некоторой
безрисковой процентной ставке 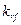 , при этом не существует ограничений на «короткие[3]»
продажи любых активов.
, при этом не существует ограничений на «короткие[3]»
продажи любых активов.
·
Все
инвесторы одинаково оценивают величину ожидаемых значений доходности, дисперсии
и ковариации всех активов; это означает, что инвесторы находятся в равных
условиях в отношении прогнозирования показателей.
·
Все
активы абсолютно делимы и совершенно ликвидны.
·
Не
существует трансакционных расходов.
·
Не
принимаются во внимание налоги.
·
Все
инвесторы принимают цену как экзогенно заданную величину (т.е. не принимается
во внимание, то, что действия инвесторов по покупке и продаже ценных бумаг
могут оказывать влияние на уровень цен на рынке этих бумаг).
·
Количество
всех финансовых активов заранее определено и фиксировано.
Для инвестиционного
портфеля коэффициент бета вычисляется путем сложения коэффициентов бета входящих
в него бумаг, умноженных на соответствующие веса (вес каждой бумаги в портфеле
равен частному от деления ее совокупной стоимости в портфеле к стоимости всего
портфеля). Наиболее интересный вывод с точки зрения портфельного менеджмента
заключается в том, что хорошо диверсифицированный портфель не имеет
собственного риска, т. е. изменение его доходности равно изменению доходности
рыночного индекса, умноженного на коэффициент бета портфеля. Это означает, что
поведение хорошо диверсифицированного портфеля ничем (с точностью до умножения
на константу) не отличается от поведения рыночного индекса.
Главная задача, которую
поставил и полностью решил Марковиц, формулировалась так: инвестор хочет
получить доходность, равную r, исходя из некоторого набора ценных бумаг. Каким
образом он должен составить портфель с наименьшим общим риском, имеющий среднюю
доходность r? Это - типичная оптимизационная задача. Полученный портфель
определяется однозначно как показателями средней доходности и риска бумаг из
набора, так и ковариациями между ними, и называется эффективным портфелем. При
этом, естественно, большему значению r будет соответствовать и большее значение
общего риска портфеля.
Взаимосвязь между
ожидаемой доходностью (y) и риском
ценной бумаги (x) находится путем построения функции 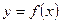 . Построение основывается на следующих рассуждениях:
. Построение основывается на следующих рассуждениях:
·
доходность
ценной бумаги связана с присущим ей риском прямой связью;
·
риск
характеризуется показателем b;
·
«средней»
ценной бумаге, т.е. бумаге, имеющей средние значения риска и доходности,
соответствует  и доходность
и доходность 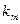 ;
;
·
имеются
безрисковые ценные бумаги со ставкой 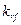 и
и 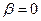 .
.
Исходя из перечисленных предпосылок, доказывается,
что искомая зависимость 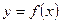 представляет собой
прямую линию. Подставив в уравнение прямой исходные данные, получим следующую
формулу:
представляет собой
прямую линию. Подставив в уравнение прямой исходные данные, получим следующую
формулу:
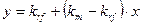
Учитывая, что переменная x представляет собой риск, характеризуемый показателем b, а y - ожидаемую доходность 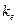 , получим формулу, представляющую собой модель САРМ:
, получим формулу, представляющую собой модель САРМ:
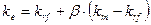 ,
,
где 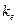 - ожидаемая доходность
акций данной компании;
- ожидаемая доходность
акций данной компании;
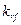 - доходность безрисковых ценных бумаг;
- доходность безрисковых ценных бумаг;
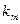 - ожидаемая доходность в среднем на рынке ценных бумаг;
- ожидаемая доходность в среднем на рынке ценных бумаг;
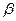 - бета – коэффициент
данной компании
- бета – коэффициент
данной компании
Показатель 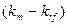 имеет вполне наглядную интерпретацию, представляя собой
рыночную премию за риск вложения своего капитала не в безрисковые
государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации
корпораций и пр.). Аналогично показатель
имеет вполне наглядную интерпретацию, представляя собой
рыночную премию за риск вложения своего капитала не в безрисковые
государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации
корпораций и пр.). Аналогично показатель 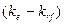 представляет собой премию за риск вложения капитала в ценные
бумаги именно данной компании. Модель САРМ означает, что премия за риск
вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии
за риск.
представляет собой премию за риск вложения капитала в ценные
бумаги именно данной компании. Модель САРМ означает, что премия за риск
вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии
за риск.
Модель САРМ позволяет
спрогнозировать доходность финансового актива; в свою очередь, зная этот показатель
и имея данные об ожидаемых доходах по этому активу, можно рассчитать его
теоретическую стоимость. Именно поэтому модель САРМ называют еще моделью
ценообразования финансовых активов.
Систематический риск в рамках
модели САРМ измеряется с помощью b - коэффициента
(бета-коэффициента).
b - коэффициент (англ. beta
coefficient) - величина риска по отношению к определенной ценной бумаге. Т.е. b
- коэффициент – это единица измерения, которая дает количественное соотношение
между движением курса данной акции и движением рынка акций в целом.
Каждый вид ценной бумаги имеет
свой собственный бета-коэффициент. Значение показателя b
рассчитывается по статистическим данным для каждой компании, котирующей свои
ценные бумаги на бирже, и периодически публикуются в специальных справочниках.
Для каждой компании b меняется с течением времени и
зависит от многих факторов, в частности имеющих отношение к характеристике
деятельности компании с позиции долгосрочной перспективы. Сюда относятся,
прежде всего, показатель уровня финансового левериджа, отражающего структуру
источников средств: при прочих равных условиях, чем выше доля заемного
капитала, тем более рисковая компания и тем выше ее b[4].
Также значение b
зависит и от уровня операционного левериджа, т.е. чем больше доля постоянных
расходов в общей их сумме, тем выше b.
Общая формула расчета
бета-коэффициента для произвольной
компании имеет вид:
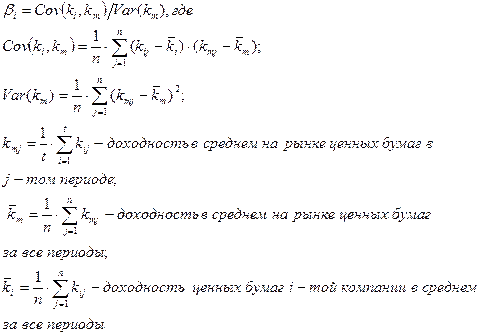
В целом по рынку ценных бумаг бета-коэффициент
равен единице; для отдельных компаний он колеблется около единицы, причем
большинство бета-коэффициентов находится в интервале от 0,5 до 2,0.
Интерпретация бета-коэффициентов для акций конкретной компании заключается в
следующем:
·
Бета>1, - акция считается
рисковой
·
Бета=1, - акция равна рынку
·
Бета<1, - акция считается
защитной
·
Бета=0, - акция считается
безрисковой.
Увеличение бета-коэффициента в
динамике означает, что вложения в ценные бумаги данной компании становится
более рискованным, а снижение бета-коэффициента в динамике означает
соответственно, что вложения в ценные бумаги данной компании становится менее
рискованными.
Важно отметить, что единого
подхода к исчислению b-коэффициентов, в частности в
отношении количества и вида исходных наблюдений не существует. Так, например
одна компания при расчете b-коэффициентов в качестве 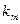 может использовать индекс курсов акций одной биржи и месячные
данные о доходности компаний за пять лет, а другая компания может
ориентироваться на индекс курсов акций другой биржи и использовать большее количество
наблюдений.
может использовать индекс курсов акций одной биржи и месячные
данные о доходности компаний за пять лет, а другая компания может
ориентироваться на индекс курсов акций другой биржи и использовать большее количество
наблюдений.
На российском рынке ценных
бумаг понятие b-коэффициента
появилось в 1995году. Но в список наблюдений попадает ограниченное количество
компаний, как правило, это предприятия энергетики и нефтегазового комплекса[5]. При
этом значения b-коэффициентов
достаточно ощутимо варьируются.
Линейная зависимость «доходность/риск» для конкретных ценных бумаг может быть представлена с помощью
графика, носящего название линии рынка ценных бумаг (Security Market
Line, SML – рис.3.)
Рисунок 3 график линии рынка ценных бумаг
|
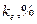 15,6 15,6
|
|
Важным свойством модели САРМ
является ее линейность относительно степени риска. Это дает возможность, как
отмечалось выше, определять бета-коэффициент портфеля как средневзвешенную b-коэффициентов
входящих в портфель финансовых активов:
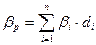 ,
,
где 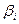 - значение бета-коэффициента i-го актива в портфеле;
- значение бета-коэффициента i-го актива в портфеле;
 - значение бета-коэффициента портфеля;
- значение бета-коэффициента портфеля;
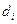 - доля i-го актива в портфеле;
- доля i-го актива в портфеле;
n- число
различных финансовых активов в портфеле.
Обобщением понятия «линия
рынка ценных бумаг» является линия рынка капитала (Capital Market
Line, CML),
отражающая зависимость (доходность/риск) для эффективных портфелей, которые,
как правило, сочетают безрисковые и рисковые активы.
Линию рынка капитала можно
использовать для сравнительного анализа портфельных инвестиций. Как следует из
модели САРМ, каждому портфелю соответствует точка в квадранте (см. рис.3). Возможны
три варианта расположения этой точки:
1. на
линии рынка капитала (в этом случае портфель называется эффективным);
2. ниже
линии рынка капитала (неэффективный портфель);
3. выше
линии рынка капитала (сверхэффективный портфель).
Заключение
Модель САРМ разработана из
ряда предпосылок, часть из которых не выполняются на практике. Так например,
налоги и трансакционные затраты существуют, инвесторы находятся в неравных
условиях и т.д. Поэтому модель не может являться идеальной и зачастую
подвергается критике. Существуют различные точки зрения по поводу модели, к
наиболее типовым о ней представлениям относят следующие:
1. Концепция
САРМ, в основе которой лежит приоритет рыночного риска перед общим, является
весьма полезной, имеющей фундаментальное значение в концептуальном плане.
Модель логично отражает поведение инвестора, стремящегося максимизировать свой
доход при заданном уровне риска и доступности данных[6].
2. Теоретически
САРМ дает однозначное и хорошо интерпретируемое представление о взаимосвязи между
риском и требуемой доходностью, однако она предполагает, что для построения
связи должны использоваться априорные ожидаемые значения переменных, в то время
как в распоряжении аналитика имеются лишь апостериорные фактические значения.
Поэтому оценки доходности, найденные с помощью модели, потенциально содержат
ошибки.
3. Некоторые
исследования, посвященные эмпирической проверки модели, показали на
значительные отклонения между фактическими и расчетными данными, что позволяет
ряду ученых подвергать эту теорию серьезной критике. Их оппоненты же считают,
что модель САРМ описывает взаимосвязи между ожидаемыми значениями переменных,
поэтому любые выводы, основанные на эмпирической проверке статистических
данных, не правомочны и не могут опровергать теорию[7].
В целом многие ученые понимают,
что к одному из основных недостатков модели относится то, что она является
однофакторной. В научной литературе известны три основных подхода,
альтернативные модели САРМ:
1. теория
арбитражного ценообразования;
2. теория
ценообразования опционов и
3. теория
преференций состояний в условиях неопределенности.
Приложение 1.
Бета-коэффициенты ликвидных Российских акций
Первоначально бета-коэффициент
рассчитывался по индексу РТС. Однако в связи с новой методикой его подсчета
(большой вес в индексе акции ЛУКОЙЛа), а также различием во времени закрытия
РТС с ММВБ данный подход теряет свою актуальность. И расчет бета-коэффициентов
со второго квартала 2004 производится уже по индексу ММВБ.
В приложении рассматриваются
некоторые итоги третьего 2004 года. При этом очерк разбит на 2 части.
В июле 2004 года
утверждался тезис о том, что средняя цена сделок (за полугодие) по
защитной акции должна выступать или поддержкой или ориентиром для роста в
третьем квартале. И наоборот, средняя цена сделок (за полугодие) по рисковым
акциям должна выступать как сопротивление или ориентир для падения в третьем
квартале. Таким образом, была сформулирована Теорема о средней.
Если акция является
рисковой по критерию бета в отчетном периоде, то и средняя цена сделок за
этот отчетный период является рисковой ценой в данном текущем периоде.
С другой стороны, если
акция является защитной, то средняя цена сделок в отчетном периоде может
выступать как ориентир для покупок в текущем периоде[8].
Таблица 1
|
Название
|
Бета-коэффициент
За 2 квартала 2004
|
Средняя цена за
2 квартала 2004
|
Бета-коэффициент
За 3 квартала 2004
|
Средняя цена за
3 квартала 2004
|
|
Лукойл
|
0,997
|
804,5
|
0,967
|
810,96
|
|
Юкос
|
1,646
|
325,51
|
2,174
|
249,1
|
|
Норильский никель
|
1 ,257
|
1961,7
|
1,278
|
1833,1
|
|
Ростелеком
|
0,834
|
65,95
|
0,966
|
63,93
|
|
Сбербанк
|
0,788
|
11093,8
|
0,73
|
11074,3
|
|
Газпром
|
0,8
|
50,48
|
0,8
|
57,05
|
|
РАО ЕЭС
|
1,07
|
8,63
|
1,077
|
8,27
|
|
Сургутнефтегаз
|
1,013
|
18,96
|
0,975
|
19,14
|
|
Мосэнерго
|
0,601
|
2,353
|
0,65
|
2,49
|
|
Уралсвязьинформ
|
0,692
|
1,1658
|
0,541
|
1,0986
|
|
Автоваз
|
0,54
|
841,7
|
0,558
|
813
|
|
Сибнефть
|
0,833
|
92,82
|
0,868
|
90,86
|
|
Татнефть
|
0,806
|
37,6
|
0,755
|
37,74
|
|
Иркутскэнерго
|
0,75
|
5,78
|
0,81
|
5,53
|
1) Акция Лукойла.
Ее бета-коэффициент в первом полугодии составил 0,997(акция практически равна
рынку) при средней цене сделок 804,5.
Минимум третьего
квартала составил 701 рубль, максимум 942 рубля. По итогам же трех
кварталов 2004г. бета составил 0,967 (защитная акция), а средняя цена сделок
(здесь и далее за три квартала) 810,96.
2) Акция Юкоса.
Бета- коэффициент акции в первом полугодии составил 1,646 (т.е. акция
сверхрискованная) при средней цене сделок 325,51.
Максимум третьего
квартала составил 276 рубль, минимум 79 рублей. По итогам же трех кварталов
бета составил 2,174 (т.е. акция сверхрискованная), а средняя цена сделок 249,1.
3) Акция
Норильского никеля. Бета-коэффициент акции в первом полугодии составил 1,257
(т.е. акция достаточно рискованная) при средней цене сделок
1961,7
Минимум третьего квартала
составил 1292 рубль, максимум 1885 рублей (30 сентября). По итогам же трех
кварталов бета составил 1,278 (т.е. акция достаточно рискованная ), а средняя
цена сделок 1833,1.
4) Акция Ростелекома. Ее
бета в первом полугодии составил 0,834(акция строго защитная) при средней цене
сделок 65,95.
Минимум третьего
квартала составил 51,13 рубль, но дальше к концу квартала акция росла, и
максимум 30 сентября составил 65,84 рубля. По итогам же трех кварталов
2004г. бета составил 0,966 (защитная акция), а средняя цена сделок 63,93.
5) Акция Сбербанка. Ее
бета в первом полугодии составил 0,788 (акция строго защитная) при средней цене
сделок 11093,8.
Минимум третьего
квартала составил 10310 рубля, максимум 12856 . По итогам же трех
кварталов 2004г. бета составил 0,73 (строго защитная акция), а средняя цена
сделок 11074,3.
6) Акция Газпрома. Ее
бета в первом полугодии составил 0,8 (акция строго защитная) при средней цене
сделок 50,48.
Минимум третьего
квартала составил 49,5 рубля (1 июня), максимум 76,33 . По итогам же
трех кварталов 2004г. бета составил снова 0,8 (строго защитная акция), а
средняя цена сделок уже 57,05.
7) Акция РАО ЕЭС. Бета-
коэффициент акции в первом полугодии составил 1,07 (т.е.
акция рискованная) при средней цене сделок 8,63
Минимум третьего квартала
составил 6,57 рубля, максимум 8,54 рублей (30 сентября). По итогам же трех
кварталов бета составил 1,077 (т.е. акция рискованная ), а средняя цена
сделок 8,27.
8) Акция Сургутнефтегаз.
Ее бета в первом полугодии составил 1,013 (акция слегка с риском, но равна в
принципе рынку) при средней цене сделок 18,96.
Минимум третьего
квартала составил 17,20 рубля, максимум 21,94 рубля. По итогам же трех
кварталов 2004г. бета составил 0,975 (защитная акция), а средняя цена сделок
(здесь, как и выше и далее за три квартала) 19,14.
9) Акция Мосэнерго. Ее
бета в первом полугодии составила 0,601 (акция сверх защитная), при средней
цене сделок 2,353.
Минимум третьего
квартала составил 1,939 рубля , максимум 4,439 . По итогам же трех
кварталов 2004г. бета составил снова 0,65 (сверх защитная акция), а средняя
цена сделок только 2,49.
10) Акция
Уралсвязьинформа. Ее бета в первом полугодии составил 0,692 (акция строго
защитная) при средней цене сделок 1,1658.
Минимум третьего
квартала составил 0,82 рубля , максимум 15 июня 1,19. Закрытие 30 сентября
1,095 . По итогам же трех кварталов 2004г. бета составил снова 0,541
(сверх защитная акция), а средняя цена сделок уже 1,0986.
11) Акция Автоваза. Ее
бета в первом полугодии составила 0,54 (акция сверх защитная) при средней цене
сделок 841,7.
Минимум третьего
квартала составил 601 рубль, максимум 28 сентября 774. По итогам же трех
кварталов 2004г. бета составил снова 0,558 (сверх защитная акция), а средняя
цена сделок уже 813.
12) Акция Сибнефти. Ее
бета в первом полугодии составил 0,833 (акция строго защитная) при средней цене
сделок 92,82.
Минимум третьего
квартала составил 67 рубля , максимум 30 сентября 102. По итогам же трех
кварталов 2004г. бета составил снова 0,868 (строго защитная акция), а средняя
цена сделок уже 90,86.
13) Акция Татнефти. Ее
бета в первом полугодии составил 0,806 (акция строго защитная) при средней цене
сделок 37,6.
Минимум третьего
квартала составил 29,95 рубля, максимум 21 сентября 47,1. По итогам же
трех кварталов 2004г. бета составил снова 0,755 (строго защитная акция), а
средняя цена сделок уже 37,74.
14) Акция Иркутскэнерго.
Ее бета в первом полугодии составил 0,75 (акция строго защитная) при средней
цене сделок 5,78.
Минимум третьего
квартала составил 3,65 рубля, максимум 6,039. По итогам же трех
кварталов 2004г. бета составил снова 0,81 (строго защитная акция), а средняя
цена сделок уже 5,53[9].
Задача №1
Условие
По данным таблицы №1 (X –
готовая продукция на складе предприятия; Y – выручка от реализации продукции)
найти параметры уравнения регрессии методом наименьших квадратов. Для проверки
адекватности уравнения регресии определить величину среднего относительного
отклонения.
По полученному уравнению
регрессии для среднегодовой величины готовой продукции на складе предприятия
(определяется как среднеарифметическое значение X) найти выручку от реализации
продукции на следующий год.
Составить бюджет движения
денежных средств. Определить критический период в деятельности предприятия и
сделать выводы. Исходные данные для составления бюджета: объемы продаж
увеличиваются с темпом прироста 1,5% в месяц от базового месяца (декабрь
текущего года). Предприятие проводит индивидульную сбытовую политику на основе
применения различных видов реализации при разных условиях оплаты: 25% изделий
реализуется за наличный расчет. 75% с отсрочкой платежа на условиях 3/10 брутто
30: 80% оплачивается в следующем месяце, из них 25% со скидкой, а 20%
оплачиваются с задержкой еще на один месяц.
Сырье закупается в
размере потребности следующего месяца, оплата поставщикам производится через
месяц. Прогнозируемое увеличение цен на сырье 3% в месяц.
Издержки определяются в %
от выручки базового месяца, из них условно-переменные: сырье – 40;
условно-постоянные: заработная плата – 15; аренда производственных площадей –
10; прочие расходы – 5. Уровень инфляции в месяц 2%. Аренда и заработная плата
выплачивается в месяц, следующий за месяцем их возникновения. Единый социальный
налог (ЕСН) составляет 35,6% от заработной платы. Ставка налога на прибыль 24%
В конце каждого квартала планируется
вкладывать в модернизацию производства 1 млн рублей. Остаток средств на 1
января составляет 500 тысяц рублей. Этой суммы недостаточно и решено иметь
целевой остаток 600 тысяч рублей. Его величина в последующие месяцы изменяется
пропорционально темпу инфляции
Решение
Таблица 1
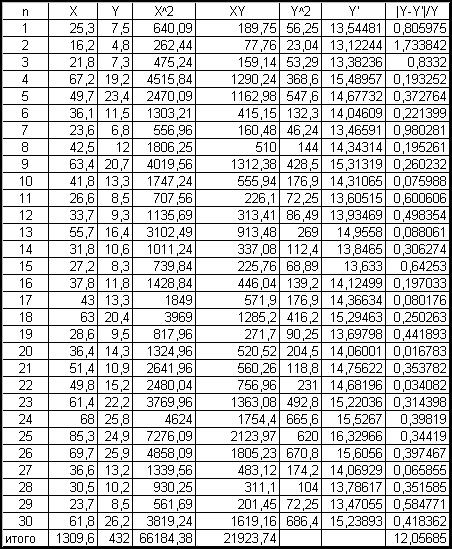
Найдем коэффициенты
регрессии
Сформулируем систему
уравнений для поиска коэффициентов регрессионной модели по МНК
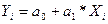 - функция
регрессионной модели
- функция
регрессионной модели
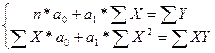
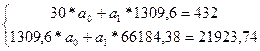
Из данного уравнения
отсюда 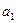 = 0,0464;
= 0,0464; 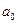 = 12,371
= 12,371
или 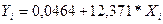
Определим величину
среднего относительного отклонения
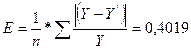 > 15%, что
свидетельствует о недостаточно тесной связи факторного и результатирующего
признака.
> 15%, что
свидетельствует о недостаточно тесной связи факторного и результатирующего
признака.
Определим величину
среднемесячной выручки на следующий год
Определим среднее
количество остатков готовой продукции за период (как среднеарифметическое)
Xср = 43,653
Таким образом, величина
выручки (в месяц) составит (в среднем по году)
Y расч = 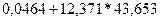 = 14,397
= 14,397
Составим расчет
движения денежных средств на год (БДДС на год)
Примечание – в качестве
базового периода для определения выручки принимается декабрь текущего года (не
расчетная средняя выручка), так как в условии задачи определен темп роста
выручки именно от этого показателя

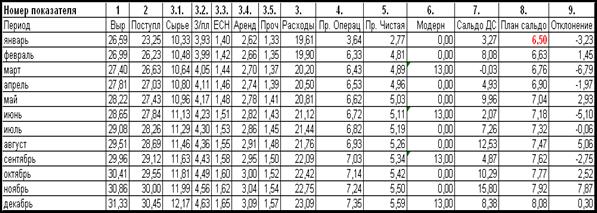
Описание показателей:
1.
Выручка
от реализации (с учетом темпа роста 1,5% в месяц)
2.
Поступление
денежных средств (с учетом вида расчетов см. таблицу №3)
3.
Расход
денежных средств
3.1.
Сырье
(40% суммы выручки следующего периода, минус величина товарного кредита 3%;
расходы следующего месяца)
3.2.
Заработная
плата (% от выручки; расходы следующего месяца)
3.3.
ЕСН
(% от з/пл; расходы следующего месяца)
3.4.
Аренда
(% от выручки; расходы следующего месяца)
3.5.
Прочие
расходы (% от выручки; расходы текущего месяца)
4.
Валовая
прибыль (2)-(3)
5.
Чистая
прибыль (после уплаты налога на прибыль) (за вычетом налога на прибыль)
6.
По
инвестиционной деятельности (1 млн рублей в квартал)
7.
Сальдо
денежных средств на конец месяца (накопленный остаток плюс чистая прибыль)
8.
Плановое
сальдо остатков денежных средств (с учетом инфляции 2% в месяц)
9.
Отклонение
планового сальдо от фактического (разница планового и фатического сальдо)
Таблица №3 «Поступление
от продаж текущего периода»
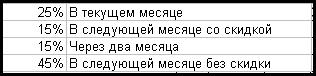
Выводы
Как свидетельствуют
приведенные расчеты, предприятие в планируемом году, на протяжении всего года
имеет положительное сальдо по счетам денежных средств В результате
планирования, предприятию удалось сформировать план расходов таким образом, что
плановое сальдо на протяжении всего года либо было либо незначительно выше
фактического, либо ниже его, кроме марта, июня и сентября, когда производились
вложения в модернизацию.
На конец периода
предприятие выходит на уровень сальдо денежных средств равного планируемуму
Список литературы
1. Бригхем Ю. Финансовый менеджмент.
- Спб.: Экономическая школа, - 1997. –
669с.
2. Ван Хорн Дж. Основы управления
финансами. – М.: Финансы и статистика. 1996, - 800с.
3. Бланк И.А. Основы финансового
менеджмента. – Киев: Ника-Центр, 2001, - Т.1. – 592с.
4. Ковалев В.В. Введение в финансовый
менеджмент. – М.: Финансы и статистика, 2002. – 768с.
5. Ковалев В.В. Финансовый анализ:
Управление капиталом. Выбор инвестиций. Анализ отчетности. – М.: Финансы и статистика,
1997. – 512с.
6. Миркин Я.М. Ценные бумаги и фондовый
рынок. – М.: «Перспектива», 1995,- 532с.
7. Семенкова Е.В. “Операции с ценными
бумагами”, М., Перспектива, Инфра-М, 1997, - с. 237
8. Рынок ценных бумаг. Учебник/Под ред.
В.А. Галанова. – М.: Финансы и статистика, 1996.
9. Интернет-ресурсы: www.cfin.ru
10.
Интернет-ресурсы:
www.gaap.ru
[1] Семенкова Е.В. “Операции с ценными
бумагами”, М., Перспектива, Инфра-М, 1997, - с. 237
[2] Ковалев В.В. Введение в
финансовый менеджмент. – М.: Финансы и статистика, 2002. – с. 424-425
[3] «Короткая продажа» -
продажа ценных бумаг, которыми инвестор не владеет. Инвестор продает ценные
бумаги в надежде на то, что в ближайшее время цена этих активов будет падать и
можно будет прикупить недостающие бумаги.
[4] Ковалев В.В. Введение в
финансовый менеджмент. – М.: Финансы и статистика, 2002. – с. 427
[5] См. приложение 1.
[6] Бригхем Ю. Финансовый
менеджмент. - Спб.: Экономическая школа,
- 1997. – 669с.
[7] Там же
[8] в качестве средней цены
используется взвешенная цена сделок по итогам дня (а не цена закрытия).
[9] Данные web-сайта www.cfin.ru