Задача
1
Предложить оптимальное управленческое решение
в следующих типовых
хозяйственных ситуациях.
Распределение рекламного бюджета.
1.7.Фирма рекламирует свою продукцию с
использованием четырех средств: телевидения, радио, газет и афиш. Из различных
рекламных экспериментов, которые
проводились в прошлом, известно, что эти средства приводят к увеличению прибыли
соответственно на 10, 3, 7 и 4 у.е. в расчете на 1 у.е., затраченную на
рекламу.
Распределение рекламного бюджета по различным
средствам подчинено следующим ограничениям:
а) полный бюджет не должен превосходить 500 000 у.е.;
б) следует расходовать не более 40 % бюджета на
телевидение и не более 20 %
бюджета на афиши;
в) вследствие привлекательности для подростков радио
на него следует
расходовать по крайней мере половину
того, что планируется на телевидение.
Сформулируйте задачу распределения средств по различным источникам как
задачу линейного программирования и
решите ее.
Решение.
Экономико-математическая модель задачи.
Переменные: х1 -
расходы на рекламу на телевидении, х2- на радио, х3-
в газетах,
х4- на афишах.
Целевая функция: f(X) = 10 Xi + 3 х2 + 7 х3 + 4 х4 -> max
Условие неотрицательности переменных: xj > 0 (j = 1.. .4)
Система ограничений:
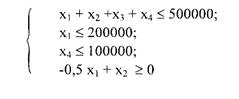
Решение с помощью надстройки «Поиск решения».
Задачу будем решать с помощи надстройки «Поиск
решения» Microsoft Excel.
Вначале подготовим электронную таблицу (лист)
Excel для применения
данной
надстройки, покажем ввод необходимых
параметров, а затем найдем
оптимальное решение.
Введем значения коэффициентов целевой функции:

|
Запишем систему
ограничений на значения переменных:
|
Введем на лист Excel ячейки, в которых будет помещен результат
решения (оптимальный план расходов на рекламу), и
присвоим ячейкам первоначальные значения переменных.

 Установим расположение ячейки, в которой
будет вычисляться значение целевой
функции:
Установим расположение ячейки, в которой
будет вычисляться значение целевой
функции:
В ячейку для вычисления целевой функции
введем формулу для вычисления целевой
функции:

Задание формулы для вычисления целевой
функции (суммы произведений элементов
векторов: плана расходов и коэффициентов целевой функции):

Откроем диалоговое окно «Поиск решения». В нем
зададим расположение целевой ячейки (в котором вычисляется значение целевой
функции), вид оптимального
решения (максимальное значение), расположение ячеек, которые
будут изменяться при поиске решения (из них
состоит вектор-строка оптимального плана), а также ограничения на изменяемые
значения.

После ввода необходимых данных нажмем кнопку
«Выполнить» диалогового окна. В случае, если решение существует (и все данные
введены верно), появляется сообщение:

После нажатия кнопки «ОК» в ячейках строки
оптимального плана появляются значения
его оптимальных элементов (оптимальный план); в ячейке целевой функции
вычисляется соответствующее этому плану оптимальное значение целевой функции.
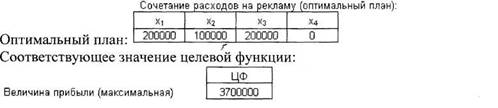
Выводы.
Оптимальный план: (200000; 100000; 200000; 0).
Максимальное значение прибыли от рекламы: 3 700 000 у.е. Как видно из
оптимального плана, на рекламу с помощью афиш расходовать средства нерационально. Это связано с
относительно небольшим увеличением прибыли от этого вида рекламы и отсутствия привлекательности для
какой-либо категории населения (в отличие, например, от радио).
Задача 2
Провести моделирование и решить специальную
задачу линейного
программирования.
Задача о назначениях.
Задача 2.7.
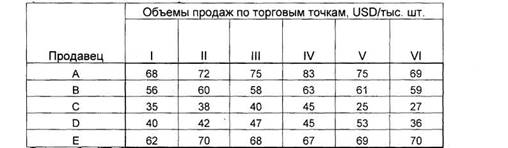
В распоряжении некоторой компании имеется 6
торговых точек и 5 продавцов. Из
прошлого опыта известно, что эффективность работы продавцов в различных
торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца
в каждой торговой точке. Результаты этой оценки представлены в таблице.
 Как коммерческий директор должен осуществить
назначение продавцов по торговым
точкам, чтобы достичь максимального объема продаж?
Как коммерческий директор должен осуществить
назначение продавцов по торговым
точкам, чтобы достичь максимального объема продаж?
2.1 .Матрица назначений.
Решение.
Экономико-математическая модель задачи.
Переменные:
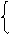
 ..
0, если продавец i не
назначен на торговую точку j;
..
0, если продавец i не
назначен на торговую точку j;
XI]
=
1, если продавец i назначен на торговую точку j Целевая функция - объем продаж на всех торговых точках, необходимо
достичь максимального объема продаж:
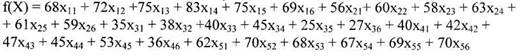
Функциональные ограничения. По
работникам (по бригадам):
Задачу будем решать с помощи, надстройки
«Поиск решения» Microsoft Excel. Вначале подготовим электронную таблицу (лист) Excel для применения данной надстройки, покажем ввод необходимых
параметров, а затем найдем оптимальное решение. Подробно разберем применение
надстройки при решении задачи.
Введем на лист Excel исходные данные (матрицу объемов продаж по
торговым точкам).
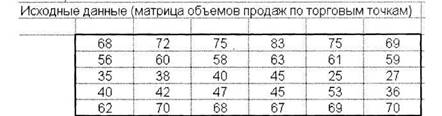
 Введем первоначальные значения матрицы
изменяемых ячеек (матрицы ' назначений). Затем в эти ячейки будет записан
оптимальный план назначений (план
закрепления продавцов на торговых точках).
Введем первоначальные значения матрицы
изменяемых ячеек (матрицы ' назначений). Затем в эти ячейки будет записан
оптимальный план назначений (план
закрепления продавцов на торговых точках).

Рядом с матрицей назначений запишем условия
на значения ячеек матрицы назначений.
Установим расположение ячейки, в которой
будет вычисляться значение целевой функции:

Откроем диалоговое окно «Поиск решения». В нем
зададим расположение целевой ячейки (в котором вычисляется значение целевой
функции), вид оптимального
решения (максимальное значение), расположение ячеек, которые будут изменяться при поиске решения (из них
состоит матрица назначений), а также ограничения на изменяемые значения.
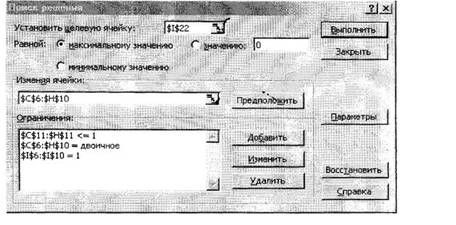
После ввода необходимых данных нажмем кнопку
«Выполнить» диалогового окна. В случае, если решение существует (и все данные
введены верно), появляется сообщение:
 После нажатия кнопки «ОК>> в ячейках матрицы назначений
появляются значения ее оптимальных элементов
(оптимальный план назначений); в ячейке целевой функции вычисляется соответствующее этому плану оптимальное
значение целевой функции. Матрица оптимальных назначений:
После нажатия кнопки «ОК>> в ячейках матрицы назначений
появляются значения ее оптимальных элементов
(оптимальный план назначений); в ячейке целевой функции вычисляется соответствующее этому плану оптимальное
значение целевой функции. Матрица оптимальных назначений:

Таким
образом, суммарный (максимальный) объем продаж на всех торговых точках равен 308 (USD/тыс, шт.), а соответствующий им план
назначений задан таблицей:
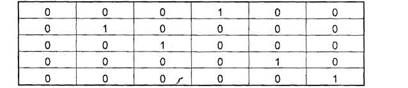
Согласно этому плану назначений, торговая
точка №1 не используется (так как ее использование нерационально).
Следовательно, ее надо продать, закрыть или сдать в аренду (либо, возможно, нанять еще одного продавца).
Задача 1.7 (распределение рекламного бюджета)
Коэффициенты целевой функции (влияние видов рекламы на прибыль)
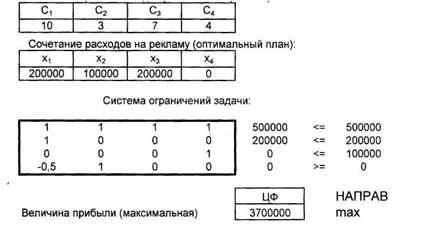
|
Э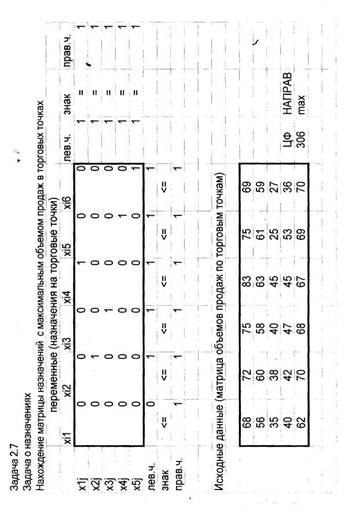
|