Группировка районов по объему оплаты труда

Величина вариации признака в статистической совокупности характеризует степень ее однородности, что имеет большое практическое значение.

Относительным показателем уровня вариации признака является коэффициент вариации v. Он представляет собой отношение среднего квадратического отклонения к средней величине признака и выражается обычно в процентах.

v = σ/хср * 100 %

где σ – средне квадратическое отклонение

хср – средняя величина

Если коэффициент вариации больше 33%, то совокупность неоднородна и ее средняя нетипична.

Расчет средней величины произведем по средней арифметической простой 

Формула для расчета средних величин в зависимости от исходных данных

Хср = ∑Хi/n

Где n – численность совокупность

Хi – варианта или значение признака

Среднее квадратическое отклонение показывает на сколько в среднем колеблется величина признака у единиц исследуемой совокупности и определяется в зависимости от характера.

При расчете используем формулу

σ = √∑(х-хср)²*f/∑f

Расчет показателей вариации по балансовой прибыли необходимо произвести в аналитической таблицы

Расчет показателей вариации по оплате труда необходимо произвести в аналитической таблицы

Рассчитаем коэффициенты вариации для исходных данных и по аналитической таблице.

Средняя по балансовой прибыли = 753337/50 = 15066,74 р.

Средняя по оплате труда = 1163277/50 = 23265,54 р.

По сгруппированным данным

Хср = ∑хi*fi/∑fi = 1063601/50 = 21272.02

Хср = ∑хi*fi/∑fi = 1670950/50 = 33419

Средне квадратическое отклонение по сгруппированным данным

σ балансовая прибыль = √23093717661/50 = √461874353,2 = 21491,26 р.

σ оплата труда = √44106443549/50 = √882128871 = 29700,65 р.

Коэффициент вариации по сгруппированым данным %.

V балансовая прибыль = 21491,26/15066,74 *100 = 142,6

V оплата труда = 29700,65/23265,54 * 100 = 127,66

В обоих расчетах коэффициент вариации значительно больше 33%. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточно типична. В таком случае при практических иследованиях различными статистическими.

Задание 2

Провести 30%  механическую выборку из генеральной совокупности, представленной в таблице 1, по показателю, который является для вашего варианта результативным. С вероятностью 0,95 рассчитать границы изменение средней величины в генеральной совокупности и сравнить с результатом, полученным на основании расчета по выборочной совокупности. Отбор начинать с номера предприятия, который совпадает с номером вашего варианта

Исходные данные

Величина случайной ошибки механического отбора определяется по упрощенной формуле

μ_х = √ σ²/n (1-n/N)

где N – объем генеральной совокупности

n – объем выборки

σ² – генеральная дисперсия

Расчет генеральной дисперсии

Наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения коэффициента доверия t для выборок достаточно большого объема.

Для расчета границ изменения средней характеристики генеральной совокупности по материалам выборки воспользуемся следующими формулами.

Хср = хвыб ±∆

∆ = t μ_х

где хср – средняя генеральной совокупности хвыб – средняя иыборочной совокупности ∆ - придельная ошибка выборки.

μ_х – средняя квадратическая ошибка выборки.

Средняя на одном предприятии по выборочной совокупности равна

Хвыб балансовой прибыли = 753337/50 = 15066,74 р.

Хвыб оплата труда = 1163277/50 = 23265,54 р.

μ_х балансовая прибыль = √219791972/50*0,7 = 1754,16

μ_х оплата труда = √375109109,7/50 *0,7 = 2291,62

∆ балансовая прибыль = 2 * 1754,16 = 3508,33

∆ оплата труда = 2 * 2291,62 = 4583,24

Балансовая прибыль

15066,74-3508,33 < х < 15066,74+3508,33

11558,41< х < 18575,07

Оплата труда

23265,54 - 4583,24 < х < 23265,54 + 4583,24

18682,3 < х < 27848,78

Таким образом, с вероятностью 0,95 можно утверждать, что балансовая прибыль на одном предприятии в генеральной совокупности будет находиться в приделах от 11558,41 р. до 18575,07 руб. а оплата труда от 18682,3 до 27848,78 руб.

Задание 3

По данным своего варианта (табл. 1) рассчитайте:

1) среднегодовой ввод жилых домов;

2) базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста ввода жилых домов;

3) изобразите динамику ввода жилых домов на графике.

Таблица 1

Данные о вводе жилых домов строительной компании «N»

Решение

Абсолютный прирост (∆_i) определяется как разность между двумя уровнями динамического ряда. При сравнении с постоянной базой он равен:

                                                 ∆_i ^б =Y_i – Y₀,                                                    (1)

где ∆_i ^б − абсолютный прирост базисный;

      Y_i − уровень сравниваемого периода;

         Y₀ − уровень базисного периода.

При сравнении с переменной базой абсолютный прирост равен:

                                                 ∆_i  =Y_i – Y_i-1,                                                    (2)

где ∆_i  − абсолютный прирост цепной;

      Y_i-1− уровень непосредственно предшествующего периода.

Темп роста (Т_р) определяется как  отношение двух сравниваемых уровней.

При сравнении с постоянной базой:

                                               Т_р =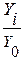*100 %                                                              (3)

 При сравнении с переменной базой:

                                              Т_р =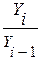*100 %                                                           (4)

Темп прироста показывает на сколько процентов уровень данного периода больше (или меньше) базисного уровня.

                           Т_п =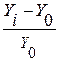*100%   или   Т_п = 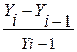*100 %

А также определяет разность между темпом роста (в %) и 100%:

                                           Т_п = Т_р – 100%                                                      (5)

Средний уровень определяется по формуле:

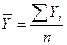                                                                                                                    (6)

Средний абсолютный прирост рассчитывается по формуле:

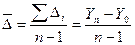                                                                                              (7)

Среднегодовой темп роста определяется по среднегеометрической формуле:

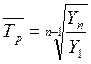                                                                                                       (8)

Среднегодовой темп прироста определяется по формуле:

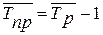                                                                                                  (9)

1) Среднегодовой ввод жилых домов определяем по формуле среднего уровня ряда:

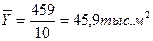
2) Рассчитаем все показатели по ряду динамики, характеризующему величину ввода жилых домов. Данные расчета представим в таблице 2.

Таблица 2

Расчет показателей динамики

Рассчитанные аналитические показатели характеризуют динамику ввода жилых домов за 1987 – 1996 годы. Абсолютный прирост выражает абсолютную скорость роста ввода жилых домов. По сравнению с 1987 годом она составила 17 тыс. м². Темп роста показывает, что ввод жилых домов 1996 г. составляет 148,57 % от уровня базисного года. Темп прироста дает возможность оценить на сколько процентов ввод жилых домов в 1996 г. возрос по сравнению с 1987 годом – на 48,57 %.

Рассчитаем средние показатели, тыс. м²:

а) средний абсолютный прирост:

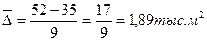
б) среднегодовой темп роста:

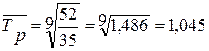
в) среднегодовой темп прироста:

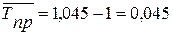
Среднегодовой ввод жилых домов составляет 45,9 тыс. м². В среднем в год ввод жилых домов увеличивался на 4,5 %.

3) Построим диаграмму данного ряда динамики.

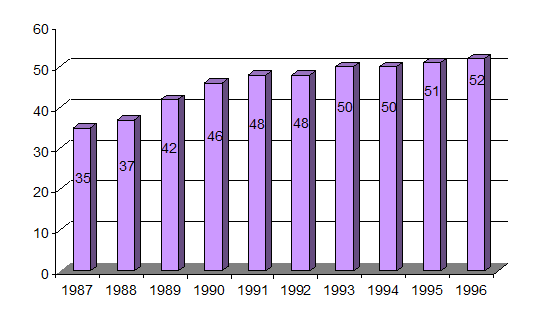
Рис. 1 Динамика ввода жилых домов за 1987 – 1996 годы.

Задание 4

По данным своего варианта (табл. 3) определите:

1) общие индексы:

а) цен;

б) физического объема проданных товаров;

в) товарооборота.

Какую роль в изменении товарооборота сыграли изменения цен и количества проданных товаров?

2) Абсолютную величину изменения расходов населения, происшедших в связи с изменением цен.

Таблица 3

Реализация товаров в магазине

Решение

1) Общий индекс – это особая относительная величина, которая дает количественную и качественную оценку изменения сложных экономических явлений во времени, пространстве или по  сравнению с  планом.

а) Общий индекс цен определяется по формуле:

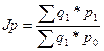                                                                                                  (10)

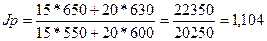
Это свидетельствует о том, что цены на оба товара в среднем выросли на 10,4 %.

б) Общий индекс физического объема товарооборота определяется по формуле:

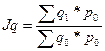                                                                                                  (11)

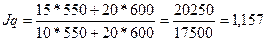
Это свидетельствует о том, что в отчетном периоде было продано больше товаров на 15,7 %, чем в предыдущем периоде.

в) Общий индекс товарооборота определяется по формуле:

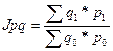                                                                                                (12)

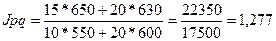
По сравнению с прошедшим периодом в отчетном периоде товарооборот увеличился на 27,7%.

Прирост товарооборота за счет изменения цен составил:

∑р₁q₁ - ∑р₀q₁ = 22350-20250=2100 руб.

Прирост товарооборота за счет изменения количества проданных товаров  составил:

∑р₀q₁ - ∑р₀q₀ = 20250-17500=2750 руб.

Общее изменение товарооборота составило:

∑р₁q₁ - ∑р₀q₀ = 22350-17500=4850 руб.

Можно сделать следующий вывод: в отчетном периоде по сравнению с предыдущим товарооборот увеличился на 2100 руб. за счет увеличения цен на 10,4 % и на 2750 руб. за счет увеличения количества проданной продукции на 15,7%.

2) Абсолютная величина изменения расходов населения, происшедших в связи с изменением цен составит:

∑(р₁ – р₀)*q₁ = (650-550)*15+(630-600)*20 = 2100 руб.

В связи с повышением цен на товары расходы населения увеличились на 2100 рублей.

СПИСОК ЛИТЕРАТУРЫ

1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.

2. Едронова Н. Н. Общая теория статистики. – М.: Финансы и статистика, 2001. – 648 с.

3. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.

4. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2000. – 414 с.

5. Теория статистики / Под редакцией Громыко Г. Л.  – М.: ИНФРА-М, 2002. – 576 с.

6. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.