СОДЕРЖАНИЕ
Задание 1. 2
Задание 2. 9
Задание 3. 12
Задание 4. 17
СПИСОК ЛИТЕРАТУРЫ.. 20
Вариант 1
Задание 1
Для выявления зависимости
между экономическими показателями деятельности фирм провести группировку
показателей 50 аудиторских фирм (табл.1). Группировку провести с равными интервалами,
выделив 4 или 5 групп. Для варианта 1: предприятия 1-50, результативный признак
– выручка от реализации, группировочный признак – численность работников.
Таблица 1
Основные показатели деятельности
аудиторских фирм за период «N»
|
№ п/п
|
Выручка от реализации, р. (у)
|
Численность работников, чел. (х)
|
№ п/п
|
Выручка от реализации, р. (у)
|
Численность работников, чел. (х)
|
|
1
|
112627
|
32
|
26
|
68849
|
14
|
|
2
|
59564
|
8
|
27
|
67580
|
16
|
|
3
|
107062
|
3
|
28
|
15980
|
4
|
|
4
|
0
|
4
|
29
|
11307
|
2
|
|
5
|
57949
|
2
|
30
|
12238
|
3
|
|
6
|
0
|
2
|
31
|
83761
|
15
|
|
7
|
29135
|
3
|
32
|
81235
|
13
|
|
8
|
13256
|
1
|
33
|
85320
|
17
|
|
9
|
10083
|
3
|
34
|
94638
|
35
|
|
10
|
90902
|
8
|
35
|
59187
|
21
|
|
11
|
140000
|
7
|
36
|
61328
|
23
|
|
12
|
12847
|
1
|
37
|
40155
|
10
|
|
13
|
0
|
1
|
38
|
44333
|
11
|
|
14
|
56500
|
5
|
39
|
21500
|
7
|
|
15
|
30841
|
5
|
40
|
39490
|
8
|
|
16
|
35274
|
6
|
41
|
60125
|
9
|
|
17
|
45520
|
2
|
42
|
63100
|
13
|
|
18
|
93578
|
15
|
43
|
72354
|
24
|
|
19
|
53234
|
11
|
44
|
77995
|
27
|
|
20
|
83278
|
43
|
45
|
87486
|
28
|
|
21
|
56119
|
12
|
46
|
98640
|
30
|
|
22
|
47360
|
9
|
47
|
25811
|
7
|
|
23
|
45914
|
2
|
48
|
27415
|
8
|
|
24
|
122502
|
38
|
49
|
32645
|
6
|
|
25
|
142683
|
45
|
50
|
120800
|
36
|
Рассчитать коэффициенты
вариации по группировочному признаку на основании исходных данных и по
аналитической группировке, согласно своему варианту. Объяснить расхождения в
значениях полученных коэффициентов.
Решение
Группировка – это
разделение единиц изучаемого общественного явления по существенным признакам.
В данном примере
представлена аналитическая группировка. Аналитическая группировка – это
исследование взаимосвязи варьирующих признаков в пределах однокачественной
совокупности. Такая
группировка позволяет установить связь между двумя признаками – факторными и
результативными. В нашем примере результативный признак – выручка от
реализации, группировочный признак – численность работников.
Сначала определяем величину
(шаг) интервала группировки. Интервал – это разница между максимальным и
минимальным значением признака в каждой группе.[1]
Величина интервала
определяется по формуле:
d = 
, (1)
где
хmax – максимальное значение
количественного признака;
xmin –
минимальное значение количественного признака;
n – число
намечаемых групп.
Примем
число групп по данному признаку n=4
d = 
Таким
образом, получаем четыре группы:
1
группа: 1 – 12
2
группа: 12 – 23
3
группа: 23 – 34
4
группа: 34 – 45
Принцип
группировки выбираем «включительно».
Далее
проводим группировку. Для этого составим таблицу 2.
Таблица 2
Аналитическая группировка аудиторских
фирм по численности работников
|
Группы фирм по
численности работников, чел.
|
№ фирмы
|
Численность
работников
|
Выручка от
реализации, р.
|
|
1
|
2
|
3
|
4
|
|
1 – 12
|
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
19
21
22
23
28
29
30
37
38
39
40
41
47
48
49
|
8
3
4
2
2
3
1
3
8
7
1
1
5
5
6
2
11
12
9
2
4
2
3
10
11
7
8
9
7
8
6
|
59564
107062
0
57949
0
29135
13256
10083
90902
140000
12847
0
56500
30841
35274
45520
53234
56119
47360
45914
15980
11307
12238
40155
44333
21500
39490
60125
25811
27415
32645
|
|
ИТОГО:
|
31
|
170
|
1 222 559
|
|
12 – 23
|
18
26
27
31
32
33
35
36
42
|
15
14
16
15
13
17
21
23
13
|
93578
68849
67580
83761
81235
85320
59187
61328
63100
|
|
ИТОГО:
|
9
|
147
|
663 938
|
Окончание табл. 2
|
1
|
2
|
3
|
4
|
|
23 – 34
|
1
43
44
45
46
|
32
24
27
28
30
|
112627
72354
77995
87486
98640
|
|
ИТОГО:
|
5
|
141
|
449 102
|
|
34 – 45
|
20
24
25
34
50
|
43
38
45
35
36
|
83278
122502
142683
94638
120800
|
|
ИТОГО:
|
5
|
197
|
563 901
|
|
ВСЕГО:
|
50
|
655
|
2 899 500
|
Для выявления зависимости
выручки от численности работников составим аналитическую таблицу 3.
Таблица 3
Зависимость
выручки от численности
работников
|
Группы фирм по числен-ности работ-ников, чел.
|
Число фирм
|
Численность работников,
чел.
|
Выручка от реализации,
руб.
|
|
Всего по группе
|
В среднем на одну фирму
|
Всего по группе
|
В среднем на одну фирму
|
|
1 – 12
|
31
|
170
|
5,5
|
1222559
|
39437,4
|
|
12 – 23
|
9
|
147
|
16,3
|
663938
|
73770,9
|
|
23 – 34
|
5
|
141
|
28,2
|
449102
|
89820,4
|
|
34 – 45
|
5
|
197
|
39,4
|
563901
|
112780,2
|
Исследовав
экономические показатели 50-ти аудиторских фирм, можно сказать, что выручка от
реализации находится в прямой зависимости от численности работников, то есть с
ростом численности выручка увеличивается.
Величина
вариации признака в статистической совокупности характеризует степень ее
однородности, что имеет большое практическое значение.
Относительным
показателем уровня вариации признака является коэффициент вариации. Он характеризует
относительную меру колеблемости и определяется по формуле:
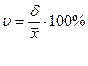(2)
где
δ – среднее квадратическое отклонение;
– средняя величина.
Если
коэффициент вариации больше 33%, то совокупность неоднородна и ее средняя
нетипична.
Расчет
средней величины произведем по средней арифметической простой (при расчете по
исходным данным) и по средней арифметической взвешенной (при расчете по
аналитической таблице).
Средняя
величина по исходным данным определяется по формуле:
,
(3)
где
n – численность совокупности;
х – варианта или значение признака.
Средняя
величина по сгруппированным данным определяется по формуле:
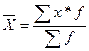(4)
где
f – частота повторения индивидуального
значения признака (его вес).
Среднее
квадратическое отклонение показывает, на сколько в среднем колеблется величина
признака у единиц исследуемой
совокупности и определяется в зависимости от характера исходных данных.
При
расчете по исходным данным используем формулу:
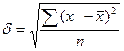(5)
По
сгруппированным данным:
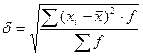(6)
Рассчитаем
показатели вариации для исходных данных.
Для
расчета показателей вариации по исходным данным необходимо составить аналитическую таблицу (табл. 4).
Таблица 4
Расчет
показателей вариации по исходным данным
|
№ п/п
|
Численность работников (х)
|
х-
|
(х-)2
|
№ п/п
|
Численность работников (х)
|
х-
|
(х-)2
|
|
1
|
32
|
18,9
|
357,2
|
26
|
14
|
0,9
|
0,8
|
|
2
|
8
|
-5,1
|
26,0
|
27
|
16
|
2,9
|
8,4
|
|
3
|
3
|
-10,1
|
102,0
|
28
|
4
|
-9,1
|
82,8
|
|
4
|
4
|
-9,1
|
82,8
|
29
|
2
|
-11,1
|
123,2
|
|
5
|
2
|
-11,1
|
123,2
|
30
|
3
|
-10,1
|
102,0
|
|
6
|
2
|
-11,1
|
123,2
|
31
|
15
|
1,9
|
3,6
|
|
7
|
3
|
-10,1
|
102,0
|
32
|
13
|
-0,1
|
0,01
|
|
8
|
1
|
-12,1
|
146,4
|
33
|
17
|
3,9
|
15,2
|
|
9
|
3
|
-10,1
|
102,0
|
34
|
35
|
21,9
|
479,6
|
|
10
|
8
|
-5,1
|
26,0
|
35
|
21
|
7,9
|
62,4
|
|
11
|
7
|
-6,1
|
37,2
|
36
|
23
|
9,9
|
98,0
|
|
12
|
1
|
-12,1
|
146,4
|
37
|
10
|
-3,1
|
9,6
|
|
13
|
1
|
-12,1
|
146,4
|
38
|
11
|
-2,1
|
4,4
|
|
14
|
5
|
-8,1
|
65,6
|
39
|
7
|
-6,1
|
37,2
|
|
15
|
5
|
-8,1
|
65,6
|
40
|
8
|
-5,1
|
26,0
|
|
16
|
6
|
-7,1
|
50,4
|
41
|
9
|
-4,1
|
16,8
|
|
17
|
2
|
-11,1
|
123,2
|
42
|
13
|
-0,1
|
0,01
|
|
18
|
15
|
1,9
|
3,6
|
43
|
24
|
10,9
|
118,8
|
|
19
|
11
|
-2,1
|
4,4
|
44
|
27
|
13,9
|
193,2
|
|
20
|
43
|
29,9
|
894,0
|
45
|
28
|
14,9
|
222,0
|
|
21
|
12
|
-1,1
|
1,2
|
46
|
30
|
16,9
|
285,6
|
|
22
|
9
|
-4,1
|
16,8
|
47
|
7
|
-6,1
|
37,2
|
|
23
|
2
|
-11,1
|
123,2
|
48
|
8
|
-5,1
|
26,0
|
|
24
|
38
|
24,9
|
620,0
|
49
|
6
|
-7,1
|
50,4
|
|
25
|
45
|
31,9
|
1017,6
|
50
|
36
|
22,9
|
524,4
|
|
ИТОГО:
|
655
|
−
|
7033,7
|
Средняя
величина по исходным данным составит:
чел.
Среднее
квадратическое отклонение по исходным данным составит:
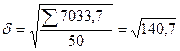=11,8 чел.
Коэффициент
вариации по исходным данным составит:
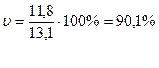
Рассчитаем
показатели вариации для сгруппированных данных.
Для
расчета показателей вариации по сгруппированным данным необходимо
составить аналитическую таблицу (табл. 5).
Таблица 5
Расчет
показателей вариации по сгруппированным данным
|
Группы фирм по численности
|
Число фирм
|
Расчетные показатели
|
|
Середина интервала 
|
|
х-
|
(х-)2f
|
|
1 – 12
|
31
|
6,5
|
201,5
|
-7,5
|
1743,75
|
|
12 – 23
|
9
|
17,5
|
157,5
|
3,5
|
110,25
|
|
23 – 34
|
5
|
28,5
|
142,5
|
14,5
|
1051,25
|
|
34 – 45
|
5
|
39,5
|
197,5
|
25,5
|
3251,25
|
|
ИТОГО:
|
50
|
−
|
699
|
−
|
6156
|
Средняя
величина по сгруппированным данным составит:
чел.
Среднее
квадратическое отклонение по сгруппированным данным составит:
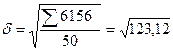=11,1 чел.
Коэффициент
вариации по сгруппированным данным составит:
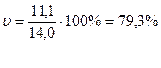
В обоих расчетах коэффициент
вариации значительно больше 33%. Следовательно, рассмотренная совокупность
неоднородна и средняя для нее недостаточно типична.
Задание 2
Провести 30 %
механическую выборку из генеральной совокупности, представленной в таблице 1,
по показателю, который является для Вашего варианта результативным. С
вероятностью 0,95 рассчитать границы изменения средней величины в генеральной
совокупности (по табл.1) и сравнить с результатом, полученным на основании
расчета по выборочной совокупности. Отбор начинать с номера предприятия,
который совпадает с номером Вашего варианта.
Решение
Механическая выборка
представляет собой отбор единиц через равные промежутки (по алфавиту, через
временные промежутки, по пространственному способу и т.д.). При проведении
механического отбора генеральная совокупность разбивается на равные по
численности группы, из которых затем отбирается по одной единице.[2]
Задано 60 предприятий.
Выборка 30 %-ная, значит, в выборочную совокупность должно попасть 18
предприятий. Исходные данные приводятся в таблице 6.
Таблица 6
Исходные
данные выборочной совокупности
|
№ фирмы
|
Выручка от реализации,
руб.
|
№ фирмы
|
Выручка от реализации,
руб.
|
|
1
|
112627
|
28
|
15980
|
|
4
|
0
|
31
|
83761
|
|
7
|
29135
|
34
|
94638
|
|
10
|
90902
|
37
|
40155
|
|
13
|
0
|
40
|
39490
|
|
16
|
35274
|
43
|
72354
|
|
19
|
53234
|
46
|
98640
|
|
22
|
47360
|
49
|
32645
|
|
25
|
142683
|
51
|
19654
|
|
ИТОГО:
|
|
1 008 532
|
Величина
случайной ошибки механического отбора определяется по упрощенной формуле:
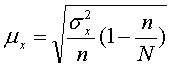(7)
где n – численность выборки, n = 18 фирм;
N – численность генеральной
совокупности, N = 60 фирм.
Средняя выручка в одной
фирме по выборочной совокупности составит:
Для расчета среднего квадратического отклонения составим
таблицу 7.
Таблица 7
Расчет показателей
среднего квадратического отклонения
|
№ фирмы
|
Выручка от реализации,
тыс. руб.
|
х- тыс. руб.
|
(х-)2 тыс.
руб.
|
|
1
|
112,6
|
56,6
|
3203,6
|
|
4
|
0
|
-56
|
3136
|
|
7
|
29,1
|
-26,9
|
676
|
|
10
|
90,9
|
34,9
|
1218
|
|
13
|
0
|
-56
|
3136
|
|
16
|
35,3
|
-20,7
|
428,5
|
|
19
|
53,2
|
-2,8
|
7,8
|
|
22
|
47,4
|
-8,6
|
74
|
|
25
|
142,7
|
86,7
|
7516,9
|
|
28
|
15,9
|
-40,1
|
1608
|
|
31
|
87,8
|
31,8
|
1011,2
|
|
34
|
94,6
|
38,6
|
1490
|
|
37
|
40,1
|
-15,9
|
252,8
|
|
40
|
39,5
|
16,5
|
272,2
|
|
43
|
72,3
|
16,3
|
265,7
|
|
46
|
98,6
|
42,6
|
1814,8
|
|
49
|
32,6
|
23,4
|
547,6
|
|
51
|
19,6
|
36,4
|
1325
|
|
ИТОГО:
|
1 012,2
|
─
|
27 984,1
|
Среднее квадратическое отклонение составит:
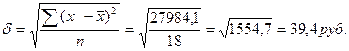
Для
расчета границ изменения средней
характеристики генеральной совокупности по материалам выборки воспользуемся
следующими формулами:
(8)
(9)
где 
─ средняя
генеральной совокупности;
─ средняя выборочной совокупности;
Δх ─ предельная ошибка выборки;
μх ─ средняя
квадратическая ошибка выборки.
Рассчитаем
среднюю квадратическую ошибку выборки по формуле (7):
μх
= 
Значению вероятности 0,95
соответствует значение гарантийного коэффициента, равное 1,96. Тогда предельная
ошибка выборочной средней составит:
Δх =
1,24*1,96 = 2,43
Средняя величина
количественного признака в генеральной совокупности определяется с учетом
предельной ошибки выборочной средней:
= 56±2,43
Пределы, в которых
находится средняя выручка от реализации:
56-2,43≤≤56+2,43
53,57≤≤58,43
Таким образом, с
вероятностью 0,95 можно утверждать, что выручка от реализации в одной фирме в
генеральной совокупности будет находиться в пределах от 53,57 до 58,43 тыс.
рублей.
Задание 3
По данным своего варианта
(табл. 8) рассчитайте:
1) среднегодовой ввод
жилых домов;
2) базисные, цепные и
среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста
ввода жилых домов;
3) изобразите динамику
ввода жилых домов на графике.
Таблица 8
Данные о вводе жилых домов
строительной компании «N»
|
Номер варианта
|
Период, гг.
|
Год
|
Введено жилых домов, тыс. м2 общей
площади
|
|
1
|
1981-1990
|
1981
1982
1983
1984
1985
1986
1987
1988
1989
1990
|
23
26
27
29
30
33
35
37
42
46
|
Решение
1) Средний уровень ряда (
)
характеризует среднюю величину показателя за данный период. Средний уровень
ряда рассчитывается как среднее арифметическое из уровней этого ряда:
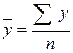(10)
где n-1 – количество изменений за данный период.
Определим
среднегодовой ввод жилых
домов по формуле (10):
2) Абсолютный прирост (
) – это абсолютная разность между последующим и предыдущим
уровнями ряда (цепные) или начальным уровнем ряда (базисные). Цепной абсолютный
прирост характеризует последовательное изменение уровней ряда, а базисный
абсолютный прирост – изменение нарастающим итогом. [3]
Абсолютный прирост
показывает, на сколько абсолютных единиц изменился данный уровень по сравнению:
а) с
предыдущим уровнем при цепном способе:
(11)
где
уi – i-ый уровень ряда,
уi – 1 – i-1-ый уровень ряда.
б) с начальным уровнем при базисном
способе:
(12)
где
уi – i-ый уровень ряда,
у1 – начальный, базисный
уровень ряда.
Темп роста (Тр)
– это соотношение последующего уровня ряда к предыдущему (цепные темпы роста)
или постоянному, принятому за базу сравнения (базисные темпы роста):
Цепные коэффициенты (темпы) роста рассчитываются по
формуле:
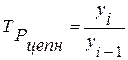(13)
Базисные коэффициенты (темпы) роста рассчитываются по
формуле:
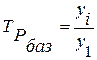, (14)
Темп роста может
выражаться в коэффициентах или в процентах.
Темп прироста показывает,
на сколько процентов изменяется данный уровень по сравнению:
─ с предыдущим
уровнем ряда при цепном способе;
─ с начальным
(базисным) уровнем ряда при базисном способе.
Цепные темпы прироста рассчитываются по формуле:
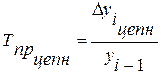(15)
где 
─
цепной абсолютный прирост i-го уровня
ряда,
уi – 1 ─ i-1-ый уровень ряда.
Базисные темпы
прироста рассчитываются по формуле:
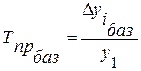, (15)
где
─ базисный абсолютный прирост i-го уровня ряда,
у1 ─ начальный,
базисный уровень ряда.
Темп
прироста обычно выражается в процентах и показывает, на сколько процентов
увеличился (+) или уменьшился (-) текущий уровень по сравнению с предыдущим
(базисным).
Темп
прироста также можно определить исходя из темпа роста:
, (16)
, (17)
где
─
цепной темп роста (в коэффициентах или в процентах).
, (18)
,
(29)
где
- базисный темп роста
(в коэффициентах или в процентах).
Средний
абсолютный прирост (
) определяется по формуле:
= 
(20)
где
Уn – уровень сравниваемого периода;
У0 – уровень базисного периода.
Средний темп роста (
) − это средняя
из темпов роста за данный период, которая показывает, во сколько раз в среднем
(за год, месяц) изменяется явление.[4]
Средний темп роста можно определить исходя из цепных
коэффициентов (темпов) роста:
, (21)
или абсолютных уровней ряда (базисного темпа роста):
, (22)
где 
─
соответствующие цепные темпы роста (yi / yi-1),
─ базисный
темп роста за весь период (yn / y0).
Средний темп прироста (
) характеризует темп прироста в среднем за период и
определяется на основе среднего темпа роста:
,
(23)
, (24)
где
─ средний темп роста (в коэффициентах или в процентах).
Средний темп прироста
показывает, на сколько процентов изменился уровень ряда в среднем за данный
период. Средний темп прироста выражается в коэффициентах или процентах.
Рассчитаем все показатели
динамики, характеризующие величину ввода жилых домов. Данные для расчета
представим в таблице 9.
Таблица 9
Расчет
показателей динамики
|
Год
|
Ввод жилых домов, тыс. м2
|
Абсолютный прирост
|
Темп роста, %
|
Темп прироста, %
|
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
|
1981
|
23
|
─
|
─
|
─
|
100
|
0,0
|
0,0
|
|
1982
|
26
|
3
|
3
|
113,04
|
113,04
|
13,04
|
13,04
|
|
1983
|
27
|
1
|
4
|
103,8
|
117,4
|
3,8
|
17,4
|
|
1984
|
29
|
2
|
6
|
107,4
|
126,1
|
7,4
|
26,1
|
|
1985
|
30
|
1
|
7
|
103,4
|
130,4
|
3,4
|
30,4
|
|
1986
|
33
|
3
|
10
|
110,0
|
143,5
|
10,0
|
43,5
|
|
1987
|
35
|
2
|
12
|
106,1
|
152,2
|
6,1
|
52,2
|
|
1988
|
37
|
2
|
14
|
105,7
|
160,9
|
5,7
|
60,9
|
|
1989
|
42
|
5
|
19
|
113,5
|
182,6
|
13,5
|
82,6
|
|
1990
|
46
|
4
|
23
|
109,5
|
200,0
|
9,5
|
100,0
|
Рассчитаем среднегодовые
показатели:
а) среднегодовой
абсолютный прирост:
= 
тыс. м2
б)
среднегодовой темп
роста:
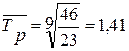, или 141 %
в) среднегодовой темп
прироста:
, или 41 %.
По результатам расчета
показателей динамики можно сделать следующие выводы:
Рассчитанные
аналитические показатели характеризуют динамику ввода жилых домов за 10 лет (с
1981 по 1990 гг.). Абсолютный прирост выражает абсолютную скорость роста ввода
жилых домов. По сравнению с 1981 годом она составила 23 тыс. м2. Темп роста показывает,
что ввод жилых домов 1990 г.
составляет 200 % от уровня базисного года. Темп прироста дает возможность
оценить на сколько процентов ввод жилых домов в 1990
г. возрос по сравнению с 1981 годом – на 100 %.
Среднегодовой ввод жилых домов составляет 32,8 тыс. м2. В среднем за 10 лет
ввод жилых домов составлял 2,6 тыс. м2. Среднегодовой темп роста составил 141 % в
год, причем в среднем в год ввод жилых домов увеличивался на 41 %.
Изобразим динамику ввода жилых домов на
графике. Используем вид графика – столбиковую диаграмму.
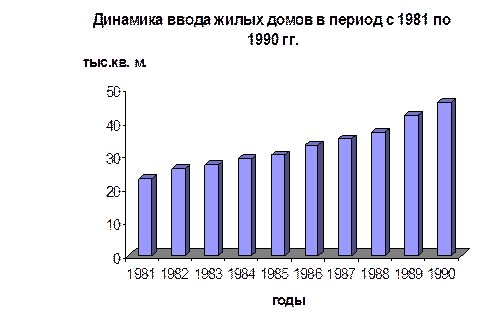
Рис. 1 Динамика ввода жилых домов за
10 лет (1981 – 1990 гг.)
Задание 4
По данным своего варианта
(табл. 10) определите:
1) общие индексы:
а) цен;
б) физического объема
проданных товаров;
в) товарооборота.
Какую роль в изменении
товарооборота сыграли изменения цен и количества проданных товаров?
2) Абсолютную величину
изменения расходов населения, происшедших в связи с изменением цен.
Таблица 10
Реализация товаров в магазине
|
Номер варианта
|
Вид товара
|
Предыдущий период
|
Отчетный период
|
|
Кол-во, шт.
|
Цена за единицу, р.
|
Кол-во, шт.
|
Цена за единицу, р.
|
|
1
|
Утюги
Пылесосы
|
60
30
|
230
600
|
70
80
|
420
1200
|
Решение
1) Индекс – это относительный показатель
сравнения общественных явлений во времени, пространстве или в сопоставлении с
планом.
Общий (сводный) индекс
характеризует изменение по всей совокупности элементов сложного явления.[5]
а) Общий индекс цен
определяется по формуле:
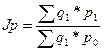(25)
, или 196 %
Цены на утюги и пылесосы
в среднем выросли на 96 %.
б) Общий индекс физического
объема товарооборота определяется по формуле:
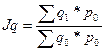(26)
, или 202 %
Количество проданной
продукции было в отчетном периоде больше на 102 %, чем в предыдущем периоде.
в) Общий индекс товарооборота
определяется по формуле:
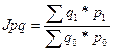(27)
, или 394 %
Прирост товарооборота за
счет изменения цен составил:
∑р1q1 - ∑р0q1 = 125400-64100=61300 тыс. руб.
Прирост товарооборота за
счет изменения количества проданных товаров
составил:
∑р0q1 - ∑р0q0 = 64100-31800=32300 тыс. руб.
Общее изменение
товарооборота составило:
∑р1q1 - ∑р0q0 = 125400-31800=93600 тыс. руб.
Таким образом, в отчетном
периоде по сравнению с предыдущим товарооборот увеличился на 61300 тыс. руб. за
счет увеличения цен на 96 % и на 32300 тыс. руб. за счет увеличения количества
проданной продукции на 102%. Общее изменение товарооборота в отчетном периоде
по сравнению с предыдущим составило 93 600 тыс. рублей.
2) Абсолютная величина
изменения расходов населения, происшедших в связи с изменением цен составит:
∑(р1 – р0)*q1 = (420-230)*70+(1200-600)*80 = 61300 руб.
Таким образом, в связи с
повышением цен на утюги и пылесосы расходы населения увеличились на 61300
рублей.
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория
статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Давыдова Л. А. Теория
статистики в вопросах и ответах: Учебное пособие. – М.: Издательство ТК Велби,
2005. – 160 с.
3. Елисеева И.И., Юзбашев
М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.
4. Ефимова М. Р., Петрова
Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.
5. Савицкая Г. В. Анализ
хозяйственной деятельности предприятия. 2-е изд., испр. и доп. – М.: ИНФРА-М.
2003. − 400 с.
6. Теория статистики /
Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.
[1] Давыдова Л. А. Теория статистики в вопросах и
ответах: Учебное пособие. – М.: Издательство ТК Велби, 2005. – с. 38
[2] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая
теория статистики. – М.: ИНФРА-М. 2002. – с. 161
[3] Теория статистики / Под редакцией Шмойловой Р. А. –
М.: Финансы и статистика, 2002. – с. 189
[4] Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. –
с. 268
[5] Елисеева И.И., Юзбашев М.М. Общая теория статистики.
– М.: Финансы и статистика, 1998. – с. 306