Содержание
8.
Что называется поверхностью равного давления, каковы его форма и уравнение в
покоящейся жидкости, в случае
ускоренного движения сосуда на горизонтальной плоскости и при вращении сосуда
по горизонтальной оси? 3
19.
В чем заключаются условия гидродинамического подобия?. 6
28.
Какие сопротивления называются местными? Как определяются местные потери
напора? От чего зависит коэффициент местного сопротивления? 6
38.
Сформулировать теорему об изменении количества движения и записать на ее основе
расчетное уравнение. 8
Задачи. 9
8. Что называется поверхностью равного давления,
каковы его форма и уравнение в покоящейся жидкости, в случае ускоренного движения сосуда на
горизонтальной плоскости и при вращении сосуда по горизонтальной оси?
Поверхность, во всех точках которой
давление одинаково, называется поверхностью уровня или поверхностью
равного давления. При неравномерном или непрямолинейном движении на частицы
жидкости кроме силы тяжести действуют еще и силы инерции, причем если они
постоянны по времени, то жидкость принимает новое положение равновесия. Такое
равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого
относительного покоя.
В первом примере определим поверхности
уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по
горизонтальному пути с постоянным ускорением a
(рис. 1).
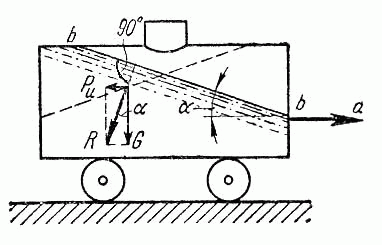
Рис. 1. Движение
цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu,
равная по величине ma. Равнодействующая 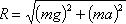 этих
сил направлена к вертикали под углом α, тангенс
которого равен
этих
сил направлена к вертикали под углом α, тангенс
которого равен
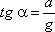
Так как свободная поверхность, как
поверхность равного давления, должна быть нормальна к указанной равнодействующей,
то она в данном случае представит собой уже не горизонтальную плоскость, а
наклонную, составляющую угол α с горизонтом.
Учитывая, что величина этого угла зависит только от ускорений, приходим к
выводу, что положение свободной поверхности не будет зависеть от рода
находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости
также будет плоскостью, наклоненной к горизонту под углом α.
Если бы движение цистерны было не равноускоренным, а равнозамедленным,
направление ускорения изменилось бы на обратное, и наклон свободной поверхности
обратился бы в другую сторону (см. рис.2.6, пунктир).
В качестве второго примера рассмотрим
часто встречающийся в практике случай относительного покоя жидкости во
вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для
разделения жидкостей). В этом случае (рис.2) на любую частицу жидкости при ее
относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu
= mω2r, где r
- расстояние частицы от оси вращения, а ω - угловая
скорость вращения сосуда.
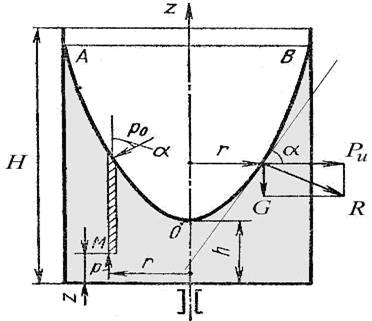
Рис. 2. Вращение
сосуда с жидкостью
Поверхность жидкости также должна быть
нормальна в каждой точке к равнодействующей этих сил R и представит собой
параболоид вращения. Из чертежа находим
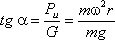
С другой стороны:

где z -
координата рассматриваемой точки. Таким образом, получаем:
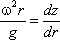
откуда
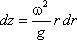
или после интегрирования
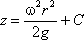
В точке пересечения кривой АОВ с осью
вращения r = 0, z
= h = C, поэтому окончательно будем иметь
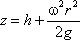
т.е. кривая АОВ является параболой,
а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие
поверхности уровня.
Для определения закона изменения давления
во вращающейся жидкости в функции радиуса и высоты выделим вертикальный
цилиндрический объем жидкости с основанием в виде элементарной горизонтальной
площадки dS (точка М) на произвольном
радиусе r и высоте z
и запишем условие его равновесия в вертикальном направлении. С учетом уравнения
(2.11) будем иметь
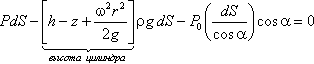
После сокращений получим
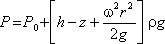
Это значит, что давление возрастает
пропорционально радиусу r и уменьшается
пропорционально высоте z.
19. В чем заключаются условия гидродинамического
подобия?
Необходимыми условиями подобия процессов переноса тепла является
соблюдение гидродинамического подобия
характеризуется равенством критериев Ho, Re, Fr в сходственных
точках подобных потоков, где:
Критерий
Фурье является аналогом критерия гомохронности
Ho при гидродинамическом подобии (учитывает
неустановившийся характер движения в подобных потоках).
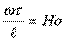
Критерий Рейнольдса
отражает
влияние силы трения на движение жидкости (характеризует отношение инерционных
сил к силам трения в подобных потоках):
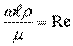
Критерий
Фруда отражает влияние силы тяжести, или собственного веса, на движение
жидкости (является мерой отношения силы инерции к силе тяжести в подобных
потоках):

28. Какие сопротивления называются местными? Как
определяются местные потери напора? От чего зависит коэффициент местного
сопротивления?
Местными сопротивлениями называются участки трубопровода, в
которых происходит резкая деформация потока (к ним относятся, в частности, все
виды арматуры трубопроводов — вентили, задвижки, тройники, колена и т.д.).
Потери напора в местных сопротивлениях 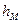 определяются по формуле Вейсбаха
(в долях скоростного напора)
определяются по формуле Вейсбаха
(в долях скоростного напора)
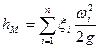
где 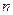 — число местных сопротивлений;
— число местных сопротивлений; 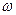 — средняя скорость потока за местным
сопротивлением;
— средняя скорость потока за местным
сопротивлением; 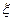 — коэффициент местного сопротивления,
зависящий от его геометрической формы, состояния внутренней поверхности и
— коэффициент местного сопротивления,
зависящий от его геометрической формы, состояния внутренней поверхности и 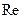 , а
для запорных устройств — от степени их открытия. При развитом турбулентном
движении (
, а
для запорных устройств — от степени их открытия. При развитом турбулентном
движении (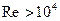 ),
что соответствует квадратичной зоне сопротивления для местных сопротивлений,
),
что соответствует квадратичной зоне сопротивления для местных сопротивлений, 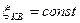 и определяется по справочникам.
и определяется по справочникам.
Потери напора в местных сопротивлениях можно рассчитать по формуле
Дарси-Вейсбаха через эквивалентную длину 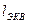 ,
понимая под ней такую длину трубопровода, для которой
,
понимая под ней такую длину трубопровода, для которой 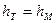 .
.
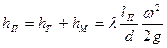
где 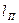 — приведенная длина трубопровода
— приведенная длина трубопровода
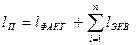
Обычно зона деформации потока в районе местного сопротивления мала
по сравнению с длиной труб. Поэтому в большинстве задач принимается, что потери
напора в местном сопротивлении происходят как бы в одном сечении, а не на
участке, имеющем некоторую длину.
Таким образом, полный перепад давления с учетом местных
сопротивлений и рельефа местности определяется из формулы:
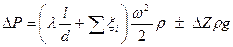 .
.
Коэффициент местного сопротивления зависит от геометрической формы
и внутренней поверхности водопроводов.
38. Сформулировать теорему об изменении количества
движения и записать на ее основе расчетное уравнение
Согласно
теореме об изменении количества движения, приращение количества движения
системы за некоторый промежуток времени равно сумме проекций импульсов сил на
направление движения.
Запишем
расчетные уравнения:
1) Момент
инерции однородного тонкого стержня 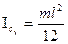
Момент
инерции однородного круглого цилиндра 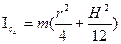
Полого
цилиндра 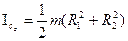 Момент однородного шара
Момент однородного шара 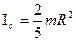
 - это соотношение выражает теорему об изменении момента
количества.
- это соотношение выражает теорему об изменении момента
количества.
2) Движения
материальной точки относительно центра: производная по времени от момента количества
движения материальной точки относительно некоторого неподвижного центра равна
геометрической сумме моментов сил, действующих на точку, относительно того же
центра.
Задачи
Задача 2.
Дано:
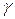 = 7250 Н/м3,
Н = 20 м, D = 200 мм, d = 100 мм.
= 7250 Н/м3,
Н = 20 м, D = 200 мм, d = 100 мм.
Определить:
Давление
пара Р.
Решение:
На
насосный цилиндр бензин давит с силой 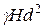 .
.
Давление
в паровом цилиндре р = 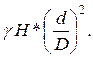
Подставляя
конкретные значения, получаем р = 36,25 кПа или р = 0,37 атм.
Задача 8.
Дано:
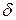 = 910 кг/м3,
Q = 8 л/с,
= 910 кг/м3,
Q = 8 л/с, 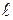 = 8 м, d = 70
мм,
= 8 м, d = 70
мм, 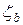 = 8, Sкл = 0,5,
= 8, Sкл = 0,5, 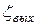 = 1,
= 1,
Rе = 0,2 мм.
Определить:
Давление
Р.
Решение:
Для
эквивалентной шероховатости Rе = (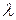 т / 0,11)4 d,
т / 0,11)4 d,
откуда
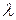 т = 0,0254.
т = 0,0254.
Перепад
давлений вычисляется по формуле
Р –
Ратм = (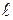 +
+ 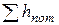 )
) 
Суммарные
потери напора
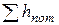 = (
= (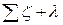 т *
т * 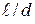 ) *
) * 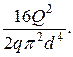
В
результате получаем
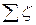 +
+ 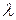 т *
т * 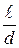 = 12,4
= 12,4
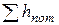 = 2,7
= 2,7
Р –
Ратм = 24 кПа.
Поскольку
атмосферное давление равно 100 кПа, то р = 124 кПа.
Ответ:
Р = 1,24 ат.
Задача 11.
Дано:
Q = 0,285 м3/с, 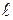 = 276 см, h = 40 см, d = 30
см.
= 276 см, h = 40 см, d = 30
см.
Определить:
Динамическую
вязкость 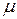 и кинематическую
вязкость
и кинематическую
вязкость 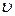 .
.
Решение:
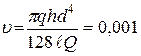 м2/с = 10 см2/с.
м2/с = 10 см2/с.
Динамическую
вязкость 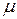 =
= 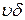 найти невозможно, т.к.
неизвестна плотность жидкости.
найти невозможно, т.к.
неизвестна плотность жидкости.
Задача 23.
Дано:
Q = 25 л/с, 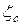 = 12, Нг = 8 м, d = 125
мм, Nе = 3,2 кВт, n = 2500 об/мин.
= 12, Нг = 8 м, d = 125
мм, Nе = 3,2 кВт, n = 2500 об/мин.
Определить:
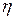 и коэффициент
быстроходности ns.
и коэффициент
быстроходности ns.
Решение:
ns = 3,6 n 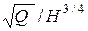 ,
,
где
Н – напор насоса. Напор насоса складывается из геодезической высоты Нг и потери напора в трубе и в целом по системе
h = 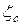
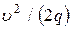
Скорость
течения жидкости 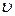 = 4Q / (
= 4Q / ( 2).
2).
Полезная
мощность Nn = Q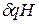 , так что КПД насоса
, так что КПД насоса 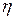 = Nn / Nе.
= Nn / Nе.
Подставляя
конкретные значения, получаем 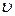 = 2 м/с, h = 2,5
м,
= 2 м/с, h = 2,5
м,
Н =
10,5 м, Nn = 2,6 кВт, 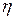 = 0,8, ns = 243.
= 0,8, ns = 243.
Задача 29.
Дано:
Q = 50 л/с, Н = 15 м, 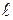 = 25 м, d = 150
мм, n = 90 ход/мин,
= 25 м, d = 150
мм, n = 90 ход/мин, 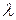 = 0,03,
= 0,03,
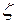 = 20, S:D = 1, d:D =
0,15,
= 20, S:D = 1, d:D =
0,15, 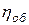 = 0,9,
= 0,9, 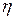 = 0,7.
= 0,7.
Определить:
D, S, мощность N.
Решение:
D = S = 1 м.
Подача
насоса Qн = 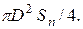
Полезная
мощность насоса Nn = Qn 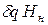 , где Нн – напор насоса.
Полная мощность N = Nn /
, где Нн – напор насоса.
Полная мощность N = Nn / 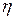 .
.
Напор
насоса складывается из высоты подъёма Н и потерь напора по длине трубопровода с
учётом сопротивления
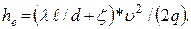
Скорость
течения жидкости найдём по формуле
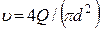
Начиная
вычисления с конца, последовательно получаем 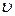 = 2,83 м/с,
= 2,83 м/с,
hе = 10 м, Qн = 1,18 м3/с, N 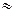 413 кВт.
413 кВт.
Задача 32.
Дано:
D = 25 см, F1 = 5500 Н, Q = 9
л/с, 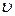 = 1,5 см2/с,
= 1,5 см2/с,
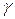 = 14000 Н/м3,
= 14000 Н/м3,
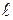 = 20 м,
= 20 м,
d = 5 см, 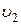 = 2
= 2 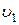 .
.
Определить:
Силу
F2.
Решение:
Из
условия 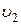 = 2
= 2 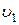 получаем Q1 = 1/3 Q, Q2 = 2/3 Q.
получаем Q1 = 1/3 Q, Q2 = 2/3 Q.
Сила
F предполагает напор 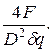
Потери
напора составляют
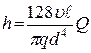
Суммарный
напор в каждой магистрали
Нi
= 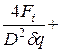
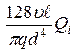
Приравнивая
Н1 и Н2, получаем
F2 = F1 - 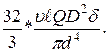
Подставляем
конкретные значения
F2
= 5500 – 460 = 5040 Н.